1. tétel

Halmazok, halmazműveletek, ezek bemutatása természetes számokkal kapcsolatos problémákon.

Alapfogalmak

A halmaz és annak eleme nem definiált matematikai alapfogalmak. (Halmaznak nevezzük az egy meghatározott közös tulajdonsággal rendelkező elemek összességét. Minden elemről egyértelműen eldönthető hogy beletartozik egy halmazba vagy sem.)

Def.: Az olyan halmazt, amelynek egyetlen eleme sincs üres halmaznak nevezzük. Jele:  

Def.: Egyenlő halmazoknak nevezzük az azonos elemeket tartalmazó halmazokat.

Def.: A halmaz részhalmaza B halmaznak, ha A minden eleme eleme B-nek is. Akkor beszélünk valódi részhalmazról, ha A nem üres halmaz, és A nem tartalmazza B minden elemét. Jelölés:

Tétel

Tétel: Egy n elemű véges halmaz részhalmazainak száma 2ⁿ.

1. Bizonyítás: Mivel a halmaz elemeinek száma véges, sorszámozhatjuk az elemeket 1-től n-ig. Ha az i-edik elemet kiválasztjuk a részhalmazba, akkor ehhez az elemhez rendeljünk 1-et, ha nem, akkor 0-t. Így látható, hogy minden részhalmazhoz rendeltünk egy 0 és 1 számjegyekből álló n hosszúságú számsort, illetve minden számsorhoz tartozik egy részhalmaz, vagyis a megfeleltetés kölcsönösen egyértelmű. (Az üres részhalmaznak a csak 0-ból álló, az eredeti halmaznak a csak 1-esből álló számsor felel meg). Az így képzett n hosszúságú számsorok száma 2ⁿ, tehát a részhalmazok száma is ennyi.

2. Bizonyítás: Teljes indukcióval

1. n = 0 (a vizsgált halmaz az üres halmaz) à 1 részhalmaz (az üres halmaz) à 2⁰ = 1 (jó a képlet)

    n = 1 (egyelemű halmaz) => 2 részhalmaz (az üres halmaz és az eredeti) à 2¹ = 2 (jó a képlet)

2. Ha igaz a tétel n-re, akkor igaz (n+1)-re.

    Tekintsük a halmaz egyik elemét: a

à olyan részhalmazok száma, amelyekben nincsen benne a: 2ⁿ (n elemű halmaz részhalmazainak száma)

à olyan részhalmazok száma, amelyekben benne van a: 2ⁿ (a elhagyásával kölcsönösen egyértelmű megfeleltetés létesíthető az előbb leszámolt halmazokkal)

=> összesen 2ⁿ + 2ⁿ  = 2ⁿ⁺¹ részhalmaz van.

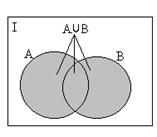
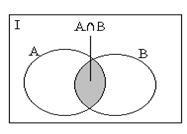
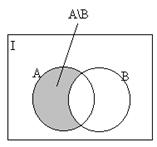
Halmazműveletek

Azt a halmazt, amelyikből válogathatjuk a megfelelő elemeket alaphalmaznak nevezzük. Jelölés: I.

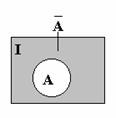
Komplementerképzés

Def.: Egy A halmaz komplementerét egy adott I alaphalmaz felett értelmezhetjük, és mindazon elemek halmaza, amelyek nem tartoznak bele az A halmazba, de az I alaphalmazba igen. Jelölés:

Tulajdonságok:

-

-

-

Unió

Def.:Az A és B halmazok uniója azon elemek halmaza, amelyek A és B halmaz közül legalább az egyiknek elemei. Jelölés:

Tulajdonságok:

- kommutatív:

- asszociatív:

-

-

-

Metszet

Def.:Az A és B halmazok metszete azon elemek halmaza, amelye az A és a B halmaznak egyaránt elemei. Jelölés:

Tulajdonságok:

- kommutatív:

- asszociatív:

-

-

-

Def.: Két halmaz diszjunkt, ha nincs közös elemük, vagyis metszetük az üres halmaz.

- Az unió disztributív a metszetre nézve:

- A metszet disztributív az unióra nézve:

-De Morgan - azonosságok:

1.   ,

2.   .

Különbség

Def.: Egy A és egy B halmaz különbsége azon elemek halmaza, amelyek elemei A-nak, de nem elemei B-nek. Jelölés:

A különbség kifejezése a korábbi halmazműveletekkel:

Tulajdonságok:

- nem kommutatív

- nem asszociatív

-

-

-

-

-

-

Szimmetrikus differencia

Def.: Az A és B halmaz szimmetrikus differenciája azon elemek halmaza, amelyek A és B halmaz közül pontosan az egyiknek elemei. (Tehát minden olyan elem, ami eleme vagy az A halmaznak vagy a B-nek. - kizáró vagy) Jelölés: .

 vagy

Tulajdonságok:

- kommutatív:

- asszociatív:

-  (Biz.:)

-  (Biz.: )

-