A
kör definíciója alapján a P pont akkor és csak akkor van rajta a körön, ha a PK
távolság egyenlő a sugárral. A PK szakasz hosszát fel tudjuk írni a középpont u, v és a P pont x, y koordinátái alapján:
.21. tétel
A kör és a parabola a koordinátasíkon.
Kör
Def.: Azon pontok halmazát a síkban, melyek egy adott ponttól egyenlő távolságra vannak, körnek nevezzük.
Elnevezések, jelölések: Az adott pontot a kör középpontjának (K, O), az egyenlő távolságot a kör sugarának (r) nevezzük.
Tétel: A K(u;v) középpontú, r sugarú kör egyenlete: (x - u)2 + (y - v)2 = r2
Bizonyítás:
A
kör definíciója alapján a P pont akkor és csak akkor van rajta a körön, ha a PK
távolság egyenlő
a sugárral. A PK szakasz hosszát fel tudjuk írni a középpont u, v és a P
pont x, y koordinátái alapján:
.
Mivel mind a két oldal pozitív, ezért négyzetre emelhetünk:
(x - u)2 + (y - v)2 = r2.
A kör bármely pontjának
koordinátái igazzá teszik ezt az egyenletet, más pontok koordinátái viszont
nem, ezért azt mondjuk, hogy ez a kör egyenlete.
Megjegyzés: Azt is meg tudjuk mondani, hogy egy pont hogy helyezkedik el a körhöz képest: be kell helyettesíteni a koordinátáit az egyenletbe, és …
· ha igaz az egyenlet, akkor a pont a körön van,
· ha (x - u)2 + (y - v)2 > r2 akkor a pont a körön kívül van,
· ha (x - u)2 + (y - v)2 < r2 akkor a pont a körön belül van.
A körnek gyakran nem ilyen alakban adják meg az egyenletét.
Ha elvégezzük a négyzetreemelést akkor a következő egyenletet kapjuk:
x2 + y2 - 2ux - 2vy + u2 + v2 - r2 = 0
Ez egy olyan kétismeretlenes másodfokú egyenlet, amiben az x2 és y2 együtthatója egyenlő, és nem tartalmaz xy-os tagot.
Ennek alapján felírható az általános, kétismeretlenes, másodfokú egyenlet:
Ax2
+ Ay2 + Bx + Cy + D = 0, ahol
.
(x - u)2 + (y - v)2 = r2 alakba, ahol r > 0.
Az átalakítás:
Először osztunk a négyzetes tagok együtthatójával:
Kiegészítjük teljes négyzetté:
Rendezzük az egyenletet:
Ez az egyenlet akkor és csak akkor állít elő kört, ha a jobb oldalon levő (r2-nek megfelelő) kifejezés pozitív, tehát B2 + C2 - 4AD > 0.
Ekkor a kör középpontja: K
,
sugara: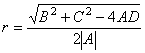 
Parabola
Def.: A parabola azon pontok halmaza, amelyek egy adott egyenestől és az egyenesre nem illeszkedő adott ponttól egyenlő távolságra vannak az adott pont és az adott egyenes által meghatározott síkban.
Elnevezések: Az adott egyenest vezéregyenesnek, az adott pontot fókuszpontnak hívjuk. A fókuszpontnak a vezéregyenestől való távolságát a parabola paraméterének nevezzük, a fókuszpontból a vezéregyenesre állított merőleges egyenest a parabola tengelyének hívjuk. Azt a pontot, ahol a parabola metszi a tengelyt tengelypontnak nevezzük és ez felezi a fókuszpont és a vezéregyenes távolságát.
A parabolának tengelyponti egyenletében a parabola tengelypontja az origó, tengelye pedig valamelyik koordináta tengely. Ez az egyenlet egyértelműen meghatározza a parabola pontjait.
Tétel:
A p paraméterű parabola egyenlete
,
ha a parabola tengelye az y tengely, fókuszpontja az y tengely
pozitív felén van.
Bizonyítás:
Vegyük fel a
vezéregyenest, aminek egyenlete:
A fókuszpont koordinátái:
F (0; 
).
A parabola egy tetszőleges pontja legyen P (x; y), a parabola definíciója szerint: d(P; F) = d(P; v).
A parabola pontjainak a
távolsága a vezéregyenestől: d(P; v) =
A parabola pontjainak távolsága a fókuszponttól:
d(P;
F) =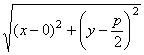 
Tehát:
Mindkét oldal pozitív, ezért nyugodtan négyzetre emelhetünk, a zárójelek felbontása után ezt kapjuk:
Rendezve: x2 = 2py, innen 2p-vel való osztással kapjuk a tételben szereplő egyenletet.
Az is elképzelhető hogy nem így áll a parabolánk:
Ha a parabola tengelye az
y tengely, de fókuszpontja az y tengely negatív felén van, akkor a
parabola egyenlete: 
Ha a parabola tengelye az
x tengely, fókuszpontja az x tengely pozitív felén van, akkor a
parabola egyenlete: 
Ha a parabola tengelye az
x tengely, fókuszpontja az x tengely negatív felén van, akkor a
parabola egyenlete: 
Ha a parabola tengelye
párhuzamos az y tengellyel tengelyű, felfelé nyitott és tengelypontja a T
(u; v) pont, akkor a parabola egyenlete:
Tétel: Minden y tengellyel párhuzamos tengelyű parabolának egyértelműen megfeleltethető egy másodfokú függvény, amelynek ez a parabola a grafikonja, és minden másodfokú függvény grafikonja egy y tengellyel párhuzamos tengelyű parabola.
Tanácsok a feladatok megoldásához
· Amikor két alakzat metszéspontjait keressük, akkor az egyenleteikból álló egyenletrendszert oldjuk meg.
· Amikor érintőt keresünk, akkor egy olyan egyenest keresünk, amely egyenletéből az egyik ismeretlent kifejezve és behelyettesítve a másik egyenletbe a kapott másodfokú egyenlet diszkriminánsa 0, vagyis az egyenletnek csak 1 megoldása van. (Vagyis az egyenletrendszernek csak egy megoldása van, azaz az egyenes csak egy pontban metszi a görbét.)
Érintő keresésénél gyakran segít, ha a parabolához tartozó függvényt lederiválva keressük meg a meredekséget. Ilyenkor figyelni kell, hogy kizárólag olyan parabolákhoz tudunk függvényt rendelni, amelyek lehetnek függvények képei (pl elforgatott parabolához nem)
Alkalmazások
· Sok helyen találkozhatunk parabolákkal a hétköznapi életben. Például elterjedtek a parabolatükrök (paraboloid alakúak), amik a fényt a fókuszpontjukba gyűjtik össze, ilyen tükröket használnak a távcsövekben és az autók fényszórójánál.
· Hasonló elven működnek a parabolaantennák, amik összegyűjtik az elektromágneses jeleket, és a fókuszpontjukban levő vevőkészülékbe koncentrálják.
· A ferdén vagy vízszintesen elhajított test parabolaíven repül légmentes térben, légellenállásnál kis sebesség mellett a pálya torzulása elhanyagolható.