HATODIK RÉSZ - SÍK ÉS TÉR
 

1. A TETRAÉDER

A tetraéder 4 csúcspontú, 4 oldalú és 6 élû geometriai alakzat. (1. ábra) A továbbiakban csak, mint csúcspontokból és élekbõl álló alakzatot fogjuk vizsgálni. Az éleket fogjuk fel úgy, mint két csúcspont által jellemzett új minõséget. Végeredményben tehát csak a csúcspontok az építõelemek. Ekkor úgy írhatnánk le a tetraédert, hogy olyan alakzat, amely 4 pontból áll. Mivel a pontpárokon - az éleken - kívül más minõséget nem vezettünk be, ezért az élek hossza sincs meghatározva, tehát egyformának vehetõk csak. Így már egyértelmû, hogy a 4 pontból (és élekbõl) felépülõ alakzat csak tetraéder lehet.

1. ábra

Egy alakzat annyi dimenziós (nem a szokványos matematikai értelemben), amennyi pontot kell jellemezni az alakzat meghatározásához. Ennek alapján egy pont nulla dimenziós, mivel önmagához képest nem kell információ a meghatározásához. Két pont (egy él) már egy dimenziós, mivel az egyikhez képest a másik különbözik tõle (ugyanis nem azonosak). A tetraéder az elsõ olyan alakzat, ami 3 dimenziós önmagában, de 4 dimenziós egy külsõ nézõpontból szemlélve. A tetraéder magában hordozza a kulcsot, hogyan kell egy alakzathoz úgy hozzárakni új pontokat, hogy minden egyes új pont által az alakzat dimenzió száma eggyel növekedjen. Ellentétben pédául a négyzettel, amely szintén 4 pontból áll, mégsem 3D alakzat. De a tetraéder titka már a háromszögnél is felfedezhetõ. A tetraéder a (teremtési) hierarchia kialakításának, megértésének a geometriája.
A tetraéder rendeltetését tekintve szemléletesebben meghatározható, ha élekkel definiáljuk.: Olyan alakzat, amelyet két különbözõ irányél határoz meg. Tehát egy olyan alakzat, amelyben legalább két különbözõ él van. Természetesen az élek végpontjai definíciószerûen páronként új éleket határoznak meg. Ugyanakkor bármely két él sem metszheti egymást, mivel maga a metszéspont egy új minõség lenne. Ha ehhez hozzávesszük azt, hogy az élek azonos hosszúságúak, akkor egyértelmûen tetraédert kapunk. Lehet ugyan próbálkozni sík alakzat létrehozásával, de a nem metszõ, azonos hosszúságú élek, mint kritérium elõbb-utóbb akadályokat jelentenek.
A két irányél egy új minõséget jelent: a síkot (definíciószerûen). A mindennapi élet során is ezt tapasztaljuk bármely területen; ha van két különbözõ irányunk, akkor azok egy síkot jelentenek. Hasonlóan a matematika világában is két különbözõ vektor az általuk meghatározott síkot kifeszíti, azaz a síkjukba esõ bármely vektor elõáll lineáris kombinációjuk által.
Ha egy speciális nézõpontból nézzük a tetraédert, akkor gyönyörûen látszik, hogy valóban két irányélet határoz meg (2. ábra), amelyek ráadásul merõlegesek és természetesen a vártnak megfelelõen kitérõek is. Ez azonban egy érdekes dolgot vet fel.: A tetraéder, ami a síkot, mint új minõséget bevezeti 3 dimenziós alakzat, míg a sík 2 dimenziós - legalábbis idáig mindenki ezt állította. A megoldás kézenfekvõ: vagy a sík 3 dimenziós vagy pedig egy adott dimenzió számú dolgot csak egy magasabb dimenzióban lehet meghatározni.

2. ábra

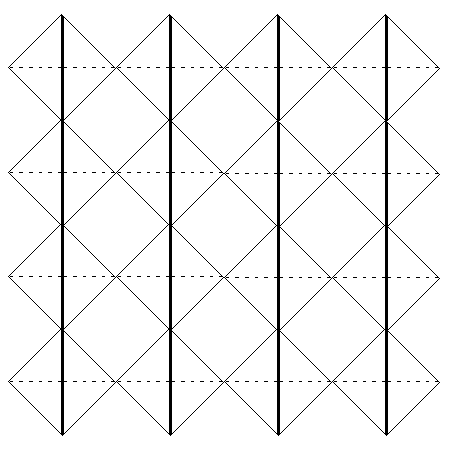
3. ábra

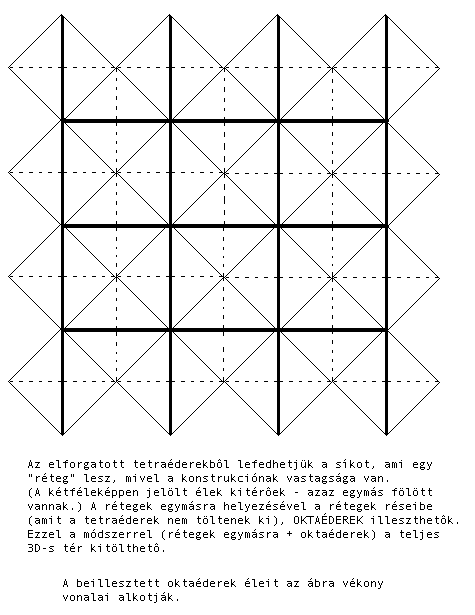
4. ábra

Ha most a feltételezésünkhöz híven elkezdünk építkezni a tetraéderbõl, hogy a síknak legalább egy részletét megkapjuk, érdekes dolgok jelennek meg.: Vegyünk tehát a 2. ábrának megfelelõ felállásban tetraédereket és rakjuk egymás mellé, fölé és alá, hogy egy nagyobb (pl.: téglalap alakú) elrendezõdést kapjunk (3. ábra). A vastagok azok az irányélek, amelyek felül vannak. A vékonyak azok az irányélek, amelyek alul vannak. A többi összekötõ él szaggatott. Ekkor párhuzamos vonalakat kapunk alul és felül. Természetesen bármely alsó és hozzá egy tetszõleges felsõ vonal merõleges. A szaggatott élek biztosítják az átjárást az alsó és felsõ szintek között. De ugyanakkor ez az alakzat még nagyon "üreges". Ezt megszüntethetjük úgy, hogy a hézagokba szintén egy-egy tetraédert helyezünk megfelelõen elforgatva. Ekkor a 4. ábrának megfelelõ elrendezõdést kapjuk meg. Meglepõ módon (vagy tán mégse), egy-egy négyzethálót kapunk a vastag és vékony élek által alul és felül, amely két szint között továbbra is a szaggatott élek az átvezetõ élek.
Tehát végeredményben két négyzethálót - így két síkot is kaptunk volna?! Vagy inkább ez továbbra is egy sík, csak KÉT oldala van? Merthogy ez a sík nem egy oldalú, az biztos. Elképzelhetõ, hogy önmagában egyoldalú sík nem is létezhet. A két oldal biztosítja egymás létezését. A matematikát sem zavarhatja ez, mivel a két oldalt egy él választja el egymástól, azaz a sík vastagsága 2 pontnyi, ami továbbra is semmi (nulla vastagságú).
Tüzetes szemlélõk talán azt is észreveszik, hogy mindkét oldalon a négyzetháló négyzeteibe egy-egy piramis fordítható. Ha az így megspékelt síkokból párat egymásra helyezünk, akkor a piramisok belül oktaéderekké illeszkednek. Az oktaéderek szerepe a 3 irány meghatározása (elöl-hátul, jobbra-balra, fel-le), így azok a teret, mint új minõséget vezetik be. Így viszont egy tömör téglatestet kapunk, mint az euklidészi tér egy részét. Végeredményben a lényeg az, hogy a tér és a síkok fizikailag egy szerkezetet alkotnak, egymástól elválaszthatatlanul, egy helyen.
Még annyit tennék hozzá zárszóként, hogy az oktaéder a maga 6 csúcspontjával egy 5 dimenziós alakzat, amely kívülrõl (vagy belülrõl a középpontból) nézve 6 dimenziós.
 

2. KVATERNIÓK

Nemrégiben felhívta George Kisfaludy a figyelmemet arra, hogy a kvaterniók összefüggésben lehet a tetraéderrel, és hogy a kvaterniók valós része lenne maga az idõ. Utána gondolva a dolognak a következõk derültek ki a számomra.:
Az általunk használt algebra többnyire a valós és komplex számok testén alapszik. A valós számok testében a változók számok - skalárok. A komplex számok testében a vátozók már egy számpár: valós és képzetes számok. Itt továbbra is érvényesek azok az axiómák és tételek, amelyek a valós számokra is igazak voltak. Ezután történik egy furcsa dolog. A várttól eltérõen a következõ, nagyobb, az elõzõ számtesteket magába foglaló új matematikai struktúra nem számhármasokból épül fel, hanem számnégyesekbõl: egy valós és három képzetes összetevõbõl. Továbbá ez már nem test, hanem ferdetest, azaz a szorzás már nem felcserélhetõ: a*b már nem biztos, hogy egyenlõ b*a -val. De a legmeglepõbb az, hogy ezen ferdetest - a kvaterniók - felett már bizonyítottan nem létezik olyan matematikai struktúra, amely teljesíti a valós számok axiómarendszerét.
Tehát van 1D, 2D és 4D algebránk és nincs több. A korábbi - tetraéderes gondolatmenetben beszéltünk élekrõl, síkokról és térrõl. A síkok és a tér is élekbõl épül fel. Viszont az élek kavalkádja új minõségek megszületéséhez vezet, amelyek önmagukban nem létezhetnek az élek nélkül. Amolyan látszat létezõk emiatt, csak az él a valós, ami önmagában 1D-t jelent. A tér, amely önmagában 3D lehetne a sík keletkezésénél elmondott okok alapján, szintén csak egy magasabb dimenzióban határozható meg - hozható létre. Szüksége van egy magasabb (4D) beágyazó dimenzióra, amely azt élteti.
 

3. AZ ÉLET

És most valami merész dolog fog következni! Az idõs embereket szokták másképp éltes embereknek is hívni. Ha vesszük a két jelzõ szótövét az idõt és az életet - élt, akkor azt kapjuk, hogy a szóbeszédben az idõ és az él egy fogalom. Tegyük most mi is ezt. Cseréljük fel az élt az idõre.
Így új megvilágításban láthatjuk a geometriát, mint idõ - élet struktúrát. Az egység szakadása után, miután a megnyilvánult elvált a megnyilvánulatlantól, persze nem véglegesen - egymásba rezegve léteznek - alakult ki az idõ, az élet. Leginkább a jin-jang ábra érzékelteti legjobban a megnyivánult - megnyilvánulatlan rezgésébõl kialakuló élet - idõ szövedéket, amelyben a Pontok jelképezik az eredeti egységet, most már részeire hullva, és köztük az él, illetve az idõ az, ami dinamikát, mozgást, életet hoz a rendszerbe, és életszövedékké alakítja ki a részek pontjait. Így hozza létre (és az ellenállásán kereszül tartja fenn) az idõ a teremtett világot. Az ellenállás alatt azt értjük, hogy az idõ az általa képviselt dinamikája révén nem engedi a részek újra egyesülését az isteni egységbe, az EGYbe.
 

4. A TEREMTŐ

Most már csak arról nem szóltunk, Aki mindezt véghez vitte. Õ a TEREMTŐ (Akirõl, mint TŐrõl fakad a TÉRem?). Ő a legparányibb az egész világban - szinte semmi. Túl van Ő mindenen - az ellentétek világán - ahogy azt mondani szokták. Álmával teremti a világot - amíg álmodja (szubjektíven). Ő csak egy nézõpont és attól függõen, hogy honnan nézi az élet-idõ szövedékét, mindig mást és mást lát. Sõt, úgy tûnhet neki, mintha minden mozogna. Ő az isteni harmadik. Így kerek a kép - a szent háromságban.
A térben Ő maga a 4. dimenzió. Ő az, Aki életet hoz az anyagba általunk. Mi emberek is 4 dimenziósak vagyunk. Ha elveszünk magunkból mindent, ami anyagi, ami nem a mienk, akkor megmarad Ő, a maga sugárzó gyöngyörûségében. A beavatottak már tudják és tudatosan élik át magukat Őbenne és sugározzák ki szeretetét. A SZERetet, az univerzális SZER, az életelixír, amibõl annál többet kapsz, minél többet sugárzol ki. (Úgy, mint a jó csatorna: minél nagyobb a keresztmetszete, annál több megy át rajta. Annál több-ben részesül maga csatorna is, és ráadásul a forrás is benne van...) De jó volna beavatottnak lenni...!
Utána néztünk, hogy a SZER szótóbõl milyen szavaink vannak a magyar nyelvben. Meglepõen teljes szókincset alkottak. Az élet minden területével kapcsoltban volt belõlük egy-két fontos alapszó. Lehetne olyan kommunikációt kialakítani, amely szinte csak ezekre a szavakra alapul. Ízelítõnek felsorolunk néhány általunk érdekesnek talált szót (nem akarjuk elvenni a nyelvészek kenyerét).: szer, szeráf, szeráj, szerda, szerel, szerelem, szerencse, szerény, szerep, szerepel, szeret, szeretkezik, szerez, szerint, szerinte, szerkeszt, szerkezet, szerszám, szertár, szerte, szertelen, szerv, szerves, szervez, szervezet, szerzet, szerzõ, szerzõdés.

Készült: 1995.08.

Vissza a tartalomhoz

Vissza az altartalomjegyzékhez