A BINDU FORGÁSA

"A Bindu egy körbejáró okoskodás."

1. FORGÓ MANDUK

   Egy Bindu két Manduból áll. Egy Mandu forgása önmagában nem értelmezhető, csak egy másik Manduhoz képest. A Mandu tehát egymagában megnyilvánulatlan, nem forog és csak egyféle van belőle (1. ábra). Ő az Első Egyetlen, aki időtlen és mozdulatlan, ezért örök és abszolút. Ebből következik, hogy a forgás (az időbeliség, a dinamizmus) a Bindu jellemzője, a két egymás számára megnyilvánuló, létező Mandué. Így lesz a Bindu az idő forrása, minden teremtés kezdete (2. ábra).

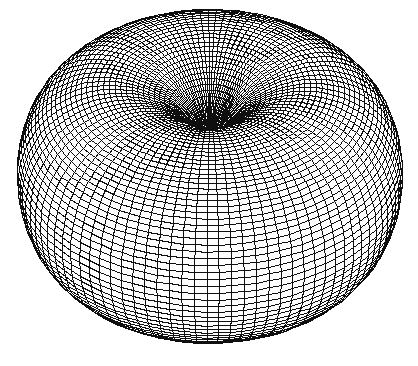
   Forgassunk körbe egy Mandut. Ehhez tekintsük a felületét térbeli kiterjedésű, tehát sok pontból álló halmaznak, aminek geometriai szerkezete van (tórusz). Meg kell határoznunk a tóruszon áthaladó forgástengelyt, ami alapvetően kétféle lehet. Az első képen a tengely csak egy pontban metszi a Mandut, középen, az anomáliás pontban, ahol a felület 180 fokot fordul (3. ábra). Ezt nevezzük a továbbiakban origónak. Megfigyelhető, hogy a felület pontjai az időbeli körbeforgatáskor mindvégig rajta maradnak a felületen, azt el nem hagyják. A felület tehát minden pillanatban fedi önmagát.

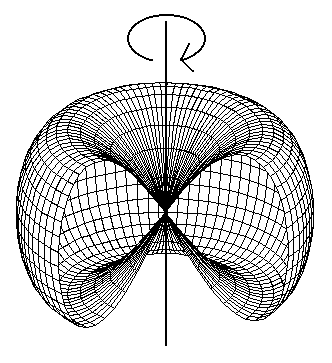
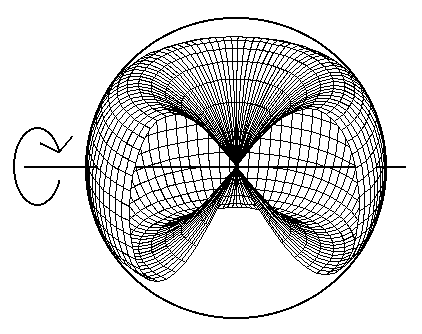
   A másik képen a tengely több pontban, esetünkben három helyen metszi a felületet (4. ábra). Középen és a felület két tetszőleges, de az origótól legtávolabbi pontján. Ekkor a Mandut körbeforgatva az azon lévő pontok kilépnek a felületből és a Mandu köré írható gömb belsejében írnak le körpályát. Egy teljes körbeforgatáskor a felület különböző pontjai a kiindulási felületet eltérően metszik. A metszések számát nevezzük lefedési számnak vagy pontsűrűségnek a továbbiakban. A pontsűrűség definíciója tehát: egy ponton adott időszakaszon belül hány pont halad át, metszve azt. Az időszakasz célszerűen egy fordulat a rendszer számára.
   A Mandu felületén lévő azon pontok, amik az origótól a legmesszebb vannak, egy kört alkotnak. Ennek pontjai egyszer metszik a kiindulási felületet, ezért az általuk lefedett gömb felszínének minden pontja kettős pontsűrűségű. Az origó mindvégig önmagát fedi. Úgy is mondhatjuk, végtelen a pontsűrűsége. Minden olyan pont a Mandu felületén, aminek távolsága az origótól nagyobb nullánál és kisebb a maximálisnál, háromszor metszi a felületet, ezért négyszeres pontsűrűségű.
   A Mandu fél fordulat megtétele után fedi le újra önmagát, ekkor a pontjai által bejárt gömb pontsűrűsége a következő: a gömb felszíne egyszeres, a belseje kétszeres, az origója továbbra is végtelen (mert végtelen/2=végtelen) (5. ábra). Mindebből megállapítható, hogy a forgástengely és a felület metszéspontjai a forgatás során eltérő tulajdonságúak lesznek.

   A forgástengely másféleképpen is átvezethető még a Mandun, de azokkal az extrém esetekkel majd egy külön írásban foglalkozunk. Sokkal fontosabb kérdés most, hogy miért forog az időforrás?
   Az idő dinamikus valami. Dinamizmust mindenféle mozgás nélkül elképzelni pedig nem lehet. Van helyváltoztató (lineáris) és helyzetváltoztató (ciklikus) mozgás. A megnyilvánuláskor a kettő együtt, egyszerre kezd létezni és kölcsönös függőségben vannak. Amelyik forrás állni látszik a többi forrás számára, az nem is forog, erről volt már szó a korábbi írásokban. A Mandu belső, geometriai szerkezete (tórusz) önmagában egy körüljárási útvonalat ad az időnek, zárt ciklusban. Ezen ismétlődés révén lesz önfenntartó a belvilága. Az önfenntartó tulajdonságának kifelé, más források számára történő megnyilvánulását nevezzük relatív forgásnak. Ebből származtatjuk később az abszolút forgást a következő fejezetben.
   A forgás tehát, mint minden mozgás időben történik (csak abban értelmezhető). A Mandu által bejárt tömör gömb ezért szintén időben létezik. Ez az időgömb, az eseményhorizont, aminek keltése fél fordulatot igényel a forrásától. A Mandu spinje így kettő. Mivel a gömb felszínének idősűrűsége csak fele a belsejének, a tulajdonságai is mások lesznek (egyetlen eszményi pillanatra) ha interakcióba lép egy másik időforrással.
   Két Mandu egymáshoz képest eltérően foroghat. Lehet mindkettő balos, mindkettő jobbos vagy egymással ellentétesek. Találkozáskor annak a valószínűsége, hogy nem csupán a forgásirányuk azonos, de a forgástengelyük is, gyakorlatilag nulla. A forgás sebességéről most még csak annyit mondjunk, hogy szintén tetszőleges lehet (valamely véges érték). Megállapítható tehát, hogy két Mandunak egymáshoz képest három eltérő tulajdonsága figyelhető meg: forgásirány (kétféle), forgásszög (kvázi végtelenféle), forgási sebesség (kvázi végtelenféle).

2. AZ ESEMÉNYHORIZONT

   Mivel két Pont a semmiben egymástól semekkora távolságban létezik, ezért ábrázolhatjuk őket geometriailag egymásba ágyazva, közös origóval. Minden olyan esetben, amikor a három fenti paraméterük nem egyezik meg, tehát nem fedik egymást, az időben figyelve őket két Mandut fogunk látni. Felmerül a kérdés, hogy a két tórusz hogyan forog egymáshoz képest?
   Az egyik forog a másik körül, a másik forog az egyik körül. Mivel mindkettő Pont, térbeli kiterjedés nélkül, bármelyiket tekinthetjük alapnak, amihez a másik mozgását viszonyítjuk. A viszonyítási alapot akár cserélgethetjük is dinamikusan, mivel fél fordulatonként fedik egymást. Azt mondhatjuk tehát, hogy hol az egyik fordul körbe a másik körül, hol a másik az egyik körül. Ez nem fog különbözni attól, ha csak az egyik forog a másik körül a forgás szubjektív jellege miatt. Így a teljes körbefordulás két önálló részre bomlik, s ezzel két egymásba ágyazott eseményhorizontot kapunk.
   Ennek köszönhető az eseményhorizont diszkrét, kvantált jellege. Az időhullámtér belül folytonosnak mutatkozik, mégis megfigyelhető benne periodikusság. A létezés szerkezetének leírására ezért alkalmasak a kevert (diszkrét és folytonos felépítésű) modellek. Az ábrákon ezt kék és sárga színekkel jelöltem (6.-7. ábrák). Az emanáció kétféleképp modellezhető geometriailag: állóVÍZként és folyóVÍZként. Ha a két forrást egy helyre képezzük le, állóVIZet kapunk. Ha kölcsönösen taszítva egymást szétszaladnak, időszálat húzva maguk után, folyóVÍZ az eredmény.

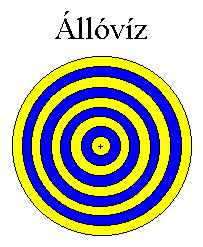
   Az eseményhorizont alapfrekvenciájának hullámhossza (1 sárga + 1 kék zóna) tehát arányos a Mandu egy teljes körbefordulásával. Mivel semmi sincs, ami a forrás abszolút forgási sebességét (továbbiakban AR) megváltoztathatná, ezért minden Mandu forgása csak rá jellemző, egyedi etalonként nyilvánul meg a szemlélők (többi Mandu) számára. A minden létezőt alkotó tíz okforrás, tíz Mandu tehát tíz alapetalont szolgáltat egymás számára. Mivel azonban a források a létezési interakciók során lineárisan mozogni látszanak egymáshoz képest (relatív sebességgel: RV), valamint önmagukhoz képest is mozognak (abszolút sebességgel: AV) a forgás sebessége is relatív módon észlelődik (továbbiakban RR).

3. MOZGÁS ÉS FORGÁS

   Lássuk a mozgási és forgási sebességek közti összefüggéseket. Legyen két forrásunk kezdetben: a és b. A megértéshez elolvasásra ajánlom a 2001-es év anyagai közt "A megnyilvánulás folyamata" című írást, valamint a 2002-es év anyagai közt a "Kezdeti megnyilvánulások" és "Az őskáosz" című írásokat.
Az állóVÍZ modell esetén az a számára bAR=bRR=b1, bAV=bRV=0. A b számára aAR=aRR=a1, aAV=aRV=0. A b1 és a1 nem egyenlő nagyságú és lehet azonos vagy ellentétes irányú.
   A folyóVÍZ modell esetén az a számára bAR=b1, bRR=0, bAV=1, bRV=0. A b számára aAR=a1, aRR=0, aAV=1, aRV=0. Tehát az aRR=bRR, az aAV=bAV és aRV=bRV. A két forrásnak az AR-je természetesen továbbra is különböző (feltételezzük, hogy ez nem változhat), mint az állóVÍZ modellnél, de az RR-jük nulla, vagyis kölcsönösen állni látják a másikat. Az AV-hez tartozó mozgásirányuk ellentétes, az RV-jük pedig azért marad nulla, mert egymás eseményhorizontján tartózkodnak, állni látszanak a másiknak. A relatív sebesség akkor válik értelmezhetővé, ha egy harmadik időforrás csatlakozik a rendszerhez. Két eltérően mozgó forrás esetén már van értelme különbséget tenni a sebességek között. Lehet értelmezni, a c forrás számára hogyan (merre és mennyivel) mozog az a és b forrás. A témát részletesen lásd: az "Időegyenes és időkör" című írásban.
   Mindebből látható, hogy a két modell közti különbség a leképzés céljában van, hogy mit akarok kiemelni a vizsgálódáshoz. Az egyszerűbb állóVÍZ modell hiányossága, hogy nem látszik benne a jelen által húzott primer időszál. Az RR és RV közti összefüggést az alábbi grafikon szemlélteti (8. ábra).

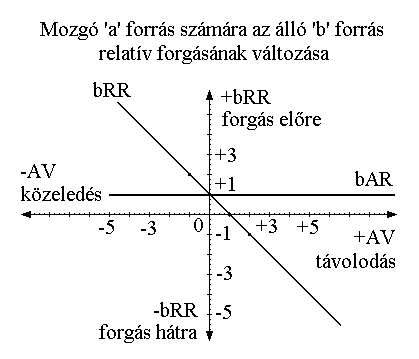
4. KÖLCSÖNHATÁSOK

   További következménye az emanációs gömb pontsűrűségének, hogy magyarázatot ad a taszítási jelenségre. Az eseményhorizont felszíne egyszeres sűrűségű, a belseje kétszeres, az origója pedig végtelen.
   Tudjuk korábbi topológiai kutatásainkból, hogy az egyoldalú felületek egy pont vastagságúak, a kétoldalúak két pont vastagságúak. Az egyoldalú felület topológiai szempontból nem átjárható, nem lehet átlyukasztani (erővel átmenni a túloldalára), mert a másik oldala is ez az oldal, tehát nincs valódi másik oldala. Fizikailag viszont átjárható, mert ha ezen az oldalán vagyok, akkor már a másik oldalán is vagyok, ami pontnyi felület esetén egy helyre esik. A kétoldalú felület átlyukasztható, mert van valódi másik oldala. Fizikailag is átjárható, hisz két pont vastagságú, vagyis olyan az egész, mintha két egyoldalú felülettel találkoznánk egymás után.
   Ebből következik, hogy ha egy eseményhorizont érintkezik egy másik eseményhorizonttal, zavartalanul áthaladnak egymáson, anélkül, hogy bármilyen hatással lennének a másikra. A hullámfrontok kölcsönösen levegőnek nézik egymást, azaz nem észlelik a másikat, nem léteznek egymás számára.
   Ha egy (Bindu által kibocsátott) eseményhorizont egy időforrással (Manduval vagy Binduval) érintkezik, taszítani, sodorni kezdi azt a saját (E=1) sebességével érintőirányban. Az ok: a Mandu létezése a többi forrás hullámterében realizálódik, mindig ott, ahol a hullámtér éppen meghatározza. Tehát nem valódi, erőkifejtés útján megvalósuló taszításról és sodrásról van szó, mint azt sokan képzelik, hanem szubjektív sajátidőbeli pozíció meghatározottságról. Ezért változik a források sebessége a hullámmal találkozva azonnal, ugrásszerűen, mindenféle gyorsulás vagy lassulás nélkül (AV=0-ról azonnal 1-re vagy még nagyobbra). A Pontok ugye transzcendensek, ezért nincs tömegtehetetlenségük.
Harmadik lehetőségként ha két Pontot próbálunk ütköztetni, azok is áthatolnak egymáson, lásd az "Időforrások ütköztetése" című írást a 2002-es év anyagai közt. Összességében tehát elmondhatjuk, hogy a teremtésben minden átjárható, semmi sincs teljesen elszeparálva a környezetétől.
   A rugalmasság, ellenállás és áthatolhatóság jelensége, ami több forrás interakciójának eredménye, a források komplex hullámterekbe rohanásakor, a sodrási vektorok összegzéséből következik. Ennek fontos következménye a lökdösődés, a forráspontok állandó modulációja, szitálása a hullámtérben, ami az információ keletkezésének és megőrződésének fizikai alapja a továbbiakban.

5. ÉSZREVÉTELEK

   Az eddig felsoroltaknak számos messzeható következménye van, ezekből sorolunk itt fel egy csokorra valót a teljesség igénye nélkül.
- A Bindu (tardion) hullámtere belül tehát kettős idősűrűségű. Ebből következik az a logikus észrevétel, hogy a tachion kúp alakú hullámtere belül nem két, hanem négyszeres pontsűrűségű lesz, ráadásul negatív idő, mert befelé vonz, szív a fordított vektorok miatt, míg a tardion csak kifelé taszít minden irányban.
- A Binduban körbeforgolódó két Mandu abszolút forgási sebessége egymáshoz viszonyítva valamely véges érték lehet (aAR és bAR), tehát nem nulla és nem végtelen. Ebből következik, hogy a felfúvódó eseményhorizont réteg nem szabályos gömb alakú, hanem csavarodó spirálgömb lesz. Ugyanolyan szerkezetű, mint a körpályán haladó tachion hullámtere, csak jóval sűrűbb. Ennek oldalirányú, félresodró komponense azonban nagyon kicsi, ezért a hatása is csak érintőleges (de nem nulla) az elért forrásokra. A pontosabb modellezésnél ezt mindenképpen figyelembe kell majd vennünk a későbbiekben.
- Akkor viszont a térforrás spirálgömbi hullámterében két forgási komponens figyelhető meg. Egyrészt a tachion forrása önmaga körül csavarodik száguldás közben, másrészt kering a ciklikus rendszerben. A témát részletesen lásd: a "Dimenziógeometria" című írásban. Ez további fontos következményekkel jár a hullámtér szerkezetére és tulajdonságaira nézve, mert nem mindegy, hogy egy jobbos Atya forrás balra kering vagy jobbra kering (egy balos Anya forrásnál szintén). Jelenlegi tudásunk szerint a mi téridőnk a jobbos Atya jobbra keringő térforrásából ered. A mi antiterünk, amivel szimbiózisban élünk, de szigorúan elszeparálódva tőle, a jobbos Atya balra keringő térforrásából ered. A balos Anya téri és antitéri rendszerei mindkettőtől különbözni fognak, nem is élünk velük szimbiózisban, bár tudunk róluk.
- További következmény, hogy az eltérő abszolút forgású Mandukból eredő időszál rendszerek is eltérő belső szerkezetűek lesznek és nem tudni, egyáltalán összekapcsolhatók-e egymással? A téri és antitéri rendszerek ha egy okforrásból erednek, összekapcsolhatók időszálasan, mert a szálon nem megy át a forgási (azaz keringési!) komponens hatása a két végpont között. Ezt részletesebben lásd: "Az időszálak belső szerkezete" című írásban.
   A forgás jelenségével kapcsolatos kutatások tehát még nem zárultak le, maradt felfedeznivalónk holnapra is.

Készült: 2003.06.-2004.04.

Következő írás

Vissza a tartalomhoz