A VÉGTELEN ÉS A PÁRHUZAMOS EGYENESEK

   Az akasha matematikai tárterületén böngészve találtam nemrégiben egy frappáns definíciót a végtelenre, ami egyben a párhuzamos egyenesek tulajdonságait is új megvilágításba helyezi. Ezt és a belőle következő érdekesebb levezetéseket szeretném tömören bemutatni az alábbiakban.
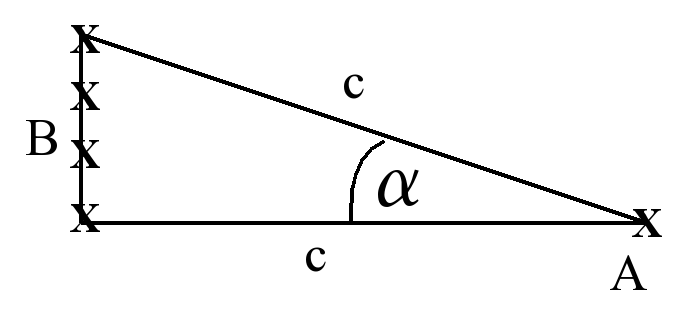
   Definíció: Végtelen az a 'c' távolság, ahonnan nézve bármely véges elemű és véges méretű 'B' rendszer bármely pontjából az 'A' szemlélőpontba húzott egyenesek párhuzamosak egymással.
   Indoklás: Amennyiben 'B' rendszer bármely pontjából az 'A'-ba húzott egyenesek nem párhuzamosak, szöget zárnak be egymással. A szög alapján pedig kiszámolható az 'AB' távolság (szögfüggvények). Ha párhuzamosak, a távolságuk meghatározhatatlan (végtelen).
   Másként megfogalmazva a dolgot: Végtelenül messze van az az 'A' pont, ahonnan nézve bármely véges 'B' dolog egy pontnak látszik. A pont természetesen az, aminek nincs része, lásd még a korábbi publikációkat az Eseményhorizonton a Ponttal kapcsolatban.
   Két nullánál nagyobb távolságra lévő ponton átmenő párhuzamos egyenesek soha nem metszik egymást. Elvileg tehát a végtelenben sem volna szabad találkozniuk. Ha viszont két pont egymástól nulla távolságra van, akkor azokat egy pontnak érzékeljük, ahogy a rajtuk átmenő párhuzamos egyeneseket is egy egyenesnek.

   A fenti ellentmondásból következik, hogy meg kell vizsgálnunk a párhuzamosság fogalmát.
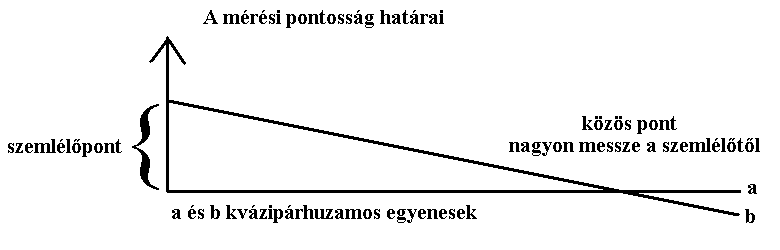
   Két egyenes akkor párhuzamos egymással, ha nincs közös pontja. Amennyiben azonban az egyenesek által bezárt szög olyan kicsi, hogy a közös pont végtelenül messze van a szemlélőtől, a közös pont észlelhetetlen, amiként a bezárt szög is mérhetetlen. Ekkor a két egyenest kvázi párhuzamosnak kell tekintenünk, nem pedig abszolút értelemben párhuzamosnak.

   Számítástechnikai nyelven megfogalmazva olyan a dolog, mintha a mérésnél "alulcsordulás" történne. A kvázi párhuzamos egyenesek nem abszolút párhuzamosak. Mivel a mérési pontosság határa (a legkisebb mérhető szög) egy tartományt fed le a számegyenesen, amelyen belül (a tartomány közepén) a nulla érték csak egy pontnyi (végtelenül kicsiny) helyet foglal el, elmondhatjuk, hogy abszolút párhuzamos egyenes csak egyféle van, míg kvázi párhuzamosokból végtelenül sokféle létezhet.
   Mindez pusztán elméleti probléma, amivel a gyakorlatban nem kell rövid távon számolnunk. Hosszabb távon azonban megváltozik a helyzet. A mérési folyamat (észlelés) időbelisége és az információ (észlelet) terjedésének véges sebessége miatt előfordulhat, hogy egy későbbi (megismételt) mérés során már mérni tudjuk a két kvázi párhuzamos egyenes közti szöget.
   Konkrétan: Ha két párhuzamosnak tűnő egyenesből megmérünk két 1000 kilométeres szakaszt, és nulla a bezárt szögük, akkor kvázi párhuzamosak. Csupán feltételezhetjük, hogy a végtelenségig párhuzamosak maradnak. Ha viszont megmérünk két 10 milliárd fényévnyi szakaszt, és nem nulla a bezárt szögük, akkor már nem párhuzamosak. Ehhez azonban meg kell várnunk, hogy a műszerünkhöz érjen az információ a két egyenes 10 milliárd fényévre lévő részéről.
   Következmény: Előfordulhat, hogy idővel minden kvázi párhuzamos egyenesről kiderül, hogy nem abszolút párhuzamos. Mivel csak végtelen ideig tartó mérés után mondhatnánk el két egyenesről, hogy kétséget kizáróan abszolúte párhuzamosak, ezért a gyakorlatban (a valóságban) csak kvázi párhuzamos egyenesek léteznek. Abszolút párhuzamos egyenes tehát nincs. Csupán elméleti konstrukcióként képzelhető el.
   A fenti következtetés természetesen igaz lesz a párhuzamos síkokra, terekre, n dimenziós kiterjedésekre is, amiből pedig az következik, hogy csak azért, mert (éppen) nem észleljük a párhuzamos világegyetemeket, még nem jelenti azt, hogy nem léteznek. Valahol, valamikor biztosan átfedésben vannak a mi világegyetemünkkel, tehát az információ is átszivárog a két világ között, valamekkora késedelemmel. Ezeket a helyeket nevezzük aztán térháborgásnak, téranomáliának, parajelenségnek, amennyiben mégis találkozunk velük.
   Egymástól aboszlúte elzárt, teljesen elszeparált létezések, teremtések tehát nincsenek. Minden ami létezik, az egy rendszert alkot. Ezzel eljutottunk a teremtésfilozófiához, amihez szépen illeszkednek az eddigiek.
   A végtelen eme definíciója azonos eredményre vezet, mint a legelső megnyilvánulás folyamatát modellező korábbi, filozófiai és matematikai konstrukciók. Amikor két Mandu (megnyilvánulatlan) létezni kezd egymás számára, Bindut (megnyilvánulót), valamint egy primer időszálat képeznek. Ezek szerint a primer időszál már az első pillanattól (t0) fogva végtelen hosszú kell legyen. Pontosabban meghatározhatatlan a hossza (a két szemlélőpont számára), mivel a hossz fogalma az őskáoszban nem definiálható, további viszonyítási pontok és főként a téridő hiányában. Az első időszál tehát a semmiben nyúlik a végtelenségtől a végtelenségig.
   Ebből következik, hogy kezdetben vala csupán a nulla és a végtelen, amik a semmi és a meghatározhatatlan matematikai reprezentánsai. Csak a későbbi forrás interakciók révén (mikor a többi Mandu is csatlakozik a létezéshez) alakulnak ki a meghatározhatatlan végtelenek relatív különbözőségei miatt a meghatározható, véges időbeli távolságok. Ekkor jelenik meg és válik értelmezhetővé az őskáoszban a kezdeti ősidő, az időszálak eseményhorizontonkénti kvantálása (időegyenes), ami a véges távolság, és az idő (a változás) alapjául szolgál majd a későbbiekben. A véges távolsággal együtt pedig megjelenik a relatív haladási sebesség (RV), a sokféle (n) haladási irány, a kétféle forgásirány (balos és jobbos), valamint a relatív forgási sebesség (RR).
   A véges számok, mennyiségek világa tehát a teremtésben (a valóságban) akkor realizálódik az Isten (szemlélő) számára, amikor az interakciók révén a végtelen feloszthatóvá válik valahány (tetszőleges) részre. Mintha azt mondanánk, hogy pl.: végtelen/10=1. Ebből pedig az következik, hogy az eseményhorizontok etalon terjedési sebessége (E=1) és az ebből levezetett térbeli távolság igazából önkényes alapmérték. Mivel mindent a kezdethez viszonyítunk, a kezdetet nincs mihez viszonyítani.
   A létezés "mérete" és "kiterjedése" így valójában lefelé és felfelé is végtelen az általunk definiált méretskálákon. Értelmetlen tehát a legnagyobb és legkisebb dolgok kutatása, keresése. Itt konkrétan a szubatomi világra és az univerzum határán túli dolgokra gondolok.
   További következmény, hogy az önmagunk számára praktikusan definiált véges értékek (mértékrendszerek) mindig csupán a műszereink hatósugaráig használhatók, azon túl értelmüket vesztik. Az észlelésünk végessége mindig meg fog akadályozni minket abban, hogy a végtelent észleljük. Másként megfogalmazva: a végtelen az, ami nem észlelhető.
   A megvilágosodás, más néven egyhegyűség állapota ezek szerint végtelenül messze van tőlünk, mert ebben a pontban a szemlélő a mindentudás állapotában van. A teljesség (minden létező dolog) egyetlen pontban van itt, tértelenül és időtlenül. Ez az a Pont (az okforrás nézőpontja), ahol a szemlélő számára minden egy. Ahonnét a Teremtő Isten szemléli az univerzumokat, időbeli észlelés nélkül, valahol a minden létező határán.
   Az őskáosz pereme a népmeséinkben az a vidék, ami az üveghegyen is túl van. Az üveghegy (átlátszó kúp, mert az idő nem valami anyagi dolog) az Öregidő Isten tachionja, ami már kint van az összes vizekből. Kisodródott a nemtér-nemidő szélére. Amerre halad, abszolúte nincs semmi.

Készült: 2004.12.14.

Következő írás

Vissza a tartalomhoz