"A
teremtés működése nem csupán logikus, de szabályos is."
A szerinó és a fotinó időhurkainak geometriai szemléltetésére lassan húsz éve használjuk már az oktaédert és a kockát, amik három dimenziós szabályos testek. Ezeknek azonban léteznek sík és szál vetületei is, mivel az időhurkot alkotó jelenpontok minden gond nélkül elhelyezhetők az alsóbb dimenziókban. Ebben az írásunkban végre bemutatjuk a két energiakvantum geometriai szerkezetét egy, két és három dimenzióban, valamint ismertetjük a szintek közti átalakítási szabályokat. A cikk logikailag a következő korábbi írásokhoz kapcsolódik, amiket érdemes elolvasni hozzá.: A három pont tétel, A tér fizikai szerkezete, A tér matematikai szerkezete, Merőlegesség n dimenzióban, Forgás n dimenzióban és A menóra titka.
1. A SZERINÓ GEOMETRIÁJA
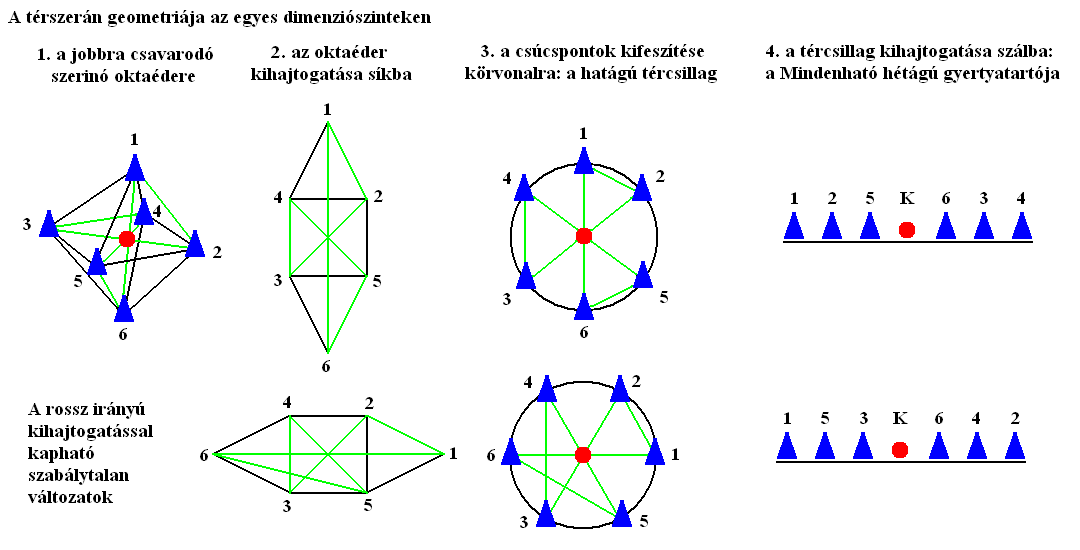
A jobbos csavarodású téridőt a jobbra csavarodó térforrás (szerinó) kelti, aminek tükörképi párja balra csavarodó és az antitéridőt kelti. A kettő megkülönböztetésének szabálya a forgás törvényeinek ismeretében könnyen meghatározható. A csúcsára állított oktaéderbe rajzolt tachion felvillanási sorrend (zárt, egyirányú hurok) akkor csavarodik jobbra, ha felülről nézve, és a felső csúcstól elindulva (tetszőleges él mentén a 2. tachionig) a 3. tachiontól órairányban keringve következik a 4. tachion. Az irányt tehát a körbejárási útvonalnak azon élre eső része szabja meg, amelyik az oktaéder függőleges forgástengelyére merőleges keringési irányban húzódik.

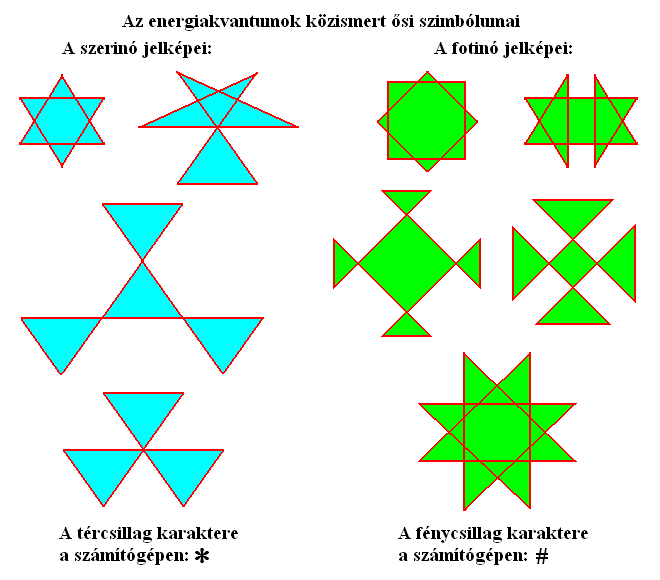
Egy 3D-s oktaéder két módon redukálható 2D-s alakzattá. Ha síkra vetítjük a csúcsait és éleit, egy hatszögbe zárt hatágú csillagot kapunk (1. ábra). Ha felvágjuk az élei mentén, hat háromszöglap elhagyásával kihajtogathatjuk síkba. Ekkor szintén egy hatszöget kapunk, ami egy négyzetből és a két szemközti oldalához illesztett háromszögből fog állni. Ha ennek csúcsait sugárirányban kihúzzuk egy köré írható kör vonalára, oly módon, hogy a csúcsok egyforma távolságra legyenek egymástól, akkor egy hatágú tércsillagot kapunk. A körbejárási útvonal ebben kétféle alakzatot vehet föl. A szabályos változatban három egy csúcsban érintkező háromszöget fog alkotni, a szabálytalan pedig egy olyan pentagramma lesz, aminek egyik hegyét levágták és a csúcsával tették vissza a helyére.
A tércsillag szintén két módon redukálható tovább 1D-s alakzattá, pontosabban szakasszá. Ha szálra vetítjük a csúcsait, a tércsillag helyzetétől függően különféle sorrendben fognak elhelyezkedni a pontok, ami nem ad egyértelmű megoldást, tehát elvetendő. Marad a hajtogatás a körvonal felvágásával, alapértelmezésben a körbejárási útvonal kezdő pontjánál, az 1. tachionnál. Mivel a szerinó jobbra csavarodik, ezért a szakasz pontjainak sorrendjét is balról jobbra haladva kell megállapítani (2. ábra). Ezzel megkaptunk egy ősi vallási jelképet, a menórát, annak hatágú, hét gyertyával rendelkező változatában.
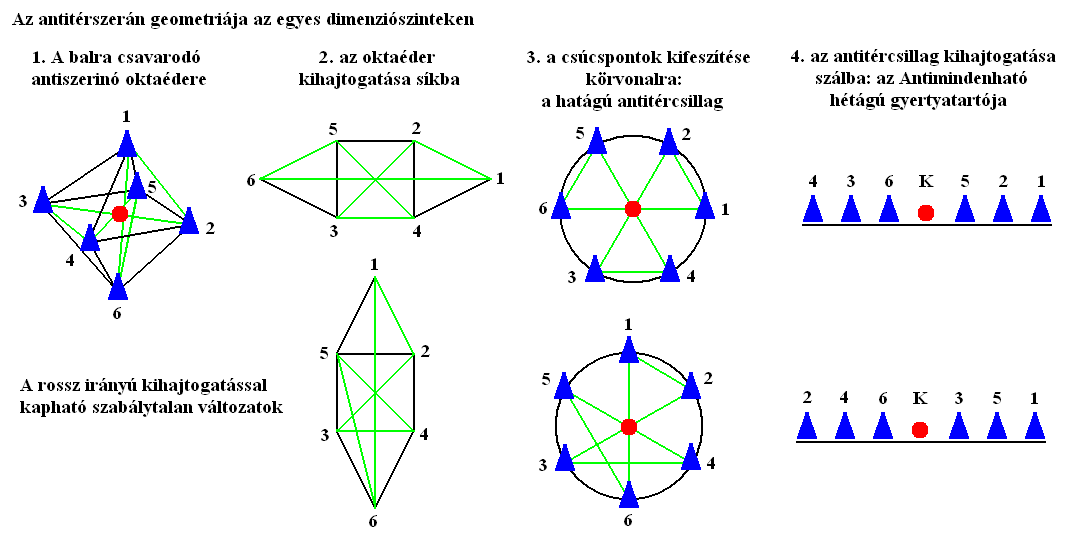
Az antiszerinót értelemszerűen balos csavarodással (3D), keringéssel (2D), illetve körbejárással (1D) kell modellezni (3. ábra). A tükrözési szabályokból következik, hogy a szerinó és antipárja 4D-ben átvihető egymásba 180 fokos elforgatással. A szerinó monász változatának nem létezik 4D-s formája, de a diász és triász szerinók egymásba ágyazódó oktaéderei már 4D-s alakzatot vesznek fel. Ennek okaival A tér fizikai szerkezete című írásunkban foglalkozunk részletesen.
2. A FOTINÓ GEOMETRIÁJA
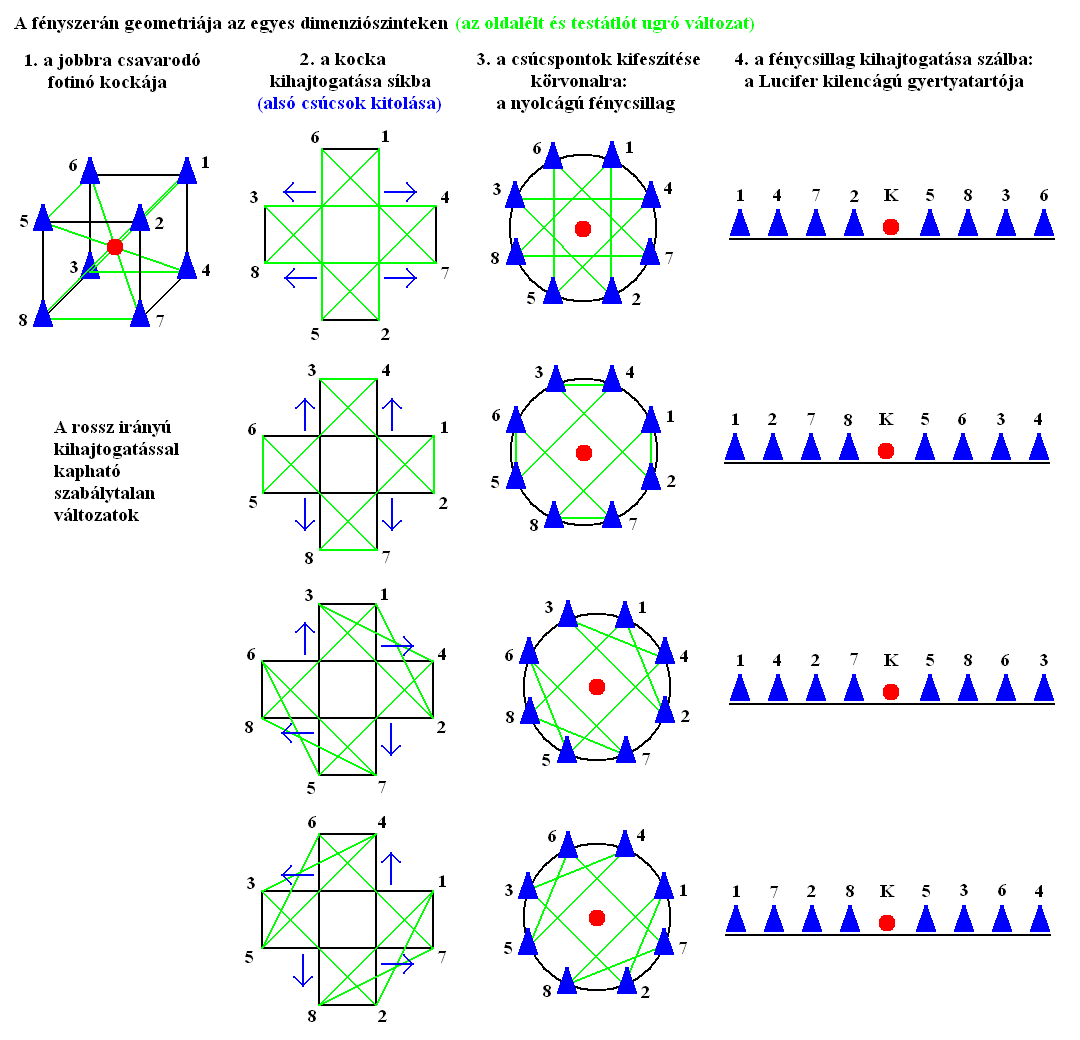
A jobbos csavarodású fényidőt a jobbra csavarodó fényforrás (fotinó) kelti, aminek tükörképi párja balra csavarodó és az antifényidőt kelti. A kettő megkülönböztetésének szabálya a forgás törvényeinek ismeretében könnyen meghatározható. A lapjára állított kockába rajzolt tachion felvillanási sorrend (zárt, egyirányú hurok) akkor csavarodik jobbra, ha felülről nézve, valamelyik felső csúcstól elindulva mindig órairányban keringve következnek a tachionok. Az irányt tehát a körbejárási útvonal felületre (élre vagy lapátlóra) eső részeinek keringési irányai szabják meg.
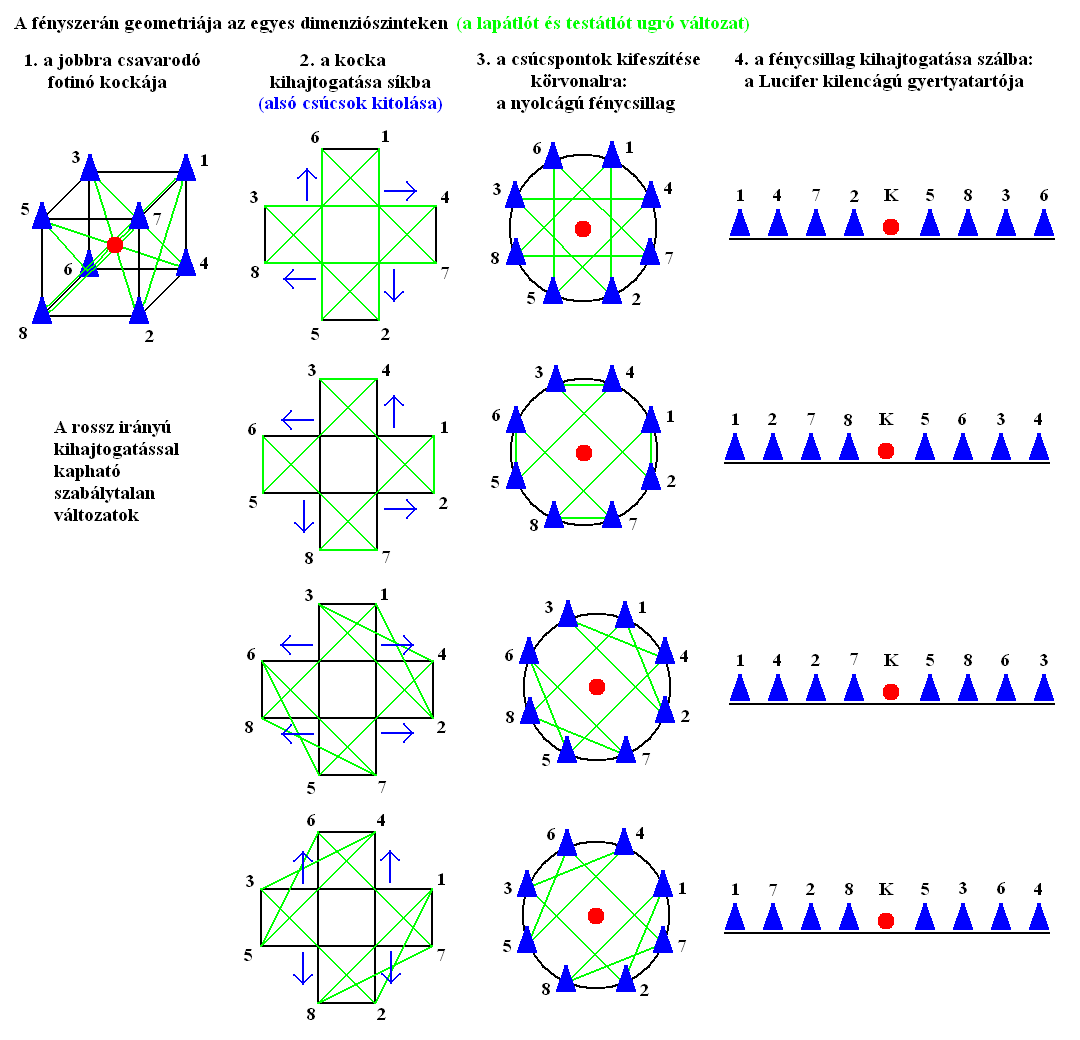
A 3D-s fény esetében a tachionok felvillanási sorrendje kétféle, fizikailag egyenértékű útvonalat követhet. Az egyiknél az oldalélek és testátlók mentén halad, a másiknál a lapátlók és testátlók mentén a körbejárási útvonal. Ezek 2D-s és 1D-s változatai azonosak lesznek, csak a leképzés módja lesz eltérő, amivel megkapjuk őket. Hogy miért van a fotinónak kétféle térbeli körbejárási útvonala, azt egyelőre nem tudjuk, de lehetséges, hogy az időhurok tachionjainak behúzási tartományával lesz kapcsolatos a dolog.

Egy 3D-s kocka két módon redukálható 2D-s alakzattá. Ha síkra vetítjük a csúcsait és éleit, egy hatszöget kapunk az átlóival (4. ábra). Ha felvágjuk az élei mentén, a felső lapjának elhagyásával kihajtogathatjuk síkba. Ekkor egy egyenlő szárú keresztet kapunk, ami öt négyzetből fog állni. Ha ennek csúcsait sugárirányban kihúzzuk egy köré írható kör vonalára, oly módon, hogy a csúcsok egyforma távolságra legyenek egymástól, akkor egy nyolcágú fénycsillagot kapunk. A körbejárási útvonal ebben háromféle alakzatot vehet föl. A szabályos változatban elsődlegesen egy nyolcágú csillagot fog alkotni, másodlagosan pedig egy négyzetet, a csúcsaival érintkező négy kis háromszöggel. A szabálytalan változat pedig egy furcsán széthúzott hatágú csillag lesz, amit két vonal köt össze (5. ábra).
A fénycsillag szintén két módon redukálható tovább 1D-s alakzattá, pontosabban szakasszá. Ha szálra vetítjük a csúcsait, a fénycsillag helyzetétől függően különféle sorrendben fognak elhelyezkedni a pontok, ami nem ad egyértelmű megoldást, tehát elvetendő. Marad a hajtogatás a körvonal felvágásával, alapértelmezésben a körbejárási útvonal kezdő pontjánál, az 1. tachionnál. Mivel a fotinó jobbra csavarodik, ezért a szakasz pontjainak sorrendjét is balról jobbra haladva kell megállapítani (6. ábra). Ezzel megkaptuk a menóra nyolcágú, kilenc gyertyával rendelkező változatát.
Az antifotinót értelemszerűen balos csavarodással (3D), keringéssel (2D), illetve körbejárással (1D) kell modellezni. A tükrözési szabályokból következik, hogy a fotinó és antipárja 4D-ben átvihető egymásba 180 fokos elforgatással. A fotinó monász változatának azonban létezik egy 4D-s formája is, ami érdekes módon nem hiperkocka, hanem hiperoktaéder alakú. Ennek okaival A tér fizikai szerkezete című írásunkban foglalkozunk részletesen.
3. KÖZISMERT ALAKZATOK
Mivel az energiakvantumok geometriai szerkezetének tudása ősidők óta megvan az emberiség számos népcsoportjának művészi és vallási motívumai között, ezért valószínűleg senkinek nem okoznak meglepetést az alábbi képek (7. - 8. ábrák). Így máris érthető, miért olyan kedvelt és rendszeresen alkalmazott formákról van szó.
Vissza a tartalomhoz