A körkerületi paradoxon egy régóta ismert geometriai probléma, amit érdekességképpen közlök az időmatematikai anyagok kiegészítéseként. Ez a látszólag egyszerű feladat jól példázza, milyen alapvető bajok vannak a hagyományos matematikai apparátusunkkal, amire régóta ráférne a teljes felújítás.
Rajzoljunk két kört, közös origóval, tetszőlegesen eltérő sugárral egymás köré. Ezután húzzunk egyeneseket az origóból a kisebbik kör vonalának minden pontjába, majd hosszabbítsuk meg ezeket tovább, hogy átmenjenek a nagy kör vonalán is. Azt fogjuk látni, hogy ahány pontja van a kis körnek, annyi egyenest húzhatunk kifelé. Ezek tehát annyi ponton fogják metszeni a nagy kört, ahány pontja van a kis körnek. Viszont szükségszerű, hogy a nagy kör vonalán számos pont kimarad, mert két szomszédos egyenes közé esik.
Most fordítsuk meg a műveletet és húzzunk egyeneseket a nagy kör minden pontjából az origóba. Ekkor is azt látjuk, hogy a kis körnek minden pontján keresztül halad egy egyenes. Vagy mégsem?
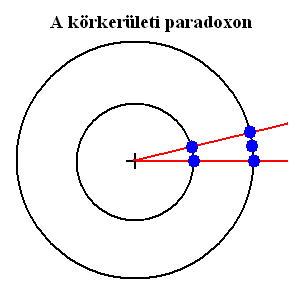
Azt elmondhatjuk, hogy az első esetben, a kis kör pontjain át húzva kifelé az egyeneseket a nagy kör vonala több pontból áll, mint a kicsié. Ez normális (természetes), mert a kerülete is nagyobb. De a nagy kör pontjaiból húzva befelé az egyeneseket azt látjuk, hogy elvileg a kis kör minden pontján átmegy valamelyik. A kis kör tehát ugyanannyi pontból áll, mint a nagy kör, ami nem tűnik normálisnak. Ha ez nem így van, akkor egyes egyenesek a kis kör szomszédos pontjai között mennek át, mely esetben a körvonal nem lehet folytonos, ami ellentmondás.
Azt gondolnánk, hogy ez a paradoxon csak akkor áll fönn, ha véges számú egyenest húzunk a körvonalaktól az origóba. Végtelen számú egyenesnél ugyanis mindkét körvonal végtelen mennyiségű pontból áll, vagyis nincs köztük különbség. Ez esetben viszont, a körvonal pontjai közt egyenlő távolságot feltételezve (ami végtelenül kicsiny távolság ugyan, de akkoris fix és nullánál nagyobb távolságnak kell tekintenünk bármely két szomszédos pont között), minden véges sugarú kör kerülete ugyanannyi pontból áll: végtelen számú pontból. Tehát két eltérő hosszúságú körvonal egyforma mennyiségű pontból áll, ami megint csak paradoxon.
Egy véges hosszúságú körvonal csak akkor állhat végtelen számú pontból, ha a pontok végtelenül közel vannak egymáshoz, gyakorlatilag nulla távolságra. Ha viszont nulla a szomszédos pontok közti távolság, akkor a kör kerülete is nulla (0 pont + 0 távolság + 0 pont = 0 hossz), mert a távolság értelmezhetetlenné válik. A nulla kerületű kör sugara is nulla, tehát a kör azonos lesz egy ponttal. Egy pont viszont semmiképpen sem tekinthető körnek (sőt még protokörnek sem), mert nincs sugara.
Azt tudjuk, hogy két végtelen mennyiség között nincs különbség, mert végtelen csak egyféle van (fogalmának abszolút értelmében). Vagyis a végtelenül kicsiny sugarú és kerületű kör is csak akkora, mint a végtelenül nagy. Ha megengedjük, hogy többféle (n féle) végtelen hosszúság legyen a geometriában, akkor ezzel csak látszólag oldjuk fel a problémát, mert a kétféle végtelen közti különbségnek ugyancsak végtelennek kell lennie, különben visszajutunk a kezdeti végességi problémához. A végtelen különbség nagyságának többféle meghatározásával viszont újabb ellentmondást hozunk létre, tehát csak eltoltuk a problémát, de nem oldottuk meg.
Közelítsük meg a feladatot egy másik irányból. A végtelen sugarú kör vonalának minden pontjából az origóba húzott egyenesek által bezárt szögek végtelenül kicsinyek. Gyakorlatilag nulla fokosak. Ekkor viszont a szomszédos egyenesek párhuzamosak. Ez megint paradoxon, mert ha párhuzamosak, akkor nem haladhatnak át soha ugyanazon a ponton (origón), vagy ha mégis, akkor nem párhuzamosak (csak kvázi párhuzamosak) vagy nem egyenesek (kvázi egyenesek), hanem görbék. Ez újabb paradoxonok sorozatához vezet.
Ha a végtelen sugarú körvonal két tetszőleges pontján átmenő egyenesek abszolút egyenesek, és véges (nem nulla) szöget bezárva egymással metszik az origót, úgy a kör két pontja végtelenül messze van egymástól. Tehát köztük a körvonalon végtelen sok további pont van. Így a két egyenes által bezárt szög bármely (nullánál nagyobb) értékéhez ugyanolyan végtelen hosszú körív tartozik. Ami szintén paradoxon, hogy bármely két szöghöz egyforma hosszú körív tartozzon.
Bármerről közelítsük is meg a problémát, minden esetben bele fogunk futni a végtelennel kapcsolatos műveletekbe és ellentmondásokba. Ennek a paradoxonnak tehát sem a véges, sem a végtelen számok tartományában nincs megoldása. Mindez csupán annyit bizonyít, hogy nulla méretű pontokból nem lehet véges méretű kiterjedéseket, kört vagy egyenest összeállítani holmi egymás mellé rakosgatással, ahogy azt a klasszikus matematika teszi.
Ha mindezt az időmatematika időpontjaival csináljuk meg, ott a paradoxon értelmét veszti, mert a szomszédos pontok közt definiált időbeli távolság mindig véges érték. Az időegyenes tehát úgy folytonos, hogy közben kvantált, s a két leképzés nem áll egymással ellentmondásban. Így a nagy körvonaltól befelé húzva az egyeneseket azt fogjuk kapni, hogy több szomszédos egyenes a kis kör vonalát ugyanazon pontban metszi, tehát gyakorlatilag eggyé válik. Mivel a dimenzió tétel lehetővé teszi, hogy az 1D-s egyenes egy pont vagy két pont vastag legyen, ellentmondásmentesen kezelhetők az egymáshoz nagyon közel húzott egyenesek és ezek összeolvadása.
Készült: 2007.07.05.
Következő írás
Vissza a tartalomhoz