A TÉRKONVERTER MŰKÖDÉSE


Ezen írás megértéséhez feltétlenül ismernie kell az Olvasónak a forgással kapcsolatos korábbi publikációkat, mivel takarékosságból számos dolgot nem magyarázunk el újra. A térkonverter egy olyan műszaki berendezés, ami komplex forgatások segítségével képes térprodukciót vagy térredukciót előidézni, a saját hullámterének manipulációjával. Ennek elméleti alapjairól szólnak az alábbiak. Gyakorlati jelentősége a térváltás technológia kifejlesztése mellett az n dimenziós tértechnológiák alkalmazása kapcsán van a térkonverternek, amivel később még számos írásunkban szeretnénk foglalkozni részletesen.

1. FORGATÁSOK

Ha egy pontot keringetni kezdünk egy 1D-s forgástengely körül, akkor a mozgástere lokálisan 1D-s lesz, globálisan 2D-s, míg a forgástengely kilóg a síkból a 3D-be. Ennek a pontnak a kiáradó hullámtere a síkban egy tömör, felfúvódó spirálkör lesz. Ha a keringés origójába állítunk egy második forgástengelyt is, ami úgy merőleges az elsőre, hogy benne van a keringés síkjában, és ekörül is elforgatjuk (különféle sebességekkel) a körvonalat, amin a pont halad, akkor a két keringés eredőjeként egy gömbfelszín mentén fog mozogni a pont. Ahol egy önmagába záródó spirálvonalat ír le a pont, aminek két pólusa van a gömbfelszínen ott, ahol metszi azt a második forgástengely. A pólusokban a spirálvonal többször metszi önmagát, a második forgástengely körüli keringés sebességétől függően. A pont mozgástere ekkor lokálisan 2D-s, globálisan pedig 3D-s lesz, míg a kiáradó hullámtere egy tömör, felfúvódó spirálgömböt alkot.
Azt gondolnánk, ha egy harmadik forgástengelyt is belerakunk ebbe a rendszerbe, ami szintén merőleges az első és a második tengelyre is, akkor ekörül elforgatva a spirálgömböt, a pont egy gömbtérfogatban fog mozogni. Aminek mozgástere lokálisan 3D-s, globálisan 4D-s lesz, a hullámtere pedig egy kiáradó spirálhipergömb lesz. De ez nem így van, mivel a páratlan térdimenziószámú közegekben a beágyazott forgástengelyek körüli forgatások nem növelik meg a térdimenziószámot. Csak az onnan kilógó forgástengelyek, amik egy pontban metszik az origót, lehetnek képesek erre. Egy pont körül viszont nem lehet egy 3D-s testet körbeforgatni a 3D-ben. Felmerül akkor a kérdés, hogyan lehet, illetve egyáltalán lehet-e olyan komplex forgatást létrehozni, ami egy adott nD-s térdimenzión belül mégis olyan kiáradó hullámteret eredményez, ami n+1D-s?
Azt tudjuk, hogy a pont forgása nem emeli a beágyazási környezetének térdimenziószámát, a keringése viszont igen. A keringést azonban többféleképp is meg lehet valósítani a tengelyek különféle elhelyezésével egymáshoz képest. Két forgástengelyt nem csak úgy lehet elhelyezni a 3D-ben, hogy a keringés origójában merőlegesen metsszék egymást, hanem sok más módon is. Ha például a második tengely érintője a körvonalnak a síkban, egy olyan lokálisan 2D-s mozgásteret kapunk (tóruszfelszínt), ami globálisan 3D-s, míg a kiáradó hullámtere (spiráltórusz) szintén egy 3D-s spirálgömb lesz. Ha nem érintője a tengely a körvonalnak, a tórusz geometriailag lehet gyűrű (pontosabban úszógumi) vagy belül dupla sűrűségű fánk is.
Ha a második forgástengely úgy érintője a körvonalnak, hogy közben párhuzamos az első forgástengellyel a 3D-ben, akkor a pont egy tömör körlap felszínén fog mozogni, aminek a sugara egyenlő az elsődleges körvonal átmérőjével.



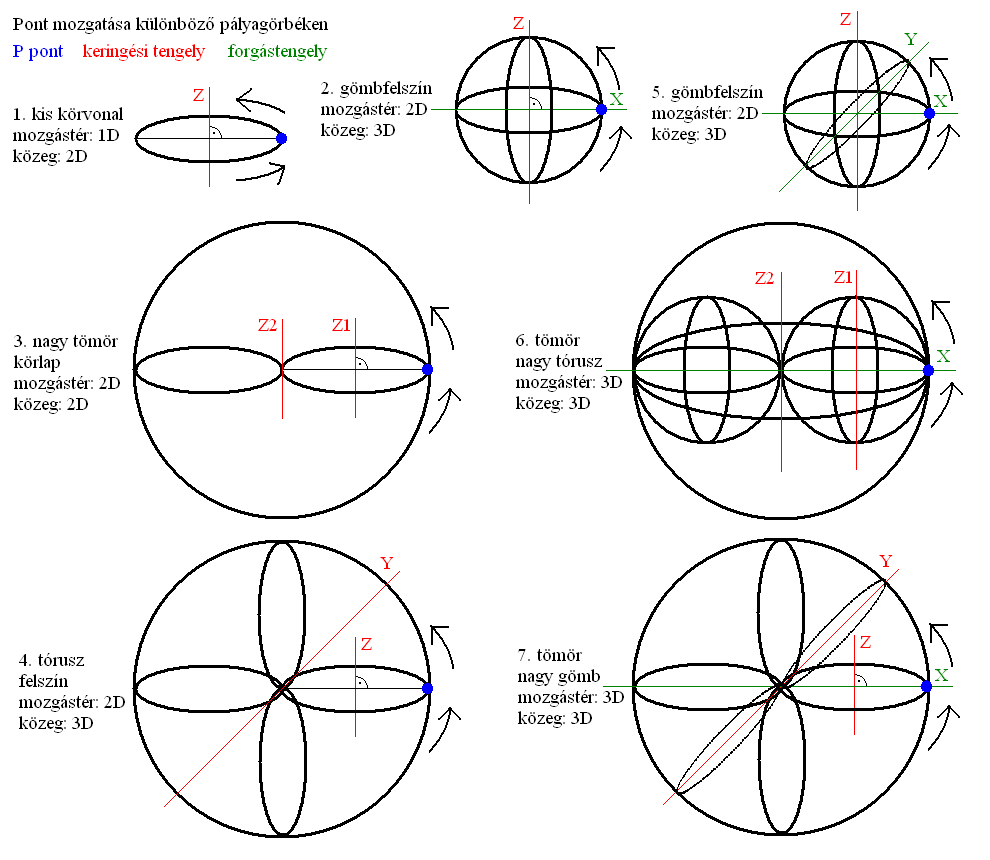
Ha a pont által bejárt gömbfelszínt egy harmadik forgástengely körül is elforgatjuk, annak elhelyezkedésétől függően gömbfelszínt, tömör gömböt vagy különféle tóruszokat kapunk. Ez esetben csak a pont mozgási sebessége nő meg a mozgási útvonalának elnyújtásával, de ettől még a hullámtere ugyanúgy 3D-s marad.
Amint az látható, a probléma megoldásához nem elegendő a geometriai megközelítés. Topológiai modellezésre is szükség van a kívánt eredmény megtalálásához. Ezért folytassuk vizsgálódásunkat azzal, hogy az egyes komplex mozgások során a pont által bejárt kiterjedések topológiai elemzését végezzük el.

2. HAJLÍTGATÁSOK ÉS KILAPÍTÁSOK

A körlap egy olyan 2D-s síkbeli kiterjedés, ami a 3D-s teret két részre osztja: fentre és lentre. A gömbfelszín is 2D-s, de ez a 3D-t másként osztja két részre: bentre és kintre. A körlapból úgy csinálhatunk gömbfelszínt nyújtással és hajlítással, ha a 3D-ben meghajlítjuk, félgömböt készítve belőle, majd a körvonalat összehúzzuk egyetlen pontba. Mintha bezárnánk egy zsák száját.
A gömbtérfogat (tömör golyó) egy olyan 3D-s térbeli kiterjedés, ami a 4D-s túlteret két részre osztja: anára és katára. A hipergömbtérfogat is 3D-s, de ez a 4D-t másként osztja két részre: bentre és kintre. A gömbtérfogatból úgy csinálhatunk hipergömbtérfogatot nyújtással és hajlítással, ha a 4D-ben meghajlítjuk, félhipergömböt készítve belőle, majd a gömbfelszínt összehúzzuk egyetlen pontba. Azért pontba és nem szálba, mert gömbszimmetrikus objektumról van szó, ahol a szálba húzás már irányultságot jelentene, ami itt nem megengedhető. Csak ha szögletes objektumokkal dolgozunk, akkor lehet szálba összehúzni a kiterjedés felszínét (például egy négyzetet hengerbe vagy egy kockát hiperhengerbe).
Ha a gömbfelszínt gyurmázással kilapítjuk a 2D-s síkba, akkor egy dupla rétegű körlapot kapunk, amiben a keringő, mozgó pont önmagával való ütközés nélkül tud oda-vissza mozogni a síkban, mivel a körlap fizikailag két pont vastagságú marad. Ennek megfelelően ha a hipergömbtérfogatot gyurmázással kilapítjuk a 3D-s térbe, akkor egy dupla rétegű gömbtérfogatot (tömör golyót) kapunk, amiben a keringő, mozgó pont önmagával való ütközés nélkül tud oda-vissza mozogni a térben, mivel a golyó fizikailag két pont vastagságú marad. Ez a matematikai tulajdonság szorosan kapcsolódik az időfizikából ismert tachion kettős idősűrűségű hullámterének szerkezetéhez, de most ne térjünk el a tárgytól (akit érdekel, gondolja végig a következményeket).
A fő kérdés most az: tudunk-e a 3D-n belüli elforgatásokkal és keringésekkel olyan dupla sűrűségű hipergömbtérfogatot csinálni, ami ugyanakkor csak 3D-s? Pontosabban 3D-be kilapított? A válasz egyértelműen igen. Egy olyan kettős áramlási irányú, tömör 3D-s gömböt kell hozzá konstruálnunk, ami ráadásul félspínű is, mert különben az ellenirányban forgó és keringő pontok mozgásvektorai folyamatosan kioltanák egymást.
Ha egy tóruszfelszínt kiforgatunk tömör gömbbé, akkor a tóruszt alkotó pontok fél fordulatonként kitöltik a gömb térfogatát, tehát fordulatonként kétszer bejárják a pontok a gömbtérfogat minden pontját. Csak éppen azonos irányban, mert ez esetben nem keletkezik ellenirányú forgás. Ez még csupán egy 3D-s tömör gömböt fog eredményezni, ami ugyan dupla belső pontsűrűségű, de önmagában még nem lesz 4D-s kiterjedésű.
Ha viszont ezt a tömör gömböt egy újabb forgástengely körül is elforgatjuk, akkor fél fordulatonként az egész gömb körbefordul félig (180 fokban), ami azzal jár, hogy a második félfordulat során a tóruszfelszínen mozgó pontok már ellenirányban forgó, áramló módon szaladnak végig. Mintha a jobbos csavarodású tóruszból hirtelen balos lenne, ráadásul tértükrözés nélkül, mivel időben egymás utáni (és nem egyidejű) állapotokról van szó. Így nem fogja magát a rendszer folyamatosan kioltani. Ez pedig már megfelel a 3D-be kilapított, dupla sűrűségű és ellenirányú áramlással rendelkező hipergömbtérfogat definíciójának.
Ráadásul ez a komplex mozgás (örvénylés) úgy jön létre, hogy a kezdeti 0D-s pontot összesen négy forgástengely körül mozgatjuk meg. Ebből az első kettő keringés lesz (a pontot ehhez eltoljuk a tengelytől, ami megfelel a normálvektor mentén történő futásnak, helyváltoztatásnak) a második kettő pedig forgás. Aki még emlékszik rá: mindez megfelel az időmatematikában a 4D-s tengelypáros tér keltési szabályának. Lásd: A tér matematikai szerkezete (2007) című írást az Eseményhorizonton.


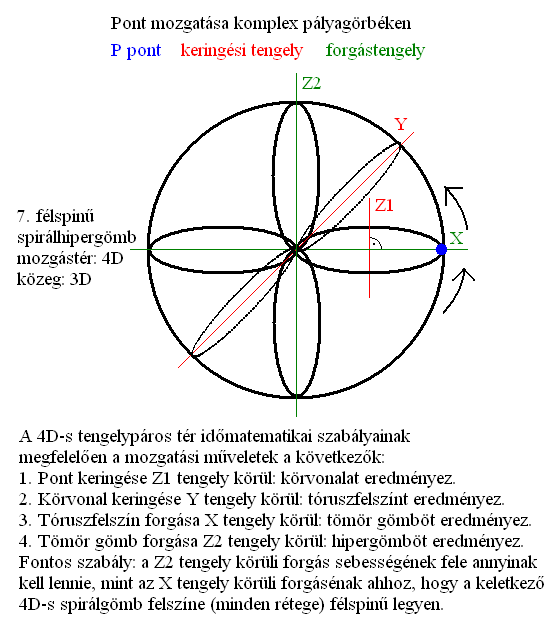
Az első és a negyedik forgástengelyek fél fordulatonként párhuzamosak lesznek egymással, ahogy a második és a negyedik is fél fordulatonként fedik egymást. A negyedik tengelynek pedig fele olyan gyorsan kell forgatnia a rendszert, mint a harmadiknak, így lesz a spirálgömbfelszín félspínű. Kétségtelen tény, hogy elsőre kissé nehéz ezt átlátni a rajzok alapján, de a komplex forgások matematikáján edződött képzelettel simán megoldható a feladat.
Kiegészítés: A forgó pont kiterjedő hullámtere időben mindig nő (nyúlik, tágul, dagad), ami a normálvektornak köszönhetően helyváltoztató mozgást jelent. Ezt spirállal ábrázoljuk, amiből következik, hogy minden olyan forgás és keringés, amihez tágulás, kiáradás társul, valójában spirálmozgás. Ebből következnek az alábbi elnevezések.: A forgó szálat nevezzük spirálszálnak. A forgó sík neve ennek megfelelően spirálkör, a forgó tér a spirálgömb, a forgó túltér a spirálhipergömb, a forgó kültér a spirálextragömb, a forgó feltér pedig a spirálultragömb.
Az eddigi modellek alapján látható, hogy a tórusz és a gömb az a két forma minden térdimenzió szinten, amik szeretik egymást váltogatni. A forgó pontnak ugyan nincs kiterjedése, de topológiailag mégis csak ekvivalens a tórusszal. Ha a pont eseményhorizontja kiárad, az a sugárirányú normálvektoroknak köszönhetően olyan időteret alkot, ami ekvivalens a gömbbel. A természetben (a létezésben) tehát csak ez a kétféle geometriai szerkezet fordul elő fizikailag, mint eredeti, transzcendens ősforma. Minden más forma ezek kölcsönhatásából keletkezik a teremtés káprázatában.

3. KÖVETKEZMÉNYEK

Mivel ilyen 4D-s spirálhipergömbi túltérből kétféle lehetséges, balos és jobbos csavarodású - a forgási és keringési irányok eredő irányai miatt -, ezért nem mindegy, melyiket valósítjuk meg ténylegesen, fizikailag a működő térkonverter készülékkel. Nagyon fontos (pontosabban életbevágó), hogy jobbos forgásokkal működjön, mert akkor lesz belőle téridő. Ha megfordítva a forgásirányokat balos hullámteret csinálunk, az antitéridőt kelt maga köré, ami a rendszer forgásakor a kritikus sebességet elérve robbanásszerűen megsemmisíti önmagát és a környezetében lévő anyagokat is. Szó szerint annihilálódik a berendezés, a balfék kísérletezővel együtt. Plusz megsemmisül a robbanás hatósugarán belül még egy csomó minden, ami a ketyere méretétől és tömegétől függően akkora is lehet, mint egy hidrogénbomba robbanás halálzónája. Vagyis nem játék a tértechnológia! Mérnök urak, tessék nagyon vigyázni!
A félspínű forgás lényege, hogy mialatt fentről lefelé haladva a pont megtesz fél kört, azalatt a függőleges tengely körül elfordul negyed kört. Így a teljes kör megtétele után abból az irányból érkezik vissza a kiindulási pontjába, amerre elindult. A második kör megtétele ugyanaz lesz, csak az ellenkező irányba. Ahhoz, hogy tömör legyen a hullámtér, bőven elég, ha a mozgatott pont fizikailag a berendezésben egy körgyűrű lesz, de tömör tárcsát használva még jobb eredményt érhetünk el. A lényeg, hogy a második forgástengely egy pontban érintse meg az első forgástengely körül leírt kör szélét (vonalát), mert akkor lesz teljesen tömör a hipergömb, belső lyuk, illetve duplázódás nélkül.
Most, hogy már értjük, hogyan lehet egy nD-s kiterjedésben komplex forgások segítségével n+1D-s kiterjedésű hullámteret generálni, az erősebb matematikusok azzal is megpróbálkozhatnak, hogy kiterjesszék a modellt n+2D-re és még följebb. Vagyis elméletileg semmi akadálya a tetszőlegesen magas térdimenziószámú spirálgömbi hullámterek létrehozásának. Csak újabb és újabb forgástengelyeket kell megfelelően hozzáadni az eddigiekhez. A gyakorlatban azonban számos műszaki problémával és fizikai akadállyal kell megküzdenie annak, aki ilyesmire adná a fejét. Egyrészt a forgó tárcsa anyagának ellent kell állnia az egyre extrémebb gyorsulásnak. Minél gyorsabban forog a rendszer, annál erősebb és tisztább (szaggatás mentesebb) a hullámtere, viszont annál nagyobb terhelés éri a szerkezetet (csapágyazás, a forgó tárgyakat összetartó erő, stb). A meghajtómotorok terhelhetőségének is vannak határai, egyszóval mérnöki szempontból csöppet sem könnyű a feladat.
A működő térkonverter közelében (valamekkora hatósugáron belül) szükségszerűen 4D-s téranomáliák jelentkeznek, amik azonnal tönkreteszik az összes elektromos rendszert (az elektronok vezetőkből való megszökése miatt), és mindenféle, szinte elképzelhetetlen őrületet eredményeznek. Ezek egy része helyrehozhatatlan károkkal jár és fantasztikus filmeket megszégyenítően bizarr és látványos változásokat okoz a környezetben. Éppen ezért ilyen kísérleteket csak a legnagyobb óvatossággal szabad végezni, lehetőleg távol minden lakott helytől, a végrendelet megírása és letétbe helyezése után.
Bár a tértechnológia veszélyei őszintén elborzasztóak, megfelelő kézben mégis roppant hasznosak lesznek ezek a fejlesztések. A térugró űrhajók számára alapvető berendezés a térváltó hajtómű, ami lényegében egy szabályozható térkonverter. A térablak technológia is elképzelhetetlen az 5D-s kültér generátorok nélkül (erről még publikáltunk semmit, bár régi kutatási anyagról van szó). A mesterséges gravitáció generátorok és a legegyszerűbb teremtőgépek sem működhetnek térkibővítők nélkül, és természetesen sok más eszközhöz is szükség lesz rájuk, amiket most még elképzelni sem tudunk.

Készült: 2007.12.15. - 2009.12.14.

Vissza a tartalomhoz