A GRAVITÁCIÓ TERJEDÉSI SEBESSÉGE

Az időfizikai világmodellben a létezés alaptörvényének tekintjük, hogy a gravitációs hullámok emanációs sebességgel terjednek kifelé a forrásukból, ami megfelel a fénysebességnek. De a gyakorlatban mi igazolja ezt mérhető módon? Honnan tudjuk, hogy a gravitáció nem végtelenül gyorsan terjed kifelé a tömegközéppontból, ahogy azt egyes fizikusok állítják, a téridőt behorpasztó görbületként próbálva ábrázolni a tömegvonzást? Az alábbiakban erre mutatok egy szemléletes bizonyítékot: az elliptikus bolygópályákat.

A következők megértéséhez érdemes megismerni Kepler törvényeit, amik leírják a bolygók keringésének szabályait a Nap körül, de nem adnak magyarázatot ennek fizikai okára. Látszólagos magyarázatul a kéttest probléma szolgál, ami Newton óta egzaktul megoldható matematikailag, épp csak ugyanúgy nem ad valódi választ a jelenség fizikai okára. Mintha évszázadokon át mindenki lazán megfeledkezett volna erről az apróságról, hogy válasz nélkül maradt a kérdés. A matematikai válasz ugyanis nem fizikai válasz egy fizikai jelenségre. Pedig fontos dologról van szó, mert lényegében ez tartja össze az egész univerzumot és meghatározza a bolygók, holdak, üstökösök, csillagok, galaxisok mozgását egymáshoz képest.

1. KEPLER TÖRVÉNYEI

1. Törvény: A bolygók pályája ellipszis, annak egyik fókuszpontjában van a Nap. Az ellipszis azon pontok halmaza a síkban, amik két adott fókuszponttól azonos távolságösszegre vannak.

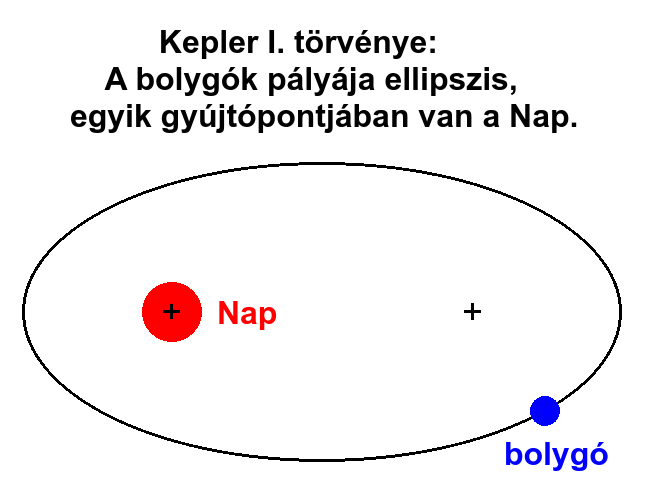
Azt viszont nem árulja el a törvény, hogy melyik fókuszpontban és miért pont abban kell lennie a Napnak? Úgyhogy ezzel a kérdéssel feltétlenül foglalkoznunk kell!

2. Törvény: A bolygók vezérsugara (ami összeköti a bolygót a Nappal) azonos idő alatt azonos területet súrol a pályasíkon.

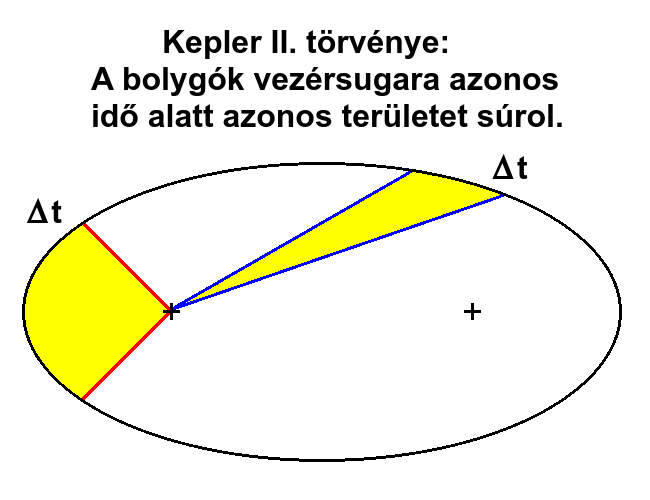
Ebből következik, hogy a bolygók gyorsabban mozognak a pályavonalukon a Naphoz közelebb, mint távolabb. Azt viszont nem árulja el a törvény, hogy miért? Pedig itt óriási erőkről van szó, ami képes a nagy tömegű égitesteket folyamatosan felgyorsítani, majd lelassítani a pályájukon, a rendszer élettartama alatt akár sok milliószor vagy milliárdszor is! Úgyhogy ezzel a kérdéssel is feltétlenül foglalkoznunk kell!

3. Törvény: A bolygók keringési idejeinek (T) négyzetei úgy aránylanak egymáshoz, mint az ellipszispályák fél nagytengelyeinek (a) köbei. Azaz: a^3/T^2=állandó.

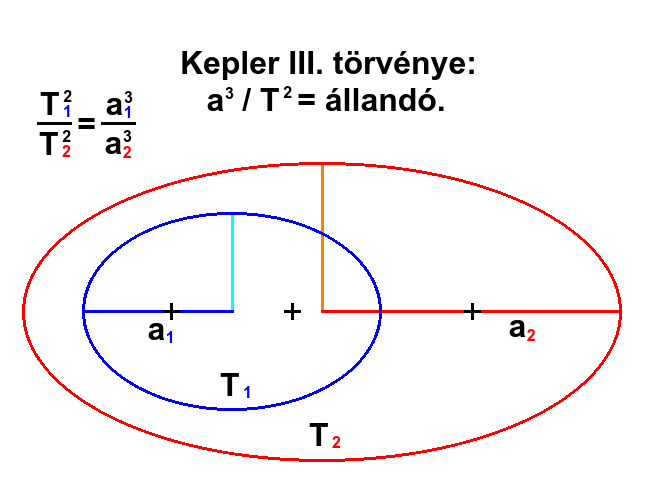
Ebből következik, hogy a Naptól távolabb keringő bolygók keringési ideje nem a megtett útjuk hosszával arányosan nagyobb, mert lassabban mozognak a pályájukon. Azt viszont nem árulja el a törvény, hogy miért mozognak lassabban a távolabbi bolygók? Úgyhogy ezzel a kérdéssel is feltétlenül foglalkoznunk kell!

2. FUTÁSIDŐ

Az anyagi részecskék fénykvantumokból állnak. Ezek sokasága alkotja az égitest, mint anyagi halmaz tömegét, aminek komplex időhullámterében az egyes hullámrétegek taszítási vektorainak eredője sugárirányban befelé mutató irányú (a forrásuk felé), amit gravitációs vonzásnak nevezünk. Ennek nagysága a 3D-s téridőben a távolsággal négyzetes arányban csökken, mivel kétszer akkora távolságban negyedakkora a közel gömb alakú égitest közel kör alakú hatáskeresztmetszete (síkra vetített felülete).

Az időhullámok emanációs sebességgel áradnak ki a forráspontjukból, azaz a fénykvantumok hullámrétegei fénysebességgel terjednek kifelé belőlük a végtelenbe, gömbszerűen. Ebből következik, hogy minél messzebb van két fénykvantum egymástól, annál tovább tart, mire az egyik hullámai elérik a másikat. Ez a távolsággal arányos futásidő, aminek döntő jelentősége van a fizikai kölcsönhatások működése szempontjából.

Mivel az univerzumban minden fénykvantum és anyagi részecske folyamatosan és megállíthatatlanul mozog a rajta áthaladó, minden irányból érkező időhullámok taszigálása miatt, a források azalatt is elmozdulnak, amíg a körülöttük lévő többi forrás hullámai elérik őket. Tehát B forrás (bolygó) az 1. pontban látja N forrást (Nap), miközben N valójában már a 2. pontban tartózkodik, jóval odébb. Ezért B-re úgy hat N, mintha még mindig az 1. pontban lenne. Vonzóerő esetén így B az 1. pont felé fog elmozdulni (körülötte akar keringeni), tehát nem a 2. pontban lévő N felé. Ugyanígy N is máshol látja B-t, mint ahol valójában van. Minél nagyobb B és N közt a térbeli távolság, illetve minél gyorsabban mozognak egymáshoz képest, annál nagyobb lesz az eltérés az 1. és 2. pont között. Tehát annál nagyobb lesz a fizikai kölcsönhatás irányának kényszerű eltérése az aktuális valóságtól. Ha a gravitáció végtelenül gyorsan terjedne, nem lenne eltérés a vonzásirány és az égitest pozíciója közt, vagyis a keringési pálya kör alakú lenne, nem ellipszis.

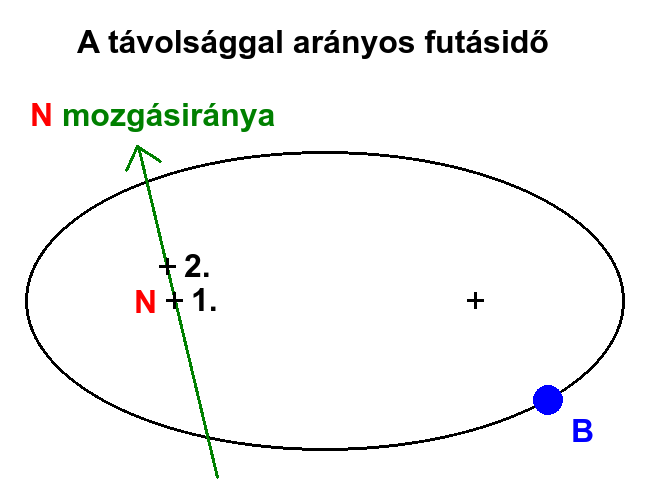
3. MAGYARÁZATOK

Kepler 1. törvényének magyarázata:

A bolygók azért keringenek ellipszis alakú pályákon, mert a fókuszpontban lévő Nap véges sebességgel mozog az űrben, egyrészt a galaxis tömegközéppontja körül keringve, másrészt az egész galaxissal együtt mozogva az űrben, a lokális galaxishalmaz részeként. Tehát folyamatosan elmászik a körpálya középpontjából, ellipszissé megnyújtva azt. Ebből következik, hogy a Nap mindig abban a fókuszpontban tartózkodik, illetve ahhoz van közelebb, amelyik közelebb van a pályavonalához. Mivel a bolygók pályái által alkotott ekliptika síkja nagyjából 60,2 fokos szöget zár be a galaxisunk egyenlítőjével, a Nap folyamatosan kimozdul ebből a síkból, majdnem a saját északi pólusa irányába haladva. Így a bolygók mindig lemaradva tőle, spirálpályákon keringenek körülötte a galaxis középpontjából nézve.

A Nap kb. 220 km/s sebességgel kering a Tejútrendszer középpontja körül, egy elliptikus pályán. A Föld kb. 150 millió km-re kering a Naptól, tehát a gravitációja kb. 8,3 perc alatt ér el a Földig. Ez alatt a Nap odébb mozdul az űrben 110.000 km-t, miközben az átmérője 1.392.000 km (ami az elmozdulás 12,654-szerese). Látszólag nem nagy a távolság különbség, ezért is olyan kicsi a Földpálya ellipszise. De a Jupiter például 740 millió km-re van a Naptól, ami a Nap-Föld távolság 4,95-szöröse, míg a Neptunusz 4,536 milliárd km-re van, ami a Nap-Föld távolság 30,32-szerese. Tehát a Neptunuszról nézve a Nap két és fél átmérőnyivel hátrébb látszódik onnan, ahol valójában tartózkodik.

Ha a gravitáció végtelenül gyorsan terjedne, a Nap mindig a pálya fókuszpontjában tartózkodna, így a bolygók nem maradnának le a pillanatnyi helyzetétől és ellipszis helyett körpályákon keringenének körülötte, függetlenül a Nap mozgási sebességétől. Valamennyi pályaperturbáció persze ekkor is fellépne, hisz a bolygók kölcsönösen zavarják egymást a tömegvonzásukkal, de nem alakulnának ki olyan erősen elnyúlt elliptikus pályák, amiket megfigyelhetünk a külső Naprendszerben keringő törpebolygók és üstökösök esetében.

Kepler 2. törvényének magyarázata:

A bolygók azért mozognak gyorsabban a Naphoz közel, illetve lassabban a Naptól távol, mert az ellipszis pályán a Nap felé közeledve a mozgási sebességük összeadódik a Nap vonzóerejével, növelve a sebességüket. A Naptól távolodva viszont a mozgási sebességük kivonódik a Nap vonzóerejéből, csökkentve a sebességüket. Minél közelebb ér a bolygó a Naphoz, annál nagyobb a hatáskeresztmetszete a gravitációja számára, így erősebben hat rá a vonzereje, tehát gyorsítja. Minél távolabb ér a bolygó a Naptól, annál kisebb a hatáskeresztmetszete a gravitációja számára, így gyengébben hat rá a vonzereje, tehát kevésbé gyorsítja. Minden bolygónak van egy adott impulzusmomentuma, aminek megmaradásához - változatlan bolygótömeg esetén - változó sebesség értékekre van szükség. Mivel a bolygók az űr vákuumában mozognak, gyakorlatilag nem hat rájuk súrlódás (az űrlégkör hatása elhanyagolható), így sokáig megőrzik az impulzusmomentumukat, amit csak a többi bolygó, illetve a távoli csillagok gravitációs hatásai befolyásolnak kis mértékben.

Kepler 3. törvényének magyarázata:

Minél távolabb kering egy bolygó a Naptól, annál lassabban mozog körülötte. Ennek oka, hogy kisebb a hatáskeresztmetszete a Nap gravitációja számára, tehát gyengébb a vonzóerő, ami közeledve hozzáadódik a sebességéhez, távolodva kivonódik belőle. A pályán maradáshoz egy adott bolygótömeg esetén adott sebességre van szükség. Ha növeljük a távolságot, csökkenteni kell a sebességet ahhoz, hogy az impulzusmomentum ne változzon. Ha nem csökken a sebesség, nőni fog az impulzusmomentum, ami magasabb pályára viszi az égitestet. Ezért lehet gyorsítással magasabb pályára emelkedni egy égitest körül, lassítással alacsonyabb pályára ereszkedni a gravitációs terében (változatlan tömeg mellett), lásd: árapály hatás.

Ettől eltérően, a csillagok keringési sebessége nem csökken ugyanilyen arányban a galaxis középpontjától távolodva, hanem nagyjából ugyanannyi marad egészen a pereméig, ami a Tejútrendszer esetében kb. 200-240 km/s. Ez látszólag ellentmond Kepler 3. törvényének, de csak azért, mert a csillagászok elfelejtették figyelembe venni azt a tényt, hogy a galaxis magja nem egyetlen égitestből áll, hanem sok égitestből, amik egy nagy kiterjedésű térfogatban mozognak, egymással összhangban. Tehát itt figyelembe kell venni, hogy a galaxismaghoz közel kisebb a csillagokat pályán tartó gravitációs vonzás, attól távolodva viszont nagyobb. Mivel a galaxis peremén keringő csillagokat nem csak a galaxis magja vonzza, hanem a mag körül (a korongban) keringő összes csillag együttes gravitációja. Ez pedig képes ellensúlyozni a gravitációs erő távolsággal négyzetes arányban történő csökkenését.

4. ÁRAPÁLY HATÁS

Minden bolygó körül található egy rá jellemző, egyedi stacionárius pályamagasság az egyenlítő fölött, amin a körülötte keringő holdak pontosan olyan sebességgel keringenek, hogy a bolygó felszínéről nézve (nagyjából) mindig ugyanott látszódnak az égen. Ilyenkor az árapály hatás állandósul, tehát a bolygó légkörét, vizét és kőzetanyagát ugyanarra a helyre húzza a hold gravitációs tere. A stacionárius pályamagasság függ a bolygó tömegétől, ami meghatározza a gravitációs terét, valamint a forgási sebességétől, ami meghatározza a gravitációs térben azt a távolságot, ahol a keringési sebesség pont akkora, hogy a keringési idő azonos legyen a bolygó forgásidejével. A Föld esetén a geostacionárius pályamagasság 35.786 kilométer magasan húzódik az átlagos tengerszint fölött, ahol a keringési sebesség: 3,07 km/s, a keringési idő pedig: 1436 perc (egy sziderikus nap).

Ha a hold alacsonyabban kering, mint a stacionárius pályamagasság, akkor gyorsabb lesz a bolygó forgásánál, tehát megelőzi a felszínét: hamarább végez egy keringést, mint egy nap a bolygón. Ilyenkor az árapály hatás előrefelé siet a bolygón, követni próbálva a holdat, azaz gyorsítja a bolygó forgását, előrehúzva annak anyagát. Ugyanakkor a bolygó meg lassítja a holdat, visszahúzva annak anyagát, amitől az egyre alacsonyabb pályára kerül. Lényegében befelé spirálozik körülötte, amíg le nem zuhan a felszínére. Vagy a Roche-határt elérve szét nem szakad az anyaga az árapály hatás miatt, mert a bolygó felöli oldalát nagyobb vonzás éri, mint a távolabbi oldalát, mechanikus feszültséget keltve az anyagában. A Roche-határ helye függ a hold szakítószilárdságától (anyagi összetételétől), azaz a deformálhatóságának függvénye.

Ha a hold magasabban kering, mint a stacionárius pályamagasság, akkor lassabb lesz a bolygó forgásánál, tehát lemarad a felszínéhez képest: tovább végez egy keringést, mint egy nap a bolygón. Ilyenkor az árapály hatás hátrafelé késik a bolygón, követni próbálva a holdat, azaz lassítja a bolygó forgását, hátrahúzva annak anyagát. Ugyanakkor a bolygó meg gyorsítja a holdat, előrehúzva annak anyagát, amitől az egyre magasabb pályára kerül. Lényegében kifelé spirálozik körülötte, amíg el nem szakad tőle és kirepül az űrbe. A Hold például évente 3,8 centiméterrel kerül messzebb a Földtől, aminek forgása a Hold fékező ereje miatt évente 0,029 másodperccel lassul. Így nagyjából 1,6 milliárd év múlva egy földi nap a mai 55-szöröse lesz és a Hold is ennyi idő alatt kerüli meg a Földet. Tehát az árapály fékező hatása miatt a geostacionárius pálya gyorsabban fog egyre magasabbra emelkedni, mint ahogy a Hold távolodik tőlünk. Amikor a Holdat eléri a geostacionárius pályamagasság, a távolodása megáll, így valószínűleg sosem fog elszakadni tőlünk, egészen addig, míg a Nap vörös óriássá válva be nem kebelezi mindkét égitestet.

Ebből következik, hogy a holdak többnyire nem keringenek örökké a bolygójuk körül. Idővel vagy rájuk zuhannak vagy elszakadnak tőlük, néha megrekednek a stacionárius pályamagasságon, amíg valami (egy beléjük csapódó meteor) odébb nem löki őket. Ugyanígy a bolygók keringése is változik a csillaguk körül. A csillag a közeli bolygóit idővel elnyeli, a távolabbiakat pedig elveszíti. A gyakorlatban ezt módosítják a tömegváltozások. A csillagok sugárzása folyamatos fény és anyagveszteséggel jár a számukra, ugyanakkor a beléjük zuhanó üstökösök és bolygók növelik a tömegüket. A belsejükben zajló fizikai folyamatok új fénykvantumok és ezekből új anyagi részecskék megteremtődését idézik elő, ami növeli a tömegüket valamilyen ütemben. A bolygók felszínére lezuhanó holdak, meteorok, űrtörmelékek és a befogott napszél növelik a tömegüket. Az erősebb becsapódások robbanásai az anyaguk egy részének kilökődésével járnak az űrbe, ami később vagy visszahullik rájuk vagy elszakad tőlük. A napszél folyamatosan lesodorja róluk a felső légkörüket, s annak illékony, könnyű elemeit (hidrogén, hélium). Amit vagy vissza tudnak tartani a gravitációjukkal vagy elveszítik; hosszú csóva formájában leszakad róluk az űrbe.

A bolygóknak nem csak a tömegük, de a keringési sebességük is megváltozik időnként. Egyrészt gyorsítják őket a belső bolygók, másrészt lassítják őket a külső bolygók az árapály hatásukkal. Továbbá a beléjük csapódó meteorok és holdak ütközései meglökik őket, átadva nekik az impulzusmomentumukat. Ennek irányától függően gyorsulnak vagy lassulnak a pályájukon. Ha a bolygórendszer közelében elhalad egy másik csillag vagy egy szabadon kóborló bolygó, a gravitációjával az is befolyásolja a bolygók és holdak sebességét, s ennélfogva megváltoztatja pályájukat. Az egész egy dinamikusan visszacsatolt rendszer, aminek mozgása attraktorszerűen változik, sosem marad ugyanolyan. Ezért ezek mind ideiglenes rendszerek, amik élettartama korlátozott még a legjobb esetben is. Csak emberi időléptékben tűnnek állandónak és változatlannak, a kozmikus időskálán mérve folyamatosan változóak.

5. AJÁNLOTT CIKKEK

1. A Kepler törvények részletes ismertetése:
https://www.netfizika.hu/tudas/node/15003

2. Merre mozog a Föld az univerzumban?
https://bigthink.com/starts-with-a-bang/earth-move-universe/

3. A geostacionárius pálya:
https://hu.wikipedia.org/wiki/Geostacion%C3%A1rius_p%C3%A1lya

4. A Roche-határ:
https://hu.wikipedia.org/wiki/Roche-hat%C3%A1r

5. A Tejútrendszer forgása:
https://www.csillagaszat.hu/tudastar/a-tejutrendszer/03-a-tejutrendszer-forgasa/

Készült: 2024.02.06. - 03.21.

Vissza a tartalomhoz