N DIMENZIÓS MÁTRIXOK BEJÁRÁSI ÚTVONALAI

1. ELŐSZÓ

Az alábbiak megértéséhez érdemes elolvasni a Merőlegesség n dimenzióban (2007, matematika) című írást, továbbá ajánlott ismerni a matematikai mátrixok főbb tulajdonságait. Ajánlott forrás: https://hu.wikipedia.org/wiki/M%C3%A1trix_(matematika)

A matematikai mátrix olyan elemek táblázata, amik lehetnek számok, kifejezések, függvények. Sokféle alkalmazásuk van, amivel a lineáris algebra foglalkozik. A síkmátrixok m sorból és n oszlopból állnak. A mátrix dimenziói csak pozitív egész számok lehetnek. Az informatikában a síkmátrixokat két dimenziós tömbnek nevezik. A tömb elemei indexeléssel vannak összekapcsolva, aminek szerkezetétől függ, hogyan tud a felhasználó vagy a program eljutni egy megadott elemtől egy másikig?

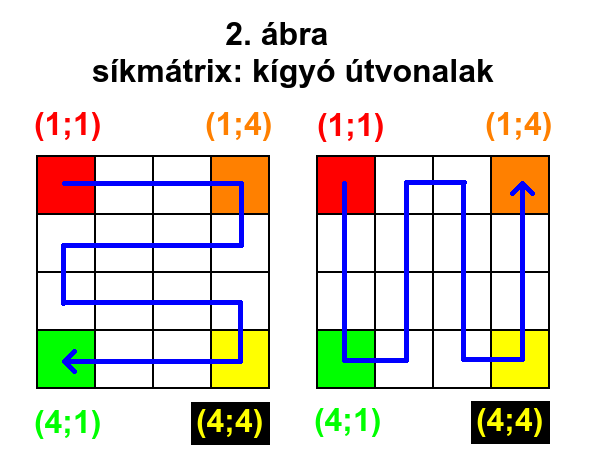
A legegyszerűbb síkmátrix bejárási útvonalak (beírások és kiolvasások) azok, amik az élekkel párhuzamosan haladnak végig a sorokon, oszlopokon, az első elemtől az utolsóig. Ezeknek három fő fajtája van: A fésű útvonal egy sor vagy oszlop végére érve visszaugrik az elejére és továbblép a következő sorra vagy oszlopra (1. ábra). A kígyó útvonal oda-vissza kanyarogva halad sorról sorra vagy oszlopról oszlopra (2. ábra). A csiga útvonal spirálisan befelé vagy kifelé csavarodva, balra vagy jobbra halad végig az elemeken (3. ábra). Ezek tulajdonságaival külön fejezetekben foglalkozunk.

Az alábbiakban azt mutatom be, hogy lehet kiszámolni az m elemű élhosszúsággal rendelkező, n dimenziós mátrixok különböző bejárási útvonalainak számát, amik mentén sorra vehető az összes elem az elsőtől az utolsóig? Az elemek dimenziószáma a könnyebb kezelhetőség érdekében mindig megegyezik a mátrix dimenziószámával, tehát 1D-s szakasz esetén 1D-s, 2D-s négyzet esetén 2D-s, 3D-s kocka esetén 3D-s, stb. Ezen útvonalak ismeretére a gyakorlatban sok helyen van szükség. Az informatikában például a kereszt paritásos ellenőrző kódok előállításánál, amikkel korlátozott mértékben észrevehetők és kijavíthatók a valószínűbb hibák. A két vagy három dimenziós kijelzőkre kimenő, illetve a két vagy három dimenziós letapogatóktól bejövő adatfolyamok feldolgozásakor szintén fontos kiválasztani a megfelelő bejárási útvonalat a lehetségesek közül. De egyes titkosító algoritmusok is mátrix alapú bitkeverést használnak az üzenetek gyors és hatékony titkosításához.

2. FÉSŰ ÚTVONALAK

Egy 1D-s szakasz sora kétféle útvonalon haladva járható végig:
A->B: balról jobbra.
B->A: jobbról balra.
Mivel két végpontja van. Az egyikből elindulunk, a másikba megérkezünk.

Egy 2D-s négyzetes síkmátrixnak 4 sarka (csúcspontja) van (ABCD), így az útvonalak:
A->B->C->D: soronként balról jobbra, fentről lefelé.
A->C->B->D: oszloponként fentről lefelé, balról jobbra.
B->A->D->C: soronként jobbról balra, fentről lefelé.
B->D->A->C: oszloponként fentről lefelé, jobbról balra.
C->D->A->B: soronként balról jobbra, lentről felfelé.
C->A->D->B: oszloponként lentről felfelé, balról jobbra.
D->C->B->A: soronként jobbról balra, lentről felfelé.
D->B->C->A: oszloponként lentről felfelé, jobbról balra.

Mivel minden csúcspontból két irányba lehet elindulni, a két kifutó éllel párhuzamosan (1. ábra). Ez összesen 8 lehetséges útvonal, amik páronként ellentétes irányúak egymással. Ez nem ismétlés nélküli permutáció (n!), mert körbejárásokat (csiga útvonalat) nem végzünk.

Egy 3D-s kocka térmátrixnak 8 sarka (csúcspontja) van (ABCDEFGH: 4. ábra), így az A-ból kiinduló és a G-be megérkező útvonalak:
Az ABCD lappal kezdve:
A->B->D->C->...->E->F->H->G: az első síkmátrixtól párhuzamosan a hátsó síkmátrixig.
A->D->B->C->...->E->H->F->G: az első síkmátrixtól párhuzamosan a hátsó síkmátrixig.
Az ABFE lappal kezdve:
A->B->E->F->...->D->C->H->G: a felső síkmátrixtól párhuzamosan az alsó síkmátrixig.
A->C->E->G->B->D->F->H: a felső síkmátrixtól párhuzamosan az alsó síkmátrixig.
Az AEHD lappal kezdve:
A->E->D->H->...->B->F->C->G: a bal oldali síkmátrixtól párhuzamosan a jobb oldali síkmátrixig.
A->D->E->H->...->B->C->F->G: a bal oldali síkmátrixtól párhuzamosan a jobb oldali síkmátrixig.

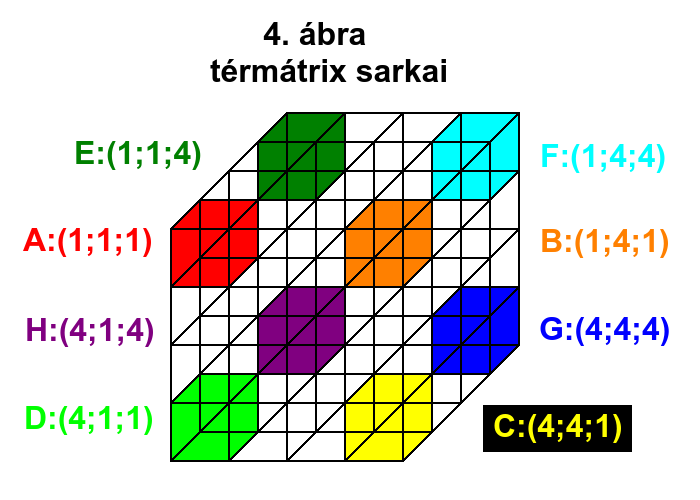
Mivel minden csúcspontból három irányba lehet elindulni, a három kifutó éllel párhuzamosan, majd minden irányból a két szomszédos lap felé lehet továbbhaladni, ez 6 útvonalat jelent, ami összesen: 6x8=48 útvonal. Ebből következik, hogy az mxmxm elemszámú kocka lényegében mxm elemszámú négyzetekből (valójában: kockák négyzetes hasábjából, mivel az elemek térdimenziószáma azonos a mátrixéval) áll, amikből m darab található egymás mögött. Az elemekhez hozzárendelt sorszámok megfeleltethetők az XYZ koordinátarendszer pontjainak, amennyiben az (1;1;1) pontból indulunk el.

Egy 4D-s hiperkocka túltérmátrixnak 16 sarka (csúcspontja) van és minden csúcspontból négy irányba lehet elindulni, a négy kifutó éllel párhuzamosan, majd minden irányból a három szomszédos lap felé lehet továbbhaladni, ahonnét két szomszédos térfogat felé lehet továbbhaladni. Ez 24 útvonalat jelent, ami összesen: 16x4x3x2=384. Ebből következik, hogy az mxmxmxm elemszámú hiperkocka lényegében mxmxm elemszámú kockákból (valójában: hiperkockák kockás hasábjából) áll, amikből m darab található egymás mögött. A 4D-s elemek azonosítója négy számból áll: (0;0;0;0). Ez a szabály a felsőbb térdimenziókra is érvényes.

A 2D-s és 3D-s mátrixok alapján meghatározható a fésű útvonalak kiszámításának képlete:
Térdimenzió száma: n.
Csúcsok száma: c.
Egy csúcsból kifutó élek száma: e.
Egy élből kifutó oldallapok száma: l.
Egy oldallapból kifutó térfogatok száma: t.
Egy térfogatból kifutó túltérfogatok száma: h.
Egy túltérfogatból kifutó kültérfogatok száma: k.
Egy kültérfogatból kifutó feltérfogatok száma: f.
A fésű útvonalak száma: F.
Képlet: cxexlxtxh=F
Ahol: n,c,e,l,t,h,k,f,F=Nˇ1 (pozitív egész számok)

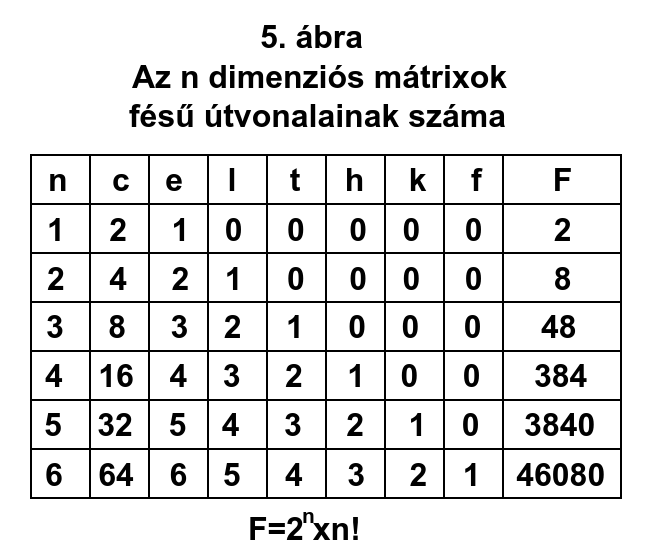
Ha n=1, akkor c=2, e=1, l=0, tehát: 2x1=2.
Ha n=2, akkor c=4, e=2, l=1, t=0, tehát: 4x2x1=8.
Ha n=3, akkor c=8, e=3, l=2, t=1, h=0, tehát: 8x3x2x1=48.
Ha n=4, akkor c=16, e=4, l=3, t=2, h=1, k=0 tehát: 16x4x3x2x1=384.
Ha n=5, akkor c=32, e=5, l=4, t=3, h=2, k=1, f=0, tehát: 32x5x4x3x2x1=3840.
Ha n=6, akkor c=64, e=6, l=5, t=4, h=3, k=2, f=1, tehát: 64x6x5x4x3x2x1=46.080.

Ebből a sorozatból (5. ábra) már látszik a kirajzolódó, n térdimenziós képlet: F=2^nxn!

3. KÍGYÓ ÚTVONALAK

A kígyó útvonal lényegében ugyanaz, mint a fésű, azzal a különbséggel, hogy minden második (páros számú) sor vagy oszlop kiolvasása fordított irányban történik (2. ábra); visszafelé. Ennélfogva, ha a síkmátrix élhosszúsága (m) páros számú, akkor az utolsó elem az elsőhöz képest élszomszéd lesz, ha viszont páratlan számú, akkor nem (a négyzet átló túlvégére esik). Ez nem változtatja meg az útvonalak számát, így az n térdimenziós képlete azonos lesz a fésűével: K=2^nxn!
A kígyó útvonalak száma: K.

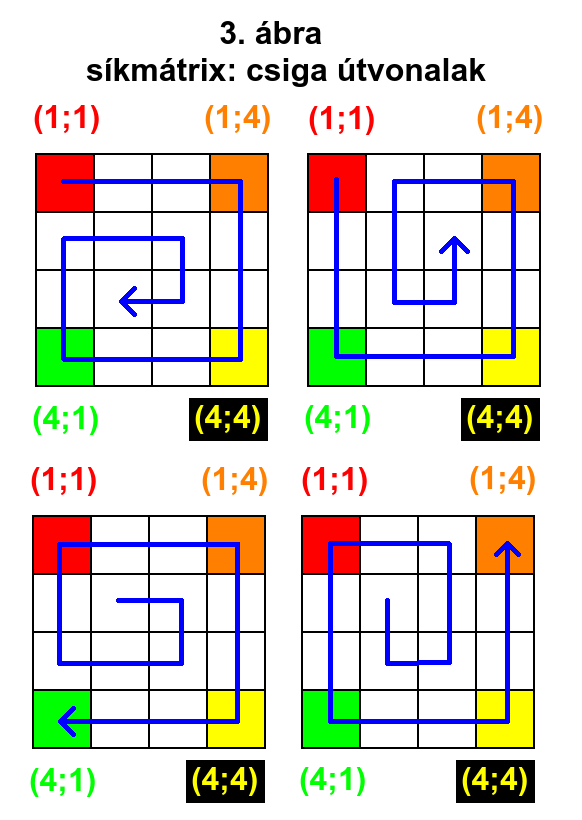
4. CSIGA ÚTVONALAK

A csiga útvonalak egy síkmátrixban 4x4=16 félék lehetnek (3. ábra). Kintről befelé haladók: a 4 sarokból a középső elemig balról jobbra vagy jobbról balra kanyarodva, összesen: 8 féleképp. Bentről kifelé haladók: a középső elemtől valamelyik sarokig balról jobbra vagy jobbról balra kanyarodva. Ha a síkmátrix élhosszúsága (m) páros számú, akkor a középső elem változó: valamelyik a 4 középen lévő elem közül, amik mindegyikéből 2 irányba lehet elindulni kifelé, összesen: 8 féleképp. Bentről kifelé haladva bármelyiket választhatjuk. Ha viszont páratlan számú, akkor 1 középső elem van, amiből 4 irányba lehet elindulni kifelé és mindegyik szomszédos elemből két irányba lehet továbbhaladni, összesen: 8 féleképp.

A térmátrixban lapról lapra haladva összesen 6 irányban lehet végighaladni a kockán, így az útvonalak száma: 16x6=96. Ez kétszerese a fésű útvonalaknak, amiből következik az n térdimenziós képlet: C=2^nxn!x2
A csiga útvonalak száma: C.

A csiga útvonalak használatának azonban komoly hátránya, hogy kintről befelé egyre rövidülnek a kiolvasott sorok/oszlopok, bentről kifelé pedig egyre hosszabbodnak, tehát változó a szakaszok hossza, amit külön figyelembe kell venni a szoftveres megvalósításkor, hogy ne történjen többszörös kiolvasás egyes elemeknél.

5. KEVERT ÚTVONALAK

Ha egy nagyobb számsorból több mátrixot képzünk, lehetőségünk van keverni egymással a különböző bejárási útvonalakat, minden mátrixon másikat alkalmazva. Egyrészt a három fő fajtán belül, másrészt a fajták között. Minden térdimenziószinten, ami sokszorosára növeli az útvonalak számát. Például: síkmátrix esetén a 8 féle fésű útvonal 8x8=64 féleképp keverhető kettesével, 8^3=512 féleképp keverhető hármasával, valamint 8^8=16.777.216 féleképp nyolcasával. Térmátrix esetén a 48 féle fésű útvonal 48x48=2304 féleképp keverhető kettesével, a 48^48 pedig olyan nagy szám, hogy csak lebegőpontosan ábrázolható (5x10^80). Ha pedig a mátrixok élhosszúságát is variáljuk egy adott tartományban (pl.: 4<=m<=16 vagy 4<=m<=64), illetve nem csak négyzetes és kocka mátrixokat használunk, hanem téglalap és téglatest alakúakat is (mxn, illetve mxnxo élhosszúságokkal), még tovább növelhetjük a lehetőségek számát.

A kevert útvonalak értelmezhetők úgy is, mintha az egyes mátrixokat egymáshoz képest adott szöggel elforgatnánk vagy a térmátrixokon belüli egyes síkmátrix négyzetes hasábokat egymáshoz képest adott szöggel elforgatnánk; balra vagy jobbra 90 fokkal vagy 180 fokkal. És ezek az elforgatások is kombinálhatók egymással sokféleképpen. Például: balra 90 fokkal: B, jobbra 90 fokkal: J, 180 fokos félfordulat: F.
1. BBBB.
2. JJJJ.
3. BBJJ.
4. JJBB.
5. BJBJ.
6. JBJB.
7. BBJBBJ.
8. JJBJJB.
9. FF.
10. BFB.
11. JFJ.
12. BBF.
13. JJF.
14. FBJ.
15. FJB.
16. BBBF.
17. JJJF.
stb.

6. ALKALMAZÁSOK

Amennyiben titkosításra használjuk a mátrixokat, a kiolvasási sorrend nem lehet azonos a beolvasási sorrenddel, sem annak ellenkező irányú párjával, mert akkor nem történik bitkeverés. A bitkeverés bonyolultsága tovább fokozható, ha több lépésben egymás után megismételjük a folyamatot, eltérő mátrix élhosszúságokkal és útvonalakkal, mert ezáltal az egyes blokkok átfedik egymást és a tartalmuk összekeveredik. Mivel a titkosítani szándékozott üzenet hossza többnyire nem egyezik meg a használt mátrixok elemszámának egész számú többszörösével, ki kell egészíteni további elemekkel, amik értékét célszerű véletlenszerűen megválasztani. Ezeket valamilyen (kódolásonként változó) arányban érdemes egyrészt az üzenet elejére, másrészt a végére beszúrni. Ahhoz, hogy a kód feltörését még jobban megnehezítsük, annyi véletlenszerű elemet kell az üzenet elejéhez és végéhez hozzáadni, hogy legalább egy mátrixot kitöltsenek. Ekkor, ha a kódtörő rendszernek sikerül is megtalálnia a helyes kódot, az első (vagy utolsó) mátrix dekódolt tartalma akkor is egy zagyvaság lesz, vagyis nem tudhatja, hogy helyes-e a kód? Ez csak a következő mátrix dekódolásakor derül ki, ami további jelentős időnövekedéssel jár, mert minden lehetőségen végig kell próbálnia minden lehetőséget. Ha középen kezdi a kódtörést, akkor ugyanezen akadályt kell leküzdenie, mert nem tudja, hová esik pontosan az adott mátrix eleje?

A fentiekből következik, hogy jól megválasztott paraméterekkel gyakorlatilag feltörhetetlen bitkeverő blokktitkosítást hozhatunk létre, kellően nagy számsorokon, amiket se a ma létező legnagyobb szuperszámítógépek, se a közeljövőben elméletileg elképzelhető legnagyobb szuperszámítógépek, de még a kvantumszámítógépek sem fognak tudni soha feltörni, emberileg ésszerű időtartam (1-2 emberöltő) alatt. Ezért használják ezt a módszert a ma használatos szimmetrikus kulcsú rejtjelezések is, mint a DES, 3DES, AES, amik emellett még további trükkös módszereket is tartalmaznak az üzenetek titkosítása céljából. Ezek nyilvánosságra hozott tulajdonságairól itt olvashattok többet:
1. Szimmetrikus kulcsú rejtjelezés: https://hu.wikipedia.org/wiki/Szimmetrikus_kulcs%C3%BA_rejtjelez%C3%A9s
2. Advanced Encryption Standard: https://hu.wikipedia.org/wiki/Advanced_Encryption_Standard
3. DES titkosítás és visszafejtés online: https://des.codethoi.com/hu/

Készült: 2024.07.18. - 26.

Vissza a tartalomhoz