SZOMSZÉDOS KÖRÖK SZÁMA SÍKBAN

Az alábbiak megértéséhez feltétlenül el kell olvasni a: Szomszédos körök n dimenzióban (2023, matematika) című írást.

1. KÖRÖK ÉS SZOMSZÉDAIK

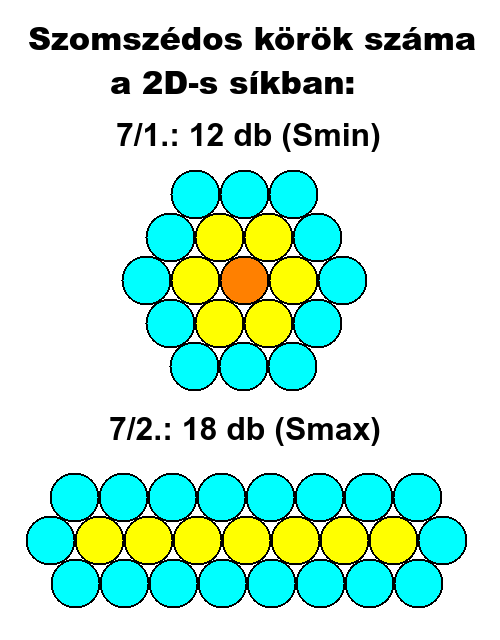
Több, egymással legalább egy pontban érintkező kör K halmaza (sárga) többféleképp elrendezhető a síkban geometriailag. Ezért a K halmaz köreivel legalább egy pontban érintkező, szomszédos körök (K-t körbevevő) S halmazának (világoskék) darabszáma is többféle lehet. S halmaz köreinek legalább egy pontban érintkezniük kell egymással. Ez alól kivételt csak az egy körből álló lyukak képeznek a K halmaz belsejében. Az alábbi ábrákon a K+S=E halmaz lehetséges, egyedi formái láthatók. Egyedi formák azok, amik forgatással és tükrözéssel nem vihetők át egymásba. K elemeinek száma: 1-től 7-ig terjed.

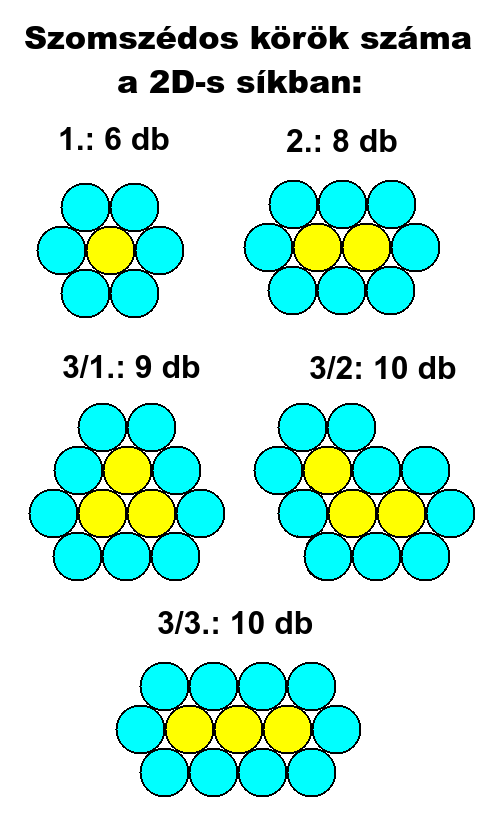
Ezek alapján:
Ha K=1, akkor S=6, E=7.
Ha K=2, akkor S=8, E=10.
Ha K=3, akkor S=9, 10, Emin=12, Emax=13.
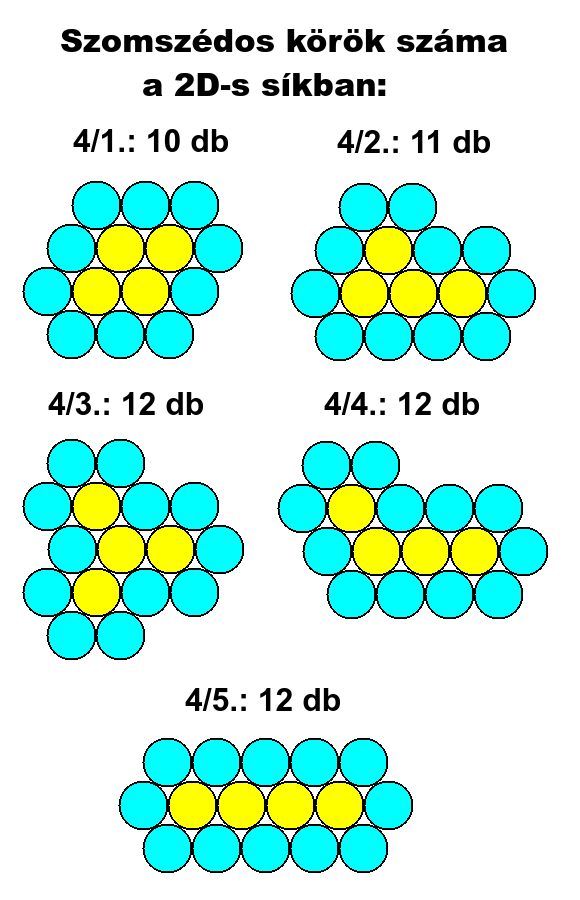
Ha K=4, akkor S=10, 11, 12, Emin=14, Emax=16.
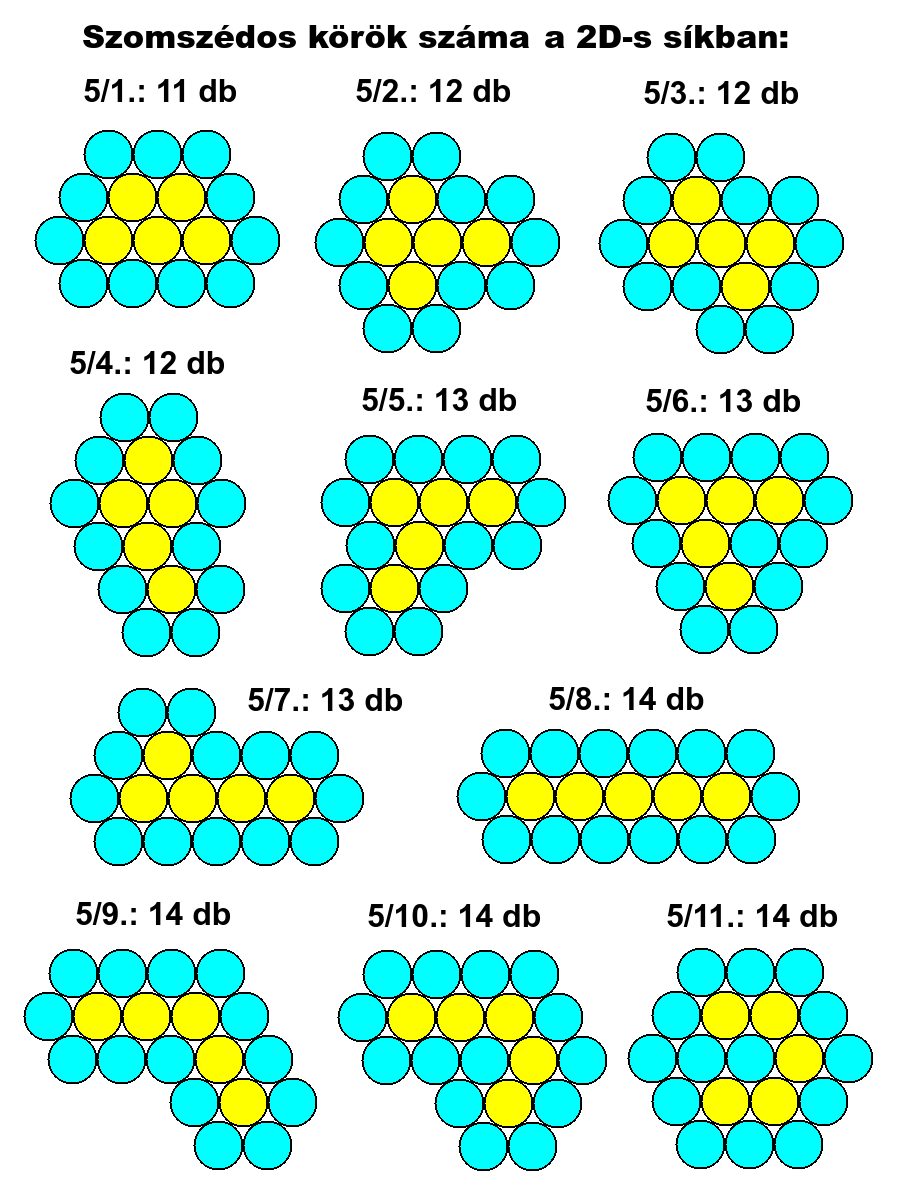
Ha K=5, akkor S=11, 12, 13, 14, Emin=16, Emax=19.
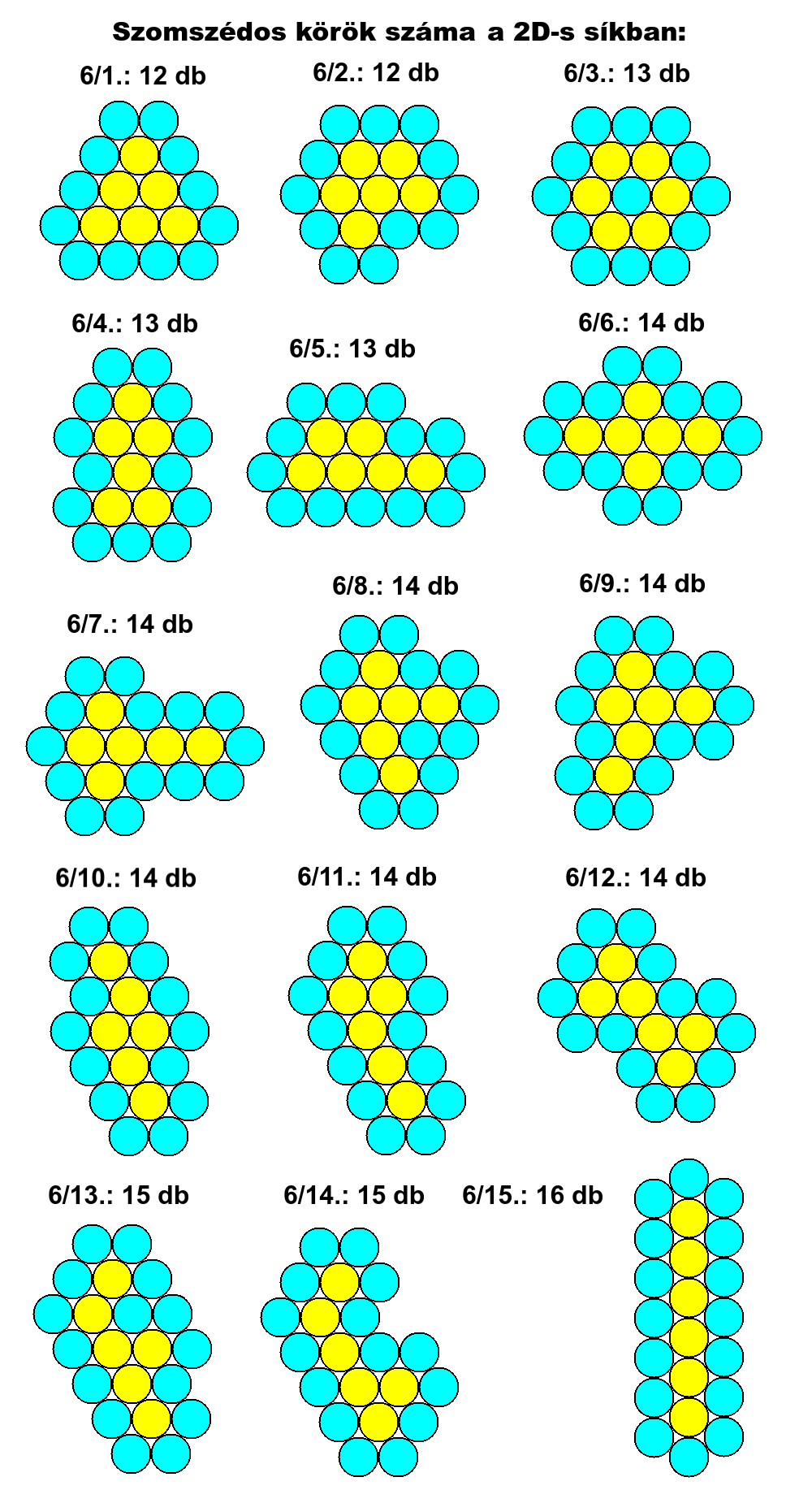
Ha K=6, akkor S=12, 13, 14, 15, 16, Emin=18, Emax=22.
Ha K=7, akkor S=13, 14, 15, 16, 17, 18, Emin=20, Emax=25.

A sorozat alapján a következő összefüggések állapíthatók meg (n: természetes szám):
1. K halmaz elemei egymással való érintkezésének értéke: 0<=Ké<=6. K=1 esetén Ké=0. K=7-től kezdve lehet Ké=6, ekkor a kör színe: narancs.
2. S halmaz elemei egymással való érintkezésének értéke: 0<=Sé<=5. K=6 esetén lehet Sé=0, ha S2 a K gyűrűn belüli egy körös lyukban található. K=5 esetén lehet Sé=5, ha S=14.
3. K halmaz elemeinek S halmaz elemeivel való érintkezésének értéke: 0<=KSé<=6. K=7-től kezdve lehet KSé=0. K=1 esetén KSé=6.
4. S halmaz elemeinek K halmaz elemeivel való érintkezésének értéke: 1<=SKé<=6. K=5-től kezdve lehet SKé=1. K=6 esetén SKé=6, ha S2 a K gyűrűn belüli egy körös lyukban található.
5. Ha K=n és n>1, akkor S legkisebb értéke: Smin=n+6.
6. Mivel S nem értelmezhető K nélkül, K=1 esetén Smin=6.
7. Ha K=n, akkor S legnagyobb értéke: Smax=2xn+4 (azaz: (n+6)+(n-2)).
8. Ha K=n és n>1, akkor S lehetséges elemeinek száma: Se=n-1.
9. Mivel K+Smin=Emin, ha K=n és n>1, akkor (Emin)ˇn=((Emin)ˇn-1)+2. Emin: páros szám.
10. Mivel K+Smax=Emax, ha K=n, akkor (Emax)ˇn=((Emax)ˇn-1)+3. Ha K: páros szám, akkor Emax is, különben mindkettő páratlan.
11. Ahogy nő K elemszáma, egyre több formába rendezhető. Így az egyes S értékek is több formába rendeződhetnek, amik képletei még nem ismertek. K=7-nél már olyan sok forma van, hogy csak az Smin és Smax formákat ábrázoltam.
12. Kellően nagy K halmaz esetén létrehozhatók olyan geometriák, amik peremén körben öblök találhatók, ahová S elemei félszigetszerűen betüremkednek. Ez teszi lehetővé a betüremkedés méretétől és formájától függően az Sé=1, 3, 4, 5 értékeket.
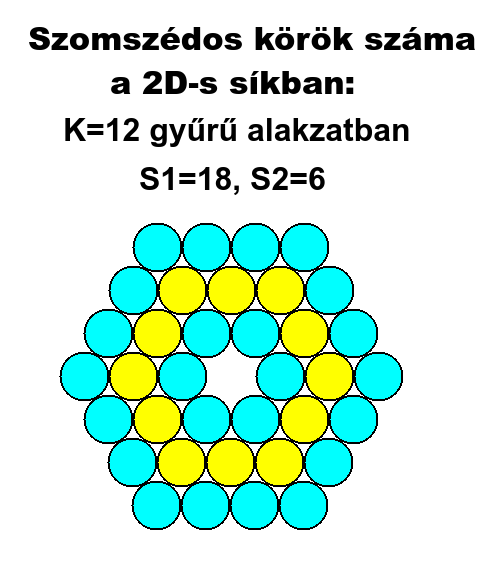
13. Kellően nagy K halmaz esetén létrehozhatók olyan geometriák is, amik S-t két vagy több, egymással nem érintkező részhalmazra bontják. Ezeket S1, S2, S3, stb. sorszámokkal jelölhetjük. S részhalmazai közül az egyik (S1) K külső szomszédjaiból, a többi (S2, S3, stb.) K belső szomszédjaiból áll, amik K üregeinek (belső lyukak) felszínét borítják. Ezekkel a méretük és bonyolultságuk miatt egyelőre nem foglalkozunk.

2. K RÉSZHALMAZAI

A K halmaz döntően kétféle részhalmazból állhat: egy vagy több csomóból (C halmazok) és/vagy egy vagy több láncból (L halmazok).
1. C részhalmaz elemei egymásal való érintkezésének értéke: 2<=Cé<=6.
2. L részhalmaz elemei egymással való érintkezésének értéke: 1<=Lé<=3.

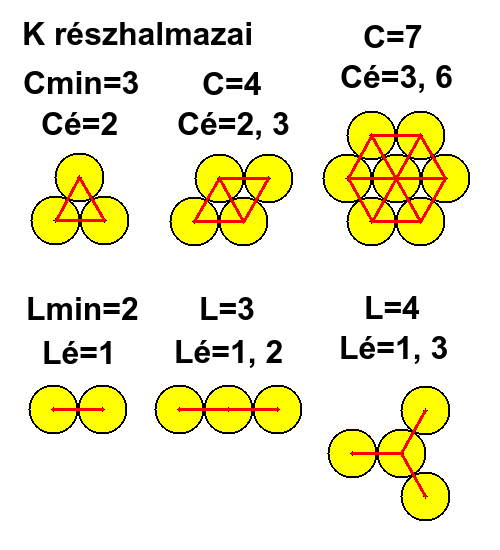
Következmények:
1. Ha 3 elem egymással szomszédos, már csomót alkotnak, így C halmaz legkisebb értéke: Cmin=3.
2. Ha 1 elemnek 3 szomszédja van, amik egymással nem szomszédosak, akkor az L része és egy elágazó lánc elágazási pontja.
3. Ha 2 elem egymással szomszédos, már láncot alkotnak, így L halmaz legkisebb értéke: Lmin=2.
4. Ha K=C, akkor S=Smin.
5. Ha K=L és L egyenes, akkor S=Smax.

3. S RÉSZHALMAZAI

Az S halmaz szintén kétféle részhalmazból állhat: egy vagy több csomóból (B halmazok) és/vagy egy vagy több láncból (D halmazok).
1. B részhalmaz elemei egymással való érintkezésének értéke: 2<=Bé<=5.
2. D részhalmaz elemei egymással való érintkezésének értéke: 1<=Dé<=3.

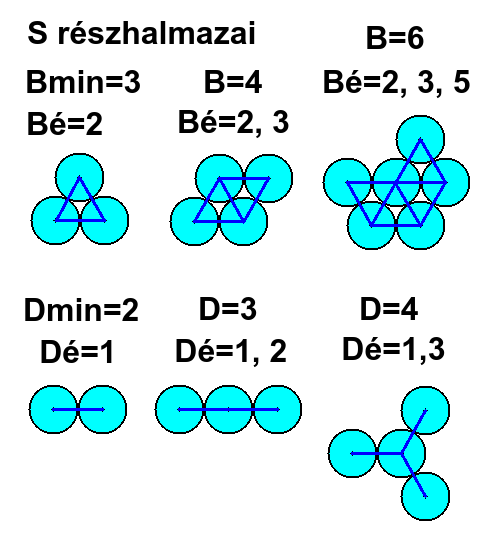
Következmények:
1. Ha 3 elem egymással szomszédos, már csomót alkotnak, így B halmaz legkisebb értéke: Bmin=3.
2. Ha 1 elemnek 3 szomszédja van, amik egymással nem szomszédosak, akkor az D része és egy elágazó lánc elágazási pontja.
3. Ha 2 elem egymással szomszédos, már láncot alkotnak, így D halmaz legkisebb értéke: Dmin=2.
4. Ha S=1 egy K gyűrűben, akkor az elemnek 0 szomszédja van és S nem bontható fel B és D részhalmazokra.
5. Ha S=2 egy K gyűrűben, akkor a két elemnek 1-1 szomszédja van, vagyis S=D.
6. Ha S=3 egy K gyűrűben, akkor S=B (minden elemnek 2 szomszédja van) vagy S=D (két elemnek 1-1, egy elemnek 2 szomszédja van).

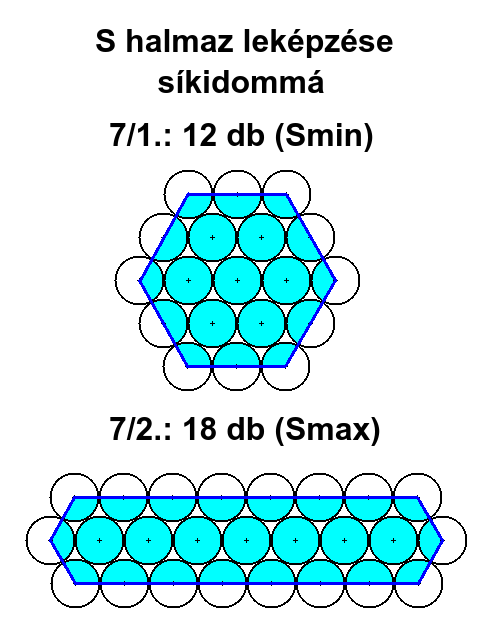
4. S HALMAZ LEKÉPZÉSE SÍKIDOMMÁ

Amint az ábrákon látható, a K halmaz formája megszabja az S halmaz formáját, ami hozzá igazodik. Ha K halmaz növekedése aszimmetrikus, a deformációja több réteggel való beburkolás után is megmarad, nem tűnik el. A K+S=E halmaz egésze leképezhető síkidommá, az S elemei origóinak, mint csúcspontoknak szakaszokkal való összekötésével (kék vonallal). Az így kapott sokszögek (a körök belső részei világoskékkel színezve) lehetnek konvexek vagy nem konvexek. Az E halmaz növelése további rétegekkel nem tünteti el a síkidomok konkáv részeit, de a relatív méretüket csökkenti a halmaz egészéhez viszonyítva.

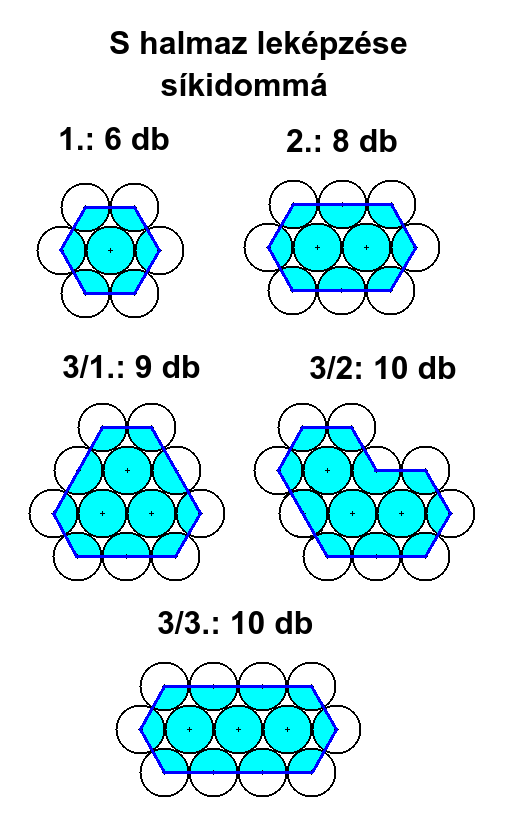
Síkidom azonosítószáma / csúcsainak száma / oldalainak élhosszúsága
(Az élhossz számítása a bal felső sarokban lévő csúcsból indul órairányban. Az élhossz<=S a betüremkedések miatt, amik száma T-vel jelölve.)
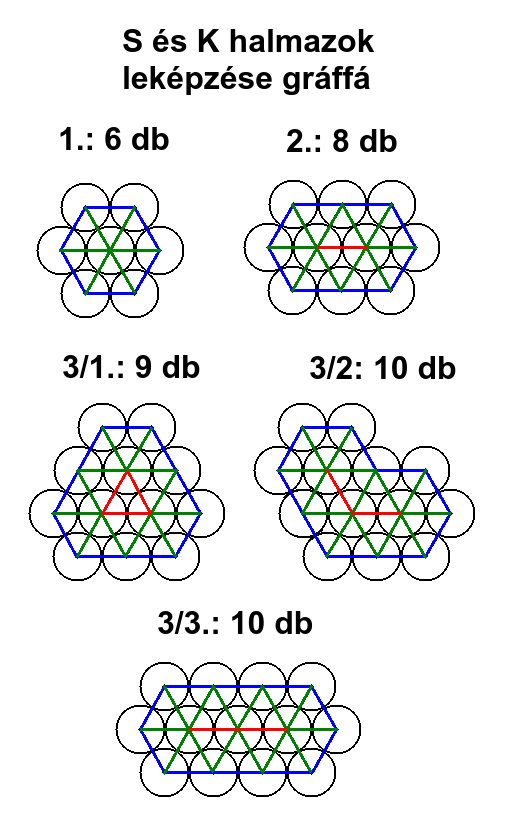
1. / 6 / 1+1+1+1+1+1=6
2. / 6 / 2+1+1+2+1+1=8
3/1. / 6 / 1+2+1+2+1+2=9
3/2. / 8 / 1+1+1+1+1+2+2+1=10
3/3. / 6 / 3+1+1+3+1+1=10
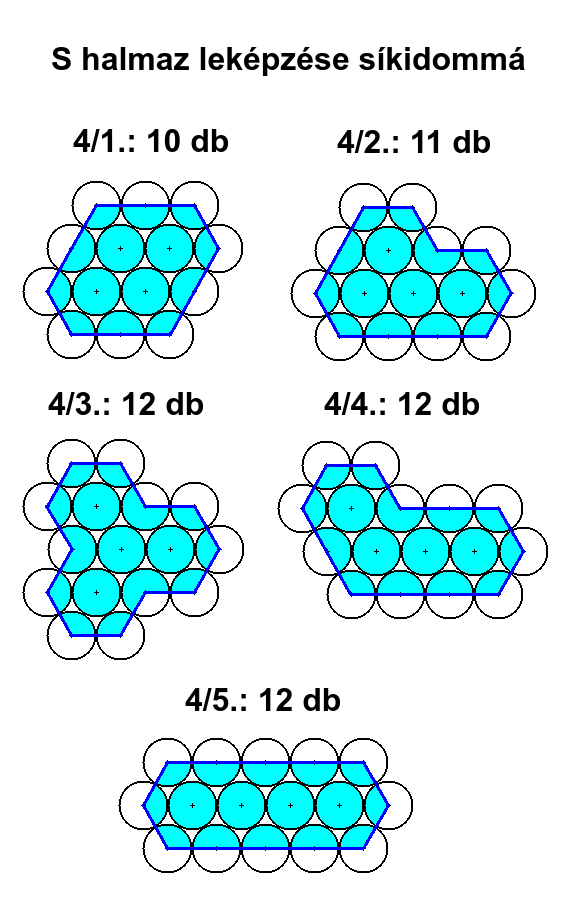
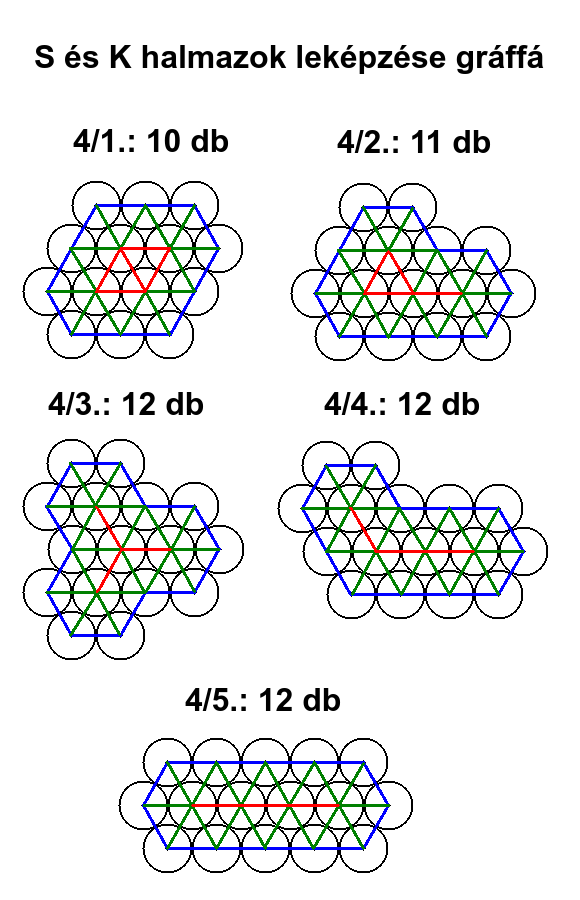
4/1. / 6 / 2+1+2+2+1+2=10
4/2. / 8 / 1+1+1+1+1+3+1+2=11
4/3. / 12 / 1+1+1+1+1+1+1+1+1+1+1+1=12
4/4. / 8 / 1+1+2+1+1+3+2+1=12
4/5. / 6 / 4+1+1+4+1+1=12
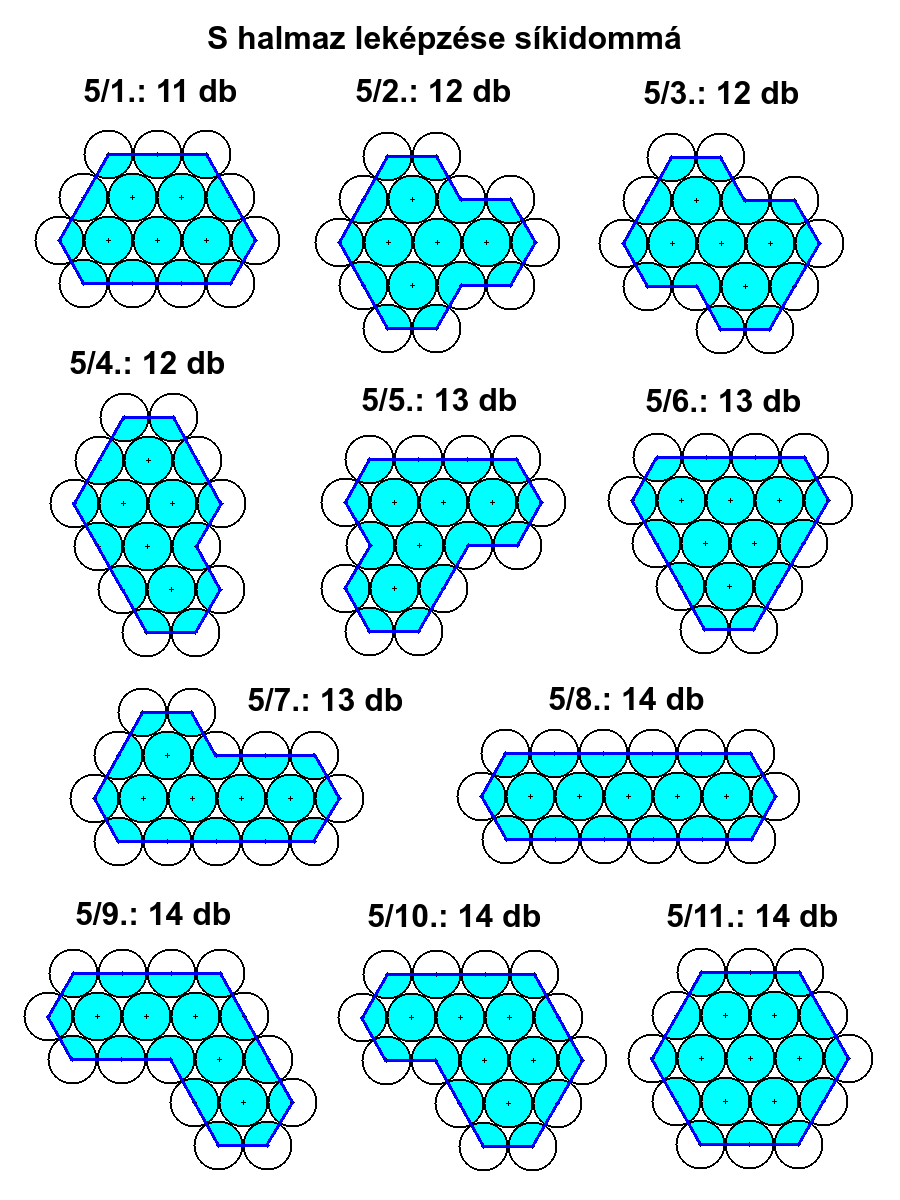
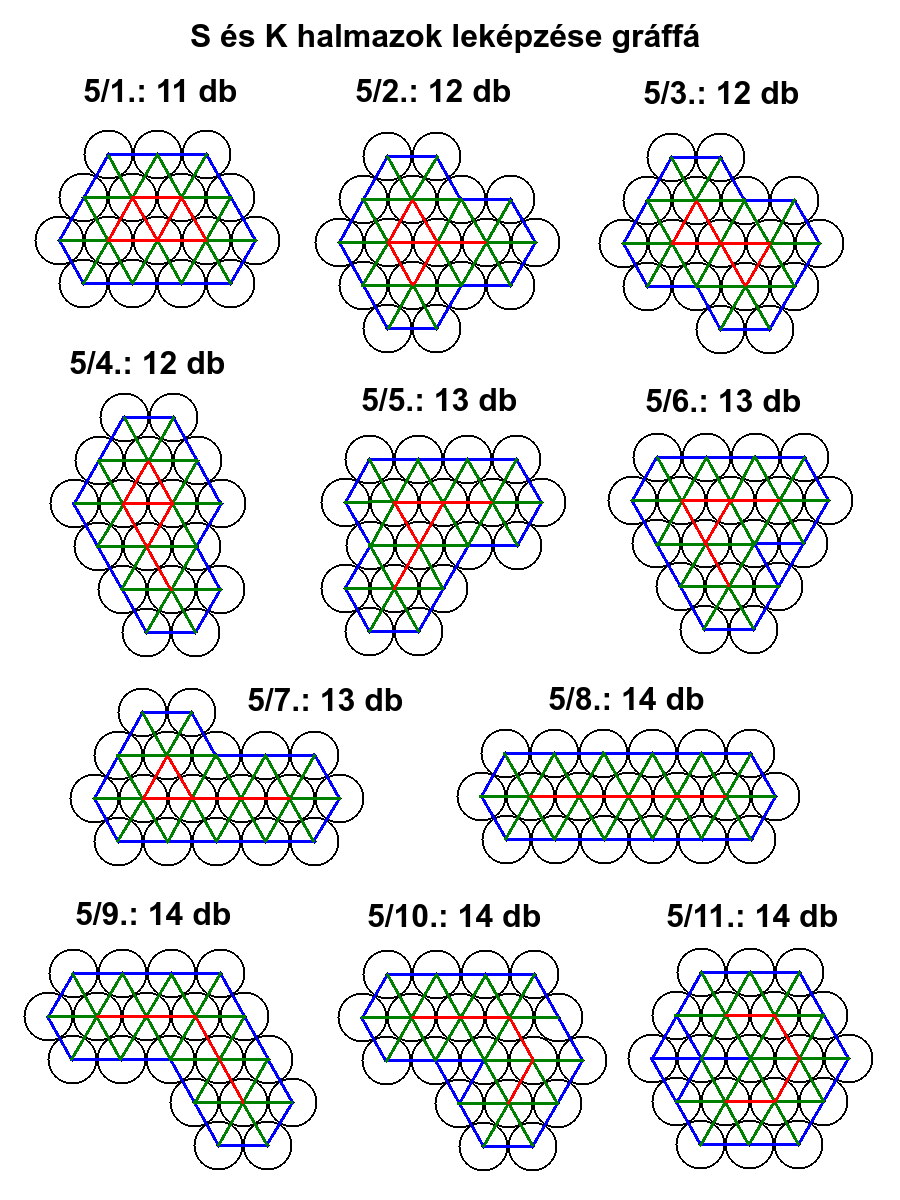
5/1. / 6 / 2+2+1+3+1+2=11
5/2. / 10 / 1+1+1+1+1+1+1+1+2+2=12
5/3. / 10 / 1+1+1+1+2+1+1+1+1+2=12
5/4. / 8 / 1+2+1+1+1+1+3+2=12
5/5. / 10 / 3+1+1+1+2+1+1+1+1+1=13
5/6. / 6 / 3+1+3+1+3+1=12 (T=1)
5/7. / 8 / 1+1+2+1+1+4+1+2=13
5/8. / 6 / 5+1+1+5+1+1=14
5/9. / 8 / 3+3+1+1+2+2+1+1=14
5/10. / 8 / 3+2+2+1+2+1+1+1=13 (T=1)
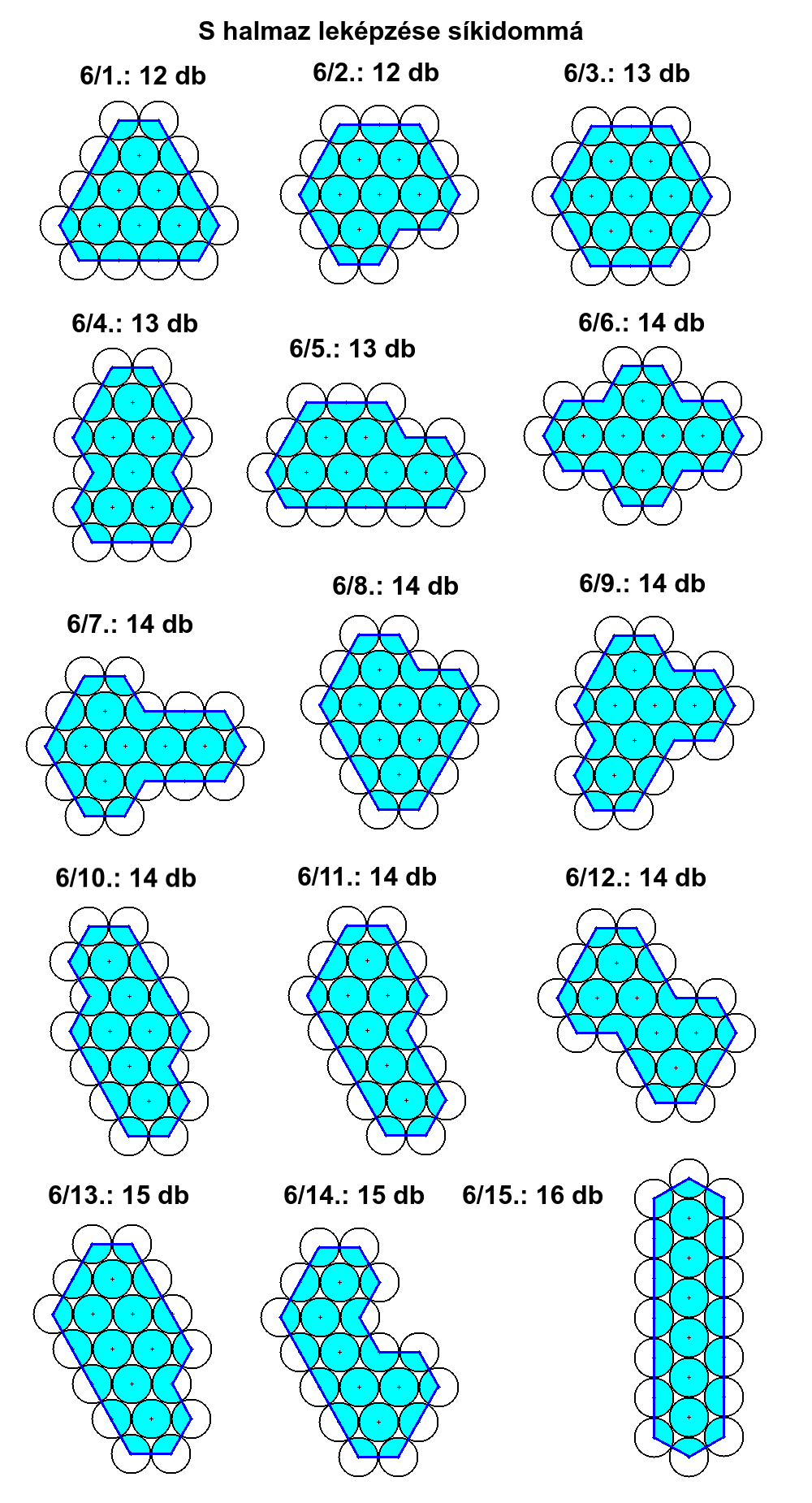
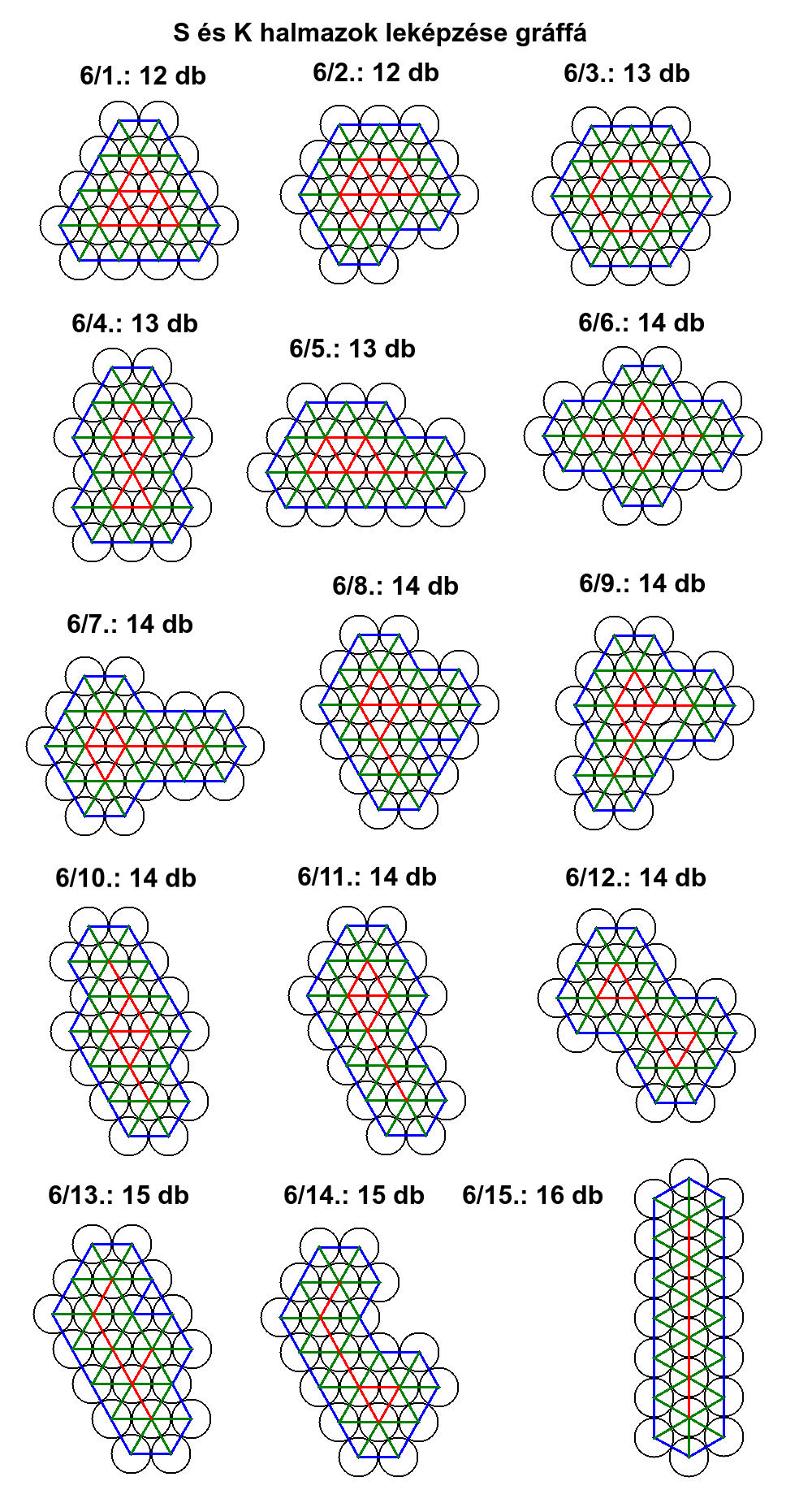
6/1. / 6 / 1+3+1+3+1+3=12
6/2. / 8 / 2+2+1+1+1+1+2+2=12
6/3. / 6 / S1: 2+2+2+2+2+2=12, S2: 1
6/4. / 10 / 1+2+1+1+1+2+1+1+1+2=13
6/5. / 8 / 2+1+1+1+1+4+1+2=13
6/6. / 14 / 1+1+1+1+1+1+1+1+1+1+1+1+1+1=14
6/7. / 10 / 1+1+2+1+1+2+1+1+2+2=14
6/8. / 8 / 1+1+1+1+3+1+3+2=13 (T=1)
6/9. / 12 / 1+1+1+1+1+1+2+1+1+1+1+2=14
6/10. / 10 / 1+3+1+1+1+1+3+1+1+1=14
6/11. / 8 / 1+2+1+2+1+1+4+2=14
6/12. / 10 / 1+2+1+1+2+1+2+1+1+2=14
6/13. / 8 / 1+3+1+1+1+1+4+2=14 (T=1)
6/14. / 10 / 1+1+1+1+1+1+2+1+4+2=15
6/15. / 6 / 6+1+1+6+1+1=16
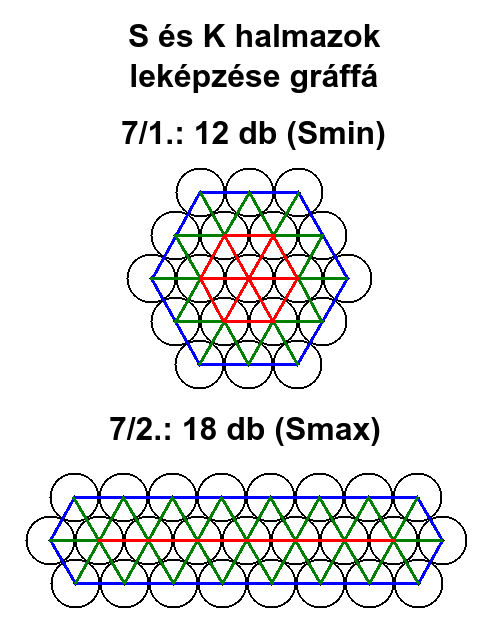
7/1. / 6 / 2+2+2+2+2+2=12
7/2. /6 / 7+1+1+7+1+1=18

5. E HALMAZ LEKÉPZÉSE GRÁFFÁ

Az E halmaz elemeinek origói megfeleltethetők egy gráf P csúcspontjainak. Az egymással érintkező körök kapcsolatai megfeleltethetők egy gráf é éleinek. Az alábbi rajzokon a K-K kapcsolatokat pirossal, a K-S kapcsolatokat zölddel, az S-S kapcsolatokat kékkel jelöltem.

Következmények:
1. Minden él egységnyi hosszúságú.
2. Az egy P csúcspontba befutó élek száma: 3<=Pé<=6.
3. A piros, zöld és kék élek egyenként összefüggő részgráfokat alkotnak.
4. A piros és kék részgráfok sehol nem érintkeznek (nincs közös P pontjuk), köztük kapcsolatot a zöld részgráfok alkotnak.
5. A piros és kék részgráfok pontjai együtt alkotják a gráf teljes ponthalmazát.

6. KITERJESZTÉSEK

A halmaz és szomszédai közti összefüggés kiterjeszthető n térdimenzióra, vagyis a 3D-s gömbök halmazának szomszédaira is felírhatók a megfelelő képletek, valamint a 4D-s hipergömbök, 5D-s extragömbök halmazaira is. Ezen kívül a modell kibővíthető egyrészt a különböző méretű n térdimenziós körök szomszédossági viszonyaira, másrészt a hézagos szomszédosságokra, amikor egy körnek nem 6, hanem csak 5 vagy 4 szomszédja lehet maximum. 3 szomszéd esetén a K halmaz körei közti hézagok már akkorák, hogy bennük pont elfér egy-egy szomszédos kör az S halmazból, 2 szomszéd esetén pedig csak nyitott végű vagy gyűrű alakú láncok képezhetők.

Mindennek számos gyakorlati jelentősége van a fizikában, kémiában, biológiában, illetve technológiai téren. Egyrészt megbecsülhető vele a halmazok felszínének beburkolásához szükséges elemek száma, a halmaz formájától függetlenül. Például adott tömegű tárgy befestéséhez minimálisan és maximálisan (egy atomnyi rétegvastagságban) mekkora tömegű festék szükséges? Másrészt az n dimenziós atomfizikában segíteni fog megbecsülni az anyagi részecskék térfogatát kitöltő fotinók várható számát, adott szaporodási ütem esetén. Valamint a részecskékben üresen maradó lyukak és öblök helye, mérete, formája is megbecsülhető lesz vele, ami a fényelnyelő képességükről ad információkat. Harmadrészt a kémiában segíthet a nagy méretű molekulák térbeli szerkezetének, konformációinak kutatásában, valamint a különböző méretű atomok rácsainak megértésében. Ugyanígy a biológiában a szaporodó baktériumok, sejtek halmazának formavilágát is le lehet vele írni, ami döntő jelentőségű a mikrobasokaság együttműködése, önvédelme, táplálkozása, mozgása, fejlődése szempontjából. A nanotechnológiában pedig a nanorobot rajokból összeállított, alakváltó tárgyak felépítése, lebontása, átformálása terén lesz hasznos mindez.

Ezen feladatok megoldása olyan bonyolult, hogy érdemes hozzá fejlett számítógépes modellező programot, illetve mesterséges intelligenciát használni. Akinek sikerült modellezni a 3D-s gömbök halmazainak lehetséges konformációit és meghatározni a szomszédossági sorozat képleteit, küldje el az eredményeket publikációként az Eseményhorizontnak és megjelentetjük.

Készült: 2024.04.19. - 05.01.

Vissza a tartalomhoz