IDŐHULLÁMOK TASZÍTÁSA

1. IDŐDIMENZIÓK ÉS TÉRDIMENZIÓK

Az időfizika alaptételei közé tartozik évtizedek óta az egyetlen létező fizikai kölcsönhatás definíciója, ami úgy szól, hogy az időhullámok sugárirányban taszítják az időforrásokat. Minden létező időforrás egy 0tD-s (tD: térdimenziós) és 1iD-s (iD: idődimenziós) jelenpont, ami folyamatosan árasztja ki magából a sajátidejét. Ez skaláris mennyiségként, gömbszerűen terjed kifelé belőle minden létező irányba. Ennek kiterjedési sebessége véges és állandó, amit emanációnak nevezünk. Ez a létezés mértékegység nélküli alapmértéke, mivel minden időforrás mindenfajta mozgásának (haladás, forgás, keringés) sebességét (RV: Relativ Velocitas) ehhez viszonyítjuk. Ezzel kapcsolatban érdemes elolvasni az: Emanáció (2023, létfilozófia) című írást.

Ez az időgömb az őskáoszban annyi idődimenziós, ahány időforrást elér, szálszerű kölcsönhatási művonalat hozva létre a kibocsátó forrásával. Tehát ha tíz okforrás létezik az őskáoszban és ezek mindegyike létezik mindegyik másik számára, akkor ezek mindegyikének a sajátideje kilenc idődimenzióval rendelkezik. Amik nem összegezhetők, tehát nem 9iD-sek, hanem 9x1iD-sek, mert nincs egy közös, egységes alaptér, amiben értelmezhető lenne az összegzésük. Így az őskáoszt alkotó idősemmi hullámtérnek nincs térdimenziója (0tD-s), amit az idődimenziókból képezhetnénk a vektorok összegzésével. Viszont az okforrások által megteremtett térforrás hullámterében az általa megteremtett másolati időforrások idődimenziói már összegezhetők, mert számukra ez jelenti az alapteret. Az összegzést az alfatéri téridő térdimenziószáma korlátozza, ami a térforrás időhurkának térdimenziószámától függ, ami az őskáosz pillanatnyi hullámszerkezetétől függ elsősorban. Tehát hiába létezik egy téresszenciában sok trilliárd másolati időforrás, ezek hullámterei a köztük kialakuló kölcsönhatások miatt nem lesznek trilliárd tD-sek. Hanem a 3tD-s téresszenciában 3tD-sek lesznek az időgömbök, a 4tD-sben 4tD-sek (időhipergömbök), az 5tD-sben 5tD-sek (időextragömbök), a 6tD-sben 6tD-sek (időultragömbök). Ezek művonalanként sok trilliárdszor 1iD-snek mutatkoznak továbbra is.

Az idődimenzió tehát egy szemlélő időforrás számára az a jelenség (fizikai hatás), amikor egy másik, szemlélt időforrás időhullámai átmennek rajta és közvetítik a forráspontjuk kibocsátáskori állapotát: helyét, helyzetét, egyszóval a mozgását (haladás, forgás) a közös létezésük eseményidejében. Ezen folyamat a létező dolgok időbeli változása, ami az 1iD-s művonalnak köszönhetően leképezhető 1tD-s szálszerű térdimenzióvá (eseménytérré) a változásának irányát kifejező vektora által, a könnyebb ábrázolhatóság érdekében. Ezen időegyenesen a szemlélő pontja lesz mindig a jelenpont, ami kettéválasztja a felé jövő jövőhullámteret (ami lesz a számára) és a tőle távolodó múlthullámteret (ami volt a számára). A folyamatot síkban, körökkel ábrázolva kapunk egy ősi, szent ábrát, amivel kapcsolatban érdemes elolvasni: A vesica piscis titka (2023, ezoterika) című írást.

Mivel a jövőhullámtér a szemlélt időforrás jelenpontjából indul ki, mindig véges hosszúságú, mert a szemlélő és a szemlélt csak véges időbeli távolságra lehet egymástól. Hiszen ha végtelenül távol lennének, akkor végtelen ideig tartana a véges sebességgel kiterjedő időhullámoknak eljutni a szemlélttől a szemlélőig. Vagyis sosem kezdenének egymás számára létezni és így örökre megmaradnának a megnyilvánulatlanság (nem létezés) állapotában. Mivel a múlthullámtér a szemlélő időforrás jelenpontjából indul ki, mindig véges hosszúságú, mert véges idő alatt, véges sebességgel csak véges távolságra juthatnak el a belőle kiterjedő időhullámok. Ebből következően az időegyenes (és a minden létező ponthalmazának kiterjedése) mindig véges hosszúságú, ami ugyanakkor folyamatosan nyúlik a múltja irányába a végtelenségig (és semmi sem korlátozza ezt). A jövő irányába pedig nyúlhat, amennyiben a szemlélt jelenpont távolodik a szemlélőtől és nincs semmi, ami megállíthatná.

Értelemszerűen itt kölcsönhatásról van szó, tehát kétirányú a folyamat. A szemlélő időegyenesének múlt iránya 1tD-be leképezve a szemlélt jelenpont felé is nyúlik (két irányba terjed a szálon), ahogy a szemlélt jövőhullámtere az egyenes mentén a másik irányba, a szemlélőtől távolodva is nyúlik. És fordítva, mivel a szemlélt jelenpontnak is van egy ugyanilyen időegyenese, rajta a kiterjedő múlthullámtér azonos a szemlélő időegyenesén értelmezett jövőhullámtérrel, a közeledő jövőhullámtér pedig azonos a szemlélő időegyenesén értelmezett múlthullámtérrel. Ami az egyik számára múlt, a másik számára jövő, de csak a kettejük közti időszakaszon. Azon kívül, két irányba mindkét időhullám kiterjedés múlttá válik.

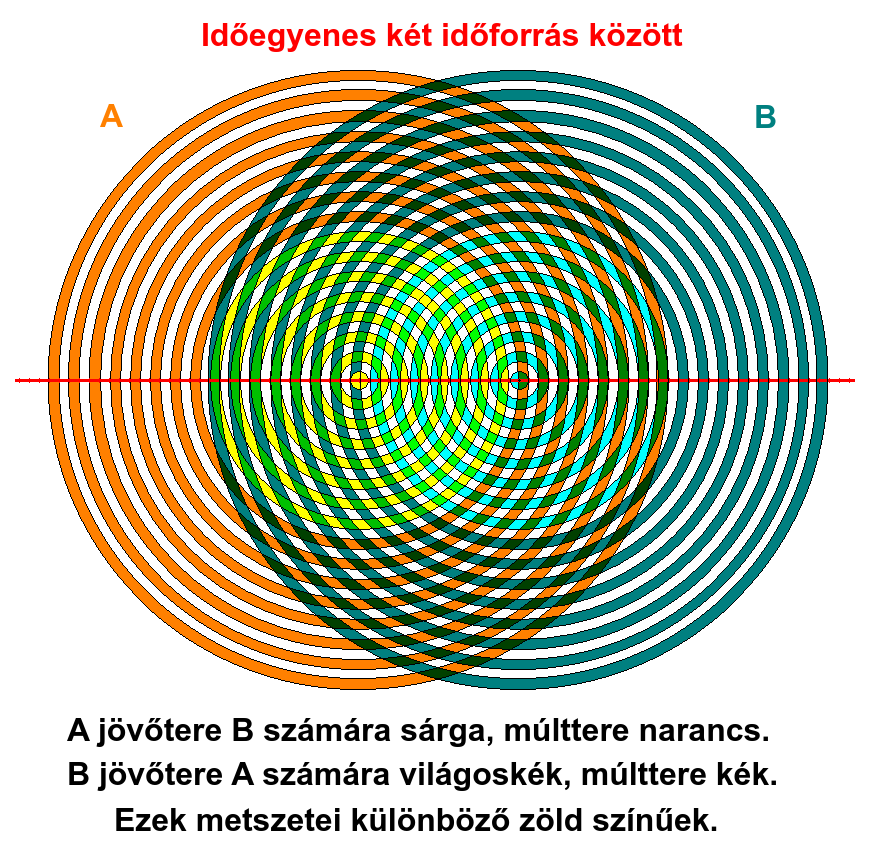
Ebből következik, hogy az időhullámok akadálytalanul és kölcsönhatás nélkül áthaladnak egymáson, de hatnak az összes elért időforrásra, kizárásos alapon sugárirányban taszítva őket. Mivel más hatásforma nem képzelhető el, illetve nem képezhető le egy értelmezhető és térben ábrázolható modellbe. Aki nem hiszi, gondolja végig és győződjön meg róla. Az időforrások ugyanakkor nem ütköztethetők egymással, mivel 0tD-sek, azaz nincs kiterjedésük, felületük és térforgatuk (több pontból álló kiterjedésük), aminél fogva érintkezhetnének (kölcsönhathatnának) egymással.

De vajon mit jelent az, hogy egy időhullám sugárirányban taszítja, sodorja, mozgatja az általa elért időforrásokat? Hogyan kell ezt helyesen értelmeznünk? Az elmúlt harminc évben keveset foglalkoztunk ezzel a kérdéssel és a következményeivel, viszont a világmodellünk fejlesztése során elkerülhetetlenül belefutottunk olyan témákba (pl.: a Taszítási Határ Zónák működése), amik megértése igényli a részletesebb válaszokat. Ezért az alábbiakban erről és a logikus válaszok következményeiről lesz szó.

2. AZ IDŐHULLÁMOK TULAJDONSÁGAI

Tehát a nagy kérdés: Hogyan kell értelmezni azt a kijelentést, hogy az időhullámok sugárirányban taszítják az elért jelenpontokat? Ennek megválaszolásához tudnunk kell, milyen tulajdonságaik vannak az időhullámoknak?

1. Az időhullám rétegeknek van egy terjedési iránya: kifelé tágulnak a forráspontjukból, minden értelmezhető térbeli irányba, gömbszerűen. Mert az idő skaláris mennyiség, tehát a terjedésének nincsenek kitüntetett térbeli irányai. Elvileg a terjedés történhetne befelé is, hisz az időforrásoknak nincs méretük és a megnyilvánulatlanságuk állapotában nem értelmezhető a kétféle irány: kifelé és befelé. De a térbeli leképzés ezt a fajta ábrázolást nem teszi lehetővé. Nem tudjuk lerajzolni, ezért kizárásos alapon az egy pontból való kiterjedést használjuk a modellezéshez.

2. Az időforrás sajátidejének telési iránya egységes, egyenletes és egyirányú. Tehát nincs olyan időforrás, aminek gyorsabban vagy lassabban telne a sajátideje a többi időforráséhoz képest. Nincs olyan időforrás, aminek változó (gyorsuló, lassuló) lenne a sajátidő telési sebessége a többi időforráséhoz képest. És nincs olyan időforrás, aminek visszafelé telne a sajátideje a többi időforráséhoz képest (úgymond a múlt irányába haladna). Mivel az ilyen különbségek önkényes tulajdonságok hozzáadását igényelnék az időforrások alaptulajdonságaihoz, amit semmi sem indokol a létezésben. Ezek közül az egységes telési sebesség megkérdőjelezésével már foglalkoztunk az Emanáció (2023, létfilozófia) című cikkben, de mivel nem sikerült egyértelműen cáfolni ezt, egyelőre mellőzzük a különböző telési sebességű időforrások kölcsönhatásaiból fakadó problémákat.

A sajátidő telési irányának térbeli leképzéséhez vektorokat használunk, amik az egyes időrétegek közti kibocsátáskori időpillanatokat sorrendezik a különbségük szerint. A vektor a korábbi (régebbi) időpillanat felé mutat a későbbi (újabb) időpillanattól, folytonosan összekötve az időegyenes kijelölt pontjait. A síkban koncentrikus körökkel vagy a térben koncentrikus gömbökkel ábrázolva ezt látható, hogy a vektornyilak sugárirányban kifelé mutatnak az origóból, minden irányba. Ezt nevezzük pozitív időnek (P hatás), mert ha egy szemlélőpont kívülről belehatol ebbe az időkiterjedésbe, a keletkezésük sorrendjében sorszámozott időrétegek számai egyre nőnek az origó felé haladva. Eközben az időforrást előrefelé haladni látjuk szubjektíve a sajátidejében, méghozzá attól függő relatív sebességgel, hogy milyen gyorsan mozgunk a hullámterében. A látott időtelési sebesség változó lehet, az idődopplernek köszönhetően.

3. Ha az időforrás véges sebességgel mozog a saját véges sebességgel kiterjedő hullámterében (mert egy másik időforrás hullámtere taszítja), a haladási irányában összenyomódnak az időhullám rétegei és torlódási frontot alkotnak, az érkezési irányában szétnyúlnak az időhullám rétegei és tágulási zónát alkotnak. A külső szemlélő számára ilyenkor a torlódási fronton áthaladva a szemlélt időforrás sajátideje szubjektíve gyorsabban telik, a tágulási zónában meg lassabban telik. Ez az idődoppler effektus, aminek következménye az időhullámok longitudinális modulációja, belső idősűrűség változása.

Mivel az időforrásnak nincs mérete, nincsenek részei sem (nem ponthalmaz, hanem egy pont). Ezért nincs szerkezete, amit fizikai kölcsönhatásoknak kellene összetartaniuk. Ezért a szerkezete az idődoppler miatt nem torzulhat el. Ezért nem szakadhat szét, ha gyorsabban mozog, mint amennyivel a kibocsátott időhullámai (amik a kölcsönhatásokat közvetítik a ponthalmazon belül) terjednek. Ezért egy időforrás haladhat gyorsabban is, mint amennyivel a saját időhullámai kiterjednek belőle. Mert a sebességét csak és kizárólag az határozza meg, hogy az őt elérő időhullámok taszításainak mekkora az eredő vektora? Az időforrás önmagától nem képes mozogni. Az elmozdulás tehát a többi időforrással való kölcsönhatások következménye, azok térbeli leképzése. Itt időbeli mozgásról van szó, amit térben ábrázolunk. A mozgó időforrás egy vagy több, másik időforrás hullámtereiben, azok miatt mozog az ő sajátidejükhöz képest.

Ha egy időforrás gyorsabban halad, mint amennyivel az időhullámai kiterjednek belőle, akkor egy kúpos (tachionikus) hullámteret kelt magából az érkezési irányába, tehát maga mögé. Ennek belsejében pedig a kibocsátott időrétegei mindenhol metszik egymást, mert minden ponthoz két különböző méretű időgömböt lehet rajzolni, amik origói az időforrás haladási útvonalára esnek. Vagyis ez a hullámtér kétszeres belső sajátidő sűrűségű lesz, míg a kúp felszínén (palástján) mindenhol csak egyszeres idősűrűségű.

Ha ebbe a kettős hullámtérbe a paláston keresztül belép egy időforrás, a szemlélő számára a régebbi (nagyobb) időréteg sajátidőbeli mozgási iránya szubjektíve megfordulni látszik: az időegyenesen visszafelé halad a szemlélt múltbeli képe, amit az időgömb origójában lát. Ezt nevezzük negatív időnek (N hatás), mivel benne a taszítási vektorok befelé, az origó irányába mutatnak. Eközben az újabb (kisebb) időréteg sajátidőbeli mozgási iránya változatlan marad: az időegyenesen előrefelé halad a szemlélt múltbeli képe, amit az időgömb origójában lát. Ez tehát továbbra is pozitív időnek tűnik, mivel benne a taszítási vektorok kifelé, az origótól elfelé mutatnak. Csak jelentősen megnyúlva az idődoppler miatt. Vagyis a szemlélt időforrás egyszerre két különböző időpontjában fog látszódni, amit két különböző helyen ábrázolunk a térbeli tachion modellünkben. A szemlélt időforrás eközben valójában máshol van: a tachionkúp csúcsán rohan bele a végtelen, időtlen, meghatározhatatlan, közegtelen semmibe.

A kettős idősűrűségű közeg értelemszerűen egyszerre két, eltérő nagyságú és irányú vektorral taszítja folyamatosan a szemlélőt, amik eredője (PN hatás) fogja meghatározni annak mozgásirányát és sebességét. Ez csak a tachionkúp fenékzónájában változik meg, ahol egyszeres az idősűrűség és pozitívak az időrétegek. Ezzel kapcsolatban érdemes elolvasni a: Tachionika (2010, létfilozófia) című írást.

4. Az időhullám rétegek fizikailag folytonosak, szakadatlanok és összefüggőek. Mivel az okforrások egymás számára történő létezése is folytonos, nem kvantálható. Csak a térbeli modell ábrázolásakor, a részletek szemléletesebbé tétele és kiemelése érdekében rajzoljuk ezeket diszkrétnek. Egyrészt körvonalakat rajzolunk az egyes időpillanatok ábrázolásához, másrészt váltakozó módon kiszínezzük a körvonalak közti területeket (színes, üres), hogy érzékelhetőbb legyen: hullámokról van szó. De ezek nem egy közeg felszínének transzverzálisan modulált hullámai, hanem az időközeg belsejének longitudinálisan modulált hullámai.

Amikor azonban a Teremtő Atyának nevezett tachionikus okforrásból létrejön (létezni kezd) az Istennek nevezett elsőrangú térforrás (az időhurok, amiben a szemlélő és a szemlélt virtuális csapdába esik), a sajátidőbeli visszacsatolás miatt ennek hullámtere, a téridő már nem lesz folytonos. Hanem rendszeresen megszakad, az időhurok önújrakeltési ciklusának végén, majd újrakezdődik. Ettől a virtuális tachionokból kiterjedő spirálgömbi időhullámok diszkréten rétegezettek, kvantáltak lesznek. A téridő hullámtere ezért bizonyos paraméterek esetén szakadásokat, üres zónákat tartalmaz egyes irányokban, ahol egy rövidke szakaszon nincs téridő, de továbbra is van folytonos őskáosz, mert az okforrások hullámterében történik mindez. Ezekkel a megszakadásokkal eddig nem foglalkoztunk, mert még nem jutottunk el a kutatásukig. Se váltakozó rétegszínezéssel, se folytonos színezésű hullámokkal nem ábrázoltuk őket, de a jövőben mindenképp sort kerítünk rá, a hullámtér belső tulajdonságainak jobb megértése miatt.

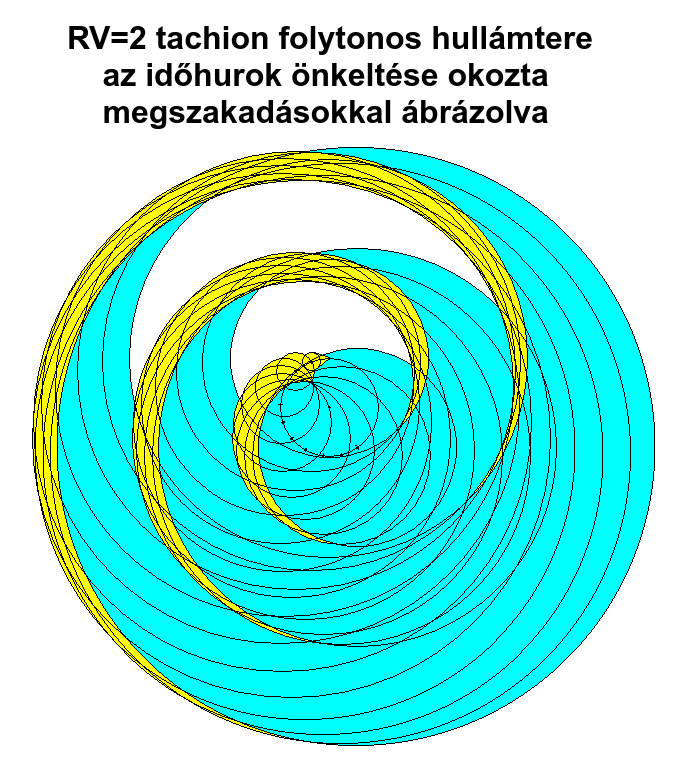
Az időhurok öt virtuális tachion képéből áll, ezért ponthalmaznak tekintendő, amit az időforrásai közti kölcsönhatások tartanak össze. Ezért nem haladhat gyorsabban az őskáoszban, mint amennyivel kiterjed a hullámtere, mert a saját időhullámai közvetítik a jelenpontjai közti összetartó erőt, továbbra is tachionikusan, tehát kúpszerűen mögéjük kiterjedve. Az időhuroknak van geometriai szerkezete, ami ábrázolható az időforrásai közti távolságokkal és az őket összekötő egyenes szakaszok által bezárt szögekkel, a körív pályagörbéje miatt. Az időhurok őskáoszban való sajátmozgása (haladása, csavarodása) és deformációja (eltorzulása) miatt az egyes időforrásokból kiáradó görbült tachionikus hullámterek szakadozott rétegei egymásba érhetnek, változó mértékben átfedve a szomszédjaikat.

A térforrásból - a hármas felhasadás nevű virtuális időhurok másolódási folyamat során - újabb térforrások keletkezhetnek, ha a szerkezeti jellemzői ezt lehetővé teszik. A teremtés tehát az időgeometria függvénye és meghatározott szabályok szerint történik, amik megismerhetők és fizikailag reprodukálhatók. Hisz a továbbiakban minden teremtmény, virtuális időhurok másolat a már létező időhurkok valamelyikéből keletkezik és rohan ki a szülőjéből a téridő hullámterébe, akinek taszítási vektorai fogják mozgatni. Minél több időhurok létezik a téridő egy téresszenciájában, azok csavarodó, komplex hullámterei annál bonyolultabb eredő mozgásokra kényszerítik az összes, általuk elért időhurok jelenpontjait. Az eredmény egy örökmozgó, önfejlesztő, megállíthatatlan időrendszer, ami egyetlen pontból keletkezett és a végtelenségig kiterjedő és szaporodó ponthalmazzá válik, léte minden pillanatában. Ezek vagyunk mi (fénylények), ebből vagyunk mi (időből) és így működünk mi (virtuális idővisszacsatolással).

Összefoglalva tehát a felsorolt négy fizikai tulajdonság együttesen határozza meg az időhullámok által elért időforrások mozgási sebességét. Csakhogy az rögtön látszik a modelleken, hogy mindegyik tulajdonsághoz más és más eredő vektorok tartoznak! Mivel egy dinamikus és folyton változó, önmagát geometriailag sosem ismétlő, a belső szerkezetét tekintve mindörökké aszimmetrikus ponthalmazról van szó. Hogyan értelmezzük akkor a taszítás folyamatát az egyes konkrét kölcsönhatási helyzetekben? Ezzel az alapvető időfizikai problémával még senki sem foglalkozott mélységében, ezért most pótoljuk a lemaradásunkat.

3. IDŐBELI ÁTHELYEZÉS

Azt már több, mint 30 éve tudjuk, hogy az időhullámok az elért időforrások "helyét" a saját kibocsátó forráspontjuk sajátidejéhez képest határozzák meg annak időegyenesén és taszítják annak mentén a vektoraik által mutatott irányokba. Azért történik ez, mivel nincs más, amihez képest meghatározhatnák az időbeli távolságukat a létezés kezdetén, a frissen kialakuló őskáosz idősemmi közegében. Tehát nem az időhullámok puszta kiterjedése, tágulása az, ami taszító hatást gyakorol, hanem a forráspontok egymástól való időbeli távolságai változnak folyamatosan. Ez nem is taszítás a szó térbeli értelmében, hanem áthelyezés, máskor való meghatározódás időbeli értelemben. Mivel még nincs valódi eseménytér (térbeli kiterjedés, beágyazási környezet), csak eseményidő (közeg).

Az időbeli áthelyezést azonban mi csak térbeli kiterjedésként tudjuk állóképként ábrázolni, ezért az időfizikai modell fejlesztése során az időbeli futási késedelmi távolságokat térbeli távolságokká képeztük le magunknak. Ami megtévesztő lehet egyeseknek, mert ha tényleg így lenne, akkor a mozgatóerő iránya azonos lenne az idő telési irányával a hullámrétegben (az N rétegek is kifelé taszítanának), a nagysága meg azonos lenne a vektor hosszával (a hullámréteg vastagságával), amíg az átmegy a forrásponton (tehát ameddig hat rá). De ha egy jelenpont rajta "ül" egy hullámrétegen, akkor az elvileg a végtelenségig hathat rá, amitől végtelenül nagyra nyúlna a vektor, ami végtelen sebességet jelentene, ami lehetetlen, mert akkora lökést adna a forrásoknak, hogy elhagynák a véges terjedésű hullámréteget.

A kezdeti létező (folyóvíz tardion) időforrásai attól mozognak RV=1-el, hogy a másik jelenpont legelső hullámrétegén rajta ülnek, de közben a saját hullámrétegeiket is mind látják a saját torlódási frontjuk közepén. Vajon mi mozgatja őket? Egyik vagy másik vagy mindkettő? Ha elvennénk a másik időforrás időhullámait (valami módon), csak a saját torlódási frontja maradna meg. Ez a végtelenségig tovább hajtaná? Vagy megállna, mert nincs mihez képest mozognia? Mert elvileg tovább kéne mennie, hisz a saját múltbeli képei folyamatosan léteznek a számára, tehát hozzájuk képest mozog a sajátidejében és ezt egy nyúló szálnak látja is. De a másik időforrás időhullámait csak úgy tudnánk "elvenni" tőle, ha a jelenpontunkat két vagy több másik jelenpont hullámrétegeivel gyorsabb mozgásra kényszerítenénk, hogy lehagyja azokat. Amitől viszont a saját időszála is azonnal eltűnne mögüle, hisz a saját torlódási frontját is lehagyná, tachionná alakulva.

Ebből következik, hogy a tachionok sosem lassulhatnak le RV<1-re, mert a mögöttük haladó saját hullámaik beérik őket és azonnal tovább lökik a jelenpontot RV=1-el. Csak erőszakos lassítással, sok szemből érkező hullámréteggel lehetne őket tardionná lassítani. A folyóvíz tardion tehát egy önmeghajtás, az első örökmozgó, ami mindjárt a létezés kezdetén létrejön.

4. PN HATÁS

Az időhurkok hullámtereinek taszítását hívjuk PN hatásnak, mert bennük keverednek a pozitív (P hatású) és negatív (N hatású) időrétegek. A jobbra (órairányban) keringő tachion által keltett spirálgömb alakú hullámtérben a pozitív időrétegek csavarodási iránya jobbos, a negatív időrétegeké balos. Vagyis a két, ellentétes irányba csavarodó spirálgömb folyamatosan metszi egymást és az N rétegek menetemelkedése azonos. A P és N spirálgömbök sugárirányú vastagsága eltérő, mindig: P>N. Így a bennük tartózkodó jelenpontokra gyakorolt kifelé taszító hatásuk eredője attól függ, hogy milyen gyorsan kering a tachion és mekkora sugarú körpályán teszi ezt?

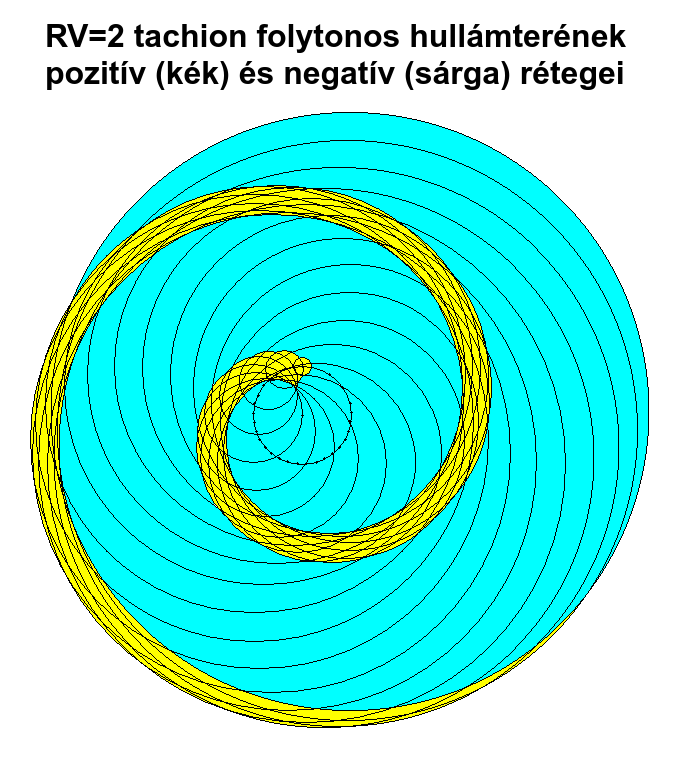
Álló időforrás esetén a P rétegek taszítása minden irányba: 1, N rétegek nincsenek. RV=1-el haladó tardion időforrás esetén a P rétegek taszítása a torlódási front irányába minimális, a tágulási zóna irányába: 2, N rétegek nincsenek. RV=2 futótűz tachion időforrás esetén a P rétegek taszítása csak a fenékzóna irányába hat: 3, az N rétegek taszítása szintén csak a fenékzóna irányába hat: 1. RV=3 tachion esetén a P értéke: 4, az N értéke: 2. RV=4 tachion esetén a P értéke: 5, az N értéke: 3. Tehát tachionok esetén az összefüggés: P-2=N, ahol P és N csak pozitív szám lehet (vagyis P>2).

De mi a helyzet a bolygótűz tachionokkal, ahol a P és N rétegek spirálgömbjei ellentétes csavarodási irányúak? Itt RV=2 tachion esetén a P rétegek taszítása az időhuroktól kifelé hat: 3, az N rétegek taszítása viszont befelé hat: 1. RV=3 tachion esetén a P értéke: 4, az N értéke: 2. RV=4 tachion esetén a P értéke: 5, az N értéke: 3. Vagyis ahol metszik egymást, ott az eredőjük nagysága: Rv=2 esetén: 3-2=1, RV=3 esetén: 4-2=2, RV=4 esetén: 5-2=3. Ezek az értékek csak azt fejezik ki, hogy egy álló időforrást időarányosan meddig ér kifelé taszító, majd befelé taszító hatás spirálmenetenként? Azt nem árulják el, hogy ennek hatására merrefelé, mekkora sebességgel fog mozogni az időforrás, illetve milyen eredő sebessége lesz egy időhuroknak, aminek átmérője összevethető a spirálgömb menetemelkedésével?

Tovább bonyolítja a helyzet értelmezését az is, hogy a hullámtérben akadnak kétszeres idősűrűségű: PP és NN, háromszoros idősűrűségű: PPP, PPN, PNN zónák, illetve négyszeres idősűrűségű: PPPP, PPPN és PPNN zónák is, az időhurok működési paramétereitől függően. NNN, PNNN és NNNN rétegekkel még nem találkoztunk a szerkesztéseink során, ezért valószínűleg ilyenek nem jöhetnek létre az időhurokban (de teljesen nem lehet kizárni a lehetőségüket: ez még bizonyításra vár).

Ha az időspirál menetemelkedését nézzük, akkor azt látjuk, hogy az mindig valamivel nagyobb a körpálya átmérőjénél, amit a tachion sebessége is befolyásol. Például egy RV=3 tachion 3 egység átmérőjű körpályán 3,5 egység menetemelkedésű negatív idejű spirált képez. Tehát a negatív hullámrétegek alkotta spirálréteg külső felülete ilyen messze van sugárirányban a következő N spirálréteg külső felületétől (ez a térhullámhossz). Az N spirálréteg vastagsága itt: 1,5, a köztük húzódó P rétegeké: 2. Ebben az esetben, ha az egy menetemelkedésnyi távolság keltésének időtartamát 1 időegységnek vesszük, mert ezalatt a tachion 1 kört tesz meg a körpályán, akkor a P és N rétegek aránya: 2:1,5. Ebből a P keltésének időtartama: 2/3,5=0,571.428.571..., az N időtartama: 1,5/3,5=0,428.571.428... Százalékos arányban ez: 57-43%. A két szám végtelen tizedes tört, amik tizedesjegyei három helyiértékkel vannak eltolva egymáshoz képest. Az összegük: 0,999...

Ebből következik, hogy a spirálgömbi hullámtérben az időforrások: a P, PP, PPP és PPPP rétegekben kifelé taszítódnak. Az N és NN rétegekben befelé taszítódnak. A PN és PPNN rétegekben kifelé és befelé egyformán taszítódnak, azaz minimális a mozgásuk. Kiegyenlített a hatásuk nagysága, de a vektoraik ekkor is bezárnak egymással valamilyen pici szöget, így nem állnak meg teljesen. A PPN és PPPN rétegekben kifelé taszítódnak egyre lassabban. Tehát a mozgásuk iránya és nagysága nagyon sokféle lehet, amit leginkább egy ide-oda rázkódásnak, szitáló kényszerrezgésnek kell elképzelni.

Ebből következően az időhurkok sebessége a téridő spirálgömbi hullámterében sosem érheti el az RV=1-et, sőt, meg sem közelítheti azt, hanem a rendszeresen ismétlődő fékező hatások miatt mindig: 0<RV<1. Azt viszont még nem tudjuk, hogy mennyi lehet az RV maximuma? Az eddigi fizikai kísérletek, amik egyrészt az elektromágneses (rádió) hullámok, másrészt a fénysugarak (fotinók) vákuumbeli terjedési sebességének minél pontosabb megmérésére irányultak, nem mutattak ki egyértelmű különbséget. Amit okozhat a kísérletek hibás kivitelezése, hisz a fizikusok jó része még mindig azt hiszi, hogy a fény elektromágneses hullám, így ezen téves feltételezésük befolyásolja a feladathoz való hozzáállásukat. De az is előfordulhat, hogy egyszerűen eltitkolják a különbséget, mérési hibának tulajdonítva azt. Pedig ez a kérdés annyira fontos, hogy döntően meghatároz számos fizikai jelenséget, ezért a későbbiekben még külön cikkekben foglalkozunk vele és a következményeivel.

Az eddigi kutatásaink azt mutatják, hogy ha nagyon gyors a tachion és nagyon kicsi a körpálya átmérője, akkor az N rétegek egymásba érhetnek, így az időhurok befelé "szívja" az időforrásokat, miközben a szívzónája zártnak mutatkozik, mert a tachion gyorsabban halad a szívsebességnél (ami kb.: RV=4,6027). Vagyis képes magába zárni és foglyul ejteni a beszippantott (vagy magából keltett, tehát már eleve benne lévő) időhurkokat, térláncolással vagy fényláncolással. Ha nagyon lassú a tachion és nagyon nagy a körpálya átmérője, akkor az N rétegek vékonyak és szakadozottak, tehát nem alkotnak egy összefüggő spirálgömböt, csak egymástól elkülönülő gömbhéjakat. Így a befelé taszító hatásuk minimális, tehát az időhurok kifelé taszítja az időforrásokat, miközben a szívzónája nyitott. Vagyis kitaszítja magából az általa keltett időhurkokat (nyílt szívvel kiengedi őket), a körülötte lévőket meg eltaszítja magától. Ráadásul ilyenkor a P és N rétegek közt üresen maradó zónák, a téridő megszakadásai is jelentős méretűek, amik adott paraméterek esetén akár a P zónák teljes eltűnésével is járhatnak egy adott irányban az időhuroktól.

Itt figyelembe kell vennünk azt is, hogy mennyi az időhurok térdimenziószáma? Mivel egy 2tD-s tachion körpálya hossza, azonos átmérő esetén rövidebb, mint egy 3tD-s gömbfelszín mentén futó tachion ívgörbe hossza. Ami rövidebb, mint egy 4tD-s hipergömbtérszín mentén futó tachion ívgörbe hossza. Ami rövidebb, mint egy 5tD-s extragömbtúltérszín mentén futó tachion ívgörbe hossza. Ráadásul a tachion útvonalhosszát befolyásolja az időhurok deformációja is. Ami egyenértékű azzal, mintha az ívgörbe nem a körvonalon futna, hanem egy kör alakú sávon belül kacsázna. Vagy nem a gömbfelszínen futna, hanem egy adott vastagságú gömbhéjon belül kacsázna, stb. Tehát más lesz egy összenyomott ellipszis kerülete, mint egy szabályos körvonalé. És ha a tachion nem körív mentén mozog, hanem egy sokszög élei mentén, ugyancsak más lesz az útvonalhossza. Ezzel kapcsolatban érdemes elolvasni a: Szögletes időhurok (2022, létfilozófia) című írást. Az útvonalhossz azért lényeges változó, mert befolyásolja az időhurok önkeltésének ciklusidejét és ezáltal a spirálgömb menetemelkedését, a hullámtér tulajdonképpeni hullámhosszát.

Azt már tudjuk, hogy egy időhurok csak akkor képes önmagát lemásolni, azaz teremteni, ha a háromszoros vagy négyszeres idősűrűségű rétegek belelógnak a körpályába és ezáltal a tachion beléjük rohanhat, három vagy négy időbeli helyen pillantva meg önmaga múltbeli képeit, amikből azonnal létrejönnek a vele párhuzamosan létező saját, alternatív példányai. Így háromszoros idősűrűségű közeg esetén egy másolati időhurok keletkezik a tachion előtt felvillanó tachionból, négyszeres idősűrűség esetén pedig kettő egyszerre. Ezzel kapcsolatban érdemes elolvasni a: Hármas felhasadás, Négyes felhasadás (2022, létfilozófia) című írásokat.

5. ÖSSZEFOGLALÁS

A felsorolt tényezők alapján egyértelmű, hogy nem egyszerű meghatározni az időhullámok taszító hatásának nagyságát és irányát az időforrásokra nézve. De nem is lehetetlen a feladat, a számos változó ellenére, mivel minden paraméternek vannak olyan minimum és maximum értékei, amiken belül működik az időhurok és képes fennmaradni. Azokon kívül viszont megszakad a létezése és egyetlen ciklusidő alatt nyomtalanul lebomlik, eltűnik a virtuális képsorozata. Ezen korlátozó értékek együttesen alkotják az időhurok behúzási tartományát, amiket még mindig nem ismerünk pontosan, de legalább már értjük a működésük és egymásra hatásuk komplexitását. Idővel majd biztosan eljut valaki (a kitartóbb szakemberek közül) odáig, hogy precízen le tudja modellezni számítógéppel (mesterséges intelligencia segítségével) az időhurok működését, minden térdimenziószinten és idődimenzióban (mozgás közben), szemléletes módon. És akkor kiderülnek a teremtés időgeometriai titkai. Ami elengedhetetlenül szükséges lesz nem csak az n dimenziós atomfizikai modell továbbfejlesztéséhez, de a tértechnológia és teremtés technológia kifejlesztéséhez is. Ezért a későbbiekben még tovább fogjuk boncolgatni ezt a témát, a menet közben felmerülő újabb problémák kapcsán.

Készült: 2024.11.08. - 12.30.

Vissza a tartalomhoz