TÖLCSÉRTÉR

1. BEVEZETÉS

Az alábbiak megértéséhez érdemes elolvasni a Szaggatér (2024, létfilozófia) és a Létfilozófia a Titán szirénjei című könyvben (2005, létfilozófia) című írásokat. Ez utóbbiban egy tölcsér alakú időgörbületről esik szó. Az itt leírtak már a téridő osztályozási rendszerbe illeszkednek, aminek kidolgozása folyamatban van, hamarosan olvashatjátok.

Egy nD-s alfatéri szerinó nem csak arra képes fizikailag, hogy nD-ben és n+1D-ben csavarodjon, hanem arra is, hogy nD-ben és n+1D-ben egyenes vonalú mozgást végezzen, valamilyen irányba, valamilyen sebességgel haladva az őskáoszban. Ilyenkor a haladási irányának vektora kifelé mutat a saját nD-s hullámterének kiterjedési irányain túlra, az idősemmibe. Mivel az alfatéri térforrás nincs benne a saját téridő hullámterében, csak kelti azt maga köré, a mozgását nem korlátozzák a saját hullámterének kiterjedési irányai. Tehát az, hogy a saját hullámterében lévő számtalan időhurok hullámterei átmennek az adott téresszenciát keltő tachion időforrásán és a vektoraik taszítják azt egy valamilyen, eredő irányba, nem jelent a szerinó időhurok egésze számára korlátozást és nem akadályozza az ezen kívüli irányokba való mozgását. Az alábbiakban azt mutatom be, ennek milyen következményei vannak a téridő hullámterének szerkezetére nézve.

2. LAPOS GÖMB ÉS HIPERKÚP

A 3tD-s (tD: térdimenzió) téridőben hat, egymásra merőleges vagy egymással ellentétes irányú vektort tudunk elindítani egy pontból: fel, le, előre, hátra, balra, jobbra. Ha ezt kibővítjük 4tD-s túltéridővé, akkor két további irányvektor adódik hozzá, amik neve: kata és hana (magyarul: Ká-Atya és Há-Anya). Az 5tD-s kültéridő és a 6tD-s feltéridő két-két további irányvektora még nem kapott neveket, mert eddig nem volt rá szükségünk. A 3tD-s kiterjedésű időhurkok csavarodása és haladása csak 3tD-ben és 4tD-ben értelmezett, mivel az ennél nagyobb térdimenziószámú irányokban történő mozgásuk nem befolyásolja érdemben a körülöttük kialakuló téridő geometriáját. Ezzel kapcsolatban érdemes elolvasni: Forgás n dimenzióban (2007, matematika) című írást.

Ha egy 3tD-s alfatéri térforrás olyan irányba mozog az őskáoszban, hogy a pályavonala (vektora) belül marad a 3tD-s hullámtere kiterjedési irányain, akkor az általa keltett téridő hullámtér gömb alakú lesz. Az emanáció sebességét nem lépheti át az időhurok spagettizálódása (szétszakadása) miatt, viszont nagyon megközelítheti. Így az idődoppler miatt a téridő gömb belülről (3tD-ből) és kívülről (4tD-ből) nézve egyaránt tardionikus marad. Viszont a 4tD (mint beágyazási környezet) irányából nézve "laposnak" tűnik, mert nincs kiterjedése kata és hana irányokba, ahonnan ránézünk. Ennek neve a továbbiakban: korongtér.

Megjegyzés: Lehet, hogy innen erednek azok a téveszmék évezredek óta, miszerint a Föld egy lapos korong az űrben. Csak azt felejtették el hozzátenni az "okosok", hogy a téren kívülről nézve. Belülről gömb alakú.

Ha egy 3tD-s alfatéri térforrás olyan irányba mozog az őskáoszban, hogy a pályavonala (vektora) kifelé mutat a 3tD-s hullámtere kiterjedési irányaiból (amik nem változnak), akkor gyakorlatilag kata vagy hana irányba mozog. Ekkor az általa keltett téridő hullámtér belülről (3tD-ből) nézve gömb, kívülről (4tD-ből) nézve viszont hiperkúp alakú lesz. Ez egy olyan 4tD-s kúp, aminek alkotója (palástja) egy 3tD-s térszín és nincs alja (alsó gömblapja; térszíne). A belsejében (túltérfogatában) tehát őskáosz van. Az emanáció sebességét ekkor sem lépheti át az időhurok, csak nagyon megközelítheti. Viszont ekkor az idődoppler miatt a téridő gömb belülről (3tD-ből) nézve ugyan tardionikus marad, kívülről (4tD-ből) nézve viszont a téridő hiperkúp tachionikusnak tűnik, noha fizikailag nem az. Mert van kiterjedése kata és hana irányokba, ahonnan ránézünk. Ez egy különös ellentmondás, amit már évekkel ezelőtt felfedezhettünk volna, csak eddig senkinek nem jutott eszébe ezt a lehetőséget is végiggondolni.

Ez a hiperkúp tehát úgy néz ki, mint egy alul nyitott tölcsér, ami a csúcsa felé mozogva növekszik és közben egyre tágul: emanációs sebességgel a haladási irányára merőlegesen vagy azzal valamilyen szöget bezárva. A neve ezért a továbbiakban: tölcsértér. A hiperkúp ugyanúgy lehet egyenes vagy ferde, mint a 3tD-s kúpok, attól függően, hogy a tengelye merőleges az alapjára vagy hegyesszöget zár be vele, de ezzel most nem foglalkozunk. A lényeg, hogy a kvintesszencia alkotja a palástját, tehát ugyanúgy benne vannak a párhuzamos téresszenciák és a nemtér-nemidő zóna, mint a korongtér spirálgömbje esetében, csak furán elnyújtva.

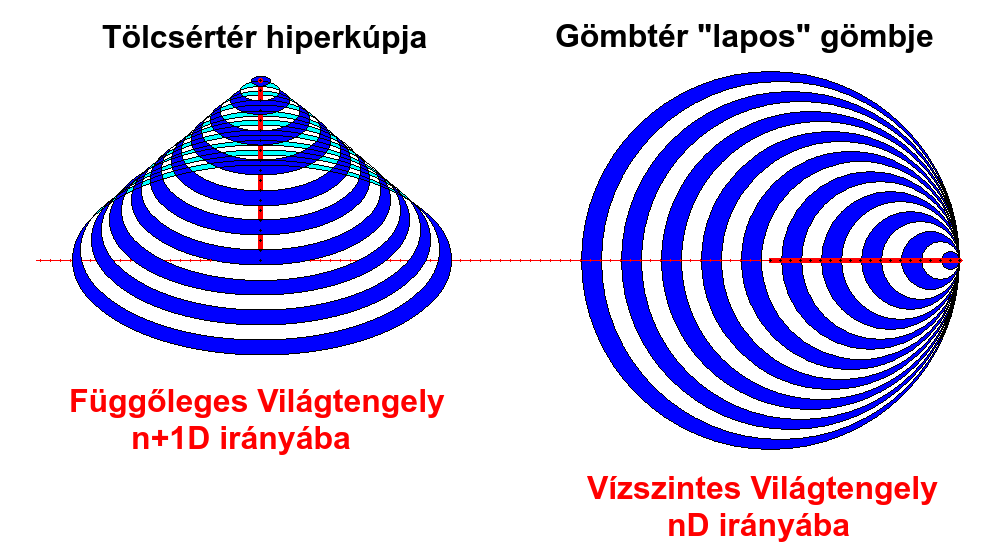
Az ilyen tölcsérterek a nemjárterek közé tartoznak, mivel a teremtmények (bétatéri szerinók, fotinók, anyagi részecskék) nem képesek megmaradni bennük, hisz a 3tD-s kiterjedésük a 4tD irányába tolódik el folyamatosan, amit nem lehet követni. De most vizsgáljuk meg tisztán elméleti alapon, mi történne, ha képesek lennénk megmaradni valahogy egy ilyen tölcsértérben? Például azért, mert a térforrásának haladási sebessége a 4tD irányába nagyon alacsony és űrhajóval követhető. Akkor nagyon érdekes eredményekre juthatnánk, lásd: az alábbi gondolatkísérleteket.

3. TÉRUGRÁSOK

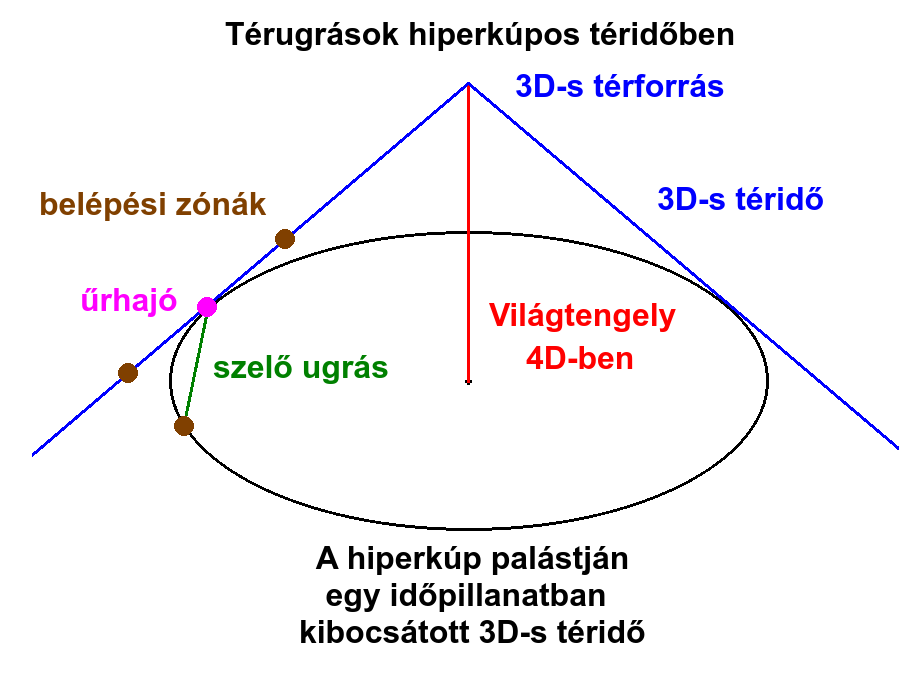
A tölcsértérben másképp is lehetne térugrásos űrhajózást végezni, mint a korongtér gömbjében. Hiszen ha tudjuk, hogy a hiperkúp palástja merre görbül: kata vagy hana irányba, illetve tudjuk, hogy tőlünk milyen irányban található a tölcsértér csúcspontja (a térforrás), akkor ennek alapján tervezhetnénk olyan, két térbeli ponton átmenő szelő egyenest, ami a hiperkúp belsejében lévő őskáoszon menne át. Ezen szakasz a térforrás irányára merőleges irányokban rövidebb lenne a térugrás szempontjából, mintha a palást mentén ugrottunk volna a térforráshoz képest sugárirányban (felé vagy tőle távolodva). Egy korongtér gömbje mentén ilyesmi nem lehetséges, mert ott bármely irányba ugorva ugyanakkora távolságokat kell megtennünk az őskáoszban, a gömb kiterjedésével párhuzamosan haladva.

A térugrás relatív rövidülése attól függene, hol vagyunk a palástban, azaz milyen messze vagyunk a csúcsától, illetve milyen irányba akarunk ugrani? Az ilyen szelő ugrásokat értelemszerűen másképp kellene végezni (és technikailag kivitelezni), mint a korongtér térszíne mentén történő párhuzamos (trapéz pályájú) ugrásokat, hisz nem lenne szükség irányváltásokra az őskáoszban. Megjegyzés: A térugrások pályáival kapcsolatos kutatási anyagok ezen cikk lezárásakor még nem kerültek publikálásra.

A hiperkúp csúcsához közeledve szűkülne a tölcsér, tehát nőne a hiperkúp egységnyi, belső (térbeli) távolságához tartozó külső (őskáoszbeli) görbülete a térforrás sugárirányára merőleges irányokban, s így az őskáoszba húzott szelő (ugrási vektor) hossza is jobban csökkenne a palást körvonalához képest. A szelő hossza maximum a palást körvonalának átmérőjével lenne azonos. Ez esetben egy ugrással átmehetnénk a palást túloldalára, vagyis ami a tölcsértérben Pi/2=1,57 egységnyi távolságra lenne tőlünk, az a szelő mentén mozogva csak 1 egységnyire lenne. A szelő ekkor átmenne a hiperkúp tengelyén is (a Világtengelyen).

Ha a térforrás irányába vagy attól távolodva ugranánk, akkor az ugrási vektor párhuzamos lenne a palásttal, tehát nem lépne fel rövidülés. Ha az ugrást nem a hiperkúp belseje felé hajtanánk végre, hanem kifelé, a külső őskáoszba, akkor meg nagyon eltávolodhatnánk a palásttól az érintő egyenes mentén, amit figyelembe kellene venni a visszatéréskor (háromszög pályájú ugrást kellene végezni).

Ez egyben azt is jelentené, hogy nagy távolságú térugrásokat végezve különböző térbeli irányokba és megmérve a hiperkúp görbületét, eldönthetnénk, hogy a mi univerzumunk "lapos" gömb vagy hiperkúp alakú? Ha nem tapasztalnánk egyik irányba sem szelő rövidülést, akkor egy korongtéri spirálgömbben élünk. Vagy olyan messze élünk a térforrástól, hogy a rövidülés mérhetetlenül kicsiny a műszereink számára (a technikai pontosság alatt van). Így akár azt is kiszámolhatnánk a szelők rövidülése alapján, milyen messze vagyunk a térforrástól? Ha ez korrelálna a más információ forrásokból származó adatok alapján végzett korábbi számításokkal, lásd: Medusa feje (2024, létfilozófia), akkor ez egy komoly megerősítése lehetne annak, hogy ezek a leírások (hindu mitológia) helyesek, pontosak. Tehát érdemes lenne a további kijelentéseiket is részletesebb vizsgálat alá venni.

4. PÁRHUZAMOS KVINTESSZENCIÁK

Mivel a tölcsérterek hiperkúpjai belül üresek, azaz őskáosz van a túltérfogatukban, aljuk meg nincs, tehát lefelé nyitottak, semmi akadálya annak, hogy többet egymásba ágyazzunk. Ehhez csak annyi kell, hogy az egyes kvintesszenciák alfatéri szerinói egy közös Világtengely mentén haladjanak egy irányba az őskáoszban, egymástól valamilyen "biztonságos" távolságra, azonos sebességgel. Így a hiperkúpjaik palástjai párhuzamosak lesznek egymással, a tölcsértereik gyakorlatilag egymásban "lebegnek", oldalirányba kiterjedve. Ezen a módon akár sok ezer vagy sok milliárd 3tD-s kvintesszencia univerzumot (nemjárteret) is elhelyezhetünk egy 4tD-s kiterjedésben (külső beágyazási környezetben) anélkül, hogy ezek valaha is metszenék egymást. A másféle szerkezetű szórványterek, nemjárterek és villámterek (régi nevükön: a térszennyezések) persze metszeni fogják őket, de mivel a nemjárterek (pl.: szaggaterek) üresek, nem fognak összeütközni semmivel a rajtuk áthaladó szórványtéri vagy villámtéri objektumok a térmetszéseknél.

Egy másik lehetőség, ha egy tölcsértér belsejébe korongtereket telepítünk, amik térforrásai a palást irányába mozognak (a Világtengelyre merőlegesen) és a kiterjedéseik párhuzamosak egymással. Mintha szintekre, emeletekre osztanánk a hiperkúp belsejét. Ekkor a "lapos" gömbök ugyanúgy nem fogják metszeni a hiperkúp palástját, mivel egyforma sebességgel tágulnak kifelé az időhullámaik. Viszont ehhez nagyon pontosan kell irányozni és mozgatni a térforrásokat, hogy a korongterek mindvégig párhuzamosak maradjanak egymással, ami egy külön technikai kihívás az istenek számára. Ezek közt viszont át lehet járkálni az őskáoszban, illetve metszhetik őket a szórványterek, másféle nemjárterek (szaggaterek), villámterek. Ezért valószínűleg ezt a módszert nem alkalmazzák a felmerülő problémák miatt.

5. TÉRDIMENZIÓSZINTEK

Az eddigiekből következik, hogy ugyanezen lehetőségeket meg lehet valósítani a felsőbb térdimenziószinteken is. Tehát a 4tD-s túltér is lehet "lapos" hipergömb alakú korongtér vagy 5tD-s extrakúp alakú tölcsértér, illetve az 5tD-s kültér is lehet "lapos" extragömb alakú korongtér vagy 6tD-s ultrakúp alakú tölcsértér az őskáoszban. Az viszont nem lehetséges, hogy a 6tD-s feltér ne csak "lapos" ultragömb alakú korongtér legyen, hanem 7tD-s kúp alakú tölcsértér is (erre még szavunk sincs), mivel a térforrások térdimenziószáma maximum csak 5tD-s lehet, a hullámterük maximum csak 6tD-s lehet, így a 7tD irányába történő mozgásukat nem értelmezzük.

Az viszont lehetséges, hogy a 3tD-s tölcsérterek egymást követő hiperkúpjai benne legyenek a 4tD-s tölcsérterek egymást követő extrakúpjainak tölcséreiben (köztük vagy mögöttük az őskáoszban), azok meg az 5tD-s téridők egymást követő ultrakúpjainak tölcséreiben. Ami elméletben szép konstrukció, a gyakorlatban viszont nincs semmi értelme és haszna.

Az eddigiekből következik, hogy a csillagtereknek (mi is egy ilyenben élünk) "lapos" gömb alakúnak kell lenniük. Mert csak ezekben képesek életben maradni a különféle teremtmények. És az egyes kvintesszenciáknak egymás nemtér-nemidő zónáiba kell beágyazva létezniük. Mert másként nem lehet őket kvázi örökre elszeparálni egymástól, továbbá a térdimenziószinteket sem lehet elzárni egymástól, hogy az istenek megakadályozzák a teremtmények ellenőrizhetetlen átmászkálását köztük. Csak így biztosítható, hogy a 3tD-s alvilágba került lelkek soha ne szökhessenek meg innen (térugrásokkal), felfelé a 4tD-s halandók birodalmába vagy az 5tD-s halhatlanok birodalmába. Lásd: Térdimenziószintek szeparációja (2023, létfilozófia). Viszont az őskáoszban létrejöhetnek olyan, a csillagtereket működtető istenektől független térszennyezések (szórványterek, nemjárterek és villámterek), amik metszik a korongtér alakú csillagtereket. Ennek következményeivel a térmetszések vizsgálatánál foglalkozunk majd.

6. TÉRNYÚLÁS

A fentiekből az is következik, hogy a tölcsérterek téridejének hullámhossza megnyúlik a korongterekéhez képest, amennyiben a térforrás sebessége azonos. Ez az egyszerűség kedvéért legyen E=1, noha fizikailag a szerinó RV<E. Így könnyebben tudunk számolni vele. Vajon mennyi lehet a térnyúlás nagysága ideális esetben?

Ha egy 1tD-s kiterjedésű korongtér Világtengelyét egységnyi hosszúnak vesszük, akkor ennek kiterjedése: 2 egységnyi (mert a kiindulási pontból az ellenkező irányba is kiterjed). Ha ezt a 2tD-ben tölcsértérré nyújtjuk, ugyanolyan egységnyi hosszú Világtengellyel, akkor a kiterjedése 2xgyök2 lesz: 2,828.427. Vagyis a nyúlás: gyök2-szeres.

Ha egy 2tD-s kiterjedésű korongtér Világtengelye: 1, akkor a körlap sík területe: 1^2xPi=Pi. Ha ezt a 3tD-ben tölcsértérré nyújtjuk, ugyanakkora Világtengellyel, akkor a kúp palást területe: Pix1xgyök2=Pixgyök2. Vagyis a nyúlás: gyök2-szeres.

Ha egy 3tD-s kiterjedésű korongtér Világtengelye: 1, akkor a gömb térfogata: ((4xPi)/3)x1^3=4,18879. Ha ezt a 4tD-ben tölcsértérré nyújtjuk, ugyanakkora Világtengellyel, akkor a hiperkúp palást térfogata: logikusan gyök2-szeres kell, hogy legyen, tehát: 5,923.843. Azt egyelőre nem tudjuk, mi a hiperkúp palástjának kiszámítási képlete, de a Pi biztosan szerepel benne, így a többi változó összértéke: 1,885.617 lesz.

Készült: 2024.12.10. - 31.

Vissza a tartalomhoz