VÉGTELEN TÖRTEK JELÖLÉSE SZÁMEGYENESEN

A számegyenes a valós számok számdimenziójának (halmazának) részleges térbeli leképzése 1tD-s szakasszá. A teljes számdimenziót nem lehet leképezni rá, mivel nem lehet 1tD-s egyenest készíteni, tekintettel annak végtelen hosszára. Végtelen dolgok ugyanis nem léteznek, mivel végtelen ideig tart a létrehozásuk, tehát sosem készülnek el.

A számegyenesnek nevezett számszakaszon az egyes számok helyét az elsőként, valahol, önkényesen kijelölt nulla ponthoz képest határozzuk meg. A pozitív számok távolsága a nulla ponttól egyenesen arányos a nagyságukkal (az általuk jelölt mennyiséggel). A negatív számok távolsága pedig fordítottan arányos a nagyságukkal. Ebből következően minden szám csak egy helyet foglal el a számegyenesből és egy helyet csak egy szám foglal el rajta.

Bár a számegyenest folytonosnak - azaz végtelen pontsűrűségűnek - tekintjük (elméletben), mégsem lehet rajta ténylegesen (a gyakorlatban) a véges számokhoz képest méretarányosan ábrázolni, bejelölni sem a pozitív és negatív végtelen egész számok értékeit, sem a pozitív és negatív végtelen tört számok értékeit. Mivel a végtelen egészek helye meghatározhatatlan, mind a nullához, mind bármely meghatározható, véges számhoz képest, tehát gyakorlatilag nincs rajta sehol, semmilyen szakaszon. A végtelen törtek ugyan rajta vannak a szakaszon, viszont végtelen számjegyből állnak, amiket sosem lehet kiszámolni, így sosem jelölhetjük be a számegyenesen őket. Aránytalanul elhelyezve ábrázolhatók, de akkor az már nem felel meg a számegyenes definíciójának, mert hozzájuk képest minden más, véges szám is csak aránytalanul ábrázolható. Ez tehát a számegyenes leképzése lesz, vagyis a számdimenzió leképzésének a leképzése, ami szükségképpen pontatlan és megtévesztő.

Hogyan lehet mégis ábrázolni az ábrázolhatatlan, ismeretlen nagyságú számokat a számegyenesen? A válasz: a jelölési mód egyszerű módososításával. A véges számokat rovátkákkal jelöljük a számegyenes szakaszán. A rovátkák egymástól való távolsága a felbontástól, vagyis az ábrázolni kívánt számok pontosságától (a szakasz pontjainak sűrűségétől) függ. A végtelen egész számokról és a végtelen tört számokról csak azt tudjuk, hogy egy adott véges számtól milyen irányban találhatók? Azt sosem tudjuk meg, hogy milyen messzire találhatók? Ezért ezek ábrázolására javaslom a következő jelölések bevezetését:

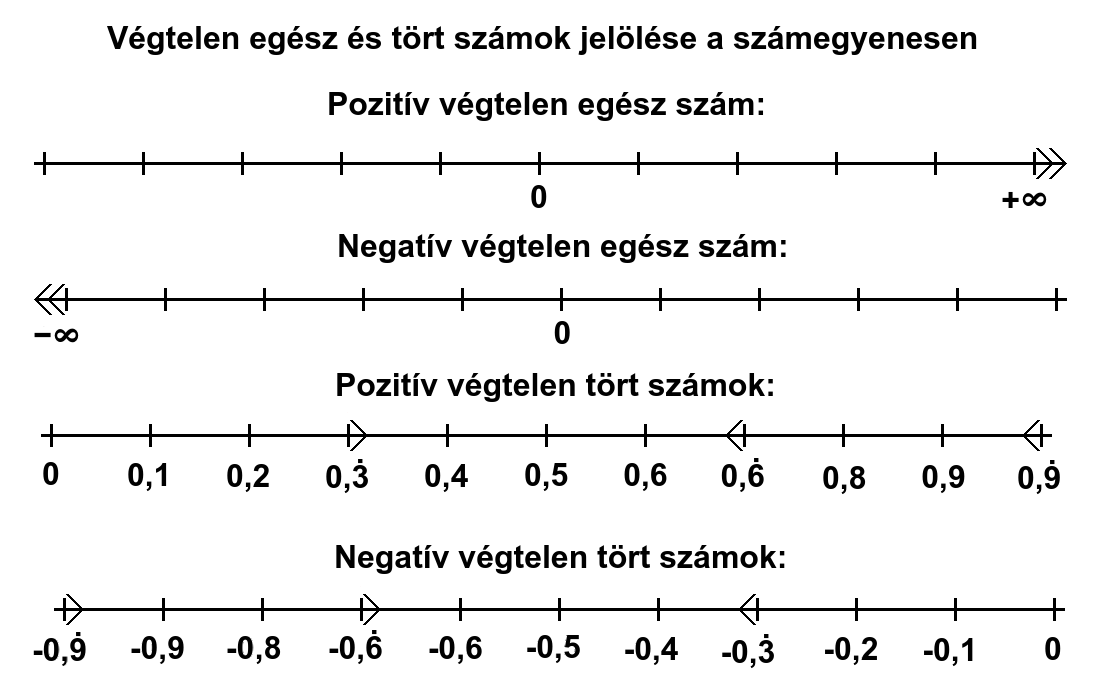
1. Pozitív végtelen egész szám jelölése:

A számegyenesből ábrázolt szakasz jobb végén kettős nyíllal. Mert az egyes nyíl csak annyit jelöl, hogy arrafelé van tovább is, tehát meghosszabbítható abban az irányban a szakasz. A kettős nyíl viszont azt jelzi, hogy arrafelé mindig van tovább is, a végtelenségig.

2. Negatív végtelen egész szám jelölése:

A számegyenesből ábrázolt szakasz bal végén kettős nyíllal. Ugyanúgy, mint a pozitív végtelen számnál.

3. Pozitív végtelen tört szám jelölése:

Ismétlődő vagy szakaszosan ismétlődő végtelen tört számok esetén a két szomszédos véges tört szám jele közül abból kell a megfelelő irányba kimutatnia egy nyílnak, amelyikhez kerekítve közelebb esik a végtelen tört (jobban közelít hozzá). Tehát a +0,333... szám a +0,1 felbontású szakaszon a +0,3 és +0,4 közt mindig a +0,3-hoz lesz közelebb, ezért valahol attól jobbra található. A +0,666... szám a +0,6 és +0,7 közt mindig a +0,7-hez lesz közelebb, ezért valahol attól balra található.

4. Negatív végtelen tört szám jelölése:

Ugyanaz, mint a pozitív végtelen tört számok esetén.

5. Transzcendens szám jelölése:

A nem ismétlődő végtelen tört számokról csak annyit tudunk, hogy a szakasz felbontásától függetlenül mindig valahol jobbra találhatók a hozzájuk legközelebbi véges számhoz, mert nagyobbak annál. Elvileg lehetne őket a felbontásuktól függően kétféleképp is ábrázolni, de ez tévedéshez vezet, valahányszor megváltoztatjuk a felbontást, ezért nem megengedett. Például a Pi értéke: +0,1 felbontás esetén: +3,1, azaz: innen jobbra nyíl a +3,2 felé. De: +0,0001 felbontás esetén már: +3,1415, azaz: innen balra nyíl lenne a +3,1414 felé. Ami nyilvánvalóan hibás ábrázolás, hisz tudjuk, hogy a Pi értéke a következő tizedesjegynél: +3,14159, azaz jobbra található a +3,1415 számtól, ezért jobbra nyíllal kell ábrázolni.

Készült: 2025.02.02.

Vissza a tartalomhoz