FIZIKA
Fizika
területei:
-Hőtan
-Elektromágnesesség
-Mechanika
-Részecskefizika
-Atom- és magfizika
-Csillagászat
-Relativitáselmélet
Mechanika:
- Dinamika
- Kinematika: A mozgások leírásával foglalkozik, de annak okával, létrejöttének feltételével már nem.
Mozgások:
-Az egyenes vonalú egyenletes mozgás
-Az egyenes vonalú egyenletesen változó mozgás
-A szabadesés
-Nem 0 kezdősebességű, egyenes vonalú egyenletesen változó mozgás
I. Mozgások leírása
A test helye, helyzete megváltozhat, azt mondjuk: a test mozog. De ez a mozgás viszonylagos, ezért szükségünk van egy olyan rendszerre, amelyben megadhatjuk a test helyét nemcsak térben, hanem időben is, hiszen minden mozgáshoz idő kell. Ezt a rendszert nevezzük vonatkoztatási rendszernek.
Legtöbbször a Földet vagy a Földhöz viszonyítva nyugvó testeket tekintjük vonatkoztatási rendszernek, mert így a legegyszerűbb megadni a test helyét, helyzetét, mozgását.
A pontos, egyértelmű meghatározáshoz viszont koordináta-rendszert használunk.

Az anyagi pontnak tekinthető test mozgása a vonatkoztatási rendszer különböző pontjaiban található, ezen pontok összessége a test pályája.
- ábra
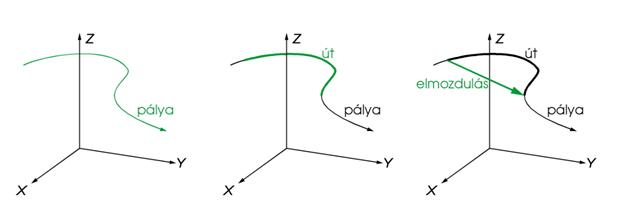
elmozdulás =
a test által megtett út, a bejárt pályagörbe hossza = s
A mozgásokat csoportosíthatjuk még a pálya alakja és időbeli lefolyás szerint is, pl.: egyenes vonalú, periodikus, egyenletes, harmonikus mozgások stb.
Egyenes vonalú egyenletes mozgás
Az olyan mozgást, amely során a test egyenlő időtartamok alatt egyenlő utakat jár be ? bármilyen kicsik vagy nagyok is ezek az időtartamok -, egyenletes mozgásnak szokás nevezni.
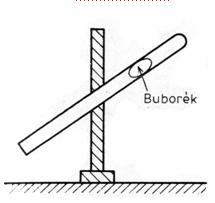
Kísérlet a Mikola-csővel
-a buborék azonos időszakok alatt azonos utakat tesz meg
-A test által megtett út
egyenesen arányos az út megtételéhez szükséges idővel, vagyis


1.: t (s) 1 2 3 4
Minden egyenletesen mozgó testnél
a
E mennyiség neve: sebesség, jele: v
kiszámítása:
v = út/ az út megtételének időtartama
v =
A sebesség SI-beli mértékegysége: m/s
A sebesség megmutatja, mekkora az egységnyi idő alatt megtett út.
A
sebességvektor
Azokat a mennyiségeket, amelyeknek nem csak nagyságuk, hanem irányuk is van, vektormennyiségeknek, röviden vektoroknak nevezzük

A test sebességvektorának nagysága a sebesség nagysága és iránya minden pillanatban megegyezik a test mozgásának irányával.
A vektorokat rajzban irányított szakasszal, ?nyíllal? ábrázoljuk. A nyíl iránya a nagyságát mutatja.
A sebességvektor jele:
A vektorok nagyságának jele:
1
Az anyagi
pont helyét, mozgását helyvektorral és annak változásával is leírhatjuk.
A helyvektor az a vektor, amely a koordináta-
rendszer origójából indul és az anyagi pont pillanatnyi helyéig tart.
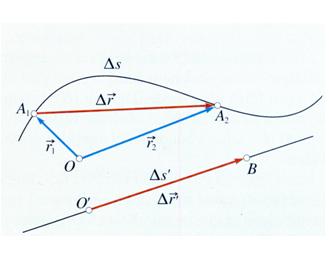
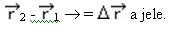
Az elmozdulásvektor hossza csak egyenes pálya esetében egyenlő az úttal.
Egyenes vonalú, egyenletes mozgások
összegzése
Egy test egy egyenes mentén, egyidejűleg végzett két elmozdulásának közös eredménye az úgynevezett eredő elmozdulás, a két elmozdulás előjeles összege:
s=s1+s2
Egy test egy egyenes mentén létrejött egyidejű mozgásainak sebessége is előjelesen adódik össze, így az eredő sebesség:
v=v1+v2
Egy test egyidejűleg végzett különféle mozgásai nem befolyásolják egymást, egymástól függetlenül játszódnak le.
Változó mozgás
Ha egy test
sebességének nagysága vagy iránya vagy mindkettő változik, változó mozgásról
beszélünk.
Átlagsebességen azt a sebességet értjük, amellyel a test egyenletesen mozogva ugyanazt az utat ugyanannyi idő alatt tenné meg, mint változó mozgással.
Átlagsebesség= összes megtett út / közben eltelt idő

Pillanatnyi sebességen azt a sebességet értjük, amellyel a test
egyenletesen mozogna tovább, ha az adott pillanatban megszűnnének a
sebességváltozást okozó erőhatások.
A pillanatnyi sebességvektor pályaérintőjének irányába esik, és arra mutat, amerre a test mozog.
Egyenes vonalú egyenletesen változó mozgás
Ha egy test pillanatnyi sebességének nagysága egyenlő időtartamonként ugyanannyival változik - bárhogy választjuk is meg ezeket az egyenlő időtartamokat -, akkor a mozgás egyenletesen változó mozgás.
Annak a testnek változik gyorsabban a sebessége, amelyiknek:
-ugyanannyi idő alatt nagyobb a sebességváltozása
-ugyanakkora sebességváltozáshoz rövidebb időre van szüksége
A sebességváltozás egyenesen arányos a közben eltelt idővel:

Ez a hányados annál nagyobb, minél gyorsabban változik a test sebessége, ezért alkalmas az egyenletesen változó mozgás gyorsulásának jellemzésére.

A szabadeséshez hasonló mozgás, csak abban különbözik, hogy a test kezdősebessége nem 0.
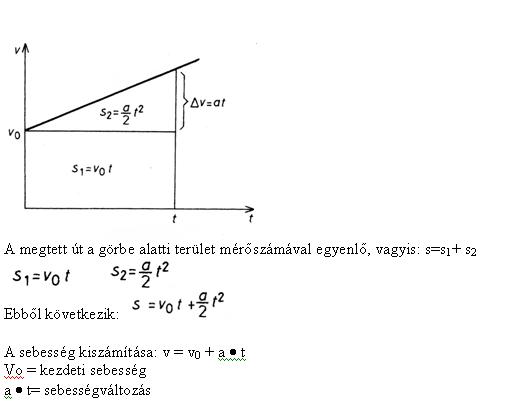
Ebből következik, ha ezt a mozgást a sebesség-idő grafikonon ábrázoljuk, egy olyan lineáris függvényt kapunk, amely nem az origóból indul ki, az egyenes mértéke pedig a gyorsulás értékével egyezik meg.


A fenti egyenleteknél mindig figyelembe kell venni, hogy mind a sebesség mind a gyorsulás vektormennyiség, így az egyenes vonalú mozgások irányának megfelelő előjeleket használjunk!
Szabadesés
A szabadesés olyan egyenes vonalú egyenletesen gyorsuló mozgás, melynél csak a gravitációs hatás érvényesül.
Ha egy test például nincs felfüggesztve, vagy alátámasztva, szabadon esik. A gyorsulás mértékét a légellenállás befolyásolja. Ugyanis a testek légüres térben egyformán esnek vagyis azonos gyorsulással.
De ez a jelenség nemcsak a Földön, hanem más égitesten is megfigyelhető.
A Földön a szabadon eső testek gyorsulását nehézségi gyorsulásnak nevezzük. Értéke függ a földrajzi helytől és a tengerfeletti magasságtól. Budapesten: g = 9, 81 m/s2, de a feladatok megoldása során gyakran csak kerekített értéket használunk: 10 m/s2.
Galilei volt az első olyan tudós, aki helyesen értelmezte a szabadesés jelenségét és ezáltal megdöntötte Arisztotelész többszáz éves elméletét, miszerint a nehezebb testek gyorsabban esnek, mint a könnyebbek. Arra a megállapításra jutott, hogy a szabadon eső testek által a t időegységek alatt megtett utak úgy aránylanak egymáshoz, mint az egymást követő páratlan számok.
Ez a kijelentés valamint az, hogy a szabadesés tulajdonképpen egy gyorsuló mozgás, egy egyszerű ejtőzsinóros kísérlettel könnyen belátható:

Végül sikerült felírnia egy általános esési törvényt, amely a Földön lévő összes test szabadesésére igaz.

A nehézségi
gyorsulás
Kísérlet
Mivel szabadesésnél nagyon rövid időtartamokat kell mérnünk, ezért mnden esetben az időmérés okoz problémát. Ebben a kísérletben egy lengő lécet, mint ingát használunk óraként.

A nehézségi gyorsulásnak viszont tudnunk kell a nagyságán kívül az irányát is, mivel vektorként kell kezelni. Ennek a vektornak az iránya lefelé mutat. Ha a szabadesés irányát vesszük pozitívnak akkor g = +9,81 m/s2
Viszont abban a koordináta-rendszerben, amelyet úgy választunk, hogy az egyik tengelye felfelé mutat:
-g = -9,81 m/s2

B.) Nem 0 kezdősebességű egyenes vonalú egyenletesen
változó mozgás
A szabadeséshez hasonló mozgás, csak abban különbözik, hogy a test kezdősebessége nem 0.
Ebből következik, ha ezt a mozgást a sebesség-idő grafikonon ábrázoljuk, egy olyan lineáris függvényt kapunk, amely nem az origóból indul ki, az egyenes mértéke pedig a gyorsulás értékével egyezik meg.
A fenti egyenleteknél mindig figyelembe kell venni, hogy mind a sebesség mind a gyorsulás vektormennyiség, így az egyenes vonalú mozgások irányának megfelelő előjeleket használjunk!
C.) Szabadesés
A szabadesés olyan egyenes vonalú egyenletesen gyorsuló mozgás, melynél csak a gravitációs hatás érvényesül.
Ha egy test például nincs felfüggesztve, vagy alátámasztva, szabadon esik. A gyorsulás mértékét a légellenállás befolyásolja. Ugyanis a testek légüres térben egyformán esnek vagyis azonos gyorsulással.
De ez a jelenség nemcsak a Földön, hanem más égitesten is megfigyelhető.
A Földön a szabadon eső testek gyorsulását nehézségi gyorsulásnak nevezzük. Értéke függ a földrajzi helytől és a tengerfeletti magasságtól. Budapesten: g = 9, 81 m/s2, de a feladatok megoldása során gyakran csak kerekített értéket használunk: 10 m/s2.
Galilei volt az első olyan tudós, aki helyesen értelmezte a szabadesés jelenségét és ezáltal megdöntötte Arisztotelész többszáz éves elméletét, miszerint a nehezebb testek gyorsabban esnek, mint a könnyebbek. Arra a megállapításra jutott, hogy a szabadon eső testek által a t időegységek alatt megtett utak úgy aránylanak egymáshoz, mint az egymást követő páratlan számok.

egyszeres, háromszoros, ötszörös stb. távolságokra apró,
nehéz tárgyakat kötöttünk. Ha az ejtőzsinórt úgy emeljük föl, hogy az alsó vége
érintkezzék a talajjal, majd elengedjük, azt tapasztaljuk, hogy a leeső tárgyak
egyenletes ritmusban kopognak, amikor a talajra esnek. Galilei ezen állítása
igaz az összes nulla kezdősebességű egyenes vonalú egyenletesen változó mozgást
végző testre. A sebesség-idő grafikonnal kapcsolatban említettek alapján Galilei
megállapítása egyszerűen ellenőrizhető.
Galileinek végül sikerült felírnia egy általános esési törvényt, amely a Földön lévő összes test szabadesésére igaz:
