Eratoszthenész és a Föld kerülete

Engedtessék meg ennek a cikknek, hogy a ma technológiai világából visszarepítse az
olvasót az ókori Görögországba, ahol még nem az államcsőddel küszködtek, hanem olyan
feladványokkal, mint a Föld méretének meghatározása.
Ugyan Hérodotosz még a korong alakú Világban hitt, más gondolkodók meggyőződése már
a gömbalak volt. Olyan bizonyítékokkal támasztották alá ezen elképzelésüket, mint az a tény,
hogy északról délre haladva, a csillagok magassága a megtett úttal arányosan növekszik –
márpedig, ha ez igaz, a mozgásnak köríven kell történnie. Ezt kiegészítendő magyarázatként
fogadták el azt is, a Föld Holdra vetett árnyéka íves, illetve hogy ha egy hegytetőn állva nem
látnak minden hegyet, egyik szigetről nem látják be az összes más szigeteket, akkor azt nem
a ködnek, hanem a Föld domborulatának köszönhetik.
Innen pedig már csak egy lépés a méretének meghatározása.
Az első nagy gondolkodó, aki ebbe belevágott a Kr.e 275-ben született Eratoszthenész
(Ἐρατοσθένης), az alexandriai könyvtár őrzője volt. Igazi polihisztor, aki jártas a
szépirodalomban, csillagászatban, matematikában.
Tőle származik egyébként az égövek geometriai meghatározása, valamint a térítők és
sarkkörök fogalma.
Eratoszthenész észrevette, hogy a Nílus-parti Szüénében (a mai Asszuán), június 23.-án
délben, mikor a Nap a legmagasabban jár az égen, éppen belesütött a nilométer (a Nílus
vízállásának leolvasására szolgáló kút) csövébe.
Pontosan egy évvel később azt vizsgálta, hogy vajon Alexandriában milyen magasan delel a
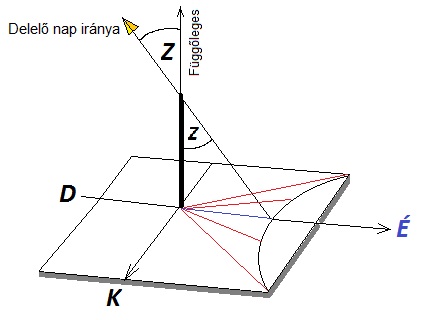
Nap. Ennek meghatározásához egy egyszerű gnómont, azaz árnyékvető pálcát
alkalmazott: figyelte, hogyan rövidül annak árnyéka: ahol a legrövidebb volt, ott delelt a Nap,
azaz akkor járt a legmagasabban. Az egymásra merőleges pálca és árnyéka meghatároz
egy háromszöget, melynek átfogója és a pálca által bezárt szög a zenitszög lesz.
Gnómon, azaz árnyékvető pálca
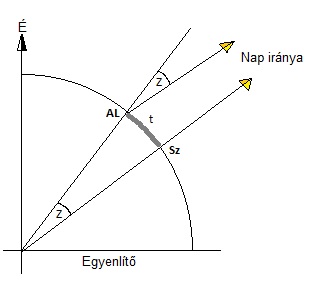
Eratoszthenész mérése alapján ez a szög 7º 12' volt: tehát Szüéne (Sz) felett a Nap a zeniten
delelt, Alexandria (AL) felett pedig, a Zenittől Z=7º 12' szög távolságban.
A Föld középpontja felé mutató alexandriai helyi függőleges és a szüénei helyi függőleges
középponti szögként szintén „Z” szöget zárnak be egymással, azaz Alexandria földrajzi
szélessége 7º 12'-cel több mint Szüénéjé. A két pont (AL és Sz) közti ívhossz (t)
ismeretében pedig aránypárral meghatározható a teljes kör kerülete, hiszen „t” úgy aránylik
a délkör kerületéhez, ahogy „Z” aránylik a 360º-hoz (a görögök is már 360º-ra osztották a
kört).
Persze, a Szüéne és Alexandria távolságának meghatározása nem kis feladat volt.
Mivel azonban Nílus-völgyében folyó öntözéses földműveléssel járó vízhasználat komoly
földmérői munkát és kataszteri térképeket igényelt, Eratoszthenész a kor színvonalának
megfelelő pontos adatokkal rendelkezett. Így a távolságot 5.000 sztadionban állapította meg.
(Egy sztadion a régi görögök mértékegység-rendszerében kb. 600 görög lábnak felelt meg.
Ma már ennek pontos hossza nem ismert méterben, ám különböző források szerint 154 és
215 méter közé esik.)
A fentiek alapján a végeredmény a Föld kerületét illetően 250.000 sztadion lett.
A mérés elve
Ez az érték elképesztően pontos és a sztadion mértékegység bizonytalan ismerete mellett is
megközelíti a ma használatos, sarkok mentén megadott, kerekített 40.000 km-es értéket.
Persze, Eratoszthenész végeredményébe a vakszerencse is közbejátszott, hiszen mérése
nagyon sok hibával terhelt.
Anélkül, hogy elvitatnánk az ókori bölcs zsenialitását, nézzünk néhány buktatót a módszerben:
---Ahhoz, hogy a (függőlegesnek elfogadott) nilométerbe június 23.-án a Nap függőlegesen
süssön be, Szüénének a Ráktérítőn kellene elhelyezkednie – ami nem így van.
---Az árnyékvető pálca, mint műszer szintén „némi” pontatlansággal terhelt.
---A két mérési helyszín közötti távolságmérés, a geodéziában mindig „gyanús” kerek 5.000
sztadionnal szintén elég bizonytalan adat.
---A legfontosabb azonban, hogy Alexandria és Szüéne nincs azonos meridiánon, Alexandria
csaknem 3º-kal nyugatra hajlik el Szüénétől.
Mindenesetre nagyszerű mérnöki teljesítmény volt Eratoszthenész Föld-kerület
meghatározása, mely érdekes módon sokáig a legpontosabb volt: az utána jövők,
Sztrabon, Ptolemaiosz pontatlanabb eredményeket produkáltak Nála.
olvasót az ókori Görögországba, ahol még nem az államcsőddel küszködtek, hanem olyan
feladványokkal, mint a Föld méretének meghatározása.
Ugyan Hérodotosz még a korong alakú Világban hitt, más gondolkodók meggyőződése már
a gömbalak volt. Olyan bizonyítékokkal támasztották alá ezen elképzelésüket, mint az a tény,
hogy északról délre haladva, a csillagok magassága a megtett úttal arányosan növekszik –
márpedig, ha ez igaz, a mozgásnak köríven kell történnie. Ezt kiegészítendő magyarázatként
fogadták el azt is, a Föld Holdra vetett árnyéka íves, illetve hogy ha egy hegytetőn állva nem
látnak minden hegyet, egyik szigetről nem látják be az összes más szigeteket, akkor azt nem
a ködnek, hanem a Föld domborulatának köszönhetik.
Innen pedig már csak egy lépés a méretének meghatározása.
Az első nagy gondolkodó, aki ebbe belevágott a Kr.e 275-ben született Eratoszthenész
(Ἐρατοσθένης), az alexandriai könyvtár őrzője volt. Igazi polihisztor, aki jártas a
szépirodalomban, csillagászatban, matematikában.
Tőle származik egyébként az égövek geometriai meghatározása, valamint a térítők és
sarkkörök fogalma.
Eratoszthenész észrevette, hogy a Nílus-parti Szüénében (a mai Asszuán), június 23.-án
délben, mikor a Nap a legmagasabban jár az égen, éppen belesütött a nilométer (a Nílus
vízállásának leolvasására szolgáló kút) csövébe.
Pontosan egy évvel később azt vizsgálta, hogy vajon Alexandriában milyen magasan delel a
Nap. Ennek meghatározásához egy egyszerű gnómont, azaz árnyékvető pálcát
alkalmazott: figyelte, hogyan rövidül annak árnyéka: ahol a legrövidebb volt, ott delelt a Nap,
azaz akkor járt a legmagasabban. Az egymásra merőleges pálca és árnyéka meghatároz
egy háromszöget, melynek átfogója és a pálca által bezárt szög a zenitszög lesz.
Gnómon, azaz árnyékvető pálca
Eratoszthenész mérése alapján ez a szög 7º 12' volt: tehát Szüéne (Sz) felett a Nap a zeniten
delelt, Alexandria (AL) felett pedig, a Zenittől Z=7º 12' szög távolságban.
A Föld középpontja felé mutató alexandriai helyi függőleges és a szüénei helyi függőleges
középponti szögként szintén „Z” szöget zárnak be egymással, azaz Alexandria földrajzi
szélessége 7º 12'-cel több mint Szüénéjé. A két pont (AL és Sz) közti ívhossz (t)
ismeretében pedig aránypárral meghatározható a teljes kör kerülete, hiszen „t” úgy aránylik
a délkör kerületéhez, ahogy „Z” aránylik a 360º-hoz (a görögök is már 360º-ra osztották a
kört).
Persze, a Szüéne és Alexandria távolságának meghatározása nem kis feladat volt.
Mivel azonban Nílus-völgyében folyó öntözéses földműveléssel járó vízhasználat komoly
földmérői munkát és kataszteri térképeket igényelt, Eratoszthenész a kor színvonalának
megfelelő pontos adatokkal rendelkezett. Így a távolságot 5.000 sztadionban állapította meg.
(Egy sztadion a régi görögök mértékegység-rendszerében kb. 600 görög lábnak felelt meg.
Ma már ennek pontos hossza nem ismert méterben, ám különböző források szerint 154 és
215 méter közé esik.)
A fentiek alapján a végeredmény a Föld kerületét illetően 250.000 sztadion lett.
A mérés elve
Ez az érték elképesztően pontos és a sztadion mértékegység bizonytalan ismerete mellett is
megközelíti a ma használatos, sarkok mentén megadott, kerekített 40.000 km-es értéket.
Persze, Eratoszthenész végeredményébe a vakszerencse is közbejátszott, hiszen mérése
nagyon sok hibával terhelt.
Anélkül, hogy elvitatnánk az ókori bölcs zsenialitását, nézzünk néhány buktatót a módszerben:
---Ahhoz, hogy a (függőlegesnek elfogadott) nilométerbe június 23.-án a Nap függőlegesen
süssön be, Szüénének a Ráktérítőn kellene elhelyezkednie – ami nem így van.
---Az árnyékvető pálca, mint műszer szintén „némi” pontatlansággal terhelt.
---A két mérési helyszín közötti távolságmérés, a geodéziában mindig „gyanús” kerek 5.000
sztadionnal szintén elég bizonytalan adat.
---A legfontosabb azonban, hogy Alexandria és Szüéne nincs azonos meridiánon, Alexandria
csaknem 3º-kal nyugatra hajlik el Szüénétől.
Mindenesetre nagyszerű mérnöki teljesítmény volt Eratoszthenész Föld-kerület
meghatározása, mely érdekes módon sokáig a legpontosabb volt: az utána jövők,
Sztrabon, Ptolemaiosz pontatlanabb eredményeket produkáltak Nála.
Vissza a GNSS cikkekhez
A polihisztor


