Egy tanítóval történő alakfelismerő eljárás adaptációja, továbbfejlesztése és vizsgálatának eredményei.
Alakzatok, jelek, objektumok, folyamatok, helyzetek felismerése és a már korábban megismertek egyikével való azonosítása az emberi agy olyan tevékenysége, amit naponta, óráról órára, percről percre, másodpercről másodprecre – néha többször is – végre kell hajtania. /1./ Ezzel a feladattal az ember idegsejtjei milliárdjainak segítségével születése pillanatától haláláig foglalkozik.
Az emberi ész ezirányú tevékenységének mesterséges úton való megvalósításával foglalkozik az alakfelismerés néven ismert diszciplina. Az alakfelismerés a gyakorlati alkalmazások terén már régen átlépte azt a határt, amikor valóban az alak, vagy valami, hasonló típusú tulajdonság felismerése volt a feladat. Hagyománytiszteletből az irodalomban általában kitartanak a szokásos elnevezés mellett.
Felületesen fogalmazva azt lehet mondani, hogy az alakfelismerő automaták a jelenségek egy jól körülhatárolt területével kapcsolatos tulajdonságok felismerésére, tehát fogalomalkotásra képesek, és ezzel olyan összefüggések megfogalmazásához jutnak el, amelyek előzetesen nem voltak ismertek. Ezt a képességüket annak köszönhetik, hogy az ember számára áttekinthetetlenül nagy adathalmazok érdemi feldolgozását is el tudják végezni.” /2./ A„fogalomalkotás” kifejezés helyett, a tények esetleges filozófiai problémákat keltő félremagyarázhatóságának elkerülése érdekében célszerűbb azt mondani, hogy ezen automaták osztályokat alakítanak ki, amelyekbe aztán besorolják a megfigyelt objektumokat. Minden osztály egy tulajdonságot, vagyis egy „fogalmat” reprezentál. Az osztályok pontos körülhatárolása egy tanulási folyamat eredménye, (innen származik az eljárás „Tanuló algoritmusok’ elnevezése), aminek két fő típusa használatos.
A tanítóval történő tanuláskor az automatának a később osztályozandó objektumok egy reprezentatív csoportját – a tananyagot – mutatják be, és a tanítás annyit jelent, hogy minden esetben megnevezik azt az osztályt is, amibe az illető objektum tartozik. Az osztályok kialakítását a a gép egy megfelelő tanuló algoritmus segítségével, ennek az információnak az alapján végzi. A másik típus, a tanító nélküli tanulásnál (cluster analízis) az osztályok kialakítása kizárólag a tananyag felhasználásával történik, valamilyen előre megadott osztályozási kritérium alapján.
Itt a gép csak olyan tananyagot (mintákat) kap, ahol a tanítás, vagyis a szóbanforgó minta minősítése nincs mellékelve, és a minták felhasználásával kell a vizsgált objektumok típusait kialakítani. Tekintettel arra, hogy ebben az esetben a felhasználható információ is lényegesen kevesebb, a lehetőségek is korlátozottabbak. Ha például eleve ismert típusokfelismerése a feladat, akkor a tanuló algoritmus által kialakított típusok és az eredetiek egyezését végső soron semmi sem garantálja. Egészen más a helyzet olyankor, amikor kiinduláskor semmit sem tudunk arról, hogy milyen típusok vannak, csak egy hatalmas és teljesen áttekinthetetlen adathalmaz adott, miindenféle értékelés nélkül. Ilyenkor a tanító nélkül tanuló algoritmus a tananyag sűrűsödési pontjainak, a clustereknek a lokalizálásával típusok megalkotását teszi lehetővé, amikről aztán részletesebb elemzéssel lehet megállapítani, hogy milyen szemléletes tulajdonságok jellemzik őket. Ez a módszer olyankor is alkalmazható, amikor a a vizsgált probléma természetéről nagyon keveset tudunk, és a vizsgálat tulajdonképpen a feldolgozandó adathalmaz elemzése első lépésének tekinthető.
A fennt vázolt elvek rendkívül széle körben alkalmazhatóak. A teljesség igénye nélkül az alakfelismerés alkalmazási területei:
- Orvosi és műszaki diagnosztika
- légi, buborék kamerás és röntgenfelvételek kiértékelése
- tapasztalati úton kapott görbék kiértékelése
- katonai alkalmazások
Végső
soron azt lehet mondani, hogy nagy adattömeg
igényes
kiértékelésére mindig
tanuló algoritmusokat célszerű
használni, mert így elkerülhetők a
tárolással
járó nehézségek.
Bármilyen tanuló algoritmus megtervezésénél az első lépés a felismeréshez alkalmazható jellemzők kiválasztása. Egy adott felismerési feladat végrehajtásakor nyilván azokat a jellemzőket kell kiválasztani és alkalmazni, amelyek az adott probléma szempontjából a legtöbb informűációt hordozzák.
Az alakfelismeerésnek ezt az előkészítő lépését lényegkiemelésnek nevezzük. Könnyen belátható, hogy a tanulás eredményessége szempontjából a lényegkiemelés az alakfelismerő folyamat legfontosabb mozzanata.
Az alakfelismerés végrehajtása különféle módszerekkel történhet. Ezen módszerek osztályozása irodalmi forrásonként változó /1/ /3/ /4/. A cluster analízis az /5/ irodalomnál például mint a komplex többváltozós elemzési módszerek egyikeként van megemlítve.
Az egyik /3/ osztályozás a következő alakfelismerő módszereket tartalmazz
1. Geometriai módszerek 1.1. Lineáris módszerek
1,2, Nem lineáris módszerek
2. Statisztikus döntési módszerek (Bayes módszer)
2,1, Normál eloszlások módszere
2,2, Szabad eloszlások módszere
3. Diszkrimináns függvények módszere
3,1, F-függvény módszere
3,2. Lineáris függvények módszere
3,3, Nemlineáris függvémyek módszere
3,4, Szakaszosan lineáris függyvények módszere
4. Egyéb módszerek
4.1. Korrelációs módszer
4.2. Regressziós módszer 4.3. Sztochasztikus módszer
4.4 Nyelvészeti módszer
4.5. Logikai összefüggéseken alapuló módszer
Nagy tömegű, általában mért adatokból felépített adatbázis esetén általában valamilyen statisztikus döntési módszer alkalmazása célszerű.
Jelen tanulmányban vizsgált alakfelismerő eljárás kiválasztása a következő szempontok alapján történt:
- Az eljárás matematikailag jól megalapozottnak látszott
- Bemeneti adatként egy Fourier-transzformáció, illetve egy
spektrumanalizátor által szolgáltatott jellemzők szerepeltek.
- Az adatredukció matematikai eszközökkel, a Korhunen-Loeve sorfejtés
alkalmazásával történt
- A döntésre felhasználat Bayes döntés aránylag jól ismert és egyszerű eljárás.
Meg kell jegyezni, hogy a bő irodalom ellenére /6-11/ az eljárás megvalósítása
során két jelentős pontnál:
-
az
osztályok
különbözőségét
kifejező
korrelációs mátrix
képzésénél,
-
valamint
az osztályba sorolási
döntésnél alkalmazott
tényezők
kiválasztásánál
mind az
elméleti alapok, mind a közölt
számpéldák
ezekben a pontokban mutatkozó elnagyolása
és következetlensége miatt
nehézségek
támadtak.
Egy
aránylag jó eredményt adó
algoritmus alapján
működő program megírása azonban
lényegesen túlhaladta volna egy adott
eljárás
adaptálásának feladatát.
Maga az eljárás két szakaszra bontható:
Tanulási szakasz
Felismerési szakasz
A tanulási szakasz folyamatai:
1. Adatbevitel.
Egy adott osztályt /X/i o számú xj vektor jellemez, ahol
j = 1,2,3,…0 i= 1,2,3,…Ml , és o = a bemeneti jellemzők, Ml pedig az osztályok száma
Az egyes osztályokat reprezentáló vektorok s számú mintavétel alapján adódnak és így egy-egy osztályt a következő adathalmaz reprezentál:
X1 osztály
X111, X112………X110
X121, X122………X120
.
.
.
.
X1s1, X1s2………X1s0
XM
osztály
XM11, XM12………XM10,
XM21,
XM22 …….XM20
.
.
.
XMs1, XMs2………XMs0
2.
A változók speciális
korrelációs mátrixainak
kiszámítása.
Kiszámítjuk az egyes osztályokat reprezentáló vektorok számtani
középértékeit a mintavételek adatai alapján.
2.2. Kiszámítjuk az egyes vektorok kovarancia mátrixait
2.3. Az egyes osztályok kovarancia mátrixainak összegzésével megkapjuk
a változók speciális korrelációs mátrixát.
3. A speciális korrelációs mátrix sajátértékeinek és saját-vektorainak kiszámítása.
4. „B” mátrix előállítása.
A „B” mátrix a nagyságrendben sorba rendezett V számú másodlagos ismérvek számának megfelelő sajátértékekhez tartozó saját-vektorból jön létre, nagysága pedig v x o.
5. A μ vektorok előállítása.
A μ vektorok a „B” mátrix és az egyes osztályok átlagvektorainak összeszorzása útján állnak elő.
Az adatmátrixok transzformációja a redukáló vektor térbe.
Az adatmátrixok ortonormálisV dimenziójú vektortérbe való transzformációja az adatmátrixok és a „B” mátrix összeszorzásával és az eredménymátrixok invertálásával történik.
7. Az inverz mátrixok determinánsainak előállítása.
8. A kiszámított értékek tárolása.
A Felismerési szakasz végrehajtásához szükséges számítási eredmények a következőek:
8.1. „B” mátrix (Vx O nagyságú tömb)
8.2. Determinánsok értékei (Ml db)
8.3. μ vektorok (Ml x V ) nagyságú tömb
A Felismerési Szakasz folyamatai:
1 Adatbevitel.
A Felismerési Szakasz a Tanulási Szakasztól elkülöníthető, végrehajtásánál csak a tanulási szakasz eredményeire, valamint a felismerendő osztály elsődleges ismérv vektoraira van szükség.
2. Az osztályba-besorolás döntéséhez szükséges számítások elvégzése
2.1. Az elsődleges ismérv vektorok transzformációja a másodlagos ismérvek terébe. A transzformációt az elsődleges ismérv vektorok és a „B” mátrix összeszorzása hajtja végre.
2.2. A Bayes-döntéshez szükséges részeredmények előállítása.
3. Osztálybasorolás döntésének elvégzése az egyes osztályokhoz tartozó számítási eredmények legkisebb eltérésének megkeresése útján.
Az algoritmus egyszerűsített blokkvázlata az 1.sz. ábrán látható.
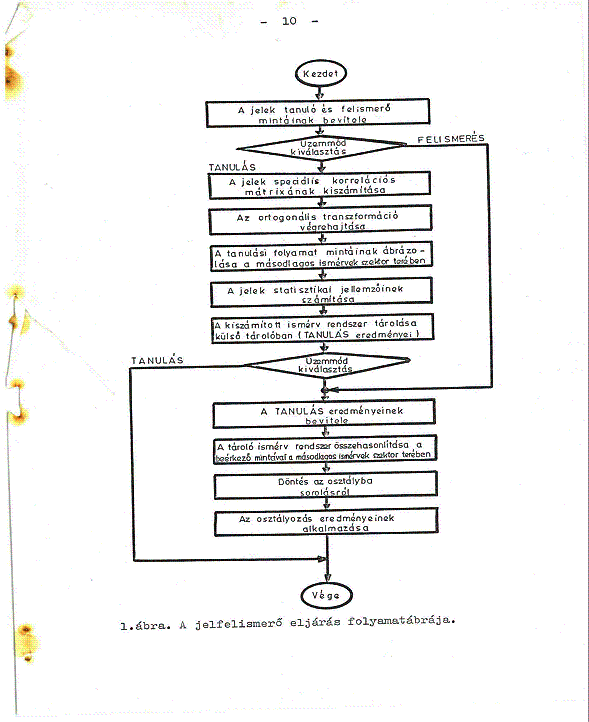
Megjegyzés: Ez az ábra a 34 évvel ezelőtt készült Tanulmány eredeti példányából származik, egyszerű digitalizálási eljárással. Látszik rajta az „idő vasfoga”, de kordokumentumként üzenetet hordoz: ezért került ebben a formában a honlapra.
Az eljárás megvalósítása személyi számítógép alkalmazásával és az eddigi tapasztalatok.
Az eljárás kezdetben egy CBM 3032 (PET) típusú személyi számítógéppel valósult meg. A BASIC nyelvű programok legutóbbi változatai egy Commodore 64 (C-64) típusú számítógépen futnak. A közölt futásidő adatok nagyjából azonosak a két típusnál. A memóriahely szükségletről közölt adatok a C-64 típusra vonatkoznak.
Az algoritmust alapjában véve két program realizálja, a Tanulási Szakaszt a TANULÁS, a Felismerési Szakaszt a FELISMERÉS program. Ezen rogramok változatai a TAN + dátum, ill. a FEL+dátum nevűek. Az egyes változatok közötti különbség alapvetően a különböző adat be- és kiviteli lehetőségek változásán alapszik.
Az – 1984 ÁPRILIS alévvel rendelkező változatoknál az adatbevitel történhet billentyűről, floppyról, és magnetofonról, valamint a CF-300 típusú spektrumanalizátorról.
A FELISMERÉS programnál a helyes döntés ellenőrzését egy beépített automatikus ellenőrző program végzi, amely azt vizsgálja, hogy a tanulási szakaszban felhasznált mintavételekre nézve milyen az ostálybasorolási döntés megbízhatósága a különböző nagyságú másodlagos ismérvek alkalmazásakor.
A program hatásossága legelőször önkényesen felvett adatcsoportokra lett vizsgálva. Az elsődleges ismérvek máma o=10 volt, a mintavételek száma 4 – 6 között változott és max. 30 volt a vizsgált osztályok száma. A vizsgált 30 osztály 152 mintavételének adatai az 1.sz. melléketben megtalálhatóak. A mellékleteket itt nem közlöm. Felkérés esetén ez ek megtekintése lehetséges.
A felvett mintaadatokra kapott eredmények:
Az 1…10 adatcsoportoknál:
|
Másodlagos ismérv szám |
Tanulási idő (perc) |
Felismerési idő (mp) |
Döntési megbízhatóság % |
||
|
Automatánál nál |
Egyedi döntésnél |
||||
|
2 |
16 |
3,6 |
6 |
98 |
|
|
3 |
15 |
5,6 |
8 |
100 |
|
Az 1…30 adatcsoportoknál
|
Másodlagos ismérv szám |
Tanulási idő (perc) |
Felismerési idő (mp) |
Döntési megbízhatóság % |
||
|
Automatánál nál |
Egyedi döntésnél |
||||
|
2 |
20 |
9,2 |
32-37 |
98 |
|
|
3 |
21 |
14,7 |
39-41 |
100 |
|
|
4 |
23 |
21,6 |
46-49 |
100 |
|
A felvett számcsoportoknál 10 db elsődleges ismérvnél az első 10 számcsoportnál (osztálynál) 100%-os felismerést kaptunk, amennyiben a másodlagos ismérvek száma V=3 volt, míg a 30 osztálynál ez a felismerési megbízhatóság V=4-nél jelentkezett. A részletes vizsgálati eredmények a 2-6. mellékletek alapján tanulmányozhatóak.
Az automatikus osztálybasorolás esetén a program a tanulási szakasznál a betanításnál alkalmazott mintavételről viszgálja automatikusan, hogy az adott mintavételt a felismerési szakasz melyik osztályba sorolja. A hibásan felismeert mintavételek adatai külön kiíródnak. Lehetőség avn bármilyen minta billentyűről történő bevitelére. Eredményként a képernyőn és/vagy nyomtatásban megjelenik a beadott minta, döntés az adott minta osztálybasorolásáról és egy jelzőszám, aminek relatív értéke a besorolás erősségét mutatja.
A 2.sz. melléklet alapján a CS10 /1-CS10/10 jelzésű 10 adatcsoportnál (mintavételek száma összesen 50) amikor a másodlagos ismérvek száma 2 volt, egy, a CS10/9 –hez tartozó minta (4,sz, mintavétel) hibásan lett felismerve. Egyedi döntési üzemmódnál bebillentyűzve ennek a mintának értékeit a számítógépbe, a második helyen tűntette fel.
A 3.sz melléketen a másodlagos ismérvek V=3 esetén az automatikus felismerő üzemmódnál mind az 50 mintavétel osztálybasorolása az eredeti osztályoknak megfelelően történt. A V=2 esetén hibásan besorolt mintavételnél a döntés erősségére utaló jelzőszám és a helyes döntés jelzőszáma között nagyságrendi eltérések mutatkoznak. Ez a nagyságrendi eltérés mutatkozik meg a 3.melléklet 2. oldalán, ahol az eredeti tanulásnál felhasznált osztályok egyikére sem jelemző mintákkal történt besoroláshoz tartozó jelzőszámok tanulmányozhatóak. A fennti gondolatmenetnek megfelelő vizsgálatok eredményei 30 osztálynál (összesen 152 mintavétel) láthatóak a 4-6.sz. mellékleteken.
Következő lépésként valódi jelek mintáinak vizsgálatát hajtottuk végre. Kilenc adó ugyanazon számcsoportokkal ellátott lyukszalagról moduláltunk Al üzemmódban
WPM-22 sebességgel. Az egyes adók műsorának vétele egy REV-251 típusú vevőkészülékkel, míg a jelek rögzítése kb 1-1 perc időtatamig NAGRA típusú magnetofonnal történt 19 cm/sec sebességgel.
A kilenc adótól származó felvétel különböző sorrendben 3-6-ig terjedő mintaszámban összesen kétszer harminc minta formájában egy másik NAGRA magnetofon segítségével átmásoltuk.
A mintákat tartalmazó magnetofon szalagot megkapta egy kutató intézet jelfeldolgozással foglalkozó részlege feldolgozás és értékelés céljából.
A kutató intézet a kapott mintákat az általuk kifejlesztett NE-400 típusú gyors A6D konverter és az ehhez csatlakozó NE-500 típusú programozható és távvezérlő adatgyűjtő készülékkel digitalizálta. A digitalizált mintákat (Egy minta=100 mért adat) páronként összehasonlítva adatredukciót hajtottak végre, aminek eredményeként kilenc számjegyet kaptak. A kilenc számjegy páronkénti értelmezése a Következő volt /12/:
1. Első minta amplitudó hisztogramjának átlagértéke
2. Második minta amplitudó hisztogramjának átlagértéke
3. Első minta amplitudó hisztogramjának szórása
4. Második minta amplitudó hisztogramjának szórása
5. Első minta amplitudó hisztogramja regressziós egyenesének meredeksége
6. Második minta amplitudó hisztogramja regressziós egyenesének meredeksége
7. Első minta amplitudó hisztogramja regressziós egyenesének és az Y tengelynek metszéspontja.
8. Második minta amplitudó hisztogramja regressziós egyenesének és az Y tengelynek metszéspontja.
9. A két minta amplitudó hisztogramja kereszt korrelációs együtthatója.
A kapott számsorokkal kapcsolatban végzett különböző viszgálatok az általunk megadott mintákra vonatkoztatva negatív eredménnyel zárultak. Az adók azonosításának feladatát, egy tanító nélküli, vagy öntanuló felismerést nem sikerült végrehajtaniuk.
Más módszert keresve az azonos adókhoz tartozó minták amplitudó hisztogramjainak értékeit (100 érték) a rendelkezésre álló számítógép kis méretű memóriája miatt tizesével összeadva és ezen értékek számtani átlahából képezett számsorok alapján a kapott minták és ezekből származtatott tanulási osztályokon végzett viszgálatok a következő eredményt adták:
A 8.sz. melléket tartalmazza a V=2 esetén kapott eredményeket. A V=3 esetén a tanulási szakasz az E/10 adatcsoport szórása nem elégítette ki az ortogonális transzformáció azon feltételét, az osztályhoz tartozó mintavételek korrelációs mátrixának a determinánsai létezzenek. A feltétel nem teljesülését az amplitudó hisztogramok előállításánál elkövetett eljárási hibára tudom visszavezetni. Az amplitudó hisztogramok értékeit lyukszalagon, készen kaptam.
A hibásnak mutatkozó E/10 csoportot a vizsgálatból kiiktatva kapott eredmények a 9-10.sz. mellékletben láthatóak. Nyolc osztály (27 mintavétel esetén) V=2 másodlagos ismérvnél a felismerés megbízhatósága 77,8%. V=3-nál 100% megbízhatóságú felismerés mutatkozott. A felismerés erősségére a felvett adatcsoportoknál tapasztaltak is igazolódtak.
A CF-300 típusú ONOSOKI gyártmányú hordozható FFT analizátor beszerzése után a viszgálatok saját mért adatokkal folytatódtak.
Az FFT analizátor vezérlése a CBM 3032 típusú számítógép IEEE 488 buszán keresztül történt és egy 3310B típusú függvénygenerátor különböző frekvenciájú sinus, háromszög, négyszög, fűrész és impulzus alakú jelformáinak spektrális komponensei voltak a TANULÁSI szakasz bemeneti adatai.
Az analizátortól egy spektrumra jellemző 200 adatot huszasával összeadva és átlagolva, 10 elsődleges és 3 másodlagos ismérv, 20 osztály összesen 100 mintavétal (osztályonként 5-5) eredményeképpen a FELISMERÉS megbízhatósága 82 %-os volt.
Érdekes eredményt hozott az eljárás vizsgálata egy karakter felismerési feladat végrehajthatósága szempontjából.
Tanulási anyagként ötször hetes mátrix alakú számjegyek, a Q és az O betűk formáinak szabályos és rontott variációi szerepeltek. Az egyes osztályokat (karaktereket) reprezentáló adatcsoportokat 5x7-es raszterben kitöltött négyzetek oszlopösszegeinek 100-al történő szorzataként állítottam elő. Ahol ez az összeg 0 volt, vagyis az adott oszlopnál egy karakterpont sem helyezkedett el, ott az adatsorba 1- et írtam.
A vizsgálati csoportoknál az alakfelismerési eljárás megfelelő hatékonyságúnak bizonyult. Az eljárás nem szereti az olyan osztályokat jellemző adatokat, ahol nem teljesül az ortogonális transzformáció végrehajthatóságának feltétele.
A módszer olyan gyakorlati területeken alkalmazható, ahol adott annak a feltételnek teljesülése, hogy a felismerésre, azonosításra felhasznált adatok ténylegesen reprezentálják a felismerendő osztályokat.
Az eljárás egy matematikai adatredukciót hajt végre és ez a matematikai redukció (lényegkiemelés) jól kiválasztott kiindulási adatok esetén igen hatásosnak ígérkezik.
Az osztálybasorolás döntésénél alkalmazott számok mennyiségi viszonyai alapján téves döntés esetén is lehetőség van bizonyos követeztetések levonására egy helyes döntést illetően.
Ez utóbbi pont alapjában véve az eddigi kísérletek tapasztalataira alapul. A tapasztalati tényeken alapuló hipotézis matematikai vizsgálata még nem történt meg.
Tervezem a módszer további vizsgálatát üzemmódok, adók azonosítási feladatai végrehajtásának területein. Úgy érzem, az eddigi vizsgálataim és a közölt eredményeim előrevivő lépéseknek tekinthetőek az alakfelismerés és a komplex többváltozós analitikai vizsgálati módszerek alkalmazásának bevezetése érdekében.
Budapest, 1984.
(Gerlits Péter mk. alezredes)
IRODALOMJEGYZÉK
1.
A.L.
Gorelik, V.A. Szkripkin: Metodi
Raszpornavanja.
Moszkva, 1977, Vizsaja
Skola
2. Fritz József: Az alakfelismerés statisztikus módszerei
Budapest, 1974 MTA Matematikai
Kutató Intézet
3.
L.T. Kuzin: Osznóvi
Kibernetiki
Moszkva. 1979.
Energia
4. J.T.Tov, R.C. Gonzales: Pattern Prognitron Principals
Addison-Weslex
Publishing Company 1974
5. Lőrincz Sándor: Komplex, többváltozós elemzési módszerek
Alkalmazása a műszaki fejlesztő munkában
Ipargazdaság.
33. kötet
10.sz.
6.
V.A.
Omelcsenko: Osznovi
szpektrálnoj teorii roszponanánija
szignalov, Szoobsenie I.
Nesztacionernije szignali.
Rádiótechnika,
1976. 38.sz.
44.o.
7.
V.A.
Omelcsenko: Osznovi
szpektrálnoj teorii roszponanánija
szignalov, Szoobsenie II.
Sztacionernije szignali.
Rádiótechnika,
1976. 38.sz.
49.o.
8.
V.A.
Omelcsenko: Osznovi
szpektrálnoj teorii roszponanánija
szignalov, Szoobsenie III. Vremennije
i szpektrálnie priznaki.
Rádiótechnika,
1976. 39.sz.
31,o
9.
V.A.
Omelcsenko: Osznovi
szpektrálnoj teorii roszponanánija
szignalov, Szoobsenie IV.
Sztacionernije Gaussovije szignali
pri apriornoj nedosztatocsnosztyi. .
Rádiótechnika,
1977. 41.sz.
12.o.
10. V.A. Omelcsenko, V.,V. Balabanov: Raszpoznavanie
szignalov pri szpektru na báze analizátorov parallelno – poszledabatelnovo tipa.:
Rádiótechnika,
1977. 41.sz.
37.o.
11. V.A. Omelcsenko, V.,V. Balabanov, V.V. Klimenko:
Ekszperimentálnoje isszledovanie raszpozananija szignalov pri
Szpektru.
Rádiótechnika,
1977. 42.sz.
30.o.
12. O-13, Tudományos kutatási zárójelentés.
Budapest, 1982.
.