Hogyan is tárolja a számítógép az olyan egyszerű adatokat mint egy szám vagy
egy mondat kettes számrendszerben? Mik vonhatóak le ezekből? Mik azok a
bitműveletek?
I, Hány bites a géped?
II, Alaptípusok
a, Sorszámozott típusok
2,
Az előjel nélküli számok
3,
Az előjeles számok
5,
A logikai típus
8, A
karakter típus
b, Egyéb típusok
4, A
valós számok
6, A void
típus
7, A
mutató típus
9, A
szöveg típus
10, A dátum/idő típus
I, Hány bites a géped?
Ez a kérdés alapjában meghatározza a számítás módját, méghozzá a processzor aritmetikai egységének számítási képességét (lásd: A számítógép alkatrészei).
A hány bites kérdés alapvetően azt határozza meg hogy hány bináris számjeggyel tud a gép egy időben dolgozni. Az hogy ez mekkora adatokat eredményez kis kombinatorikával számítható.
Azt tudjuk hogy egy biten két lehetőség van mindig (1/0, igen/nem). Gondoljuk végig hogy mennyi különböző variáció állhat elő pl. négy biten:
Ekkor az első bináris számjegy helyére kerülhet 1/0, a második helyére is, és így tovább. Ebből következik hogy a lehetőségek száma:
N = 2 * 2 * 2 * 2
N = 2^4
N = 16
Tehát összesen 16 különféle állapot állhat elő. Nézzük meg ez egy 32 bites processzor esetén mennyi?
N = 2^32 = 4294967296
Nos, ez már elég sok, lényegében bőségesen elég - vagy mégsem?
2, Az előjel nélküli számok
Egy ilyen szám átváltása kettes számrendszerbe nem egy nagy kaland, csak elosztogatjuk kettővel és felírjuk fordított sorrendben a maradékokat. Íme egy példa:
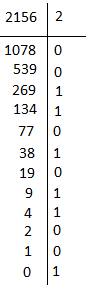
Az eredmény tehát: 1001 1010 1100, és mivel ez a szám mindössze 12 bitből áll eltárolható egy 32 bites adatként.
Az eredmény 32 biten: 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 1001 1010 1100
A számítógép az előjel nélküli számokat így tárolja egészen egyszerűen, és mivel hogy a nulla is része ennek a halmaznak a határok [0 .. 2^32 - 1] -ig terjednek.
Mivel a memóriacím (lásd: A számítógép alkatrészei) is egy ilyen szám alapvetően meghatározza hogy mennyi fizikai memória lehet a gépben. Ha megnézzük hogy mire elég 4294967296 byte, osztogassunk egy kicsit - azt kapjuk hogy ez pontosan 4 GB - vagyis e határ fölött nem tudja a gép megcímezni a memóriát 32 biten - ezért vezették be a 64 bites masinákat és rendszereket.
A C/C++ nyelvben ilyen típusú változók felvételére több lehetőségünk is van [8 bit = 1 byte]:
- 8 bit (1 byte) [0 .. 255]: unsigned short short int, vagy unsigned char
- 16 bit (2 byte) [0 .. 65535]: unsigned short int
- processzornak megfelelő: unsigned int
- 32 bit (4 byte) [0 .. 2^32 - 1]: unsigned long int
- 64 bit (8 byte) [0 .. 2^64 - 1]: unsigned long long int
Megjegyzés: Egy másik számrendszerbeli szám visszaváltása tizesbe,
helyiértékes logikával történhet:
A tizes számrendszerben, minden számjegy egy 10^x szorzót
jelöl, vagyis kettesben ez 2^x, tizenhatosban 16^x, stb.
Pl.: 0x3AC visszaváltása tizesbe [A=10, B=11, C=12, D=13, E=14, F=15]
| 3 * 16^2 = 768 | A * 16^1 = 160 | C * 16^0 = 12 |
| 3 | A | C |
Így 0x3AC = 768 + 160 + 12 = 940
3, Az előjeles számok
Az előjeles számok képzésének alapja hogy a legelső bit jelöli hogy a szám negatív-e. Ha igen akkor érvénybe lép az ún. komplementer képzés (neten rengeteg leírás van róla), a lényeg hogy a 32 db bináris 1-es a decimális -1, és a 32 db bináris 0 a decimális 0.
Mivel egy bittel kevesebb van a tartomány feleződik így a határok is változnak (felvételkor a signed/unsigned kulcsszó elhagyása esetén signed típusú lesz a változó):
- 8 bit (1 byte) [-127 .. 126]: signed short short int, vagy signed char
- 16 bit (2 byte) [-32768 .. 32767]: signed short int
- processzornak megfelelő: signed int
- 32 bit (4 byte) [2^31 .. 2^31 - 1]: signed long int
- 64 bit (8 byte) [2^63 .. 2^63 - 1]: signed long long int
4, A valós számok
A valós számok több byteon vannak tárolva mint az int típus, és bonyolultabb is működésük, a neten szintén van leírás "lebegőpontos számok" címszó alatt.
- egyszeresen pontos (single): float
- kétszeresen pontos (double): double
- többszörösen pontos (long double): long double
A valós számok sem képesek végtelen pontos értékeket tárolni, a linken további információk érhetőek el a határokról. Mivel ez az állítás fennáll, sok esetben a számítások durva pontosságvesztéssel járhatnak (pl. float esetén), ha az adott szám végtelen tizedestört.
5, A logikai típus (igaz/hamis)
Bármely olyan sorszámozott típus, ami ha nulla akkor az állítás hamis, egyébként igaz.
6, A void típus
A void típussal direkt módon nem vehetünk fel változót, de helyettesíthet más típust, jelölve hogy "nincs típusa" a változónak, vagy ha van is az érvénytelen. A függvényeknél/mutatóknál van nagy haszna.
7, A mutató típus
Említetve már a memóriacímeket többször is, érdemes bevezetni magát a mutató típust - ami egy előjel nélküli szám (lásd: A számítógép alkatrészei), de ettől függetlenül még lehet típusa.
pl.:
- int* - egy int típusú változó memóriacímét tartalmazza
- char* - egy char típusú változó memóriacímét tartalmazza
- float* - egy float típusú változó memóriacímét tartalmazza
- void* - egy változó memóriacímét tartalmazza, de nem tudni milyen típusúét (talán nem is fontos?)
Megjegyzés: Létezik egy típus nélküli érvénytelen mutató, a NULL. Ezt lehet minden olyan helyre használni, ahol mutató helyett nem akarunk átadni semmit.
Figyelmeztetés: Minden mutatóművelet veszélyekkel jár - ha az adott mutató rossz helyre mutat, vagy NULL akkor jó eséllyel össze fog omlani (védett mód szépségei).
8, A karakter típus
Néha szükséges lehet az is hogy betűket is tároljunk a gépen, hiszen a szöveges közlésnek ez az alapja. Ezt úgy érték el hogy minden egyes billentyűnek adtak egy számot (igen már megint), és ezeket kódtáblába tették. Több ilyen kódtábla van, mivel hogy a sok nyelv karakterei nem fértek bele 1-1 bájtba.
Mivel hogy az első kettő egy bájton van tárolva, míg a Unicode két bájtos erre a szövegeknél oda kell figyelni.
Természetesen ezektől eltérő kódlapok is léteznek, de ezek a leghagyományosabbak.
Megjegyzés: A programban lehetőség van az ékezetes karakterek helyes kiíratására is, ha a programot 852-es kódlappal mentjük el (a Notepad++ képes erre). Ennek hatására az IDE-ben nem lesznek jól olvashatóak az ékezetes karakterek, de a lefordított programban igen.
9, A szöveg típus
A C/C++ nyelvben a nyers szöveges típus jele a char*, illetve Unicode esetben a wchar_t*.
Ha már egy karaktert tudunk számmal leírni az korrekt, de egy egész mondat leírása azért már összetettebb. Ezt a gép úgy éri el hogy felveszi egymás utáni memóriaterületekre a karaktereket (tömb/vektor), és az első memóriacímét közli velünk.
Két kérdés merülhet fel:
- Honnan tudjuk hol a vége?
- Honnan tudjuk mennyit kell léptetni?
Teljesen mindegy hogy ASCII/ANSI kódolással van dolgunk kiolvasunk egy betűt, és léptetünk a címen 1 byteot. Unicode esetben erre nagyon oda kell figyelni hogy kettőt.
Szerencsére amint ezt látni fogjuk a puts(), printf(), stb... függvények ezt a léptetgetést elvégzik helyettünk és kiírják a képernyőre a szöveget.
A szöveg vége egy érdekesebb történet, itt többféle megoldás van - egyes programnyelvekben az első karakter nem is karakter hanem egy szám hogy milyen hosszú a szöveg; viszont a C/C++ megoldás más:
A szöveg mindig +1 karakterrel hosszabb mint kéne, és az utolsó karakter egy nullás indexű karakter. Pl. (ANSI):
| A | z | a | l | m | a | z | ö | l | d | . | |||
| 65 | 122 | 32 | 97 | 108 | 109 | 97 | 32 | 122 | 246 | 108 | 100 | 46 | 0 |
Ezen a módon a program addig írja ki a szöveget ameddig '\0' karaktert nem talál. Ez egy praktikus megoldás, de megint érvényes (lásd: A számítógép alkatrészei), hogyha rossz címet íratunk ki, vagy összeomlik a program, vagy '\0' híján hülyeségeket fogunk kapni, és nem áll le a kiírás.
Megadása (először kezdőértékkel, majd fix hosszal):
char* szoveg = "Alma";
char szoveg2[10];
A C/C++ alapvetően mindig ANSI módban dolgozik ha a char, char*, stb. változókkal dolgozunk és nem használunk speciális beállításokat.
10, A dátum/idő típusa
A dátum/idő tárolására is lehetőség van a C/C++ nyelvben, amihez a time_t típust lehet használni.
A tároláshoz a rendszer egy speciális valós számot használ, amiben az eltelt másodperceket jelöli 1970 január 1.-je, 0:00 óta. Nekünk ez első ránézésre tökéletesen haszontalan ám a gép remekül tud számolni vele.
A dátum típus használatához szükséges a time.h fájl (később lesz szó az ilyen fájlokról).
A dátum/idő tárgyalása nem célja ennek a leírásnak, az ezekkel kapcsolatos információk igény szerint itt megtalálhatóak (angol nyelven).
