Egyszerű dinamikus adatszerkezetek

A program elkészítése során gyakran találkozhatunk olyan esettel, hogy az adatok mennyiségét nem ismerjük a program írása közben, csak futásidőben.

Ilyen eset lehet pl. n darab szám átlagolása, ahol egy n elemű tömbben szeretnénk eltárolni a számokat - de hogy mennyi az n értéke azt a felhasználó fogja megadni futás közben. Az ilyen tömböt dinamikus tömbnek fogjuk nevezni a továbbiakban, míg az előző fejezetekből megismert tömböt statikus tömbnek.

Ez a fejezet azon adatszerkezetekkel foglalkozik, amelyeknek a mérete futásidőben állítható be, illetve igény szerint változtatható - de a kódbeli bonyolultság nem haladja meg túlzottan az eddigieket.

1, A dinamikus tömb, mint mutató
    1a, malloc
    1b, realloc
    1c, free
    1d, memset
    1e, A dinamikus tömb előállítása
2, A direkt struktúra alapú dinamikus tömb
3, A dinamikus mátrix
    3a, Miért kell két csillag?
    3b, A téglalapos dinamikus mátrix lefoglalása/felszabadítása
    3c, A szabadalakos dinamikus mátrix lefoglalása/felszabadítása
    3d, Az indirekt struktúra alapú dinamikus tömb
4, A dinamikus tér
5, A dinamikus n-dimenziós tömb
6, A C++ egyszerűsítései
    6a, A new/delete utasítás
    6b, std::vector

1, A dinamikus tömb, mint mutató

Mint ez már a fent megjelölt korábbi fejezetben említésre került, a tömb alapvetően egy mutató - ennek megfelelően azzal egyenértékűen helyettesíthető.

Továbbá az is említésre került a legelején, hogy a számítógép, mikor felveszünk egy változót, lefoglalja a neki szükséges memóriaterületet a változódeklaráció során. Ez a terület a sizeof(<típus>) operátorral kérhető le, byteokban.

Arról is esett szó hogy a tömb egy memóriafolytonos típus, vagyis az elemek egymás után következnek, így egy szorzással előállítható az n-edik elem címe.

Ezeket összevetve végül is arra lehet jutni, hogy a dinamikus tömb előállítható, ha megfordítjuk a változódeklaráció menetét:

lefoglalunk kézzel egy n * sizeof(<típus>) méretű területet a memóriában
ennek a területnek a címét eltároljuk egy mutatóban
és ezt a mutatót tömbként fogjuk használni

Lényegében ennyiről van szó, de mielőtt ezt kivitelezhetnénk, meg kell ismerkedni néhány utasítással - ezek a malloc, a realloc, a free, és a memset.

1a, malloc

void* malloc(unsigned int size);

A malloc lesz az a függvény ami a kézi lefoglalást végzi, és ha ez sikeres akkor a terület memóriacímét adja vissza.

size: azt adja meg, hogy mekkora legyen a lefoglalt terület mérete byteokban

A függvény visszatérési értéke a terület memóriacíme ha sikeres volt a foglalás. Egyéb esetben NULL.

Használata:

int elemszam = 25;
int* tomb = (int*)malloc(elemszam * sizeof(int));

Megjegyzés:
A malloc egy típusfüggetlen mutatót ad vissza (void* típus), amit ahhoz egy eltárolhassunk egy típusos mutatóban (pl. int* típus) át kell alakítani.
Ehhez típuskonverzióra van szükség, ami a memóriacímen magán nem változtat semmit, csak azon hogy a rendszer hogy kezelje mutatóként.
Erre az átalakításra főként C++ alatt van szükség, sima C esetében ez elhanyagolható (lásd alább). Ez abból adódik hogy a C++ egy erősen típusos nyelv, és ilyen árnyalatnyi különbségeken is fennakad, míg a sima C nem.

int* tomb = malloc(elemszam * sizeof(int)); //csak sima C alatt!

Fontos:
A malloc NULL értéket is visszaadhat. Mielőtt használnánk az általa elkészített változót, mindig ellenőrizzük le hogy a mutatónk értéke nem egyezik-e meg a NULL értékkel - különben a programunk összeomolhat.

Megjegyzés:
Egyes helyeken a malloc helyett a calloc használatát javasolják. Lényegében mindegy hogy melyiket választjuk, a callocnál két paraméter van, az első az elemszám, a második egy elem mérete - annyiban különbözik hogy nem mi szorozzuk össze ezt a két számot.
Én személyesen azért preferálom a malloc használatát, mert a callocnál szükséges az #include <stdlib.h> sor, is azaz egy plusz függvénytárat bele kell fordítani a programba. Ha más ok miatt nincs szükség erre a függvénytárra, akkor inkább használom a szorzásjelet a mallocnál - ezzel is kicsit optimalizálva a programot.

1b, realloc

void* realloc(void* ptr, unsigned int new_size);

A realloc egy már meglévő, kézzel lefoglalt memóriaterületet méretez át, egy megadott új méretre, miközben az ott tárolt adatokat megtartja.

ptr: a kézzel lefoglalt memóriaterület memóriacíme
new_size: az új méret byteokban

Mivel bizonyos esetekben ez nem vitelezhető ki ugyanazon a címen, ezért a realloc visszatérési értéke az átméretezett terület címe, ha sikeres a művelet. Egyéb esetben NULL.

Használata:

int elemszam = 25;
int* tomb = (int*)malloc(elemszam * sizeof(int));

...

elemszam = 30;
tomb = (int*)realloc(tomb, elemszam * sizeof(int));

Megjegyzés:
A fentebb leírt egyszerűsítésekkel, sima C alatt itt is lehet élni.

Fontos:
A realloc NULL értéket is visszaadhat. Mielőtt használnánk az általa elkészített változót, mindig ellenőrizzük le hogy a mutatónk értéke nem egyezik-e meg a NULL értékkel - különben a programunk összeomolhat.

1c, free

void free(void* ptr);

Egy kézzel lefoglalt memóriaterületet szabadít fel, ha már nincs rá szükség.

ptr: a kézzel lefoglalt memóriaterület memóriacíme

Az eljárásnak nincs visszatérési értéke.

Használata:

int elemszam = 25;
int* tomb = (int*)malloc(elemszam * sizeof(int));

...

free(tomb);

Fontos:
A free után a mutató érvénytelen lesz - és ezt már nem lehet leellenőrizni. A további hibák elkerülése végett, a free használata után, érdemes a mutatót átírni NULL értékre, így aztán egy sima feltételes utasítás ellenőrizheti az érvényességét.
Mindig szabadítsuk fel az összes kézzel lefoglalt változót a programból való kilépés előtt - a C/C++ ezeket nem számolja, így ha mi nem tesszük meg, akkor automatikusan sem fog megtörténni.

1d, memset

void* memset(void* dest, char ch, unsigned int count);

A memset egy tetszőleges memóriaterületet tölt fel mintázattal. Ez a mintázat úgy áll elő hogy a ch változó értékét, count alkalommal bemásolja az adott területre.

dest: a memóriaterület címe (nem csak kézzel lefoglalt lehet, lásd alább a példát)
ch: az a byte amiből a mintázat fog felépülni - lehet karakter, szám, stb.
count: az hogy hányszor másolja be a ch változót - mivel a ch 1 byte, úgy is értelmezhető hogy hány byte kerüljön átírásra

A visszatérési értéke a dest másolata, ha sikeres volt a művelet. Egyéb esetben NULL.

Használata:

char szoveg[] = "Ez egy teszt szöveg.";

memset(szoveg, 'a', 6); //szoveg == "aaaaaa teszt szöveg."

int elemszam = 25;
int* tomb = (int*)malloc(elemszam * sizeof(int));

memset(tomb, 0, elemszam * sizeof(int))

Megjegyzés:
A malloc szándékosan nem ad kezdőértéket a területnek, emiatt az ott található - más programok által otthagyott adatszemét lesz sokszor a kezdőérték.
Ha pl. azt szeretnénk hogy egy új tömb minden eleme nulla legyen, akkor a for ciklussal való feltöltés helyett a memset lényegesebben gyorsabban feltölti az területet nullákkal.

Fontos:
Ha a count nagyobb mint a terület, akkor a program össze fog omlani (túlfutás). Szintén ez a helyzet hogyha NULL értéket adunk meg a dest helyére.

1e, A dinamikus tömb előállítása

Most hogy láthattuk hogyan működnek ezek az függvények/eljárások, itt az ideje megnézni a gyakorlatban is hogy működnek.

Ez a legegyszerűbb példa, itt lefoglalunk egy 25 elemű tömböt (az n értéke lehetne más is - amit nem előre adunk meg), szórakozunk a tömb elemeivel, majd az egészet felszabadítjuk.

int n = 25;
int* tomb = (int*)malloc(n * sizeof(int));

tomb[0] = 12;
...
tomb[n - 1] = -15;

free(tomb);

A példából látható hogy az indexelés továbbra is [0..(n-1)] határok között mozog.

Habár ez javallott volt, a malloc sikerességének ellenőrzése elmaradt. Ez megtörténhet akkor, ha egészen kis elemszámú tömbökkel dolgozunk - egy mai gépben jó eséllyel van 25 * 4 = 100 byte ~ 0,1 kByte szabad memória.

Egy olyan esetben, ahol az elemszám nagyobb már mindenféleképpen kell védelem:

int n = 2500;
int* tomb = (int*)malloc(n * sizeof(int));

if (tomb != NULL)
{
tomb[0] = 12;
...
tomb[2499] = -15;

free(tomb);
}

A következő kérdés az lehet, hogy mi van ha az n értéke megváltozik a foglalás után?

A válasz hogy semmi. A tömböt akkor foglaltuk le, mikor az n értéke 2500 volt, vagyis attól még hogy átírjuk 3000-re, a tömb mérete nem fog megváltozni automatikusan - de megváltoztatható:

int n = 2500;
int* tomb = (int*)malloc(n * sizeof(int));

if (tomb != NULL)
{
tomb[0] = 12;
...
tomb[2499] = -15;

n = 3000;

tomb = (int*)realloc(tomb, n * sizeof(int));

if (tomb != NULL)
{
tomb[2999] = 0;

free(tomb);
}
}

Természetesen itt is ellenőrizni kell az új mutató helyességét, hiszen 3000 elemnél már előfordulhat hogy nem fog sikerülni az újrafoglalás.

Végül pedig, előfordulhat hogy egy olyan programot szeretnénk készíteni, ami tömbbe summáz bizonyoz értékeket.

Ekkor fontos lenne hogy kezdőértéke legyen, de ha minden elemre begépeljük hogy tomb[x] = 0 az nem hatékony - ezért ismerkedtünk meg a memsettel.

int n = 10, i, j;
int* tomb = (int*)malloc(n * sizeof(int));

memset(tomb, 0, n * sizeof(int));

for (i = 0; i < n; i++)
for (j = i; j < n; j++)
tomb[i] += (j + 1);

free(tomb);

A felszabadítás előtt ezen kód hatására a tömb állapota:

tomb[0] = 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
tomb[1] = 0 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
tomb[2] = 0 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
tomb[3] = 0 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
tomb[4] = 0 + 5 + 6 + 7 + 8 + 9 + 10;
tomb[5] = 0 + 6 + 7 + 8 + 9 + 10;
tomb[6] = 0 + 7 + 8 + 9 + 10;
tomb[7] = 0 + 8 + 9 + 10;
tomb[8] = 0 + 9 + 10;
tomb[9] = 0 + 10;

A memset hatása itt jelentős, hiányában a tömb értékei mind véletlenszerűek lennének - hisz nem a nulla kezdőértékhez adnánk a számokat, hanem valami zagyvasághoz.

2, A direkt struktúra alapú dinamikus tömb

Ez a témakör nem egy bonyolult dolog - lényegében ezúttal számok helyett struktúrákat pakolunk egymás után.

Ezeknek később a fájlkezelés során lehet nagy jelentősége, főként a direkt verziónak.

typedef struct
{
unsigned int eletkor;
char nev[50];
char lakcim[200];
float kedvenc_szam;
int szeme_szine, haja_szine, csaladi_allapot;
} TSzemely;

A séma ugyanaz mint tömbnél, de most int helyett TSzemely lesz.

int n = 35;
TSzemely* 3b_osztaly = (TSzemely*)malloc(n * sizeof(TSzemely));

if (3b_osztaly != NULL)
{
3b_osztaly[0].eletkor = 6;
...
3b_osztaly[34].nev = "Karcsi";

free(tomb);
}

Ezt nevezzük direkt struktúra alapú tömbnek, mivel a struktúráknak annyi hely kell folytonosan a memóriában, amekkora a struktúrák mérete. Egy struktúra mérete jelen esetben:

sizeof(unsigned int) + sizeof(char) * 50 + sizeof(char) * 200 + sizeof(float) + 3 * sizeof(int) =
4 + 50 + 200 + 4 + 12 =
262 byte

Ezáltal a teljes 35 elemű tömb mérete 35 * 262 = 9 170 byte. Ez nem sok egy mai gépen, de ha mondjuk egy egész iskola tanulóit vennénk számba, és 5 000 elemet vennénk fel = 1 310 000 byte ~ 1,3 MB.

Ez már lehet akkora méret hogy a malloc elhasal - hiszen ez folytonosan, megszakítás nélkül kéne. Ilyenkor fog bejönni az indirekt módszer (később).

Természetesen kis esetekben, mint ez a 35 simán jó ez a megoldás is, majd ezt később látni fogjuk hogy az indirekt módszer sokkal bonyolultabb.

3, A dinamikus mátrix

Mint az a statikus tömböknél ki volt fejtve, nagyjából úgy gondolnánk hogy egy n * k * sizeof(int) méretű tömb túlindexelése megoldás lehet. A valóságban a megoldás ennél egy kicsit komplexebb.

A két dimenziós mátrix lehet téglalap alakú, de nem kötelező hogy az legyen. A készítésekor az ún. "tömbben a tömb" eljárással fogunk dolgozni, ahol készítünk egy "tömbökből álló tömböt" - ami egy oszlopvektor, és ezen belül lesznek a sorvektorokat jelképező tömbök, amiknek a hossza nem kell hogy megegyezzen.

Íme egy standard, téglalapos mátrix dinamikus kivitele [7x6] (pl. int[7][6]):

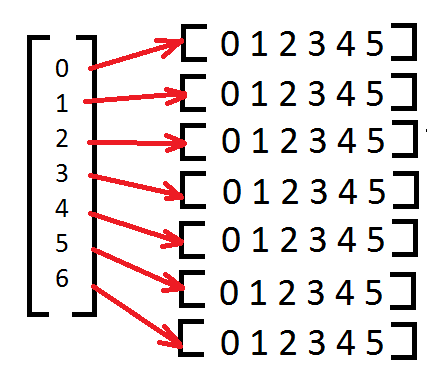
Illetve egy változó sorhosszú (szabadalakos) dinamikus mátrix kivitele [7x(3..10)]:

A statikus mátrixokkal ellentétben, itt valóban megvalósul a memóriabeli rendezettség, emiatt a túlindexelésre nincs lehetőség.

Amint az a képről is látható mindig az oszlopvektorból indul ki minden, vagyis először ennek a lefoglalását kell megkezdeni. Miután az oszlopvektor készen van nekiállhatunk a sorok előállításának - ez történhet fix mérettel (téglalapos mátrix), vagy algoritmus által (változó sorhosszú mátrix).

Természetesen a létrehozásnak nem ez az egyetlen módja, de ez követi a statikus változatnál megszokott elrendezést.

3a, Miért kell két csillag?

Azért van szükség két csillagra, mert tömb lesz a tömbben.

Ha megnézzük hogyan készül egy mátrix statikusan azt kapjuk hogy az

int matrix[6][7];

deklaráció egy 6x7-es mátrixot ad.

Ezt a deklarációt módosítsuk úgy, hogy a sorok dinamikus tömbök legyenek - ekkor lesz 6db tömbünk - vagyis az

int* matrix[6];

deklarációra jutunk.

Most pedig mondjuk azt hogy a sorok száma sem fix - így jön ki az

int** matrix;

deklaráció.

3b, A téglalapos dinamikus mátrix lefoglalása/felszabadítása

Vizsgáljuk meg az egyszerűbb esetet, mikor téglalap alakú a mátrix.

Elsőrendben tehát kell egy oszlopvektort készíteni, amibe a sorokat lefoglaljuk - ezt sorozatos malloc utasításokkal lehet előállítani:

int size_x = 10, size_y = 10, x, y;
int** matrix = (int**)malloc(size_y * sizeof(int*));

for (y = 0; y < size_y; y++)
matrix[y] = (int*)malloc(size_x * sizeof(int));

matrix[0][0] = 3;
matrix[9][9] = 1;

És felszabadítani:

for (y = 0; y < size_y; y++)
free(matrix[y]);

free(matrix);

Lényegében a felszbadítás során a sorokat szabadítjuk fel, majd végül magát az oszlopvektort miután végeztünk. Fordítva nem működne a dolog, hiszen az oszlopvektor tartalmazza a sorokat - anélkül a sorokat már nem tudnánk elérni.

A fenti példa egy egyszerűbb kivitel, ami megint csak korlátozott méretig működik. 10 * 10 = 100 elem lefoglalása történt meg ebben a példában, de mivel 10-es csoportokban, külön memóriaterületen vannak, ezért jó eséllyel elhanyagolható a védelem.

Nézzük meg egy 2 000 * 2 000 = 4 000 000 elemű mátrix dinamikus lefoglalását védelemmel:

int size_x = 10, size_y = 10, x, y, e;
int** matrix = (int**)malloc(size_y * sizeof(int*));

if (matrix != NULL)
{
for (y = 0; y < size_y; y++)
{
    matrix[y] = (int*)malloc(size_x * sizeof(int));

    if (matrix[y] == NULL)
    {
       for (e = 0; e < y; e++)
         free(matrix[y]);
       free(matrix);
       matrix = NULL;
       break;
    }
}
}

Ha hibába ütközik, minden addig lefoglalt sort visszafele intelligens módon felszabadít, majd végül az oszlopvektort, majd végül befejezi a ciklust, hogy ne történjen hiba.

Ez már egy komplex megoldás, erre csak nagy mátrixok esetén van szükség. A felszabadítás ugyanakkor ugyanúgy megy végbe mint a fenti példában.

Végül egy nullmátrix előállítása az alábbi módon történhet meg:

int size_x = 10, size_y = 10, x, y;
int** matrix = (int**)malloc(size_y * sizeof(int*));

for (y = 0; y < size_y; y++)
{
matrix[y] = (int*)malloc(size_x * sizeof(int));
memset(matrix[y], 0, size_x * sizeof(int));
}

matrix[0][0] += 3;
matrix[9][9] += 1;

A memset segítségével a sorokat fogjuk kinullázni - az oszlopvektor itt érdektelen, hiszen az a sorok memóriacímeit tartalmazza, kinullázásakor nem érnénk el többet a sorokat.

3c, A szabadalakos dinamikus mátrix előállítása/felszabadítása

Itt különösen fontos, hogy mindig tudjuk hogy az indexelés határai hol vannak.

Ha egy olyan sorban pl. ahol csak két elem van a harmadikra hivatkozunk, hibát kapunk, még akkor is ha van olyan másik sor ahol van harmadik elem.

int size_y = 10, x, y;
int** matrix = (int**)malloc(size_y * sizeof(int*));

for (y = 0; y < size_y; y++)
matrix[y] = (int*)malloc((y + 1) * sizeof(int));

A lényeg annyi hogy a size_x helyett valamilyen kifejezéssel számítunk sorhosszt, most jelen esetben size_x = y + 1.

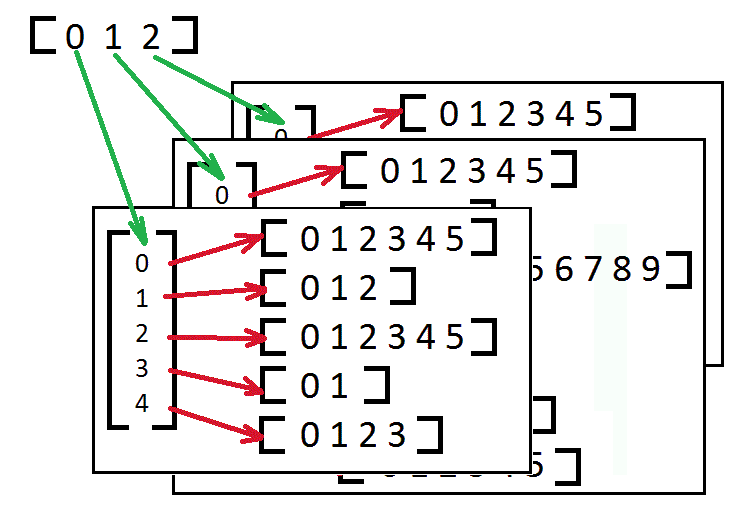
Az így kapott mátrix képe:

[0]
[0, 1]
[0, 1, 2]
[0, 1, 2, 3]
[0, 1, 2, 3, 4]
[0, 1, 2, 3, 4, 5]
[0, 1, 2, 3, 4, 5, 6]
[0, 1, 2, 3, 4, 5, 6, 7]
[0, 1, 2, 3, 4, 5, 6, 7, 8]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Az elemek mennyisége pedig:

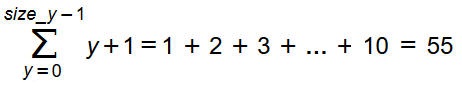
Ilyen esetben pl. a matrix[0][6] hibát okoz, míg a matrix[9][6] helyes lesz.

A felszabadítás ugyanaz mint a fentebbi példában, hiszen a free utasítást nem érdekli a sorok hossza, és a sorok száma pedig állandó.

for (y = 0; y < size_y; y++)
free(matrix[y]);

free(matrix);

Egy másik szabadalakos mátrix (ehhez már kell a math.h):

int size_y = 10, x, y;
int** matrix = (int**)malloc(size_y * sizeof(int*));

for (y = 0; y < size_y; y++)
matrix[y] = (int*)malloc((sin(y * M_PI / 2) + 2) * sizeof(int));

Íme a képe:

[0, 1]
[0, 1, 2]
[0, 1]
[0]
[0, 1]
[0, 1, 2]
[0, 1]
[0]
[0, 1]
[0, 1, 2]

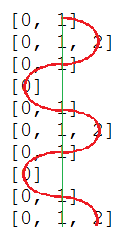És a számok mennyisége:

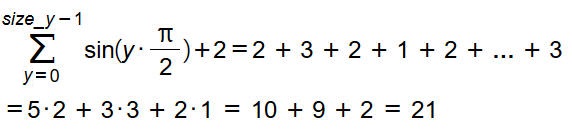
Az oldalsó szélét megnézve láthatunk egy szinusz hullámot - természetesen egy ilyen mátrixnak ritkán van értelme, de ki tudja...

Fontos:
Bármilyen képlettel is állítjuk elő a sorok hosszát, mindig győződjünk meg arról hogy a kapott érték mindig legyen nagyobb mint nulla! A malloc nem fog sem nulla, sem negatív területet lefoglalni, és később hibába futhatunk ezáltal.

3d, Az indirekt struktúra alapú dinamikus tömb

Képzeljük el hogy az oszlopvektorunk ezúttal nem sorvektorokra mutat, hanem struktúrákra - meg is kaptuk az indirekt struktúra alapú dinamikus tömböt.

Természetesen mivel több köze van a mátrixokhoz mint a tömbökhöz, lényegesen összetettebb lesz kivitelezni is mint a direkt verziót.

Előnye abban nyilvánul meg a struktúrák külön memóriaterületeken helyezkednek majd el, ezáltal nem muszáj nagy folytonos területeknek lennie, 5000 elem esetén sem fog elhasalni a malloc.

Az ilyen tömböknél ezen felül ki fogjuk használni a nyíl operátort is - ezért lesz indirekt ez a verzió, hiszen a struktúrához csak mutatónk van, nem érjük el közvetlenül.

int meret = 5000, n;
TSzemely** egesz_iskola = (TSzemely**)malloc(meret * sizeof(TSzemely*));

for (n = 0; n < meret; n++)
egesz_iskola[n] = (TSzemely*)malloc(meret * sizeof(TSzemely));

egesz_iskola[0]->eletkor = 12;
egesz_iskola[4999]->nev = "Zsoltika";

for (n = 0; n < meret; n++)
free(egesz_iskola[n]);
free(egesz_iskola);

4, A dinamikus tér

A tereknél is előállítható kocka alakú, illetve szabadalakos tér. Igazából a mátrixokra bevezetett tippeket kell továbbvinni csak, vagyis - vegyünk fel egy Z irányú lapvektort, aminek az elemei egy-egy (téglalapos/szabadalakos) mátrixra hivatkozhatnak.

A trükk most annyi, hogy az Y és X irányú összetevők is változhatnak (szabadalakos), és a Z lesz állandó.

Íme egy téglatest alakú elrendezés [3x7x6] (pl. int[3][7][6]):

Ezen megoldás elemszáma egyszerűen számítható - 3*7*6 = 126.

Továbbá egy szabadalakos elrendezés [3x(5..7)x(3..10)]:

Itt már az elemszám nem ilyen egyszerűen számítható, az egyes lapmátrixokat summázva kell összeadni az értékeket.

Mivel egy egy komplex dolog, mégis hasonlít a mátrixokra, egyetlen példa van itt - egy védelem nélküli, téglatest alakú tér lefoglalása, és felszabadítása:

int size_x = 10, size_y = 10, size_z = 10, x, y, z;
int*** ter = (int***)malloc(size_y * sizeof(int**));

for (z = 0; z < size_z; z++)
{
ter[z] = (int**)malloc(size_y * sizeof(int*));
for (y = 0; y < size_y; y++)
ter[z][y] = (int*)malloc(size_x * sizeof(int));
}

ter[0][0][0] += 3;
ter[9][9][9] += 1;

for (z = 0; z < size_z; z++)
{
for (y = 0; y < size_y; y++)
free(ter[z][y]);
free(ter[z]);
}
free(ter);

A felszabadításnál egy kis plusz nehézség, hogy az y irányú méretet is tudni kell - szabadalaknál ez gondot okozhat, hiszen az sem feltétlenül állandó.

5, A dinamikus n-dimenziós tömb

Mint azt az előzőekben láthattuk az alakzatok egymásra épülnek, vagyis egy 4D-s megoldásnál a terekből álló tömb lenne a megoldás, illetve 5D-nél a 4D-ből álló tömb stb...

Íme egy n-dimenziós szögletes tömböt foglaló rekurziv függvény:

void* nd_tomb(unsigned int* sizes, const unsigned int dimensions, const unsigned int element_size)
{
int n, size_n = sizes[dimensions - 1];
void** tomb;

if (dimensions = 1)
    return malloc(size_n * element_size);
else
{
    tomb = (void**)malloc(size_n * sizeof(void*));
    for (n = 0; n < size_n; n++)
      tomb[n] = nd_tomb(sizes, dimensions - 1, element_size);
return (void*)tomb;
}
}

Ez a függvény rekurzió által tetszőleges n-dimenziós tömböt fog lefoglalni (védelem nélkül, tehát csak kis méretű tömbökhöz alkamas).

sizes: egy tömb ami tartalmazza az adott dimenzióhoz tartozó méretet, pl. 3D esetén [0 = X, 1 = Y, 2 = Z]
dimensions: a méreteket tartalmazó tömb hossza, pl. 3D esetén 3; (amúgy meg > 0)
element_size: egyetlen elem mérete: pl. int esetén sizeof(int)

A visszatérési érték az n-dimenziós tömb, ha elég kevés iránnyal, és kis méretekkel dolgoztunk. Egyéb esetben a program összeomlik, a NULL értékű malloc kezeletlensége miatt. (a védett verzió jelentősen több kóddal járna, már egy mátrix esetében is kb. 2x-es volt a nagysága).

És végül pedig egy eljárás ami felszabadítja az n-dimenziós tömböt:

void nd_free(void* ptr, unsigned int* sizes, const unsigned int dimensions)
{
int n, size_n = sizes[dimensions - 1];
void** tomb = (void**)ptr;

if (dimensions > 1)
    for (n = 0; n < size_n; n++)
      nd_free(tomb[n], sizes, dimensions - 1);

free(ptr);

return;
}

ptr: a sikeresen lefoglalt n-dimenziós tömb memóriacíme
sizes: azok a méretek amivel a tömb le lett foglalva
dimensions: a méreteket tartalmazó tömb hossza (> 0)

Az eljárásnak nincs visszatérési értéke.

A függvények használatára is van egy példa, íme:

int 5d_meret[] = {5, 4, 3, 5, 2}; //600 elem
int***** 5d_tomb = (int*****)nd_tomb(5d_meret, 5, sizeof(int));

5d_tomb[0][0][0][0][0] = 2; //első elem
5d_tomb[1][4][2][3][4] = 5; //utolsó elem

nd_free(5d_tomb, 5d_meret, 5);

Természetesen ez az utasításpár alkalmas tömb, mátrix, illetve tér lefoglalására is.

Ugyanakkor egy tömb lefoglalása ezek által elég értelmetlennek tűnhet - hiszen tömbben kell megadni azt az egy méretet amit le kell foglalni, de képes rá.

Arra kell odafigyelni a használatakor, amint az a példából látható, hogy a legnagyobb elem koordinátái megfordulnak (a hosszokat tartalmazó tömböt pl.{X, Y, Z} alakban kell megadni, de ekkor indexelni már [z][y][x] alakban kell).

Ezen felül, a beadandó feladatokhoz is remekül használhatóak, sőt jól terjeszthető utasítások ezek ha pl. a tanult módon .H + .C fájlt készítünk belőlük. Sok beadandó mátrixfoglalásokat kér, viszont ez a két utasítás rövidre zárja a témát - minimális kóddal lesz megvalósító a feladat.

6, A C++ egyszerűsítései

A C++ nevében azért van két plusz jel, mert többet tud mint idősebb társa. Ezen leírás példái csakis C++ nyelv alatt fognak működni. Ahhoz hogy ezekkel az egyszerűsítésekkel tudjunk dolgozni, szükséges a fentebbi ismeretek elsajátítása.

6a, A new/delete utasítás

Mindez szép és jó amivel eddig foglalkoztunk, de a C++ nyújt ezekre a problémákra gyorsabb megoldást is:

A new utasítás a malloc szerepét tudja kiváltani lényegében, lefoglal egy n elemű tömböt. Íme:

int* tomb = new int[20];
tomb[24] = 50;

A delete utasítás pedig a free helyére lép:

delete [] tomb;

Használatukhoz kell a

#include <new>

sor is. Ezek segítségével a korábbi példák is újraértelmezhetőek.

A jó hír hogy egyfajta védelmet is kapunk, ugyanis a program hiba esetén kivételt dob fel (try-catch blokk később), amit okosan lehet kezelni.

A hátránya az ilyen tömböknek hogy átméretezni nem lehet őket, mint a fenti megoldásnál a realloc segítségével tettünk.

6b, std::vector

Az std::vector egy objektum (elöljáróban annyi hogy egy olyan struktúra aminek utasításai is vannak). A lényege hogy a tömböket helyettesíti ki, nagyon okos módon.

Egyrészt mindent amit a tömb tudott, azt tudja ez is, - az átméretezést is beleértve.

Használatához kell a

#include <vector>

sor is.

Nézzük meg egy egyszerű tömböt hogyan helyettesít ki:

std::vector<int> tomb(25);
tomb[24] = 50;

Felszabadítására nincs szükség, a rendszer elvégzi magától.

Ha több/kevesebb elemre van szükségünk:

tomb.resize(60);
tomb[59] = 50;

A legszebb hogy minden védve történik itt is, kivételek által.

Az std::vector ennél sokkal többet is tud, pl. elemek beszúrása, egy adott indexre. Ehhez tömböknél kellett volna egy realloc, illetve át kellett volna helyezni az elemeket, eggyel odébb.

tomb.insert(10, -5);

Ennek a sornak a hatására, a tömb most már 61 elemű, és a tomb[10] == -5

Szintén extra tudás az elem törlése is, ez is komoly fejfájást okozhat egy egyszerű tömbnél:

tomb.erase(10);

Akár egész szakaszok is törölhetőek (10..14-ig töröl mindent):

tomb.erase(10, 15);

Ha pedig csak hozzá akarunk adni egy elemet a végére:

tomb.push_back(-7);

Ha valami oknál fogva úgy lenne rá szükségünk mint egy sima tömbre:

int* sima_tomb = &tomb[0];

Az std::vector alkalmas mátrixok létrehozására is, manipulátor műveleteivel pedig a szabadalak is könnyen kezelhető.

std::vector<std::vector<int>> matrix; //nem kötelező a méret

matrix.resize(7); //7x10

int y;
for (y = 0; y < 7; y++)
matrix[y].resize(10);

matrix[0][0] = 7; //legkisebb
matrix[6][9] = 4; //legnagyobb

matrix[6].erase(9); //az utolsó sor utolsó elemének törlése
matrix.erase(6); //az egész utolsó sor törlése