A programozás során természetesen előfordulhat hogy az alapvető típusok (mint az int, float, ...) nem nyújtanak számunkra elég lehetőséget, vagy sokkal nehezebben kivitelezhető programot adnak eredményül.
Ilyenkor lehetőségünk van ún. egyedi típusok alkalmazására - amiknek mi adjuk
meg a jellegét - természetesen az alaptípusokra építkezve.
1, Tömb/vektor
1a, Mátrixok
1b, A tér
1c, Tetszőleges n
dimenziós tömb
2, Struktúra
2a, Típusdefiníció
2b, A struktúrák felvétele
2c, A struktúramutató
2d, Union
2e, Flexibilis struktúra
3, Az enumeráció
4, Álnév (alias)
5, Halmazok
5a,
Halmazelemekkel kapcsolatos műveletek
5b, Halmazok közötti
műveletek
1, Tömb/vektor
Legyen a feladat 100db szám kiátlagolása. Ebben az esetben az már egy jó gondolat hogy for ciklussal hajtsuk végre az összegzést, de a számok tárolása kérdéses lehet - pl. vegyünk fel 100db változót így: int a1, a2, a3, ... ? Ennek semmi értelme nem volna, hiszen a for ciklusban nem tudnánk használni a nevüket ilyen módon. Erre nyújt megoldást a tömb.
A tömb logikája hogy egymás utáni memóriaterületekre azonos típusú változók kerülnek - a tömb pedig az első memóriacímét takarja (legyen P). Mivel tudjuk hogy egy mérete pl. 4 byte - ha a 25.-dik elemre van szükségünk akkor annak a címe:
[25. elem címe] = P + 4 * (25 - 1)
[1. elem címe] = P
Azért kell kivonni egyet, mert már ha az 1.-nél állunk akkor 1 + 25 = 26. De ennek van egy más megközelítése is, ami számunkra érdekesebb - a C/C++ megközelítés:
Kezdjük el az elemeket nullától számozni, így a [25. elem] igazából a 26.-dik lesz, de ez majd lényegesen egyszerűsíti a dolgunkat, és a programozó meg majd számol nullától:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25] -> ez 26 db számjegy
[25. elem címe] = P + 4 * 25
[0. elem címe] = P
Ezek után belátható hogy a C/C++ nyelvben miért lesz a tömb mindig nullától indexelt. A műveleteknél már elöljáróban ismertetve lett a tömb operátora - ám példa nem volt rá. Íme akkor egy tömbdeklaráció és a fentebb említett példa:
| int
tomb[100], i; float atlag = 0; for (i = 0; i < 100; i++) atlag += tomb[i]; atlag /= 100; |
A példában a for ciklus az i számot 0-99 értékek között növeli, és a tömb [i. dik elemét] hozzáadja az átlaghoz. Ez után hogy tényleg átlag legyen leosztja 100-zal az eredmény, mivel 100 számot adtunk össze.
Tömbökből is lehet konstansot készíteni, illetve lehet nekik kezdőértéket adni, pl.:
| const
int szamok[]
= {0,
1,
2,
3,
4}; int tomb[100] = {0}; |
Az első példa esetében nem adtuk meg az elemszámot - ilyenkor ezt a C/C++
eldönti magától (kezdőérték esetén csak).
A második példa a tömb mind a 100 elemét ki fogja nullázni - így is lehet
kezdőértéket adni.
Mivel a tömb lényegében egy szám n-es, ezért vektornak is hívják - pl. egy float v[3] = {-1, 2, 0} valóban remekül reprezentálja a tér egy vektorát.
A C/C++ nyelvben a tömb ~= a mutatóval is. Mint ezt már korábban láthattuk a szöveg tárolásánál, a szöveg egy char[...] változó, de ha nem ismerjük a hosszát akkor char*. Ennek ellenére mind kettő indexelhető a fentebb látható módon, illetve mind a kettőn működnek a mutatóműveletek. Ez később fontos lesz a dinamikus tömböknél.
Bárhogy is használjuk a tömböket oda kell figyelni a túlindexelésre. A tomb[-1]
és a tomb[100] memóriahibát fog okozni, mivel olyan területre kér hozzáférést
amire a programnak nincs (védett
mód) - így a programot vagy bezárja az operációs rendszer, vagy kivételt
generál benne. A C jellemzője az előbbi, a C++ jellemzője az utóbbi - egyik sem
nyerő a programra nézve.
Mindig figyelni kell tehát hogy csak a határok között dolgozzunk a tömbbel
([0..99] a példában).
Megjegyzés: Mivel a tömb memóriafolytonos, és összecserélhető a mutatóval érvényesek, és ekvivalensek lesznek az alábbi műveletek:
| int tomb[100]
= {0}; int* tomb_mutato = tomb; if (tomb[97] == *(tomb_mutato + 97)) tomb_mutato[97] = *(tomb + 97); |
Ez a pár sor nem csinál semmit, csak szórakozik a tömb különböző hivatkozásaival.
Amikor felvesszük a mutatót, azért nem kell az & jel a tomb elé, mert az már önmagában véve egy mutató.
A (tomb_mutato + 97) azt jelenti hogy 97 * sizeof(int) értékkel tolja el a tomb_mutatoban lévő memóriacímet - mintha indexelnénk, így következésképpen meg kell egyeznie a tomb[97]-nek a (tomb_mutato + 97) címen lévő elemmel, ami a *(tomb_mutato + 97).
Mivel ez úgyis teljesülni fog, az alsó sor arra mutat példát, hogy annyira ekvivalens a mutató, és a tömb a C/C++ nyelvben, hogy a két megadási mód fordítva is használható.
Ez a kódrészlet csak a hivatkozásokat mutatja be, a tomb elemei nem fognak változni.
1a, Mátrixok
A mátrix lényegében egy számhalmaz, ahol a számokat x oszlopba és y sorba rendezzük. pl. (x = 3, y = 4):
| 5 | 6 | 2 |
| -1 | 4 | 2 |
| 0 | 3 | 1 |
| 2 | 4 | -5 |
A C/C++ ilyen adatszerkezet kialakítására is képes - mindössze két tömböt kell használni egymásban:
"egy olyan tömböt, aminek az elemei számokból álló tömbök"
Ez után akkor nézzünk erre is egy példát:
| int
szamok[4][25],
x, y; //4 * 25 = 100 float atlag = 0; for (y = 0; y < 4; y++) for (x = 0; x < 25; x++) atlag += tomb[y][x]; atlag /= 100; |
Tippek a mátrixokhoz:
-
Mindig [sor][oszlop] alakban adjuk meg őket - mind deklarálásnál, mind a hivatkozásnál
-
Mivel [sor][oszlop] szerkezetet használunk, ezért mindig a [sor] for ciklusa van kívül, és az [oszlop] for ciklusa van belül
-
Célszerű [y][x] koordinátákkal jelölni az irányokat, mint a koordináta-rendszer tengelyeit
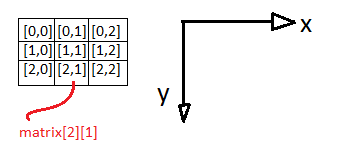
Végül néhány konstansmátrix:
| int
szamok[2][3]
= {{1, -2, 3} {4, 5, -6}}; int szamok[2][3] = {1, -2, 3, 4, 5, -6}; int szamok[2][3] = {0}; |
A második példa azt mutatja meg hogy a mátrix lényegében csak elvi síkon 2D-s, valójában a memóriacímzésből adódóan csak is 1D-s lehet, mint a tömb:
Mátrix[Y][X] = P + Y * Szélesség + X
Ez lényegében a tömb képlete, csak most az indexet két számból állítjuk elő:
Index = Y * Szélesség + X
Ez úgy jön ki hogy ahhoz hogy az [Y][X]-dik elemhez eljussunk először végig kell menni Y soron, amelyben soronként annyi elem van amennyi a mátrix szélessége + még el kell jutni az X-dik elemhez is. A nullától indexelés kiküszöböli majd itt is az elcsúszásokat - hiszen ha Y=0, X=0 akkor Index = 0, vagyis Mátrix[0][0] = P.
A képletekből viszont az is következik hogyha a határokon átlépünk egy elemet máshogy is eléhetünk:
Mátrix[1][1] = Mátrix[0][4]
- de mint az a tömböknél már előkerült a túlindexelés akár hibákhoz is vezethet a védett mód miatt, a
Mátrix[2][3]
hivatkozás is összeomlasztja a programot. A fentebbi példa azért volt jó viszont mivel a képlettel számolt érték beleesik a mátrixnak, mint tömb, a határaiba - a másik viszont kiesik ebből:
- ha tömb lenne 2*3=6 eleme lenne
- tömbként az indexelése 0..5-ig történne
- első példa: 1*3+1 = 0+4 = 4 <= 5
- második példa: 2*3+3 = 9 > 5, így hiba fog történni
1b, A tér
A tér egy olyan mátrix amelynek az elemei tömbök. Mivel most már három koordináta kell az elem meghatározásához térbeli alakzatról beszélhetünk, méghozzá egy kockáról aminek 3x3x3 esetben 27 pontjában lesz szám (3 lap, laponként 9).
A tér még nem a legvége a dolgoknak de minden ami a mátrixra érvényes volt érvényes ide is kissé kiterjesztve.
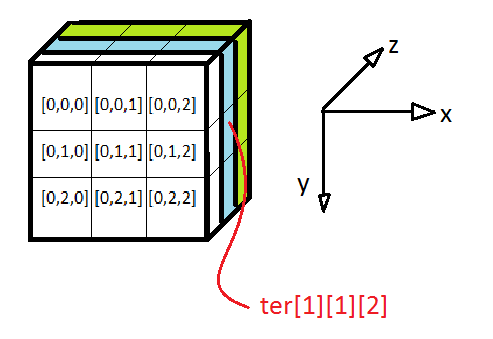
Index = Z * Szélesség * Magasság + Y * Szélesség + X
Tér[Z][Y][X] = P + Index
Mind a túlindexelésre, mind a for ciklusokkal való használatára mind a konstansokra a fentebb megtett javaslatok és megállapítások érvényesek.
1c, Tetszőleges n dimenziós tömb
A tömbök egymásba ágyazása közel a végtelenségig lehetséges. Íme általános esetre néhány megoldás (legyenek a tengelyek x1, x2, ..., x{n-1}, xn).
Index =
XN * Méret(X{N-1}) * ... * Méret(X2) * Méret(X1) +
X{N-1} * Méret(X{N-2}) * ... * Méret(X2) * Méret(X1) +
... +
X2 * Méret(X1) + X1
Tömb[XN][X{N-1}]...[X2][X1] = P + Index
Mind a túlindexelésre, mind a for ciklusokkal való használatára mind a konstansokra a fentebb megtett javaslatok és megállapítások érvényesek.
2, Struktúra
Képzeljük el hogy szükségünk van egy evőeszköz készletre. Mikor kibontjuk a dobozt lesz benne pohár, villa, tányér, kanál - de egyik sem egyforma méretű, így a doboz különböző méretekre van osztva.
A programozás során is előfordulhat hogy ilyen gyűjtőre lenne szükségünk de a tömbök ezt nem egészen írják le jól - csak azonos változóból állhatnak. Ilyenkor jön be a struktúra.
Ahhoz hogy az evőeszköz készletet bedobozolhassák, szükség van egy tervrajzra. Ezen a tervrajzon rajta van hogy hol kell behajtani a kartont, mekkora az egyes eszközök mérete, mekkora lesz a doboz ha elkészült. Ez a struktúránál sincs máshogy - csak itt a tervrajz helyett a típusdefiníció lesz ami leírja annak az alakját.
2a, Típusdefiníció
Mikor struktúrát készítünk ténylegesen szükségünk lesz egy új típusra, aminek a leírása itt adható meg. Példaképp nézzük meg hogy hogyan lehet leírni egy személy adatait struktúrával:
| typedef
struct { unsigned int eletkor; char nev[50]; char lakcim[200]; float kedvenc_szam; int szeme_szine, haja_szine, csaladi_allapot; } TSzemely; |
Mikor végeztünk a típusdefinícióval:
- még egy változónk sincs, csak egy "tervrajzunk"
- amit megadtunk nevet, az az új típusnak lesz a neve (TSzemely) - amivel majd változókat gyárthatunk
Tipp:
- Az elnevezési konvenció alapján az alaptípus "T" (type)
betűvel kezdődik, míg az alaptípusból készült mutató "P" (pointer)
betűvel kezdődik. A példa ilyen átirata (ez után már egyből lesz
mutató típusunk is):
- ... } TSzemely, *PSzemely;
- Bár ez nem jelent meg a példában, de érdemes olyan
mezőneveket használni ami mutatja annak a típusát is, pl.:
- iEletkor, szNev, szLakcim, fKedvencSzam, iSzemeSzine, iHajaSzine, iCsaladiAllapot
2b, A struktúrák felvétele
Ha már elkészítettük a TSzemely típusunkat, vegyünk fel változókat ilyen formán:
| TSzemely Jani, Sanyi, Pista, 3b_osztaly[25]; |
Most felvettünk három személyhez változókat - Jani, Sanyi és Pista nevű változókba, illetve egy egész osztályhoz adatokat 25 fős létszámhoz igazítva (tömb által). Most már csak adatokkal kéne feltölteni ezeket.
Az adatok feltöltését megtehetjük előre megadott konstansként, illetve futásidőben [mindkét esetben az előre beharangozott "." operátor lesz a segítségünkre]:
|
TSzemely Jani = { .eletkor = 12, .nev = "Kovács János", .lakcim = "Kukutyin, Kossuth utca 5.", .kedvenc_szam = 3.14, .szeme_szine = 1, .haja_szine = 2, .csaladi_allapot = 0 }, Sanyi = {/*... mint az előbb ... */}, Pista = {/*...*/}, 3b_osztaly[25] = {{/*...*/}, {/*...*/}, /*... még 21 elem leírása ...*/, {/*...*/}, {/*...*/}}; |
A struktúrának a változói mezőknek hívjuk, ezeket a mezőket pedig elérhetjük a "." operátorral futásidőben is:
| int
osszeg = 0, i; float atlag; osszeg += Jani.eletkor; osszeg += Sanyi.eletkor; osszeg += Pista.eletkor; for (i = 0; i < 25; i++) osszeg += 3b_osztaly[i].eletkor; atlag = osszeg / 28; |
Természetesen írni is lehet a mezőket, nem csak olvasni:
| 3b_osztaly[24].eletkor = 13; |
A struktúráknak később a fájloknál nagyon nagy haszna lesz, mivel ha a mezői között nincsen mutató - az összes mezejét egy sorban le lehet menteni, vagy kiolvasni a fájlból.
2c, A struktúramutató
Természetesen ha már új típusunk van a mutatóképző operátorral ebből is készíthetünk mutatót. Ez még a dinamikus struktúra alapú tömböknél fog előjönni.
| TSzemely* Peti = &(3b_osztaly[4]); |
Most azt mondjuk hogy Peti a 3b osztály 5. személye. Ilyenkor mivel ez egy mutató két módon érhetjük el a mezőket:
| (*Peti).eletkor =
5; Peti->eletkor = 5; |
Erre való a nyíl operátor.
Érdekesség:
A Peti változó most csak egy mutató - egy memóriacím,
méghozzá a (3b_osztaly[4]) címe.
Ebből kifolyólag ha olvassuk/írjuk azt a változót amire a
Peti mutat (fentebbi példa mindkét esete) - akkor a 3b_osztaly[4] változót
írjuk/olvassuk, mivel oda mutat.
Ez a mutatók lényege, de erről majd később még lesz szó.
2d, Union
Az union definiálása szinte semmiben sem különbözik a struktúráétól, de sok különböző méretű típus esetén kevesebb memóriát fog foglalni mint a struktúra. Ez azért következhet be, mivel itt megszünteti azt a néhány byte hézagot ami felléphet.
Ez a hézag abból adódik, hogy a struktúra esetén a evőeszközös dobozt úgy készítem el hogy a tányérhoz méretezek minden rekeszt, elvégre akkor minden ami kisebb mint a tányér belefér a saját rekeszébe.
Az union ezzel szemben minden rekeszt a maga méretéhez készít el, ezzel csökkentve a kihasználatlan helyeket.
Definiálása:
| typedef
union { char szoveg[20]; int szam; float valos; } TUnion; |
2e, Flexibilis struktúra
A struktúra és az union kombinálásával megszülethet a flexibilis struktúra:
| typedef
union { char bA, bR, bG, bB; } TARGBQuad; typedef union { unsigned long int ullSzin; } TARGBSzin; typedef struct { union { TARGBQuad aqErtekek; TARGBSzin asKombinalt; }; } TARGB; |
1,
Itt az történt hogy készítettünk egy olyan struktúrát amivel ugyanazt a memóriaterületet más részekre oszthatjuk.
Ha az aqErtekek mezőt használjuk a bA, bR, bG, bB négy darab byte-ot jelöl, amik egy átlátszó szín összetevői (alpha, red, green, blue).
Ezek egyenként nem alkalmasak egy szín meghatározására, csak együtt - méghozzá úgy ha a 4 byte sorban így van mint a TARGBQuad-ban.
Mi van akkor ha nekünk ez a 4 byte egyben kéne (mint HTML-színkód pl.)? Ekkor az asKombinalt mezőt használjuk, ami ugyanarról a területről most a külön-külön lévő 4 byte-ot összeollózza, és egy számban engedi kiolvasni.
Fordítva is működik a dolog, ha az asKombinalt.ullSzin = 0xFF7FC724 színkódot beírjuk ebbe a 4 byteba, az aqErtekek mezőben kiolvashatjuk az egyes színösszetevők nagyságát, pl. aqKombinalt.bA == 255, aqKombinalt.bR = 127, ...
Mivel ugyanazt az adathalmazt többféleképpen módosíthatjuk, ezért lesz ez a struktúra flexibilis.
2,
Ha nem fontos hogy a mezők egymást fedjék akkor az union-ban lévő típusok lehetnek struktúrák is, pl. MSDN - ekkor nem fogják a mezők egymást fedni, vagy az egyik lesz egyszerre, vagy a másik.
Ez is flexibilis, de itt már nem olvashatjuk ki ugyanazt a területet másféleképpen.
3, Az enumeráció
Mi van akkor ha sorszámozott típusra lenne szükségünk, de nem számra? Ekkor jön képbe az enumeráció ami a struktúrához hasonlóan típusdefinícióval kezdődik.
Ennek pl. akkor van haszna ha a TSzemely struktúrában a haja_szine változót szám helyett, értelmes tartalommal szeretnéd felruházni. Íme hát néhány enum típus:
| typedef
enum { ssBarna, ssKek, ssZold, ssFekete } TSzemSzin; typedef enum { caKapcsolatban = 1, caEgyedulallo = 0, } TCsaladiAllapot; typedef enum { hsEgyeb = hsBarna = 0, hsFekete, hsSzoke, hsVoros } THajSzin; |
A szám jellege továbbra is megmarad egy ilyen típusnak, de a szám most mégis index jellegű - és a név által tartalmat kap.
Az enum mezői is nullától számozódnak kivéve ha mást adsz meg:
- ha nincs megadva semmi, akkor az első érték a 0, a következő 1, és így tovább. (1)
- ha mind megvan adva, az a mérvadó - teljesen random sorrendben is lehetnek a számok, nem csak növekvőben (2)
- ha megvan adva egy érték, de más nincs, akkor az az lesz aminek meg lett adva, és a többit ahhoz képest számozza. (3)
Példa:
|
THajSzin haj1 = hsBarna; haj1++; /* most már hsFekete */ haj1 += 2; /* most már hsVoros */ |
Tippek:
- Az elnevezési konvenció alapján az alaptípus "T" (type) betűvel kezdődik, míg az alaptípusból készült mutató "P" (pointer) betűvel kezdődik.
- Az enum mezői általában a típus rövidítésével kezdődnek - így egyértelmű hogy melyik enumból való az érték, valamint az automata kiegészítésnél elég begépelni hogy "hs" és máris kiadja a gép az össze hajszín variációt.
4, Álnév (alias)
Az álnév során egy már létező típusnak adunk új nevet pl.:
| typedef unsigned char byte; |
Mostantól az unsigned char típus byte néven is ismeretes:
| byte bSzam = 127; |
Az alias segítségével készíthetőek mutatók is, tömbök is mint új típus:
| typedef
byte* PByte; typedef char TSzoveg[255]; |
Sőt akár még függvényekhez is készíthetünk velük mutatót (későbbiekben):
| typedef float (*TFuggveny)(float); |
Habár ez most csúnyának tűnhet, lényegében egy sima függvénydeklaráció ahol a függvény nevét (*fv_név) alakban írtuk be, és a bekért adatoknak nincs neve. A függvényekkel foglalkozó témakör sok dologra rávilágíthat majd még ezzel kapcsolatban.
5, Halmazok
Ez is egy könnyed témakör mint a tömb vagy a struktúra. Megismeréséhez szükséges a bitenkénti logikai operátorok megértése.
A C/C++ halmaz esetén annyi elemünk lehet egy halmazban, ahány bites a gép. Ez abból adódik hogy minden egyes bitet, úgy fogunk kezelni egy pl. 32-bites számban, mint egy-egy logikai típust, melyek megadják hogy az adott elem benne van-e a halmazban.
1,
Tehát először is készítsünk el egy enumot, a halmazelemek megadásával - vonatkozzon pl. egy betűtípusra stílusára:
| typedef
enum { bsFelkover = 1, bsDolt = 2, bsAlahuzott = 4, bsAthuzott = 8, bsAlsoIndex = 16, bsFelsoIndex = 32, bsKiskapitalis = 64, bsNagykapitalis = 128 } TBetuStilus; |
Bizonyára feltűnt hogy a kettő hatványait kellett használni a számérték megadásakor. Ez azért van mert így a számértékek bináris rendszerben mindig csak egy helyiértéken lesznek 1-esek a többin mind 0.
pl.:
bsFelkover = 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0001
bsDolt = 0000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0010
bsAlahuzott = 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0100
bsAthuzott = 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 1000
bsAlsoIndex = 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
0000 0001 0000
és így tovább, és így tovább...
Mivel kettes számrendszerben jól ábrázolható az alak, ezért szokás 16-os számrendszerben felírni a számokat (2^16 után már nagyon használhatatlan a decimális alak):
| typedef
enum { bsFelkover = 0x00000001, bsDolt = 0x00000002, bsAlahuzott = 0x00000004, bsAthuzott = 0x00000008, bsAlsoIndex = 0x00000010, bsFelsoIndex = 0x00000020, bsKiskapitalis = 0x00000040, bsNagykapitalis = 0x00000080 } TBetuStilus; |
Így már egész jól átlátható.
2,
A halmaz típusa nem lesz más mint egy alias:
| typedef unsigned long int TBetuStilusok; |
Megjegyzés: Érdemes megfigyelni itt is az elnevési trendet.
3,
A halmazunk készen áll a bevetésre:
-
lesz egy egész előjel nélküli számunk
-
bitenkénti logikai műveletekkel ki/betehetünk elemeket
-
feltételes utasításban és művelettel ellenőrizhetjük hogy azok benne vannak-e a halmazban
5a, Halmazelemekkel kapcsolatos műveletek
Vegyük azt hogy a halmazunk ismeretlen binárisan, de szeretnénk beletenni egy elemet, pl. a bsFelkovert:
A megfelelő művelet az lesz ami, a többi részen megkíméli az eredeti állapotot - de a bsFelkover szükséges bitjét átírja. Ez nem lesz más mint a vagy művelet (és itt most fontos hogy a sima "|" jelet használjuk - a "||" logikai típusokhoz van fenntartva).
bsHalmaz = ???? ???? ???? ???? ???? ????
???? ???? ???? ???? ???? ???? ???? ???? ???? ????
bsFelkover = 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0001
eredmény = ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???1
A vagy művelet ahol alul egy darab egyes van ott átírja egyre a bsHalmazt (?|1->1), a többi helyen pedig hogyha két nulla volt - nulla marad (0|0->0); ha az eredetiben egyes volt - egyes marad (1|0->1).
| bsHalmaz = bsHalmaz | bsFelkover; |
Most nézzük meg azt hogyan lehet kivenni egy elemet a halmazból pl. a bsDoltet:
Ehhez két művelet kell alternálás, és az és:
bsHalmaz = ???? ???? ???? ???? ???? ????
???? ???? ???? ???? ???? ???? ???? ???? ???? ????
~bsDolt = 1111 1111 1111 1111 1111 1111 1111 1111 1111
1111 1111 1111 1111 1111 1111 1101
eredmény = ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???? ???1
Ahol egyes volt, ott egyes marad az eredeti (1&1->1), ahol nulla volt az eredeti ott nulla marad (0&1->1), ahol pedig a ~bsDolt lesz nulla ott az eredetiből el kell hogy tűnjön az egyes ha volt egyáltalán (?&0->0, a második feltétel nem teljesül alapból).
| bsHalmaz = bsHalmaz & ~bsDolt; |
Most pedig nézzük meg hogyan lehet leellenőrizni hogy egy adott elem benne van-e a halmazban:
Most az és művelet lesz a segítségünkre:
bsHalmaz = ???? ???? ???? ???? ???? ????
???? ???? ???? ???? ???? ???? ???? ???? ???? ????
bsAlahuzott = 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0100
eredmény = 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0?00
Mindenhol ahol nulla van a bsAlahuzottban, ott úgyis nulla lesz (?&0->0), de ahol egyes volt benne ott még megvan a lehetősége hogy más szám is legyen (?&1->?). Ha ott a kérdésésen helyen egyes volt (1&1->1) az eredmény a bsAlahuzott lesz önmaga, de ha ott nulla volt (0&1->0) akkor az eredmény is csupa nulla -> számszerűen is nulla lesz:
| if
(bsHalmaz & bsAlahuzott !=
0) { ... }; if (bsHalmaz & bsAlahuzott == bsAlahuzott) { ... }; |
Mint arról szó esett az alaptípusoknál minden ami nem nulla az igaz, tehát az if-be ennyit kell írni:
| if (bsHalmaz & bsAlahuzott) { ... }; |
5b, Halmazok közötti műveletek
Lényegében mindent elvégeztünk egy-egy elemre, de az előző logikából kiindulva ezek kombinálhatóak is:
| bsHalmaz = bsFelkover | bsAlahuzott | bsDolt & ~bsKiskapitalis; |
Ehhez semmi mást nem kell, csak a logikai tábláknál, több 1/0 lesz attól függően hogy éppen mi kell nekünk - az eredmény ugyanaz lesz - ezúttal több elemmel egyszerre.
Egy ilyen sort csak ki kell olvasni:
"bsHalmaz egyenlő bsFélkövér, vagy bsAláhúzott, vagy bsDőlt, de nem lehet bsKiskapitális"
Megjegyzés: programozási szempontból az "és", és a "de" kulcsszó között nincs különbség.
Az előzőekből kiindulva már könnyen belátható hogy:
- Két halmaz uniója: H = H1 | H2
- Két halmaz metszete: H = H1 & H2
- Két halmaz különbsége: H = H1 & ~H2
- Két halmaz egyenlősége: if (H1 = H2) { ... }
- Két halmaz részhalmazúsága: if (H1 & H2 == H2) {...}
Megjegyzés: Itt kell hogy egyenlő H2-vel: ha nem részhalmaza, de néhány elem közös akkor az eredmény a közös elemeket fogja tartalmazni és nem a nullát.
hiszen ha az elemekre összevonhatóak a műveletek, azaz több elemmel egyszerre lehet elemműveletet végezni, akkor lényegében a halmaz elemek gyűjteményeként, egy az egyben vonható ki/adható össze, stb.
Innen kiindulva viszont az enumba úgymond kész részhalmazokat is fel lehet venni:
| typedef
enum { bsFelkover = 0x00000001, bsDolt = 0x00000002, bsAlahuzott = 0x00000004, bsAthuzott = 0x00000008, bsAlsoIndex = 0x00000010, bsFelsoIndex = 0x00000020, bsKiskapitalis = 0x00000040, bsNagykapitalis = 0x00000080, bsKitevo = 0x000000A0, //bsNagykapitalis | bsFelsoIndex bsKisatirozott = 0x0000000C //bsAlahuzott | bsAthuzott } TBetuStilus; |
És így használni őket:
| bsHalmaz = bsHalmaz | bsKitevo | bsDolt & ~bsKisatirozott; |
