Ahhoz hogy olyan programokat írhassunk, amelyek csinálnak is valamit, gyakran szükséges az hogy sorba tudjunk rendezni adatokat.
Az adatok rendezése mindig két részből áll:
- El kell dönteni, hogy az általunk felállított sorrendben, a két adat közül melyik van előrébb
- Ha már kettőre el tudjuk dönteni a sorrendet, kell egy algoritmus ami mindet sorba rakja
Íme tehát ezen cikk tartalma:
1, Két adat összehasonlítása
Mivel erről már esett szó az eddigiekben ezért mélységeibe nem mennék bele.
Alapvetően lesz két csoport, a közvetlenül és a közvetetten összehasonlítható adattípus - a közvetleneket egyszerűen lehet összehasonlítani - mivel a gép hardveresen képes erre (processzor logikai egysége) , míg a másikat csak összetettebb algoritmusok által tudjuk elvégezni (bonyolultabb számítást végezve, közvetlenül összehasonlítható értéket állítva elő).
1a, Közvetlenül összehasonlítható adattípusok
Számok összehasonlítása során, függetlenül attól hogy valós/egész a "kacsacsőrökkel" simán ki lehet vitelezni az összehasonlítást:
if (i < j) { ... }
Két karakter esetén szintén ugyanez lesz az eljárás, ha beérjük azzal hogy az adott kódlap karaktertáblája szerinti sorrend alapján fog eldőlni az állítás. Emiatt a már strcmp esetén említett problémák lehetnek - pl. hogy az Á a Z után következik.
A dátum/idő típus defincíójából következően az is összehasonlítható egy egyszerű relációval - hiszen egy későbbi dátumnál 1970 január 1.-je, 0:00 óta több idő telt el, mint egy korábbinál.
1b, Közvetetten összehasonlítható adattípusok
Ha karakterláncokat akarunk összehasonlítani akkor kézzel is írhatunk algoritmust, vagy használhatjuk az strcmp függvényt, illetve ha fontos a természetes betűrendbe rakás, akkor a Windows részét képező "shlwapi.dll" fájlban lévő StrCmpLogicalW függvényt tudjuk használni (PCWSTR = wchar_t*).
Ha tömböket, mátrixokat, stb. akarunk egymáshoz képest sorba tenni, akkor ki kell találnunk azt az algoritmust, amely olyan adatot állít elő, amely már közvetlenül lesz összehasonlítható. Ez számokból álló tömb esetén ez lehet pl. minimum, maximum, összeg, átlag, szórás, norma, stb.
Struktúráknál és unionoknál is ez a teendő, ám ott a mezők alapján kell meghatároznunk egy összehasonlítható értéket.
Az ilyen közvetett összehasonlító megoldásokat érdemes az strcmp-hez hasonló függvénybe, esetleg makróba kiemelni, mivel gyakran lesz rá szükség a rendezés során.
2, A véletlenszámok
A cikk, hogy értelmes legyen - nem előre megadott számhalmazokon - hanem véletlen számokon fogja a rendezési algoritmusokat bemutatni, ezért érdemes erről is egy pár szót ejteni.
Az egyszerű véletlenszám generálás alapja az hogy fogunk egy algoritmust, amely egy adott számból, attól nagyon eltérő számot fog adni.
Ugyanakkor hibátlan megoldás a problémára nincs bizonyos esetekben körkörös lehet a dolog, és a számok már nem is lesznek annyira véletlenek, inkább ismétlődőek.
Ahhoz, hogy minden indításkor más és más számokat kapjunk, szükséges egy kezdőérték megadása - ez lesz az, amivel minden alkalommal más és más számokat fog kidobni az algoritmus.
A csapda ott van a dologban, hogy ennek a kezdőértéknek, indításkor más és más értéket kell felvenni, hiszen azonos kezdőértéknél, azonos véletlenszámokat kapunk.
A kezdőértéket pont ezért szokás az időből származtatni - így kicsi az esélye hogy a program ugyanazokat a számokat adja ki - hiszen a gép az időt nem másodpercben méri, hanem ezredmásodpercben - vagyis hogy két program azonos ezredmásodpercben induljon szinte lehetetlen.
2a, A véletlenszám generálás utasításai
A véletlenszám generálás speciális utasításai, az stdlib.h fájlban találhatóak meg.
Az első lépés, hogy a program indításakor megadjuk a kezdőértéket.
Ezt az srand eljárással tehetjük meg, használata elég egyszerű - egy paramétert kér be, ami a kezdőérték lesz:
srand(12);
Egy ilyen utasítással viszont nem érnénk semmit, az összes példány a programból ugyanazokat a véletlenszámokat dobná ki.
Mint említettük szeretnénk az időt kezdőértéknek megadni, de ehhez kell a time.h fájl is.
time_t ido;
time(ido);
A time utasítás az adott címre/saját visszatérési értékére is kiírja az időt. Ezen dolgokat összerakva:
srand(time(NULL));
Ez már tökéletes inicializálása lesz a véletlenszám generátornak.
A véletlenszám generátor a C-ben a rand utasítás lesz, amely kidob egy véletlen számot 0 és [RAND_MAX = 32767] között (a felső határ lehet nagyobb is).
Általában nekünk nincs szükségünk ilyen számokra, hanem gyakran van inkább pl. 0 és 10 közötti számokra szükség. Ilyen esetekben a maradékképzést használjuk fel:
int i = rand() % 11;
Mivel 11 az osztó, a legkisebb szám ami kijöhet az 0 lesz, a legnagyobb 10 - ha 11 vagy nagyobb lenne a maradék akkor elcsesztük az osztást, szerencsére a gép nem tesz ilyet.
Ha az alsó korlát sem mindegy, mert pl. 1 és 5 közötti számokra van szükség, akkor így változik a megoldás:
int j = rand() % 5 + 1;
A maradékképzés miatt az eredmény 0 és 4 között lesz, amihez ha hozzáadunk egyet, pont a kívánt határokat kapjuk.
Előfordulhat hogy valós számokra van szükségünk, ilyenkor a teendő:
float f = rand() / (float)RAND_MAX;
Ebben az esetben egy 0 és 1 közötti számot fogunk kapni, elég sok tizedesjeggyel.
A típuskonverzió azért kellett hogy valós osztást végezzünk, míg azért van a felső határ hátul mert kisebben a nagyobb, az mindig kisebb, vagy egyenlő mint 1.
Ha már van 0 és 1 közötti valós véletlenszámunk, akkor logikusan előállítható belőle nagyobb is:
-
ha pl 0..10 közötti kell - akkor megszorozzuk 10-zel mindet
-
ha pl. 1..10 között kell - akkor megszorozzuk 9-cel mindet, és hozzájuk adunk 1-et
2b, A véletlenszám generálás általánosítása
- kezdőérték megadása:
srand(<konstans>);
- kezdőérték megadása időből:
srand(time(NULL));
- egész véletlenszám generálás 0..x-ig:
int i = rand() % (x + 1);
- egész véletlenszám generálás a..b-ig:
int j = rand() % (b - a) + a;
-
valós véletlenszám generálása 0..1 között:
float f = rand() / (float)RAND_MAX;
-
valós véletlenszám generálása 0..x között:
float f = (rand() / (float)RAND_MAX) * x;
-
valós véletlenszám generálása a..b között:
float f = (rand() / (float)RAND_MAX) * (b - a) + a;
2c, Példa - egy valós véletlenszámokból álló tömb
| #include
<stdio.h> #include <stdlib.h> #include <time.h> int main() { float f[20]; int i; srand(time(NULL)); for (i = 0; i < 20; i++) { f[i] = (rand() / (float)RAND_MAX) * 9 + 1; printf("%f, ", f[i]); } getchar(); return 0; } |
3, A sorbarakás módjai
Azt állítom, ha már bármely két adatra el tudjuk dönteni hogy melyik áll előrébb, akkor az összesre is.
Ez könnyedén igazolható, hiszen ha kettőre el tudom, akkor másik kettőre is - így pl. háromra megvan - de ha háromra megvan akkor másik háromra is meg lehet, és így tovább...
A probléma csak abban áll, hogy melyiket melyikkel hasonlítsuk össze, úgy hogy a lehető legkevesebb cserével, és összehasonlítással járjon a rendezés.
A példák a továbbiakban n elemű, valós típusú tömbökre fognak vonatkozni.
3a, Rendezés cserével
Egy külső i ciklussal végighaladunk az elemeken (az utolsót kivéve), és az így adott i. elemhez hasonlítjuk egy belső j ciklus által, az összes mögötte lévő elemet. Ha kisebb a j. elem mint az i.-dik, akkor cserélünk, és legközelebb a már kisebb i.-dik elemmel hasonlítjuk össze a többit.
Az algoritmus során, biztosak lehetünk hogy az i. elem előtt álló rész már ki van rendezve - hiszen mindig a legkisebb elem kerül oda (kvázi minimumkeresést végez a belső ciklus). A minimumkeresés optimalizálásával lényegesen gyorsítható az algoritmus, de összetettsége is lényegesen nőni fog.
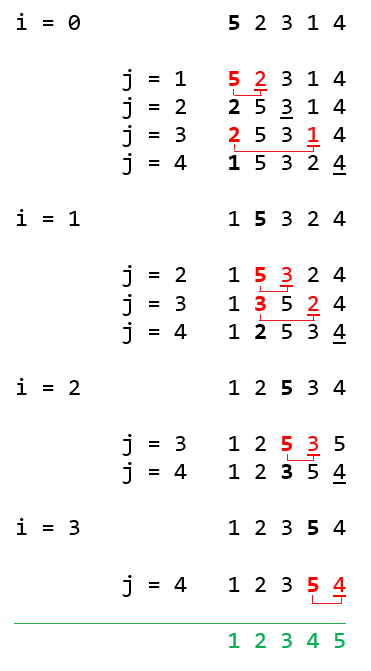
A vastag szám az i által kijelölt elemet takarja, míg az aláhúzott szám a j index által takarja.
Ha a számok pirosak, az azt jelenti, hogy az adott esetben lesz csere, egyébként nem.
Példa:
| #include
<stdio.h> #include <stdlib.h> #include <time.h> #define n 20 int main() { float f[n], p; int i, j; for (srand(time(NULL)), i = 0; i < n; f[i] = (rand() / (float)RAND_MAX) * 9 + 1, i++); for (i = 0; i < n - 1; i++) for (j = i + 1; j < n; j++) if (f[i] > f[j]) { p = f[i]; f[i] = f[j]; f[j] = p; } for (i = 0; i < n; printf("%f, ", f[i]), i++); getchar(); return 0; } |
A példából könnyen készíthető eljárás is:
| void
rendez_csere(float*
f, const
int count) { float p; int i, j; for (i = 0; i < count - 1; i++) for (j = i + 1; j < count; j++) if (f[i] > f[j]) { p = f[i]; f[i] = f[j]; f[j] = p; } } |
Megjegyzés: Az f[i] < f[j] relációra csökkenő sorrendbe fogja rendezni az elemeket növekvő helyett.
Eredmény:
1.502640, 1.667989, 2.409589, 2.668325, 3.351421, 3.824122, 4.032868, 4.186682, 4.299570, 4.923887, 5.049684, 5.581713, 6.849025, 7.722465, 7.917753, 8.172369, 8.344035, 8.848323, 9.266366, 9.612720,
n=10 000 esetén a kigenerálás, és kirendezés együtt 353ms volt, kiíratás nélkül. (i3-6100@4x3,6GHz)
3b, Rendezés közvetlen beszúrással
Minden lépésben [1]-től egyesével n-ig, kiemeljük a csökkenő sorozat szerinti első elemet, és beszúrjuk a megfelelő helyre.
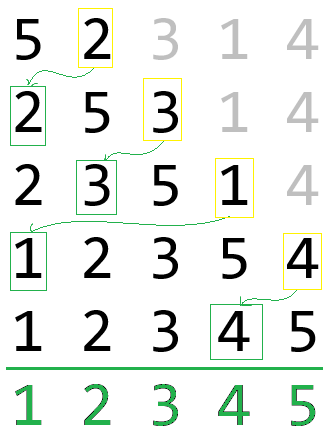
Példa:
| void
rendez_beszur(float*
f, const
int count) { float p; int i, j; for (i = 1; i < count; i++) { p = f[i]; j = i - 1; while (j > 0 && p < f[j]) f[j + 1] = f[j--]; f[j + 1] = p; } } |
Eredmény:
1.309549, 1.509506, 1.761101, 1.904477, 2.037965, 3.424207, 3.677999, 4.876644, 5.563585, 5.704489, 6.121433, 6.522995, 6.755089, 7.203070, 7.675222, 8.158635, 8.161382, 8.186651, 8.759880, 8.945280,
n=10 000 esetén a kigenerálás, és kirendezés együtt 116ms volt, kiíratás nélkül.
3c, Buborék rendezés
Ha a tömböt egy víztartályhoz hasonlítjuk, és a rendezendő tételeknek a buborékok súlyát feleltetjük meg, akkor minden lépés egy buborék felemelkedését eredményezi, a súlyának megfelelő szintre.
Ennél előfordulhat, hogy már nincs szükség cserére, még sem áll le a rendezési művelet. Ez javítható ha jegyezzük hogy történt-e csere a menet alatt, és az első olyannál ahol nem, ott kilépünk az algoritmusból.
Ha esetleg egy folyamatjelzőt (progressbar) is szeretnénk meghajtani, az utolsó csere indexe lehet a k, ahol a k alatti adatok már sorban vannak.
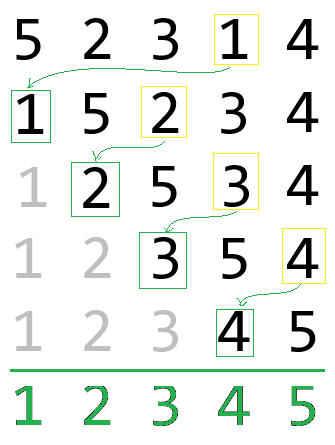
Példa:
| void
rendez_buborek(float*
f, const
int count) { float p; int i, j; for (i = 1; i < count; i++) for (j = count - 1; j >= i; j--) if (f[j - 1] > f[j]) { p = f[j - 1]; f[j - 1] = f[j]; f[j] = p; } } |
Eredmény:
2.166234, 2.609821, 2.839167, 3.663442, 4.012543, 4.224860, 4.413556, 5.248817, 5.681143, 6.104953, 6.107151, 6.149175, 7.120121, 7.287667, 7.811457, 8.197912, 9.398480, 9.602283, 9.644856, 9.803614,
n=10 000 esetén a kigenerálás, és kirendezés együtt 316ms volt, kiíratás nélkül.
3d, Neumann rendezés
Ennek az algoritmusnak akkor lehet előnye ha extrém mennyiségű adatot kell rendezni.
A lényeg hogy felosztjuk a tömböt sok egyforma részre képzeletben, amiket sorba rendezünk (pl ne=2 esetén egyértelmű).
A következő lépések abból állnak hogy ezeket a kisebb részeket összefésüljük, mindig páronként.
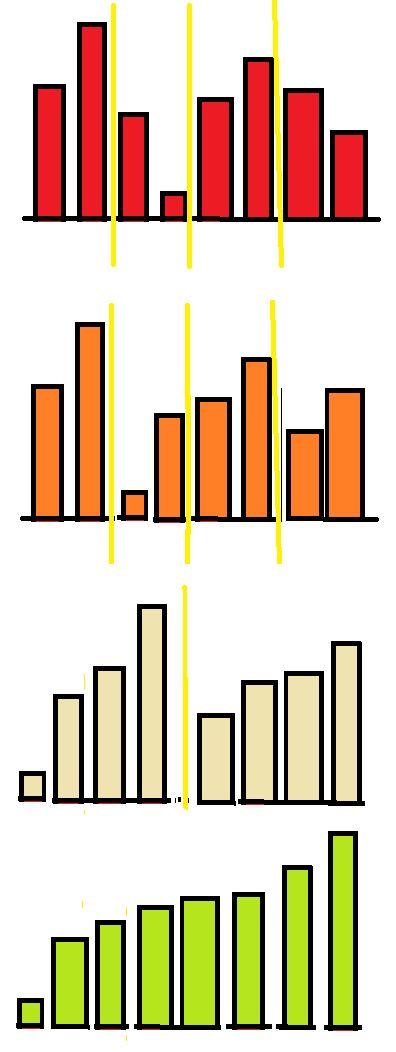
Bizonyos esetekben, kis elemszám esetén lassabb lehet mint a fent leírt algoritmusok, de több millió elemnél már azelőtt végez, mielőtt a többi a negyedéhez érne az adatoknak.
Egy másik előnye, a fentiekkel szemben hogy remekül párhuzamosítató - míg azok egyetlen magon kell hogy fussanak, itt a több processzormag nekiállhat az egyes szeletek összefésülésének, azaz egy időben akár 4-8 részt egyszerre lehet rendezni a tömbben.
4, Szövegek sorba rendezése
Mint erről már korábban szó esett, nagyjából annyi a teendő, hogy a relációs jelet kicseréljük az strcmp-re.
Az egyszerűség kedvéért a cserélős módszer lett átalakítva:
| #include
<stdio.h> #include <string.h> void rendez_csere(char** f, const int count) { char* p; int i, j; for (i = 0; i < count - 1; i++) for (j = i + 1; j < count; j++) if (strcmp(f[i], f[j]) == 1) { p = f[i]; f[i] = f[j]; f[j] = p; } } int main() { char* aszKert[8] = {"malna", "alma", "korte", "barack", "salata", "repa", "szolo", "eper"}; rendez_csere(aszKert, 8); int i; for (i = 0; i < 8; i++) printf("%s, ", aszKert[i]); return 0; } |
Eredmény:
alma, barack, eper, korte, malna, repa, salata, szolo,
Ezen szövegek sorbarakása 52ms időt vett igénybe.
Megjegyzés: Az (strcmp(f[i], f[j]) == 1) sorban, ha (... = -1) alakban módosítjuk, akkor a szövegeket fordított betűrendbe fogja rendezni.
