Mivel a leírás alapvetően C/C++ nyelvhez készül, annak a szintaktikáját követi, ám alkalmazható más programnyelvekhez is.
1, Műveleti sorrend
2, Matematikai alapműveletek
a, Alapműveletek
b, Egyéb alakok
3, Programozási műveletek
a, Inkrementálás/dekrementálás
b, Bevezetés a
logikai műveletekbe
c, Kétoldalú logikai
műveletek
4, Bitenkénti logikai operátorok
5, Mutatók operátorai
6, Egyéb operátorok
1, Műveleti sorrend
Mint a matekban is itt is van műveleti sorrend, de mivel az elején több művelet látható ezért egy kicsit ez komplikáltabb. A legegyszerűbb tudnivalók ha nem akarunk táblázatokat megtanulni:
- Matematikai képleteknél egyszerűen a matematikai műveleti sorrend érvényes, amíg a négy alapműveleten kívül nem keverünk be más dolgokat.
- Ha nem vagyunk biztosak a dolgunkban nyugodtan zárójelezzünk. Az nem rontja el a programot, de biztosak lehetünk hogy azt fogja csinálni amit szeretnénk.
- Ha sok a zárójel szerkesszük Notepad++ segítségével a kódot, mert az kijelzi hogy melyik-melyikhez tartozik.
És íme a híres műveleti sorrend táblázat. Amint látható a zárójel mindent felülbírál, így nyugodtan használhatjuk a sorrend befolyásolására:

2, Matematikai alapműveletek
A C/C++ nyelv matematikai szabályai egyszerűek:
- egész szám és egész szám műveletének az eredménye egész szám lesz
- egész szám és valós szám műveletének az eredménye valós szám lesz
- valós szám és egész szám műveletének az eredménye valós szám lesz
- valós szám és valós szám műveletének az eredménye valós szám lesz
A valós számok bármikor egésszé alakíthatóak (a tizedesek levágásával) az alábbi módon:
| float
f = 3.14; int i = (int)f; |
Illetve visszafele is:
| int
i = 200; float f = (float)i; |
De mi van akkor ha csak egy osztást végzünk el, pl. 3/2? Milyen típusú lesz az eredmény?
A fentebbi szabályok egyértelműen megadják:
| float
f = 3/2;
//az eredmény 1 lesz,
egész/egész=egész float g = 3.0/2.0; //az eredmény 1.5 lesz, valós/valós=valós |
Habár a példa egyértelmű, egyszerűsíthető:
- a fentebbi szabályok szerint elég ha az egyik valós
- az angol írásmódnak megfelelően, ha kint van a tizedespont ("2."), de nincs utána szám az olyan mintha egész érték lenne("2.000..."), de mivel tizedespont van az valós számként lesz tárolva.
Így:
| float
f =
3/2;
//1 float g = 3/2.; //1.5 |
2a, Alapműveletek
Két szám összeadása/kivonása/szorzása ugyanúgy működik mint a valóságban, ugyanakkor az Adattárolás kettes számrendszerben című cikkben leírt korlátok miatt felléphet az ún. túlcsordulás.
Ez úgy működik hogy ha összeadunk két számot és az nagyobb mint a felső határ, akkor a maradékkal körbepörög az alsó határról. Természetesen ez helytelen eredmény, de elkerülhető a típusok helyes megválasztásával, amiknek a korlátai szintén a másik cikkben vannak leírva.
pl.
| unsigned
char i = 200; i = i + 300; /* ez után jogosan várhatnánk hogy az i értéke 500, de mivel az i legfeljebb 255 lehet, az érték 500 - 255 = 245. */ |
| int
i = 32000; i = i + 1000; /* ez után jogosan várhatnánk hogy az i értéke 33000, de mivel az i "-32768" és "32767" között mozog az új érték: -32768 + (33000 - 32767) = -32535. azaz lényegében semmi más nem történt mint körbement a számláló a maradékkal*/ |
A kivonásra ugyanezek a szabályok érvényesek, mindössze azzal a különbséggel hogy itt most a felső határról pörög körbe.
| unsigned
char i = 200; i = i - 300; /* ez után jogosan várhatnánk hogy az i értéke -100, de mivel az i legalább 0 kell legyen, az érték 255 - |200 - 300| = 155. */ |
Az osztás eredménye egész számokra általában nem lesz nagyobb mint a két eredeti szám, itt viszont az alábbi dolgokra kell odafigyelni:
- ha az eredmény egészrészére vagyunk kíváncsiak használjunk
egész típusokat, és számokat
ha az eredményre mint való számra vagyunk kíváncsiak használjunk valós típusokat, és számokat
bővebben: Matematikai alapműveletek - ha az osztás maradékára vagyunk kíváncsiak használjunk egész típusokat, számokat, és a "%" jelet osztásként
Műveleti jelek:
| összeadás | a + b |
| kivonás | a - b |
| szorzás | a * b |
| osztás | a / b |
| maradékképzés | a % b |
2b, Egyéb alakok
Van néhány egyszerűsítő jelölés a programnyelvben, amik a táblázat utolsó előtti sorában láthatóak.
Megértésükhöz talán ez a példa a legegyszerűbb:
| int
i = 10; i = i + 50; /* mi lesz az i értéke? 10 + 50 = 60 */ int j = 10; j += 50; /* az alábbi két sor ugyanaz mint fentebb. egyszerűsített alakban, a második sor jelentése hogy "j = j + 50;" */ /* néhány további példa */ float f = 1.00; //f = 1 f -= 2.00; //f = f - 2; -> f = -1 f *= 3.00; //f = f * 3; -> f = -3 f /= 2.00; //f = f / 2; -> f = -1.5 f = -f; //f = (-1) * f; -> f = 1.5 |
A fenti táblázatban látható egyszerűsített alakok mind használhatóak a programozás során, az érvényességük ugyanaz mint amit a hosszabb alakra érvényesek.
3a, Inkrementálás/dekrementálás
Most már egy változót meg tudunk növelni/csökkenteni eggyel is, a fentiek után - ám a C/C++ erre kiterjesztett lehetőségeink vannak. Ezek a "++" és "--" operátorok, ám elhelyezésük is mélyen befolyásolhat egy-egy műveletet:
| int
i = 200; i = i + 1; /* az i értéke most 201, ez átlátható */ int i = 200; i += 1; /* ez rövidebb */ int i = 200; i++; /* ez még rövidebb, habár itt végig utasításként használtuk az inkrementálást */ |
De mi van akkor ha a növelt értékkel dolgozni is szeretnénk tovább?
| int
j = i++; //j = 201,
lásd lentebb j = ++i; //j = 202, lásd lentebb j = i + 1; //j = 203, lásd lentebb /* itt jön a keverc-kavarc: 1, ha az i után van a ++, a j pont annyi lesz mint az i (201), és ezután növeli meg az i-t csak (i = 202, j = 201). 2, ha az i előtt van a ++, akkor előbb növeli meg az i-t (202), és utána másolja át a j-be (i = 202, j = 202). 3, mivel nem ++ jellel dolgoztunk, a j-be az i-től eggyel nagyobb szám kerül - az i nem változik (i = 202, j = 203). */ /* a j-vel kapcsolatos példa 1. sora helyett kiírható ez is, de az sokkal rövidebb: int j = i; i = i + 1; */ /* a j-vel kapcsolatos példa 2. sora helyett kiírható ez is, de az is sokkal rövidebb: i = i + 1; j = i; */ |
Természetesen ez ugyanúgy értelmezendő az kivonásra is (--).
Bármelyik jelet is használjuk a túlcsordulással továbbra is számolnunk kell.
3b, Bevezetés a logikai műveletekbe
A logikai műveletek során állításokat teszünk fel amit processzor eldönt, és logikai típusként számolhatunk az eredménnyel tovább, vagy később feltételesen hajthatunk végre utasításokat.
Mivel az értékadáshoz használatos műveleti jel már foglalt, ezért a dupla egyenlőség jel lesz az összehasonlítás jele. Ez nagyon gyakori hiba hogy egy feltételes utasításban véletlenül csak egy darab egyenlőség jel kerül - emiatt értékadás történik, és nem összehasonlítás, a program pedig hibázni fog.
| int
i = 200; int j = (i == 200); /* i = 200, j = igaz - vagyis nem nulla */ |
Ha már feltételeket elő tudunk állítani, szükségünk lehet logikai konstansokra, ahogy számításhoz szám konstansokra. Ezek egyszerűek - a logikai típus leírásából adódik hogy "hamis = 0" és "igaz = 1" például. Ugyanakkor ha adott egy logikai típus, eredménnyel mint a felső példában a "j", ne ezekhez hasonlítsuk össze - hanem így használjuk őket:
| if
(j) { /* ha a j igaz */ i = 250; } else { /* ha a j hamis */ i = 150; } |
Mi van akkor ha azt szeretnénk elérni hogy egy állítás az ellentéte legyen? Ha a feltételes utasítást úgy szeretnénk használni hogy akkor működjön az első ág, ha a j-ben lévő feltétel nem teljesül? Íme:
| int
k = !j; /* ellentétes lesz az állítás */ if (!j) i++; /* ha a j-ben lévő feltétel nem teljesül, növelje az i-t */ |
3c, Kétoldalú logikai műveletek
Egy ilyennel már megismerkedtünk, méghozzá ez a "==" jel. Íme egy táblázat ezekről:
| egyenlő | a == b |
| nagyobb, vagy egyenlő | a >= b |
| kisebb, vagy egyenlő | a <= b |
| nagyobb | a > b |
| kisebb | a < b |
| nem egyenlő | a != b |
Talán ezeket nem kell magyarázni, működnek bármilyen egész számon/valós számon/karakteren (ilyenkor a karaktertáblában lévő indexet hasonlítja össze).
Ugyanakkor itt van néhány új művelet:
| vagy | a || b |
| és | a && b |
Ezeket csak simán össze kell olvasni. pl.:
| int
i =
1,
j = 2,
k = 3; if (((i == 1) && (k == 2)) || ((i == 1) && (j != 3))) i++; |
Bár ez elsőre nehéznek tűnik de a feltétel teljesül. Íme lefordítva magyarra:
"ha az (i = 1 és a k = 2) vagy az (i = 1 és a j != 3) akkor növelje eggyel az i-t."
Az állítás első fele bukik mert a k != 2, de a második fele helyt áll - és mivel azt mondtuk vagy az egyik fele, vagy a másik fele ha teljesül akkor csinálja meg az i++; -t.
Mj.: Feltételes utasításban mindig használjunk kettesével ("||", "&&") az és/vagy műveleti jeleit - ha csak egy "|", vagy egy "&" jelről beszélünk akkor bitenkénti logikai operátorról van szó, ami más témakör - és rossz feltételt fog eredményezni.
4, Bitenkénti logikai operátorok
Ezek után nézzük meg hogy a fentebb megismert logikai operátorokat hogyan lehet alkalmazni számokra is. Igen, ezek nem csak logikai típusra, de számokra is alkalmazhatóak amiknek komoly haszna is lehet.
| vagy | a | b |
| és | a & b |
| kizáró vagy | a ^ b |
| alternálás | ~a |
| biteltolás balra | a << b |
| biteltolás jobbra | a >> b |
A számokra való alkalmazáshoz először is kettes számrendszerben kell gondolkoznunk. A számoknak minden egyes bitjén elvégezzük a logikai műveleteket, és megkapjuk az eredményt. Íme néhány példa:
- vagy (ha egyik igaz, az eredmény is az)
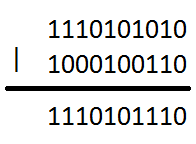
- és (ha mindkettő igaz, az eredmény is az)
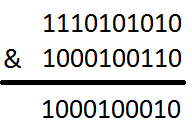
- kizáró vagy (ha egyik igaz, az eredmény is
az - de mindkettő nem lehet igaz)
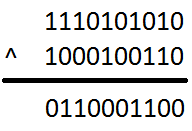
- alternálás (minden állítást megfordít)
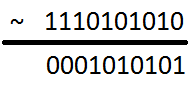
- biteltolás balra (eltolja a biteket egy
megadott mértékkel balra, a kilógó rész le lesz vágva - az új
rész nullákból áll)
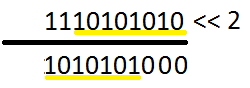
- biteltolás jobbra (eltolja a biteket egy
megadott mértékkel jobbra, a kilógó rész le lesz vágva - az új
rész nullákból áll)
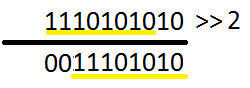
Az hogy ezek a műveletek milyen feladatokra alkalmasak egy külön témakört is megérne - ám megértésük komoly programozási tudást igényel - alapszintű programozáshoz nem fontos ismeretük.
5, Mutatók operátorai
A mutatókkal is lehet műveletet végezni - egyrészt előállítani őket, másrészt pedig elérni a tartalmukat mint változót.
Ha adott egy változó, és szeretnénk a memóriacímét lekérdezni - netán mutatóban tárolni így tehetjük meg:
| int
i =
1; int* p; p = &i; |
Most a "p" az "i" változó memóriacímét tartalmazza.
Ha adott egy mutató és szeretnénk elérni a tartalmát, netán átírni azt akkor azt a "*" operátorral tehetjük meg ha egyoperandusúként használjuk:
| int
j = *p; //j = 1 (*p) = 2; //i = 2 |
A most létrehozott j változó értéke 1 lett, mivel az "i" értékét másolta át bele, mivel oda mutatott a "p". Az első sor tehát ezt jelenti:
"a "j" változó értékét írd át arra az értékre, ami abban a változóban van, aminek a memóriacíme a "p" (ez most az "i")"
A második sor azt mondja hogy:
"annak a változónak a tartalmát, amire a "p" mutat (ez most az "i"), írd át egy kettes számra"
6, Egyéb operátorok
Ami kimaradt a táblázatból:
- [_] - a tömbök indexelését valósítja meg, később kerül elő
- _._ - a struktúrák mezőit érhetjük el vele, később kerül elő
- _->_ - a mutatóban lévő struktúrák mezőihez való, később kerül elő
- sizeof(T) - megadja a T típus/változó méretét byteokban (pl. sizeof(char) == 1)
- (típus)T - a megadott T változót átalakítja a "típus" típusúra. példa: itt
- _,_,_,_,_,... - lista/utasításlista, sok utasítást lehet egy helyén
végrehajtani, a legutolsó értéke lesz az egészé, pl:
int i = 1, j = 2;
int k = (i *= 2, j += ++i, j);
/*
1, i = 2
2, i = 3, j = 5
3, k = 5
ennyi művelet egy sorban - erre való a lista
*/
- _?_:_ - zseb-feltételes utasítás (egyetlen háromoperandusú
operátor) ami a listához hasonlóan menet közben bárhova
beékelhető - első adata a feltétel, második az igaz ág, harmadik
a hamis:
int i = 1, j = 2;
int k = (i > 1 ? --i : j++);
/*
k = ...
első kérdés, az (i > 1)?
ha igen
k = --i: azaz k = 0, i = 0.
ha nem
k = j++: azaz k = 2, j = 3.
feltételes utasítás egy sorban beékelve
*/
A C/C++ egyik legnagyobb dobása a lista és a zseb-feltételes utasítás, mert ezekkel pár sorban is nagyon komplex algoritmusok állíthatóak elő - ám értelmezésük néha már-már fejfájást okozhat mint ez az utolsó két példa ezt megmutatta.
Természetesen lehet pl. hogy a feltétel is egy lista egy ilyen utasításnál és akkor már kész káoszt csináltunk szinte - de ha mi értjük és jól lefut ez végül is nem számít. pl.
k = ((++i, j /= 2, i < j) ? (--i, j *= 2, i - j) : (i *= 2, j++, i + j));
A fenti alapfeltételekből kiindulva:
- Feltétel:
- i = 2
- j = 1
- i < j ? - nem - irány a hamis ág
- Hamis ág
- i = 4
- j = 2
- k = 6
Így lehet kiértékelni egy ilyet a megfelelő adatokkal.
Ezek után már egy abszolútérték utasítás nevetségesen megírható így:
j = i < 0 ? -i : i;
és nincs szükség bonyolult if szerkezetekre.
