Programok
Függvényábrázoló leírása
Ez a program függvények ábrázolását leszi lehetővé tudományos igények nélkül. Lehetőség van az adott függvény deriváltjának illetve második deriváltjának képét is megjeleníteni. Elsősorban függvények elemzésére ajánlom. Be lehet szúrni egy második függvényképet is.
A program az egyszerű használhatóságra törekszik. A legtöbb hagyományos matematikai kifejezést ismeri.
Alapok
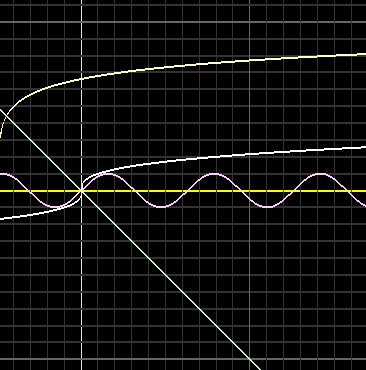
A jobb oldalon a használathoz három beviteli mezőt és (a „Rövid leírás” gombot nem számítva) kilenc gombot találunk. Mindegyiknek határozott föladata van. A bemutatáshoz vegyünk egy mintaföladatot! Tegyük föl, hogy az y = sin(köbgyök(x + 2)) függvényt kell vizsgálnunk; meg kell becsülnünk, hogy a meredeksége hol nagyobb, mint x / 3.
Írjuk hát be a fönti szövegmezőbe, hogy sin(köbgyök(x + 2)), az alsóba pedig, hogy x / 3! Vagyis:
Kattintsunk most a „Függvény kirajzolása” gombra. Ekkor megjelenik az y = sin(köbgyök(x + 2)) függvény képe. Majd kattintsunk a „Derivált függvény” gombra, s ezzel a képhez kék színnel kapcsolódik a derivált függény.
Már csak az y = x / 3 függvényt kell megjelenítenünk. Nyomjuk hát be az alsó „Új függvény berajzolása” gombot, s kész vagyunk. Elvileg a következő kép alakult ki:

A keresett félegyenes kezdőpontjának helye a képről jól becsülhető, amit szükség esetén kinagyíthatunk.
Alapesetben az alapfüggvény képe fekete, a derivált függvényé kék, a második deriválté narancs, a független függvényé pedig zöld. A második deriváltat természetesen a „Második derivált” gombbal jeleníthetjük meg
A „Függvény kirajzolása” gombbal minden esetben csak a legfölső szövegmezőbe írt függvény képe jelenik meg, tehát eltűnnek a deriváltak és a másik függvény.
A rácsot is eltüntethetjük az erre szolgáló gombbal („Négyzetrács kikapcsolása”). Majd újra odakattitva („Négyzetrács bekapcsolása”) ismét megjeleníthetjük.
Nagyítás
Lehetőség van a látott képet nagyítani illetve kicsinyíteni, de csak origóközpontosan. Az erre szolgáló eszközöket az első szövegmező alatt találjuk:

A nagyítás alapesetben 1. A „+” gombbal növelhetjük, illetve a „-” gombbal csökkenthetjük. Ez utóbbi nem csökkenti tovább egy bizonyos értéknél. Az „1” föliratú gombbal azonnal az eredeti 1-es állapothoz térhetünk vissza. A gombok előtti mezőbe tetszőleges értéket is beírhatunk, ami gombnyomásra fog érvényesülni (például ha a „Függvény kirajzolása” gombot használjuk).
Elemfüggvények, műveletek
Mint már ki is derült, a függvények definiálásában általában haszálható magyar megnevezés, mint például a „gyök x”. Ezek a függvények ékezet nélkül is használhatóak, tehát itt írhatunk „gyok x”-et is. Az elemfüggvények után a kifejezés mindig zárójelben áll, például:
„egészérték(x + 2)”,
de ha csak x-re vonatkozik, akkor a zárójel elhagyható, viszont az elemfüggvény neve és az x közé mindenképp (legalább egy darab) szóközt kell tenni.
Egy elemfüggvénynek általában több alternatív elnevezése is van, a „gyök x”-re például:
gyök x – magyar ékezetes alak
gyok x – magyar ékezet nélküli alak
sqrt x – informatikai alak
Az alternatív alakokat néha a számítástechnika és a matematika eltérő jelölései szülik, például a tangensfüggvény esetében:
tg x – matematikai alak
tan x – informatikai alak
A zárójelek értelemszerűen hierarchikusan helyezendők el. Az egyszerű zárójelen kívül speciális jelölésként használható még a { } zárójelpár, mely a törtrészfüggvényt helyettesíti, illetve a [ ], mely az egészértéket. Használható még a |x| kifejezés is, mint x abszolútértéke - és ez csakis egyszerűen x-re alkalmazható (abból kiindulva, hogy a kezdő és záró jel egyformasága miatt természetes hierarchia létrehozása nem lehetséges).
Íme egy összefoglaló táblázat a használható elemfüggvényekről:
| Alak | Leírás | Kiírás |
|---|---|---|
| abs(A) |x| |
az A kifejezés abszolútértéke | |A| |
| arccos(A) acos(A) |
az A kifejezés arkusz-koszinusza | arccos(A) |
| arccsc(A) arccosec(A) |
az A kifejezés arkusz-koszekánsa | arccsc(A) |
| arcctg(A) actg(A) |
az A kifejezés arkusz-kotangense | arcctg(A) |
| arcsec(A) | az A kifejezés arkusz-szekánsa | arcsec(A) |
| arcsin(A) asin(A) |
az A kifejezés arkusz-szinusza | arcsin(A) |
| arctg(A) atg(A) atan(A) |
az A kifejezés arkusz-tangense | arctg(A) |
| atan2(A, B) | az A/B kifejezés arkusz-kotangense | arcctg(A/B) |
| ceil(A) | az A kifejezés fölfelé egészre redukált értéke | -[-A] |
| cos(A) | az A kifejezés koszinusza | cos(A) |
| cosec(A) csc(A) |
az A kifejezés koszekánsa | cosec(A) |
| ctg(A) | az A kifejezés kotangense | ctg(A) |
| egészérték(A) egészrész(A) egeszertek(A) egeszresz(A) floor(A) [A] |
az A kifejezés egészértéke | [A] |
| előjel(A) sgn(A) sign(A) elojel(A) |
az A kifejezés szignuma | sgn(A) |
| exp(A) | az e állandónak az A kifejezés számú hatványa | eA |
| gyök(A) négyzetgyök(A) gyok(A) negyzetgyok(A) sqrt(A) |
az A kifejezés négyzetgyöke |  |
| gyökn(A, B) gyokn(A, B) |
az A kifejezés B kifejezés alapú gyöke |  |
| hatvány(A, B) hatvany(A, B) pow(A, B) |
az A kifejezés B kifejezés számú hatványa | AB |
| köb(A) kob(A) |
az A kifejezés harmadik hatványa | A³ |
| köbgyök(A) kobgyok(A) |
az A kifejezés köbgyöke |  |
| lg(A, B) | az A kifejezés B kifejezés alapú logaritmusa | logBA |
| ln(A) log(A) |
az A kifejezés természetes alapú logaritmusa | logeA |
| max(A1, A2 …) | a fölsorolt kifejezések közül a legnagyobb értékű | S>(Ai)(0) |
| min(A1, A2 …) | a fölsorolt kifejezések közül a legkisebb értékű | S<(Ai)(0) |
| négyzet(A) negyzet(A) |
az A kifejezés négyzete | A² |
| round(A) | az A kifejezés egészre kerekített értéke | ≈A |
| sec(A) | az A kifejezés szekánsa | sec(A) |
| sin(A) | az A kifejezés szinusza | sin(A) |
| tg(A) tan(A) |
az A kifejezés tangense | tg(A) |
| törtrész(A) törtérték(A) tortresz(A) tortertek(A) {A} |
az A kifejezés törtrésze | {A} |
A használható műveleti jelek: +(összeadás), -(kivonás), *(szorzás), /(osztás) és %(osztás maradéka (például 3 % 2 = 1)). A tizedesvesszőt pontnak és vesszőnek is írhatjuk (3,2 = 3.2). Többparaméterű elemfüggvényeknél a számparaméter elé föltétlen tegyünk (legalább egy darab) szóközt, hogy a vessző össze ne tévesztődjön a tizedesvesszővel (például hatvány(2, 3)).
A szorzásjelet nem kell kitenni:
- x elé, ha x előtt szám, zárójeles kifejezés vagy állandó áll
- x után, ha x után zárójeles kifejezés áll
- szám és zárójeles kifejezés közé
- zárójeles kifejezések közé
Egy elemfüggvény zárójeles kifejezésnek számít a szorzásjel bal oldalán (zárójelre végződik és összefüggő).
Néhány példa:
5x + PIx
2(x+2)(x+3)
sin(3x)x
2x(gyök x + 2)
3*Ex(sin x + sin(2x))
(x+2)(x-PI)x
A beírt függvények egymásra hivatkozhatnak a következő módon: az első mezőbe beírt függvényt függvény1 (vagy fuggveny1), a másodikba beírtat függvény2 (a másik programban ehhez jön még a függvény3 és függvény4 ) néven érhetjük el.
Például az első függvényünk ln x + cos x * sin x, és a második sin x * függvény1 + 2. Ekkor ez utóbbi egyenlő sin x * (ln x + cos x * sin x) + 2-vel.
Lefelé is hivatkozhatunk, [például] az elsőből a másodikra [,vagy a másodikból a negyedikre(…), vagy akár láncszerűen vagy többszörösen (például: függvény2 + függvény3 + 2]. A hivatkozott függvényt nem muszáj megjeleníteni, elég ha kattintáskor be van írva a megfelelő mezőbe.), csak a kereszthivatkozást célszerű elkerülni.
Továbbgondolva az előzőeket irányított függvényképeltolás is kivitelezhető. Tekintsük például az y = sin(x + sin(2x)) * x függvényt! Egyszerűen átalakíthatjuk úgy, hogy a függvény2-ben rögzíthessük a jobbraeltolást és a függvény3-ban a fölfeléeltolást:
sin(x-függvény2+sin(2*(x-függvény2)))*(x-függvény2)+függvény3
Ezzel az eltolást paraméteresen adtuk meg, és a paraméterek értékeit a függvény2 és a függvény3 mezőjében számosítjuk.
Az eredeti függvényhez nyilván a függvény2 és a függvény3 mezőjében is 0-nak kell lenni. Ha utána ezeket mondjuk 4-re illetve 5-re módosítjuk, a kép eltolódik 4-gyel jobbra és 5-tel fölfelé.
A szóközök használata tetszőleges (a kötelező szóköz-helyek már említésre kerültek):
(x + 7) (5x + sin x) +5 - (4x)
ugyanazt jelenti, mint:
(x+7)(5x+sin x)+5-(4x)
De voltaképp AKÁRHOVA tehetünk szóközt, ha úgy átláthatóbb a képlet.
Állandók
A legfontosabbnak mondható állandókat ismeri a program:
| Állandó | Írandó |
|---|---|
| π | PI |
| e | E |
| φ | FI |
 |
R2 SQRT2 |
 |
R3 |
 |
SQRT1_2 |
| loge2 | LN2 |
| loge10 | LN10 |
| log2e | LOG2E |
| log10e | LOG10E |
- ahol φ az aranymetszési arányt jelöli (≈1,618).
Használható még a V paraméter is, mely egy gombnyomáskor generálódó véletlenszám 0 és 1 között.
Föltételes utasítás
Gyakran lehet szükségünk föltételes utasításra:
Ha x > 2, akkor y = 5,
ha x ≤ 2, akkor y = 2x
vagy:
Ha {x} = 0, akkor y = sin x,
ha {x} ≠ 0, akkor y = 0
Előszöris fontos: a negáció jele a fölkiáltójel: !, például x > 2 tagadása lehet !(x > 2), de valós számok esetében írhatjuk természetesen a fordítottjával: x <= 2. A <= párja a >=. Az egyenlőséget rövid jelzéssel is lehet tagadni, például: x != sin x, viszont NAGYON FONTOS: föltételben az egyenlőséget DUPLA EGYENLŐSÉGJELLEL (==) kell írni, például: x == 3.
A föltételes utasításra a legegyszerűbb jelhasználat a következő:
(x > 2)? sin x : cos x
mely azt jelenti: ha x kettőnél nagyobb, akkor sin x, egyébként cos x; hasonlóan a (2x > ln x)? x : -x azt jelenti, hogy ha 2x nagyobb, mint ln x, akkor x, máskülönben -x.
Mindezt a gyakorlatba ültetve az előbbi két szöveges meghatározást így írhatjuk:
(x > 2)? 5 : 2x
illetve:
({x} == 0)? sin x : 0
A @ karakterrel megjelölhető, hogy ne legyen értéke a függvénynek, például a
(x != 3)? 5 : @
kifejezés azt jelenti, hogy ha x értéke nem 3, akkor az érték 5, a 3 helyen pedig a függvény nincs értelmezve. A (x != 3)? 5 : @ gyakorlatilag ugyanazt jelenti, mint az 5(x + 3)/(x + 3).
A föltételes utasítást behelyezhetjük bárhová, például:
sin((x+2 > cos x)? 3 : ln x) + gyök((x > 0)? x : gyök x)
Továbbá egymásba fűzvén föltételes utasításokat kettőnél több ágat adhatunk hozzá. Így például a
Ha x < 3, akkor y = 5,
ha 3 ≤ x < 5, akkor y = 4,
ha 5 ≤ x < 7, akkor y = 3,
ha 7 ≤ x, akkor y = 2
megfelelője:
(x<3)? 5 : (x<5)? 4 : (x<7)? 3 : 2
Pár szó a működési elvekről
Az alapfüggvény értékeit egy képpontnyi távolságokban számítja ki. Ez azt a mellékhatást eredményezi, hogy nagy meredekségeknél a függvényvonal elpontozódik (ez a jelenség a második programban kiküszöbölhető, esetleges időigényességért cserébe).
A deriváltfüggvényt igen kis ugrások differenciahányadosaiból állítja össze. A második deriváltat az első derivált deriváltjaként képzi.
Nagyításkor az áttételességnek köszönhetően a pontosság arányosan nő a méretnövekedéssel, így a megjelenítési részletesség nem függ a nagyítás mértékétől.
Kiegészítő funkciók
A programba idővel beleépítettem néhány plusz lehetőséget. A legfontosabb az adatok kijelzése, ha az egeret a rajz fölé visszük:

A fölső rész fölső sorában értelemszerűen az x koordináta értéke látható, míg alatta az y-é. Az alsó részben fölül az adott helyhez tartozó origóvektor hossza, alul pedig e vektor beesési szöge (az x tengely pozitív félegyenesével bezárt kisebbik szög, az adott pont x tengelyhez való helyzetére jellemző előjellel) olvasható.
Ha jobbgombbal vagy duplán a rajzfelületre kattintunk, előjön egy kis menü. Ennek segítségével fölvehetünk a rajzra pontokat. Ha egy pontra rávisszük az egeret, megjelennek az adatai:
Tetszőleges számú pontot rajzolhatunk be, és a megfelelő menüponttal mindet törölhetjük. A pontok egyenként is törölhetők, ha rájuk kattintunk, majd a megjelenő konfirmálóablakban megerősítjük a törlést.
A pontok mellett behelyezhetünk szakaszt is, ekkor a második végpont behelyezése után megjelennek az adatok: fölül a szakasz hossza és a szakasz beesési szöge, alul pedig a két pont koordinátái:

Pont és szakasz behelyezése közben a kurzor megváltozik.
Beállíthatjuk, hogy a függvényértékek megjelenjenek folyamatosan az egérmutató x koordinátájára számítva, rendre a megfelelő függvények (aktuális) színében.
A szögmértékegységet (az egérmutatóhoz kapcsolódó adatokhoz és szakasz adataihoz) a menü "Szögmértékegység" pontjára kattintva módosíthatjuk. A gördülőmenüben láthatók az egységfajták, bármelyiket kiválasztva és a kérdőjelre kattintva olvashatunk egy rövid meghatározást az adott mennyiségről.
A menüben lehet ideiglenesen ki-/bekapcsolni az adatok oldalt való megjelenítését.
A színek megváltoztatásakor előjön az alábbi ablak:
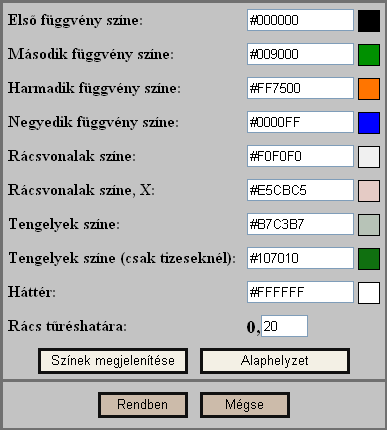
Lényegében értelemszerű a kitöltés. A jobb oldali négyzet jelzi a színt; ha rákattintunk, egy kis paletta jelenik meg segítségként, melyből színt választhatunk. Ha saját kezűleg írunk színkódot, akkor a Színek megjelenítése föliratú gombbal jeleníthetjük meg a színeket a kis négyzetekben. A rács tűréshatára azt jelenti, hogy mekkora nagyítás alatt ne jelenjenek meg az egyes helyiértékek alatti rácsvonalak (csak a tízesek). A Tengelyek színe (csak tizeseknél) ez előbbire vonatkozik: a tengelyek színe akkor, amikor csak a tízes rácsvonalak látszódnak. (Ha a rács tűréshatárát nem állítjuk át és csak a gombokkal irányítjuk a nagyítás mértékét, akkor alapértelmezésben nem kerülünk szembe azzal, hogy eltűnnek az egyes helyiérték rácsvonalai.)
Egy erőteljesen kiszínezett ábra: