Projektmenedzsment


a projektmenedzsment alapjai

hálótervezés

(1) a projekt tevékenységeinek és a tevékenységek logikai kapcsolatainak a meghatározása

a lehetséges kapcsolattípusok:
 
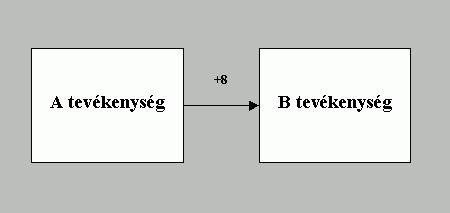
vég-kezdet (FS: Finish-to-Start)
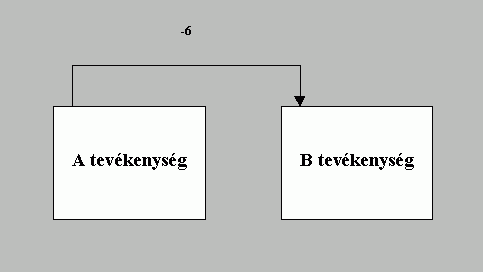
kezdet-kezdet (SS: Start-to-Start)
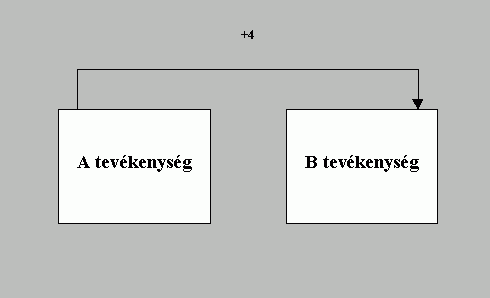
kezdet-vég (SF: Start-to-Finish)
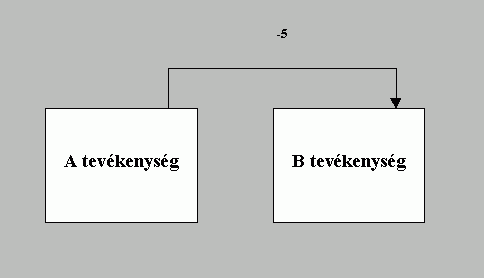
vég-vég (FF: Finish-to-Finish)

PERT diagram készítése (példa: ajándékkönyvtár feldolgozása)

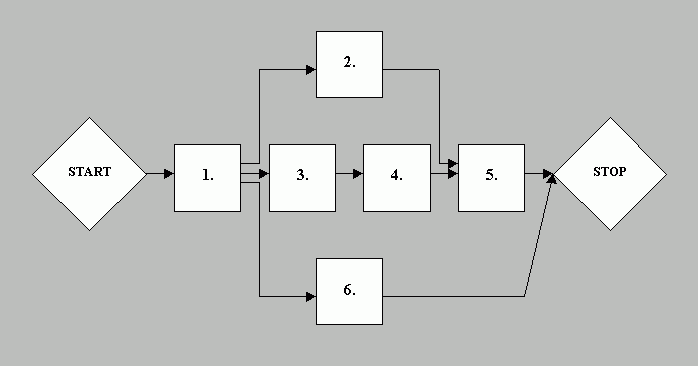
(2) a tevékenységek erõforrás-igényének meghatározása

kiinduló adatok:

a tevékenységek értelmezése és tervezett erõforrás-igénye:
 
tevékenység kódja és megnevezése
tevékenység normája
[db / embernap]
tényleges munkaigény (W)
[embernap]
tervezett dolgozószám (D)
[ember]
várható idõtartam (T)
[nap]
 tervezett munkaigény (W)
[embernap]
1: könyvek válogatása
150
20
4
5
20
2: raktári férõhely felszabadítása
250
8
2
4
8
3: leltározás
100
20
1
20
20
4: könyvek feldolgozása
25
80
3
27
81
5: raktározás
200
10
3
4
12
6: csoportos (egyszerûsített) feldolgozás és a könyvek csoportos elhelyezése a raktárban ("kupacolás")
50
20
1
20
20
összesen:
158
161

Optimális esetben a tervekben pontosan annyi munkát szánunk a tevékenységekre, amennyi a munkaigényük, azaz

W(tényl) = D*T = W(terv)

teljesül. A gyakorlatban azonban ez nem mindig valósítható meg (pl. a 4. és 5. tevékenységek esetén), ezért a tevékenységek tervezett összes munkaigénye (itt: 161) nem mindig egyezik meg a tevékenységek tényleges összes munkaigényével (itt: 158). Mivel azonban egy tevékenység munkaigényét mindig ki kell elégíteni, W(terv)>=W(tényl) minden egyes tevékenységre, és a tevékenységek összes munkaigényére is teljesül.

(3) a háló ütemezése

a tevékenységek ütemezésével kapcsolatos legfontosabb adatok ábrázolása MPM diagramon:

a tevékenységek ütemezése MPM hálón:

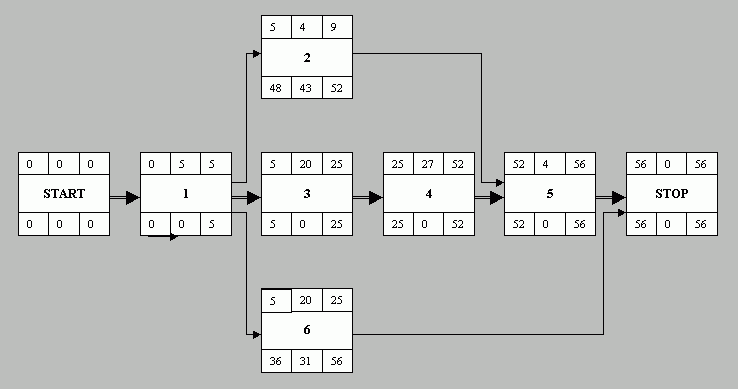
a számítás menete:

A tevékenységek legkorábbi kezdési idejét úgy számítjuk ki, hogy a tevékenység közvetlen elõzményeinek legkorábbi befejezési idejei közül a legnagyobbat vesszük. Például

legkorábbi kezdés(3) = legkorábbi befejezés(1) = 5

legkorábbi kezdés(5) = Max ( legkorábbi befejezés(2),  legkorábbi befejezés(4) ) = Max(9,52) = 52

A tevékenységek legkésõbbi befejezési idejét úgy számítjuk ki, hogy a tevékenység közvetlen következményeinek legkésõbbi kezdési idejei közül a legkisebbet vesszük. Például

legkésõbbi befejezés(4) = legkésõbbi kezdés(5) = 52

legkésõbbi befejezés(1) = Min ( legkésõbbi kezdés(2),  legkésõbbi kezdés(3), legkésõbbi kezdés(6) ) = Min(48,5,36) = 5

A maximális tartalékidõ kiszámítása:

maximális tartalékidõ = legkésõbbi befejezési idõ - legkorábbi kezdési idõ - tevékenység idõtartama

Például:

maximális tartalékidõ(6) = 56 - 5 - 20 = 31

Azokat a tevékenységeket, amelyeknek a maximális tartalékideje zérus, kritikus tevékenységeknek nevezzük. Például az MPM hálón ilyen tevékenységek az 1, 3, 4 és 6 kódszámú tevékenységek. A kritikus tevékenységekre a projekt végrehajtása során különös figyelmet kell fordítani, ugyanis ha a kritikus tevékenységeket nem sikerül a tervezett idõn belül végrehajtani, akkor a projekt végrehajtási ideje az idõtúllépés mértékének megfelelõen megnõ, ami például a tervezett határidõ túllépéséhez vezethet.

Azokat a tevékenységeket, amelyek idõtartama zérus, látszattevékenységeknek nevezzük.

Az MPM hálón azt az utat (vagy élsorozatot), amely a START látszattevékenységbõl a STOP látszattevékenységbe vezet, és csomópontjaiban csak kritikus tevékenységek szerepelnek, kritikus útnak nevezzük. Például az MPM hálón ilyen a

START - 1 - 3 - 4 - 5 - STOP

út, amelyen az éleket dupla nyilakkal jelöltük. Figyeljük meg, hogy a kritikus út hossza (azaz a kritikus úton levõ tevékenységek végrehajtási idejének összege) megegyezik a háló átfutási idejével, azaz azzal a legrövidebb idõtartammal, amely a háló összes tevékenységének végrehajtásához szükséges.

(4) a projekt optimalizálása

A projekt tevékenységeinek ütemezését Gantt diagramon (ún. sávos ütemterven) szemléltethetjük, ha feltételezzük, hogy
    (a) minden tevékenység elkezdõdik a legkorábbi kezdési idõpontban és
    (b) minden tevékenység a tervezett idõ alatt végrehajtódik:

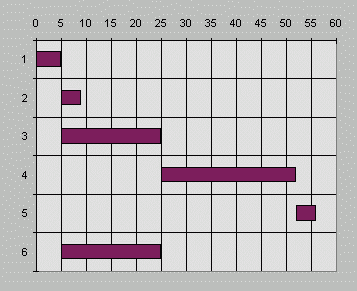
A diagram X tengelyén az idõt, az Y tengelyen pedig a projekt tevékenységeit ábrázoltuk. Például a diagramról leolvasható, hogy a 3-as kódszámú tevékenység (leltározás) az 5. napon kezdõdik és a 25. napon fejezõdik be, ha minden a tervek szerint halad.

A tevékenységek várható emberi erõforrás-igényét leterheltségi diagramon szemléltethetjük:

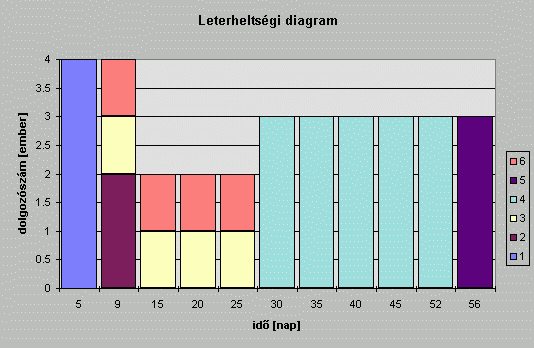
A diagram X tengelyén itt is az idõt ábrázoltuk (napokban), azonban most a tengely skálabeosztását azokhoz a napokhoz igazítottuk, amelyeken valamelyik tevékenység elkezdõdik, ill. befejezõdik. Az Y tengelyen az adott napokon igénybe vett alkalmazottak számát (azaz leterheltségét) ábrázoltuk A diagramból például leolvasható, hogy az 5. és 9. napok között négyen, a 20. és 25. napok között ketten, a 25. és 30. napok között pedig hárman dolgoznak.

A leterheltségi diagram alatti terület a projekt teljes munkaigényét adja meg. Esetünkben

W(terv) = (9-0)*4 + (25-9)*2 + (52-25)*3 + (56-52)*3 = 36 + 32 + 81 + 12 = 161 [embernap]

Mivel a projektben részt vevõ dolgozók száma D(össz) = 4 [ember], és a projekt tervezett idõtartama T(össz) = 56 [nap], elvileg

W(max) = D(össz) * T(össz) = 4*56 = 224 [embernap]

munkát tudnának a dolgozók elvégezni, ha minden napra jutna számukra munka. Tehát a projektterv hatékonysága jelenleg

h = W(terv) / W(max) * 100% = 161 / 224 * 100% = 72%

A szabad kapacitás 224 - 161 = 63 [embernap], ez a projekt 56 napos átfutási idejét figyelembe véve átlagosan

s = (W(max) - W(terv)) / T(össz) = 63 / 56 = 1.125 [ember]

szabad kapacitást jelent naponként.

Attól függõen, hogy a projekt tervezése során milyen elsõdleges projektcélokat tûztünk ki magunk elé, a fenti projekttervet vagy elfogadjuk, vagy nem:

Ha szükség van rá, a projekt optimalizálására a következõ elvi lehetõségek állnak rendelkezésre:

a könyvtári rendszerfejlesztési projekt
Boda István, 2005. március 8.