Számhalmazok

A matematikában mindig figyelnünk kell, hogy milyen környezetben is számolunk, dolgozunk; tehát mi is az alaphalmazunk, melyben értelmezve vannak a feladatok. A számhalmazok a következőek: Természetes számok a pozitív egész számok halmaza és a 0 {0; 1; 2; 3; ...} a 0-t nem minden esetben számolják a természetes számok közé jele: N ebben a halmazban az összeadás és a szorzás végezhető el mindig, a kivonás és az osztás nem minden esetben Egész számok a természetes számok és a negatív egész számok halmaza {...; -3; -2; -1; 0; 1; 2; 3; ...} jele: Z szorozni, összeadni és kivonni lehet mindig a halmaz számait, de osztás esetén kiléphetünk a halmazból Racionális számok azok a számok, melyek felírhatóak (a/b) alakban a; b ∈ Z a; b ≠ 0 jele: Q mind a 4 alapművelet elvégezhető benne úgy, hogy a halmazból nem lépünk ki (+ - × ÷) Irracionális számok nem felírhatóak (a/b) alakban; végtelen, nem szakaszos tizedestörtek pl.: pi; e; √2; √5 jele: Q* Valós számok Q ∪ Q* jele: R

A matematika számelmélet része főként az oszthatósággal foglalkozik, azaz annak felhasználásával kutatja a mélyebb dolgokat. Sok helyütt fontos lehet meghatároznunk, hogy 1-1 számnak mely számok az osztói. Ehhez ad segítséget a következő összefoglalás: Oszthatóságok az egész számok halmazán; egy szám osztható ... 1-el - minden szám osztható 1-el 2-vel, ha az utolsó számjegye páros; 2, 4, 6, 8, 0 3-al, ha a szám számjegyeinek az összege osztható 3-al 4-el, ha a szám 5-re vagy 0-ra végződik 5-el, ha a szám 5-re vagy 0-ra végződik 6-al, ha a szám osztható 2-vel és 3-al is 7-el, ha a számjegyeit hátulról hármasával csoportosítva és váltakozó előjellel összeadva a kapott szám osztható 7-tel 8-al, ha a szám utolsó 3 jegyéből alkotott 3jegyű szám osztható 8-al 9-el, ha a szám számjegyeinek az összege osztható 9-el 10-el, ha a szám 0-ra végződik 11-el, ha a szám páros helyein álló számjegyek összegéből kivonjuk a szám páratlan helyein álló számjegyek összegét, és az így kapott szám osztható 11-el 12-vel, ha osztható 3-al és 4-el is 13-al, erre nincs szabály 14-el, ha osztható 2-vel és 7-el is 15-el, ha osztható 3-al és 5-el is 16-al, ha a szám utolsó 4 jegyéből alkotott 4jegyű szám osztható 16-al 20-al, ha a szám 00, 20, 40, 60 vagy 80 -ra végzódik 25-el, ha az utolsó 2 számjegye 00, 25, 50 vagy 75 50-el, ha az utolsó 2 számjegye 00 vagy 50 100-al, ha az utolsó 2 számjegye 00 125-el, ha a szám utolsó 3 jegyéből alkotott 3jegyű szám osztható 125-el ezek a szabályok tágabb körben is alkalmazhatóak egy új tétel segítségével: ha egy "a" számot felosztunk 2 relatív prím szorzatára, akkor egy akármely "b" szám osztható lesz "a" számmal, ha a "b" szám osztható a kapott relatív prímek mindegyikével általános esetben egy szám osztható "a" számmal, ha osztható "b"-vel és "c"-vel, abban az esetben, ha "a = b*c", és (b;c) = 1 ("b" és "c" relatív prímek)

Számelméleti tételek (a, b, c, n, k ∈ Z): a|a 1|a a|b ⇒ a|(b*c) a|b és b|c ⇒ a|c ⇒ Tranzitív tulajdonság a|b és a|c ⇒ a|(b+c) a|b és a|c ⇒ a|(b-c) a|b és a|(b+c) ⇒ a|c a|b és b|a ⇒ |a| = |b| a|(b+c) és a|b ⇒ a|c a|bn és b|an ⇒ a|(a+b)n (a-b)|(an-bn) (a+b)|(an+bn), ha n = 2k+1 (a+b)|(an-bn), ha n = 2k A számelmélet alaptétele kimondja, hogy minden 1-nél nagyobb természetes szám (sorrendtől eltekintve) egyértelműen felosztható prímszámok szorzatára.

Prímszámok: (~törzsszámok) Azok a természetes számok, melyeknek pontosan két osztójuk van; az 1 és önmaguk (weboldalon 17ezerig felsorolva; itt) (pl.: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...) "A 2 egy páros prímszám, amely tulajdonsággal páratlan a prímszámok körében." Csebisev tétele: bármely nullától és egytől különböző pozitív szám és a kétszerese közt van prímszám hasonló sejtés: bármely 1-nél nagyobb 2 négyzetszám között van prímszám Tétel: Végtelen sok prímszám van. Ezt először Eukleidész írta le "Elemek" című művében. Tegyük fel, hogy a prímszámok darabszáma véges. Legyen ez a szám m. Szorozzuk össze mind az m darab prímet, majd adjunk hozzá egyet. A kapott szám egyik prímmel sem osztható a halmazunkból, hiszen bármelyikkel osztva egyes maradékot kapunk, az egy pedig egyik prímmel sem osztható. A szorzat tehát vagy maga is prím, vagy osztható egy olyan számmal, ami nincs benne a fenti véges halmazban. (Ez azért igaz mindig, mert minden 1-nél nagyobb egésznek van prímosztója.) Mindkét esetben legalább m+1 darab prímszám létezik. A fenti érvelés viszont nem függ m értékétől, így (m + 1)-re is ugyanígy felírható. Így tehát a prímszámok darabszáma nagyobb bármely adott véges számnál. Összetett számok: azok a természetes számok, melyeknek 2-nél több osztójuk van Bővelkedő számok: minden olyan egész, amelyek kisebbek osztóik összegénél (önmagukat nem számítva) (pl.: 212, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, ...) Hiányos számok: minden olyan egész, amelyek nagyobbak osztóik összegénél (önmagukat nem számítva) (pl.: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, 34, 35, 37, ...) Tökéletes számok: azok az egészek, melyek megegyeznek osztóik összegével (önmagukat nem számítva) (pl.: 6, 28, 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128, 2658455991569831744654692615953842176, 191561942608236107294793378084303638130997321548169216, ...) minden tökéletes szám 6-ra vagy 8-ra végződik minden páros tökéletes szám {2n-1 * (2n-1)} alakú Barátságos számok: azok az egészek, amelyekre igaz, hogy az egyik szám önmagánál kisebb osztóinak összege a másik számmal egyenlő, és fordítva (pl.: (220, 284) (1184, 1210) (2620, 2924) (5020, 5564) (6232, 6368) (10744, 10856) (12285, 14595) (17296, 18416) (66928, 66992) (67095, 71145), ...) Boldog számok: Azok a pozitív egész számok, amelyekre igaz, hogy ha a számjegyeinek négyzetösszegét összeadjuk, és ezt a folyamatot addig ismételjük, amíg egyjegyű számot nem kapunk, akkor az eredmény 1 lesz (pl.: 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496, ...) Relatív prímek: azok az egész számok, melyek legnagyobb közös osztója 1 (pl.: (1, 2) (8, 9) (20, 81) ...) Ikerprímek: azok a prímek, melyek különbsége 2-2 (pl.: (3, 5) (29, 31) (1031, 1033) ...) Hármas ikerprímek: azok a prímek, melyek különbsége 2-2-2 (csak a 3, 5, 7 trió) Prímszámhármasok: ha 4 egymást követő páratlan szám közül 3 prím (pl.: (7, 11, 13) ...) Mersenne prímek: azok a prímszámok, melyek felírhatóak 2p-1 alakban; ahol "p" is prím (pl.: 7 = 8 - 1 = 23 - 1; 31 = 32 - 1 = 25 - 1) (pl.: 3; 7; 31; 127; 8191; 131071; 524287; 2147483647; 2305843009213693951; 618970019642690137449562111; 162259276829213363391578010288127; 170141183460469231731687303715884105727; ...) a legnagyobb ismert prím (2008 augusztusában felfedezett) is Mersenne-prím 243112609-1 Dupla Mersenne prímek: azok a prímszámok, melyek felírhatóak 2(2p-1)-1 alakban; ahol "p" is prím (pl.: 7; 127; 2147483647; 170141183460469231731687303715884105727, ...) Csillagprímek: 6n (n-1) + 1 alakú prímek (pl.: 13; 37; 73; 181; 337; 433; 541; 661; 937; 1093; 2053; 2281; 2521; 3037; 3313; 5581; 5953; 6337; 6733; 7561; 7993; 8893; 10333; 10837; 11353; 12421; 12973; 13537; 15913; 18481, ...) Boldog prímek: boldog számok, melyek egyben prímek is (pl.: 7; 13; 19; 23, ...) Félprímek (p*q): olyan számok, melyek felírhatóak 2 prím szorzataként (pl.: 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ...) Csupa 1 prímek: prímek, melyek csak az 1-es számjegyet tartalmazzák (pl.: 11; 1111111111111111111; 11111111111111111111111, ...) Balról csonkolható prímek: olyan prímszámok, amelynek balról elhagyva a kezdő számjegyeit mindig prímet kapunk (pl.: 13; 17; 23; 37; 43; 47; 53; 67; 73; 83; 97; 113; 137; 167; 173; 197; 223; 283; 313; 317; 337; 347; 353; 367; 373; 383; 397; 443; 467; 523; 547; 613; 617; 643; 647; 653; 673; 683, ...) Jobbról csonkolható prímek: olyan prímszámok, amelynek jobbról elhagyva a záró számjegyeit mindig prímet kapunk (pl.: 23; 29; 31; 37; 53; 59; 71; 73; 79; 233; 239; 293; 311; 313; 317; 373; 379; 593; 599; 719; 733; 739; 797; 2333; 2339; 2393; 2399; 2939; 3119; 3137; 3733; 3739; 3793; 3797, ...) Woodall-prímek: n * 2n - 1 alakú prímek (pl.: 7; 23; 383; 32212254719; 2833419889721787128217599; 195845982777569926302400511; 4776913109852041418248056622882488319, ...) Faktoriális prímek: (n! + 1) vagy (n! - 1) alakú prímek (pl.: 2; 3; 5; 7; 23; 719; 5039; 39916801; 479001599; 87178291199; 10888869450418352160768000001; 265252859812191058636308479999999; 263130836933693530167218012159999999; 8683317618811886495518194401279999999, ...) Fibonacci prímek: a Fibonacci sorozatban szereplő prímek (pl.: 2; 3; 5; 13; 89; 233; 1597; 28657; 514229; 433494437; 2971215073; 99194853094755497; 1066340417491710595814572169; 19134702400093278081449423917, ...) Mírpek: olyan prímek, melyek jegyeit visszafele olvasva is prímeket kapunk (pl.: 13; 17; 31; 37; 71; 73; 79; 97; 107; 113; 149; 157; 167; 179; 199; 311; 337; 347; 359; 389; 701; 709; 733; 739; 743; 751; 761; 769; 907; 937; 941; 953; 967; 971; 983; 991, ...) Unokatestvér prímek: olyan prímek, ahol "p" és "p + 4" egyaránt prímek (pl.: (3; 7); (7; 11); (13; 17); (19; 23); (37; 41); (43; 47); (67; 71); (79; 83); (97; 101); (103; 107); (109; 113); (127; 131); (163; 167); (193; 197); (223; 227); (229; 233); (277; 281); ...) Sexy (szexi) prímek: olyan prímek, ahol "p" és "p + 6" egyaránt prímek (az elnevezés a latin sex szóból származik, ami 6-ot jelent) (pl.: (5; 11); (7; 13); (11; 17); (13; 19); (17; 23); (23; 29); (31; 37); (37; 43); (41; 47); (47; 53); (53; 59); (61; 67); (67; 73); (73; 79); (83; 89); (97; 103); (101; 107); (103; 109); (107; 113); (131; 137); (151; 157); (157; 163); (167; 173); (173; 179); (191; 197); ...)

Két egész szám legnagyobb közös osztóját (LNKO) úgy kapjuk meg, hogy a két szám prímtényezős felosztása után minden prímtényezőt a legnagyobb közös hatványon összeszorozzuk. jele: (A;B) Két egész szám legkisebb közös többszörösét (LKKT) úgy kapjuk meg, hogy a két szám prímtényezős felosztása után minden prímtényezőt a legnagyobb hatványán összeszorozzuk. jele: [A;B] Egy pozitív egész szám pozitív egész osztóinak számát úgy kapjuk meg, hogy a prímtényezős felosztás után a hatványkitevők egyel megnövelt értékét összeszorozzuk egymással. Egy pozitív egész szám prímtényezős felbontásával megkapjuk annak kanonikus alakját. Összefüggés LNKO és LKKT között: a * b = (a, b) * [a, b]

I 1 II 2 III 3 IV 4 (A "IIII" jelölést az órákon és kártyákon még használják) V 5 VI 6 VII 7 VIII 8 IX 9 X 10 XI 11 XII 12 XIII 13 XIV 14 XV 15 XVI 16 XVII 17 XVIII 18 XIX 19 XX 20 XXX 30 XL 40 L 50 LX 60 LXX 70 LXXX 80 XC 90 C 100 D 500 M 1000 MCXI 1111 MCMXCVIII 1998 (Használják a következő alakokat is, szabálytalanul: MIIM; IIMM) MCMXCIX 1999 (Használják a következő alakokat is, szabálytalanul: MIM; IMM) MM 2000 MMM 3000 A római számjegyeket "csoportosítva" kell felírni, helyi értékek szerint (egyes, tízes, százas, ...), pl.: 2896 = 2000 + 800 + 90 + 6 = MM + DCCC + XC + VI = MMDCCCXCVI 3221 = 3000 + 200 + 20 + 1 = MMM + CC + XX + I = MMMCCXXI 1902 = 1000 + 900 + 2 = M + CM + II = MCMII 7021 = 7000 + 20 + 1 = MM + XX + I = MMXXI A régi jelölésekkel mindössze 4000-ig lehetett számolni, így bevezettek új jelöléseket: a betűjelek két oldalán lévő függőleges vonal 100×ost jelöl a betűjelek felett lévő vízszintes vonal 1000×est jelöl A reneszánsz időkben a könyvek első oldalán szereplő latin szövegekben, vagy a templomok bejárata felett lévő írásokban, ha összeadjukaz ott szereplő római számjegyeket, akkor a könyv megírásának (vagy templom építésének) évszámát kapjuk.

Háromszög-számok: képzésük: a számsor első elemei: 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, ... Fibonacci számok: a számsor első elemei: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, ... 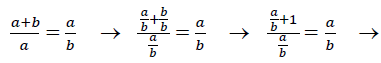a sorozatban három négyzetszám van, a 0, 1 és 144 a sorozatban a négyzetszámokon kívül egyetlen teljes hatvány van, a 8 Fí szám (φ); aranymetszés: Két rész (a és b, a>b) az aranymetszés szerint aránylik egymáshoz, ha az egész (a+b) úgy aránylik a nagyobbik részhez (a), ahogy a nagyobbik rész (a) a kisebbik részhez (b) → 0 = φ2 - φ - 1 → φ1 = 1,618 → φ2 = -0,618 a Fibonacci sorozat egymást követő tagjai hányadosának határértéke a φ szám Euler szám: Pi szám (π) (Ludolph-féle szám): π = 3, 141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 10... egy kör átmérőjének π-szerese a kör kerülete π = egységnyi átmérőjű kör kerülete Graham szám: a gyakorlatban valaha használt lgnagyobb szám az utolsó pár számjegye: ...2464195387 Googol szám: 10100 = googol ≈ 70! a googol nagyobb, mint az ismert univerzum részecskéinek száma, ami becslések szerint 1072 és 1087 közé eshet a Google internetes kereső neve a googol szám tudatosan helytelenül írt változata Googolplex szám: 10googol = googolplex → legnagyobb névvel rendelkező szám Mivel a googolplex szám számjegyeinek száma googol + 1 darab, ezért ezt a számot az univerzumunkban lehetetlen tízes számrendszerben leírni, mivel ha az univerzumunk minden anyagát papírrá és tintává változtatnánk (vagy éppen lemezmeghajtókká vagy számítógépes memóriává), sem lenne elég ahhoz, hogy leírjuk. Pascal-háromyszög: a Pascal-háromszög a binomiális együtthatók háromszög alakban való elrendezése

Műveletek tulajdonságai: Asszociativitás – csoportosíthatóság (x*y)*z = x*(y*z) Kommutativitás - felcserélhetőség a*b = b*a Disztributivitás (a + b)*c = a*c + b*c a*(b + c) = a*b + a*c Tranzitív (~ triviális) A ⊆ B és B ⊆ C ⇒ A ⊆ C Nevezetes azonosságok: (a + b)2 = a2 + 2ab + b2 (a - b)2 = a2 - 2ab + b2 (a + b)*(a - b) = a2 - b2 (a + b)3 = a3 + 3a2b + 3ab2 + b3 (a - b)3 = a3 - 3a2b + 3ab2 - b3 (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc (a + b)*(a2 - ab + b2) = a3 + b3 (a - b)*(a2 + ab + b2) = a3 - b3 Számok összege, szorzata: Számok, számsorozatok összege (summa) Számok, számsorozatok szorzata (produktum)

Egész kitevőjű hatványok:

..........: