Bucka-leképezés ( Bump Mapping)

Ez a tutorial azért készült, hogy a nem teljesen kezdő 3D-s programozóknak bemutassa az egyik legalapvetőbb effektet. Ma már természetesen az effektek többségét vertex és fragment programokkal csinálják, de azért érdemes megismerkedni ezzel a módszerrel is. A tutorialban megpróbálom a hardveresen gyorsított diffúz pixelenkénti megvilágítás technikáját ismertetni. A közismert gyűjtőnév erre a bucka-leképezés (bump mapping). Ez azonban nem határozza meg teljesen, hogy miről is van szó.

Néhány OpenGL kiterjesztés (extension) használatával látványos és gyors buckaleképezést lehet készíteni. Egy ilyen viszonylag egyszerű megvalósításnál azonban némiképp le kell egyszerűsíteni a megvilágítási képletet, hogy a fényforrás felé mutató vektor és a normálvektor skalárszorzatával határozhassuk meg a világosságot pixelenként. A módszer velejárója, hogy nincs spekuláris (specular) világítás, csak egyetlen fényforrást használhatunk, és a fény erőssége nem változik. Azonban sokat nyerünk vele, hiszen nincs szükség valódi fényforrásra, csak egy pozícióra, és a kapott eredmény nagyon látványos tud lenni! A módszer tehát diffúz megvilágítást eredményez, amely azonban nem csak vertexek között interpolált, hanem előre meghatározott értékek alapján történik. Ezzel pedig a részletesség illúzióját lehet kelteni anélkül, hogy hatalmas poligonszámú modelleket kéne használni.

Hogy is fog ez működni?
A működési elve a néző átverése (mint a legtöbb effektnek ). Mivel a valódi megvilágítások is valójában ugyanígy verik át a nézőt, ezért a buckaleképezés semmivel sem rosszabb. A legfőbb része az, hogy a videókártyával egy fekete-fehér árnyalatos textúrát számíttatunk ki a fényforrás helyzetétől és a normálvektorok irányától függően. A fényforrás helyvektorát áttranszformáljuk úgy, hogy az új normálisokkal egy térben legyen (erről később), és a kártya a két vektor skalárszorzatát fogja textúraként használni. A két vektor normalizált, tehát a skalátszorzat képlete alapján (a*b = |a|*|b|*cosy) látható hogy a kiszámolt szín "világossága" csak a bezárt szögtől függ, ami megegyezik a diffúz megvilágítás elvi alapjával. Ezt a textúrát az eddig megszokott textúrával együtt húzzuk rá a vázra, és így a modulálás után a kapott kép olyan, mintha a megvilágítás látszódna rajta. A kulcs itt a modulálás. Ehhez kell, hogy fekete-fehér árnyalatai legyenek csak a textúrán. Ha tehát a világítás erőssége egy pixelen 0, akkor mindegy a textúra színe, mert a végeredmény fekete lesz. A moduláláskor ugyanis a textúrák színeit összeszorozza a kártya textúrázó egysége. A trükk tehát csak abban van, hogy az adatokat olyan formába alakítsuk, hogy a kártya el tudja végezni ezt a műveletet. Na meg persze be kell állítani, hogy ezt elvégezze, de ez az egyszerűbb feladatok közé tartozik. Így tudjuk elérni a nagy sebességet, hiszen a hardveresen támogatott lesz az eljárásunk, és a futás közbeni számítások legnagyobb részét a kártya végzi majd.

Mire is van tehát szükségünk?
Az egyetlen "kellék" a normális térkép (normal map), amely ugyan egy kép, de valójában térbeli vektorokat tartalmaz. Ezt elég egyszerű megérteni, hiszen a színek három komponensből épülnek fel, és a térbeli vektorok is három komponensre bonthatóak. A tárolt vektorok lesznek majd az új normálisok, amelyekkel már pixelenként tudjuk megvilágítani a felületet. A vektorok koordinátáit úgy kell megadni, hogy az x és az y a textúra síkjában lévő két tengely, a z pedig a textúra síkjára merőleges tengely. Az x tengely az s tengellyel párhuzamos (ez a vízszintes textúrakoordináta), az y pedig a t tengellyel. Ha tehát egy teljesen sík felületet szeretnénk, akkor az összes vektornak (0;0;1)-nek kell lennie. így a kép összes pontja (128,128,255)-ös színű lesz. Ezért van az, hogy a normális térképek kékesek, mivel ez a szín is kékes, és a legnagyobb rész általában sík. A példából látszik, hogy a vektort úgy kell színné alakítani (illetve vissza), hogy lehetséges legyen a tengelyeken a negatív érték megadása is. Át lehet konvertálni egy fekete-fehér bucka térképet normális térképpé, de ehhez kell egy arra alkalmas program. Én írtam magamnak egyet, ami egy fekte-fehérből nomrális térképpé alakít egy képet. A két típus között azonban át kell hidalni a köztük lévő kis elvi eltérést. Erről bővebben talán egy későbbi írásban :)...
Példaképpen egy normális térkép:



Hogy lesz a fényforrás pozíciójából olyan vektor, ami felhasználható a számításokhoz?
Na EZ a legnehezebb része az egész módszernek! Ezt így egyben nem is próbálnám meg elmagyarázni, mert valószínűleg nem lenne túl érthető. Ezért inkább most az elméleti hátteret venném, hogy arra később már csak utalni kelljen. Tehát akkor a terek közti transzformációról:
Több teret különböztetünk meg, és ezek között tudjuk transzformálni a vektorokat (így tehát a helyzeteket, és testeket is). Egy teret három egymásra merőleges térbeli egységvektor határoz meg. Ezt nevezzük bázisnak (basis). Ahhoz hogy két bázis között transzformálhassunk egy vektort, ahhoz kell egy olyan transzformációs mátrix amely erre alkalmas. Visszafelé pedig a mátrix inverze kell. Nekünk majd visszafelé kell majd transzformálni, ezért az inverz mátrixokról jegyeznék meg valamit. Ahhoz, hogy tényleg az összes elvégzett transzformáció inverzét kapjuk, az kell, hogy a transzformációk inverzét végezzük el, és fordított sorrendben. Ez a mátrixok szorzásának tulajdonságaiból adódik. Tehát ha mátrixokról beszélünk, akkor fordítva kell a transzformációs mátrixok inverzeit szorozni. Például az én programom a forgatásokat tárolja egy mátrixban. Ezt pedig így valósítja meg:

// Betöltjük az eddigi transzformációkat...
glLoadMatrixf(RotMatrix.GetArray());
// forgatások...
glRotatef(rotX, 1,0,0);
glRotatef(rotY, 0,1,0);
glRotatef(rotZ, 0,0,1);
// Lementjük a transzformációkat... (most már az újakkal együtt)
glGetFloatv(GL_MODELVIEW_MATRIX, Rotmatrix.GetArray());

És eltárolja a forgatások inverzét is:

// Betöltünk egy egységmátrixot...
glLoadIdentity();
// forgatások ellenkező irányban...
glRotatef(-rotX, 1,0,0);
glRotatef(-rotY, 0,1,0);
glRotatef(-rotZ, 0,0,1);
// Megszorozzuk az eddigiekkel...
glMultMatrixf(invRotMatrix.GetArray());
// Lementjük a transzformációkat...
glGetFloatv(GL_MODELVIEW_MATRIX, invRotmatrix.GetArray());

Ebből szerintem látszik miről is van szó. Mivel az első esetben először veszi az eddigi forgatásokat, és csak utána a mostaniakat. Ezzel ellentétben a második esetben (ahol az inverz kell) először végi el a mostani forgatásokat, és csak utánuk az előzőeket. Ezt az elvet alkalmazni kell minden olyan transzformációra, amely nem csak a méretet befolyásolja. Tehát kivételt képez ezalól a mindhárom irányban egyenlő arányú skálázás. Ez ugyanis nem befolyásolja az eredményt.

Először a világ térben (world space) lévő fényforrás helyvektorát kell transzformálni az objektum térbe (object space). Ennek megvalósítása elég egyértelmű, hiszen csak a fent leírt elvet kell követni. Illetve aki szintén mátrixokban akarja eltárolni a transzformációkat, annak pedig már egy példa kódrészlet is volt. Lehetséges lenne inverz mátrixot számolni, de én ennél gyorsabbnak gondolom az eltárolást, hiszen akkor minden kirajzoláskor újra kell számolni az egészet, így azonban csak "frissítjük" a mátrixot.

A következő lépés már kicsit nehezebben érthető. Most ugyanis transzformálnunk kell a vektort az objektum teréből, az érintő térbe (tangent space). Az érintő tér az a tér, amiben a normálisok vannak a textúránkban. Ez a tér az objektum térben egy poligon felszínén van. A bázisa függ a poligon textúrázásától, és a poligon alakjától is. Tehát ha ki akarjuk számítani, akkor szükség van a vertexek pozíciójára, és textúra-koordinátákra. Az érintő tér bázisa az objektum térben, és a textúrában:



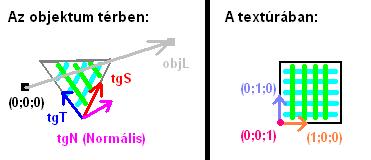
A fenti ábrán mindkét bázis az érintő teret határozza meg. A fenti eset speciális, hiszen a bázis két tengelye is párhuzamos a poligon éleivel. Ez most csak az egyszerűség kedvéért van így. Láthatjuk tehát, hogy a fényforrás helyét meghatározó vektor most objektum térben van. Így azonban nem használhatjuk fel, hiszen nem abban a térben van, mint a normálisok. Ehhez kell az érintő térbe transzformálás. Az érintő teret három kiszámítható vektor határozza meg az objektum terében. Az S érintő (S tangent), a T érintő (T tangent), és a felületi normális, amely a felületből "kifelé mutat", és merőleges arra. Ha ezekből kettő megvan, akkor a harmadik már meghatározható a másik kettő vektoriális szorzataként. Először tehát ki kell számolnunk ezeket. Erre itt az eljárás matematikai leírása:

Vec1 = Vertex3.pos – Vertex2.pos
Vec2 = Vertex1.pos – Vertex2.pos
DeltaS1 = Vertex3.s - Vertex2.s
DeltaS2 = Vertex1.s - Vertex2.s
tgT = |DeltaS2 * Vec1 - DeltaS1 * Vec2|
tgS = |tgT x Vertex.N|

Itt a Vertex1..3.pos a poligon vertexeinek pozíciója, .s az első textúra koordináta, tgT és tgS a T és S érintő vektora, az x a vektoriális szorzat, a .N a normális, a || pedig a normalizáció. A felületi normálist azért vettem itt megadottnak, mivel első sorban játékfejlesztőknek írom a tutorialt. Ebben az esetben pedig valószínűleg valamilyen modellt fognak betölti fájlból, amiben már adott lehet ez a vektor. Ilyen például a 3DS formátum is.
Az érintői teret meghatározó bázisunk tehát már megvan. most már csak transzformálni kéne. Ez már nagyon egyszerű, mivel a három kiszámított vektorból készíthetünk egy transzformációs mátrixot, amivel ezt meg tudjuk tenni. Ez pedig így épül fel:

( tgS.x, tgS.y, tgS.z)
( tgT.x, tgT.y, tgT.z)
( tgN.x, tgN.y, tgN.z)

A tgN a normális. Egy kis csellel azonban nincs is szükség mátrixra, mert az egyébként elvégzendő számításokat három skaláris szorzással is elvégezhetjük. Így valahogy:

tgL.x = tgS . objL
tgL.y = tgT . objL
tgL.z = tgN . objL

Itt a . a skaláris szorzás jele (az angol dot product elnevezésből), az objL a fényforrás vektora objektum térben, a tgL pedig az érintő térben. Ezt minden vertexre el kell végezni minden kirajzoláskor. Szerencsére ezek elég gyors műveletek, tehát a sebességgel nincs gond amíg nem kell magas poligonszámú modelleket kirajzolni. Egyes matematikára érzékenyebb olvasók most talán hiányolják a vektor normalizálását. Igazuk is van, és én is írtam már ennek szükségességéről. Ez azonban már egy új témához vezet...

Van egy olyan módszer, amivel nemcsak normalizálni tudjuk a vektorokat hardveresen, de még meg is oldjuk, hogy szín legyen azonnal, tehát a textúrázó egység számára megfelelő formában tároljuk a vektort. Ez pedig egy normalizációs kocka térkép (normalisation cube map) használata. A kocka térkép úgy általában egy textúra fajta. Ez azonban három dimenziós, és így egy texelt három koordináta határoz meg. Tehát textúra-koordinátáknak megadhatunk egy térbeli vektort. A kocka térkép valójában hat két dimenziós textúra, amiket kocka alakban rendezve kell elképzelnünk. A megadott vektor által "átdöfött" pixel színe lesz a kapott szín. Ezt szemléltetném a következő ábrával:



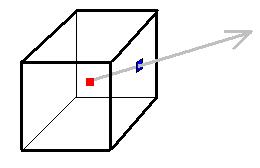
A kocka közepén lévő piros pont az origo jelzése, a kék négyzet pedig a vektor által átdöfött pixel, tehát a kapott szín. Az ábrából látható, hogy a vektornak csak az iránya számít, és nem lényeges a nagysága. Ez teszi lehetővé a normalizálást. Már csak generálnunk kell a program elején egy olyan kocka térképet, amelynek a pontjaiban olyan színek (vektorok) vannak, amelyek az azt átdöfő irányú vektorok normalizált vektorai. Erre egy példa található a mellékelt forráskódban. Ezzel tehát már van normalizált fényforrás vektorunk a a normálisokkal egyező térben. Tehát már csak be kell állítani a textúrázó egységeket hogy kihozzák a várt eredményt. Áttekintésül egy táblázat és egy ábra a céljainkról:





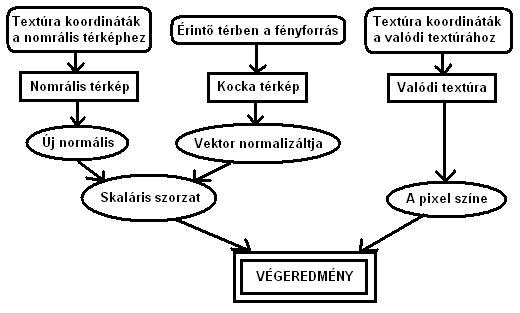
Itt jönnek az OpenGL kiegészítések. Ezekkel bőveben nem foglalkoznék itt. Tudni kell ellenőrizni a támogatottságot, és "lekérdezni" a függvényekhez mutatót, hogy használhassuk azokat. Ez is szerepel a forráskódban. a példában hardveres kirajzolást alkalmazok a grafikus kártya memóriájába másolt vertex és textúra koordináta tömbökkel. Ha ez valakinek új lenne, annak ajánlom a NeHe tutorialt a témában. Az egész alapja a multi-textúrázáshoz is használt módszer, tehát több textúrázó egység használata. Ezeket itt "sorba kell kötni", hogy a megfelelő műveletet végezzék el a megfelelő adatokkal. Ezt a textúrázási környezet (texture environment) beállításával lehet elérni. Ez a környezet azt határozza meg, hogy honnan vegye az adatokat, és hogy milyen műveletet végezzen el velük. Erre egy lehetséges megvalósítás:

Először a nullás egységhez hozzárendeljük a normális térképünket, és megadjuk a textúrázáshoz a koordinátákat. Ezek itt a szokásos textúra koordinátáival egyeznek meg az egyszerűség kedvéért, de lehetséges természetesen erre a célra külön koordinátákat megadni.

glEnable(GL_TEXTURE_2D); // engedélyezzük a 2D-s textúrák használatát
Exts.glClientActiveTextureARB(GL_TEXTURE0_ARB);
Exts.glActiveT extureARB(GL_TEXTURE0_ARB); // aktiválják a nullás egységet
glEnableClientState(GL_TEXTURE_COORD_ARRAY); // engedélyezzük a tömb használatát
glBindTexture(GL_TEXTURE_2D, uiNormalMapID); // hozzárendeljük a normális térképünket
Exts.glBindBufferARB(GL_ARRAY_BUFFER_ARB, uiVBOTexCoords1);
glTexCoordPointer(2, GL_FLOAT, 0, NULL); // megadjuk a koordinátákat

Ezután a kocka térképet rendeljük hozzá az egyes egységhez, és megadjuk textúra-koordinátákként az érintő térben lévő fényforrás irányát mutató még nem normalizált vektorokat...

Exts.glActiveTextureARB(GL_TEXTURE1_ARB);
Exts.glClientAc tiveTextureARB(GL_TEXTURE1_ARB); // aktiváljuk az egyes egységet
glEnable(GL_TEXTURE_CUBE_MAP_ARB); // engedélyezzük a kocka térkép használatát
glBindTexture(GL_TEXTURE_CUBE_MAP_ARB, uiCubeMap); // hozzárendeljük a kocka térképet
glEnableClientState(GL_TEXTURE_COORD_ARRAY); // engedélyezzük a textúra koordináta tömböt
Exts.glBindBufferARB(GL_ARRAY_BUFFER_ARB, 0); // ne a kártya memóriájában lévő tömböt használja
glTexCoordPointer(3, GL_FLOAT, 0, tgLights ); // megadjuk a vektorokat

Most pedig a valódi textúrát rakjuk be...

Exts.glClientActiveTextureARB(GL_TEXTURE2_ARB);
Exts.glActiveText ureARB(GL_TEXTURE2_ARB); // aktiváljuk a kettes egységet
glEnableClientState(GL_TEXTURE_COORD_ARRAY); // engedélyezzük a tömb használatát
glEnable(GL_TEXTURE_2D); // engedélyezzük a 2D-s textúrát
glBindTexture(GL_TEXTURE_2D, uiTexID1); // hozzárendeljük a valódi textúrát
Exts.glBindBufferARB(GL_ARRAY_BUFFER_ARB, uiVBOTexCoords1);
glTexCoordPointer(2, GL_FLOAT, 0, NULL); // megadjuk a koordinátákat

És most következik a környezet beállítása...

// aktiváljuk a nullás egységet...
Exts.glClientActiveTextureARB(GL_TEXTURE0_ARB);
Exts.glActiveT extureARB(GL_TEXTURE0_ARB);

// az egységet beállítjuk, hogy a textúrából vegye a színt...
glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE_ARB);
glTexEnvi(GL_TEXTURE_ENV, GL_SOURCE0_RGB_ARB, GL_TEXTURE);
glTexEnvi(GL_TEXTURE_ENV, GL_COMBINE_RGB_ARB, GL_REPLACE);

// aktiváljuk az egyes egységet...
Exts.glClientActiveTextureARB(GL_TEXTURE1_ARB);
Exts.glActiveT extureARB(GL_TEXTURE1_ARB);

// beállítjuk az egységet, hogy az előző egységtől vegye át az eredményt, és annak vegye a skaláris szorzatát az ő textúrájából vett adattal...
glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE_ARB);
glTexEnvi(GL_TEXTURE_ENV, GL_SOURCE0_RGB_ARB, GL_TEXTURE);
glTexEnvi(GL_TEXTURE_ENV, GL_COMBINE_RGB_ARB, GL_DOT3_RGB_ARB);
glTexEnvi(GL_TEXTURE_ENV, GL_SOURCE1_RGB_ARB, GL_PREVIOUS_ARB);

// aktiváljuk a kettes egységet...
Exts.glClientActiveTextureARB(GL_TEXTURE2_ARB);
Exts.glActiveT extureARB(GL_TEXTURE2_ARB);

// beállítjuk az egységet modulálásra
glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);

A fenti kódrészletben szereplő GL_DOT3_RGB_ARB egy kiegészítés, amely a skaláris szorzat műveletét végezteti el a textúrázó egységgel. Ez a kombináció teszi lehetővé ezt az egész módszert. Ráadásul még gyors is, mivel a GPU végzi a számításokat. A végén található "ARB" arra utal, hogy gyártó-független ez a kiegészítés, tehát megtalálható a mai ATI és NVIDIA kártyákban egyaránt. Célszerű ARB kiegészítéseket használni, mert így nem kell kétszer megírnunk valamit illetve nem lesz márkától függő a programunk.
Még hátra van egy kis rész a kirajzolásból...

Megadjuk a vertexek tömbjét, kirajzoljuk az objektumot, és visszatérünk a normál beállításokhoz...

glEnableClientState(GL_VERTEX_ARRAY); // a vertex tömb engedélyezése
Exts.glBindBufferARB(GL_ARRAY_BUFFER_ARB, uiVBOVertices);
glVertexPointer(3, GL_FLOAT, 0, NULL); // megadjuk a koordinátákat

glDrawArrays(GL_TRIANGLES, 0, uiVertices); // és kirajzoljuk!

glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
Exts.glActiveTextureARB(GL_TEXTURE1_ARB);
glDisable(GL_TEXTURE_CUBE_MAP_ARB);
Exts.glActiveTextureARB(GL_TEXTURE0_ARB);
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
Exts.glClientActiveTextureARB(GL_TEXTURE1_ARB);
Exts.glActiveTextureARB(GL_TEXTURE1_ARB);
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
Exts.glActiveTextureARB(GL_TEXTURE2_ARB);
Exts.glClientActiveTextureARB(GL_TEXTURE2_ARB);
glDisableClientState(GL_TEXTURE_COORD_ARRAY);
glDisable(GL_TEXTURE_2D);
Exts.glClientActiveTextureARB(GL_TEXTURE0_ARB);
Exts.glActiveTextureARB(GL_TEXTURE0_ARB);
glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);