Az algoritmus

Amikor egy problémát meg akarunk oldani, ajánlatos először a konkrét programozási nyelvet félretenni, és azon gondolkodni, milyen lépéseket kell megtenni a probléma megoldásának érdekében. Legjobb, ha egyszerűen leírjuk az instrukciókat. Azon instrukciók halmazát, mely egy feladat megoldásához vezetnek, algoritmusnak nevezzük. Algoritmusokkal a hétköznapokban is lépten-nyomon találkozunk. Instrukciók sokféleképpen megadhatók, például szóban, rajzban, írásban, magyar nyelven, angol nyelven vagy programozási nyelven.
Az algoritmus tehát egy út a felvetődött probléma megoldásához. Legyen a feladat például két darab kréta szerzése. Ahhoz, hogy elvégezzük a feladatot, meg kell terveznünk az elvégzendő tevékenységéket. Lehet, hogy az algoritmus néhány elemi tevékenység egymás után végrehajtandó (szekvenciális) sorozata, mint például:

Menj be a Tanszékre!
Keresd meg az adminisztrátort!
Kérj tőle két darab krétát!
Hozd be a krétát az előadóba!

Lehet, hogy a megoldás bizonyos pontokon nem látható előre és feltételektől függően más és más megoldást kell választanunk. Ilyen például:

Menj be a Tanszékre!
Keresd meg az adminisztrátort!
Ha megtalálod, akkor
Kérj tőle két darab krétát!
különben
Keress máshol krétát!
Gyere vissza az előadóba!

Előfordulhat, hogy egy tevékenységet nem lehet "egyből" végrehajtani, annak végrehajtásához további instrukciók szükségesek. Ilyenkor a tevékenységet részletezni kell. Ilyen lehet például a "Menj be a Tanszékre" instrukció is:

Menj ki az előadóból!
Menj el a C/1 épületbe!
Az 1. emeleten keresd meg a 104. ajtót!
Kopogtass!
Lépj be az ajtón!

Előfordulhat, hogy a megoldás érdekében valamely tevékenységet többször is végre kell hajtani, vagyis ismételni (iterálni) kell. Lehet, hogy az iterációk számát előre tudjuk, lehet, hogy az ismételt végrehajtásnak feltétele van. A "Kérj tőle két darab krétát!" instrukció például két ismétlődő tevékenységből áll:

Csináld kétszer:
Kérj tőle egy darab krétát!

Az iterációt ciklusnak is szokás nevezni. A cikluson a teljes ciklikus folyamatot értjük, az ismétlendő tevékenység pedig a ciklus magja.
Az algoritmus struktúráját tehát szekvenciák, szelekciók illetve iterációk adják, amelyeket tetszőleges mélységben egymásba lehet ágyazni.
A számítógépen megoldandó feladat algoritmizálása esetén nem elegendőek a fenti pongyola megfogalmazások. Az algoritmus leírásának egyértelműnek, pontosnak, lépésenként végrehajthatónak kell lennie. Nem lehetnek előre nem látott akadályok. Számítógép esetén a végrehajtónak, vagyis a processzornak, nincsen ítélőképessége, őt nem lehet bizonytalan helyzetek elé állítani. Mit kell csinálni a "Menj be a Tanszékre" instrukció részletezéseként leírt szekvenciális utasítássor példájában akkor, ha nincs nyitva a Tanszék? Ebben az esetben a "Kérj tőle két darab krétát!" instrukció végrehajthatatlan.
Az algoritmus illetve program leglényegesebb tulajdonságait, és a vele szemben támasztott követelményeket a következő pontokban foglalhatjuk össze:

• Az algoritmus lépésekből (elemi tevékenységekből, utasításokból) áll. Az algoritmus végrehajtása lépésenként történik. Az algoritmus által leírt, és a végrehajtás során megtett lépések sorozatát folyamatnak nevezzük.
• Minden lépésnek egyértelműen végrehajthatónak kell lennie.
• Egy algoritmusban hivatkozhatunk összetett lépésekre is, melynek részletézését később adjuk meg.
• A végrehajtásnak mindig van valamilyen tárgya. Kell valami, amin az utasítást végrehajthatjuk. A "Kérj két darab krétát" instrukció tárgyai a kérő egyén, az adminisztrátor és a kréták. Ezeket a tárgyakat a programozásban adatoknak nevezzük.
• A végrehajtandó instrukciónak mindig valamilyen célja van. A végrehajtás során valamilyen változás következik be  példánkban a kréták az adminisztrátortól átkerülnek az egyénhez.
• Az algoritmusnak vannak bemenő (input) adatai, melyeket felhasznál. A bemenő adatok példánkban az adminisztrátor illetve a kréták. Az algoritmus feladata, hogy a kréták a célhelyre kerüljenek.
• Az algoritmusnak legalább egy kimenő (output) adatot produkálnia kell. Példánkban a kimenő adatok a valahol bemenő kréták.
• Az algoritmus legyen hatékony! Az instrukciók legyenek könnyen követhetők, pontosak, egyszerűek és azokat minél rövidebb idő alatt végre lehessen hajtani!
• Az algoritmust úgy kell megtervezni, hogy az elronthatatlan legyen!
• Az algoritmus olyan legyen, hogy a futó program a felhasználó szempontjait maximálisan vegye figyelembe, azaz legyen felhasználóbarát!

AZ ALGORITMUS TERVEZÉSE

Egy jó algoritmus még a legegyszerűbb program írásánál is komoly segítséget jelenthet. Egy számítógépen megoldandó feladat felvetődése pillanatában máris erős a csábítás, hogy az ember leüljön a számítógép elé, és már gépeljük is az utasításokat. Miután kész vagyunk a beírással, a fordító által jelzett hibákat több-kevesebb idő alatt kijavítjuk. Az ilyen összedobott program azonban a legritkább esetben működik helyesen. És akkor elkezdődik a javítgatás. A program bizonyos adatokkal működik, másokkal nem. Ha valamit kijavítunk, helyette valami másik probléma jön elő. Előbb-utóbb úgy összekeveredünk, hogy már azt sem tudjuk, mi is volt a feladat tulajdonképpen. A toldozás-foltozás nem szerencsés módszer, megbízható programot kizárólag tervszerű programozással készíthetünk!
Az algoritmus megtervezéséhez vezető első lépés a probléma körültekintő elemzése és megfogalmazása. A megoldási módszer keresése csak akkor kezdődhet el, ha a feladatot pontosan ismerjük. Ahhoz, hogy egyértelmű legyen, mi is a feladat, a feladat leírását írásban rögzíteni kell! A feladat leírását feladat specifikációnak is szokás nevezni. Az algoritmust csak a feladat pontos megfogalmazása után próbáljuk elkészíteni, mégpedig programnyelvtől függetlenül.
Az algoritmus tervezésének alapja a részekre bontás. Mivel - elsősorban nagyobb lélegzetű program esetén - a feladatot egyszerre nem tudjuk megoldani, azt kisebb részekre kell bontani. A részeket meg kell oldani, majd a megoldott részeket össze kell állítani. A lebontás illetve összeállítás során a következő kérdések merülnek fel: hogyan bontsuk részekre a nagy feladatot, a részekre bontás után hogy fogjunk hozzá a megoldáshoz, végül hogy történjen az összerakás.
Alapvetően két irányzatot különböztetünk meg:

• A megoldást felülről lefelé fokozatosan, lépésenként finomítjuk és a kis feladatokat csak a végső fázisokban oldjuk meg.
• Először megoldjuk a kisebb feladatokat, és aztán gondolkodunk az összeállítás struktúráján. Ez az alulról felfelé tervezés.

A STRUKTURÁLT ÉS A STRUKTURÁLATLAN PROGRAM

Egy tetszőleges algoritmus a következő elemekből építhető fel:

• Szekvencia: egymás után végrehajtandó tevékenységek sorozata.
• Szelekció: választás megadott tevékenységek közül.
• Iteráció: megadott tevékenységek ismételt, többszöri végrehajtása.
• Feltétel nélküli ugrás: vezérlés átadása a program egy megadott pontjára.

A csak szekvenciákból, szelekciókból és iterációkból építkező programot strukturált programnak nevezzük. A strukturált programozásban a ciklusból való kiugrás fogalma ismeretlen. Ebből következik, hogy a program minden szekvenciájának - és így az egész programnak is - egyetlen belépési és egyetlen kilépési pontja van, ennélfogva a program lényegesen áttekinthetőbb.
Egy bonyolultabb algoritmust nem lehet fejben megtervezni, ahhoz eszközök kellenek. Olyan eszközre van szükség, mely általánosan elfogadott, és mások is ismerik, használják. Az algoritmusok áttekinthető formában való leírására számtalan eszköz létezik. Ilyen a mondatszerű leírás, a folyamatábra, vagy a struktogram. Ezek közül részletesebben a folyamatábrával ismerkedünk meg.

A FOLYAMATÁBRA

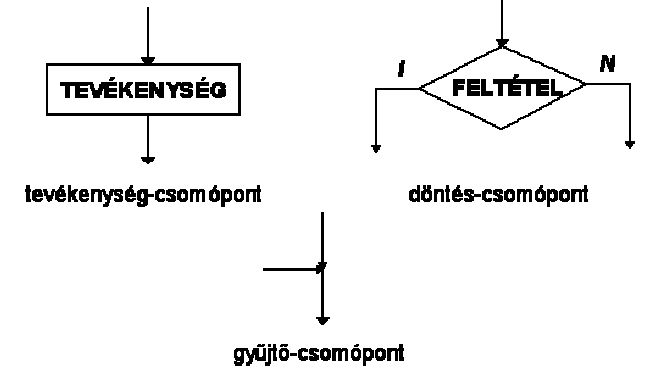
A folyamatábra segítségével a program dinamikus viselkedését, folyamatát részletekbe menően ábrázolni tudjuk. Tekintsük most át a folyamatábra elemi jelöléseit. A program folyását nyilak mutatják, ahol történik valami, ott valamilyen csomópont van. Tevékenységcsomóponton áthaladva a tevékenység végrehajtódik. Döntéscsomóponthoz érkezve a Feltételtől függően a vezérlés az Igaz vagy a Hamis (Igen vagy Nem) ágon folytatódik. A gyűjtőcsomóponton való áthaladás mindig egyértelmű.

Bármely program e három elem segítségével felépíthető, a többi jelölés csak ábrázolási könnyebbség. Kapcsolódási pontot akkor használunk, ha helyhiány miatt ábránkat egy másik lapon folytatjuk. Az adatbevitel és az adatkiírás jelölésére is külön elemeket használunk.

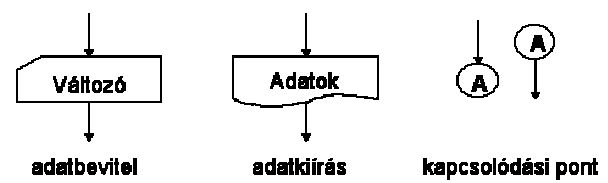
Az iterációkat a következőképpen építjük fel: a vezérlés ismételten visszatér a ciklusmag elé, de az újbóli végrehatás előtt egy döntéscsomópont található, mely megengedi a ciklus elhagyását. Alapvetően két fajta iteráció létezik - az egyik a ciklusmag előtt tesztel, a másik a ciklusmag után, ezek az előltesztelő illetve hátultesztelő ciklusok.

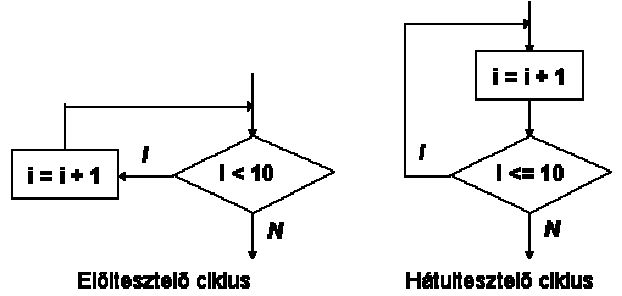
A növekményes ciklus azt jelenti, hogy a ciklusmagban megadott tevékenység előre meghatározott számban, valamely változó (ciklusváltozó) növekvő értékeire hajtódik végre valamettől valameddig. Olyan iterációknál használjuk, amelyeknél pontosan tudjuk a végrehajtások számát. A növekményes ciklust folyamatábrán előltesztelő ciklussal tudjuk megvalósítani úgy, hogy az ábrába beépítjük a ciklusváltozó értékének beállítását, illetve módosításait.
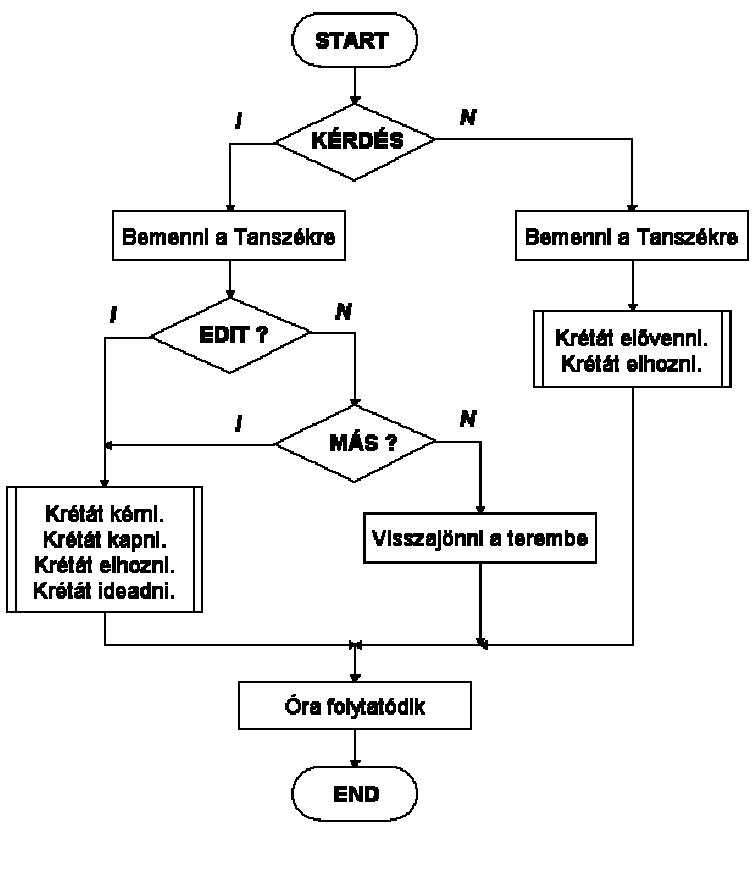
Ezek után nézzük meg, hogy a folyamatábra segítségével hogyan tudjuk leírni a krétás példánkat. Emlékeztetőül a példa: nincs krétám, hozni kellene a Tanszékről.
Részletezve:

1. Megkérdezem, vállalkozik-e valaki arra, hogy bemenjen krétáért a Tanszékre.
2. Ha igen, menjen be a Tsz-re.
3. Kérje meg Editet, adjon egy darab krétát.
4. Ha nincs Edit, keressen valaki mást, s kérjen tőle krétát.
5. Jöjjön vissza a krétával, adja ide.
6. Ha nem talál senkit, jöjjön vissza üres kézzel.
7. Ha nem vállalkozik senki a hallgatók közül, bemegyek én.
8. Kiveszek a szekrényből egy darab krétát.
9. Visszajövök az előadóba, s folytatjuk az órát.

A STRUKTOGRAM

A struktogram egy strukturált ábrázolási módszer, megalkotója Chapin (ezért Chapin chart-nak is hívják). E jelölés annyiban hasonlít a folyamatábrához, hogy a tervezés itt is kívülről befelé történik. Sajnos, ahogy a struktúrában lejjebb megyünk, úgy egyre kevesebb hely marad tevékenységeink leírásához. Példák az alábbi ábrákon láthatók.

A MONDATSZERŰ LEÍRÁS

A mondatszerű leírás lényege, hogy a programot mondatszerű elemekből építjük fel. Annyiban tér el a folyamatos írástól, hogy bizonyos szabályokat be kell tartanunk, a struktúrák képzésére megállapodás szerinti formákat és szavakat használunk. Nézzünk néhány példát:

Be- és kivitel:
Be: ...felsorolás...[megszorítások]
Ki: ...felsorolás...[kiírási formák]

Szekvencia:
Tevékenység1
Tevékenység2
Tevékenység3

Egyágú szelekció:
Ha Feltétel teljesül, akkor Tevékenység(ek) végrehajtásra kerül(nek), egyébként nem. A program az Elágazás vége után folytatódik:
Ha Feltétel akkor
Tevékenység(ek)
Elágazás vége

Kétágú szelekció:
Ha Feltétel teljesül, akkor Tevékenység(ek)1 kerül(nek) végrehajtásra, egyébként Tevékenység(ek)2. Mindkét esetben a program az Elágazás vége után folytatódik:
Ha Feltétel akkor
Tevékenység(ek)1
egyébként
Tevékenység(ek)2
Elágazás vége


Egy szintet vissza, vagy vissza a főmenübe.