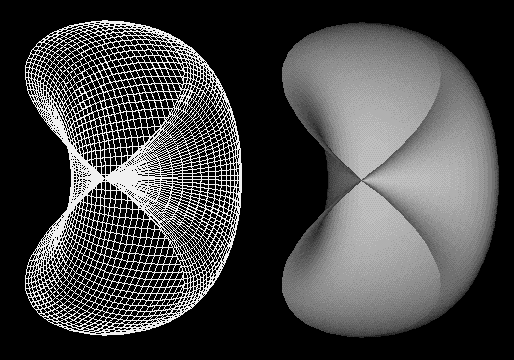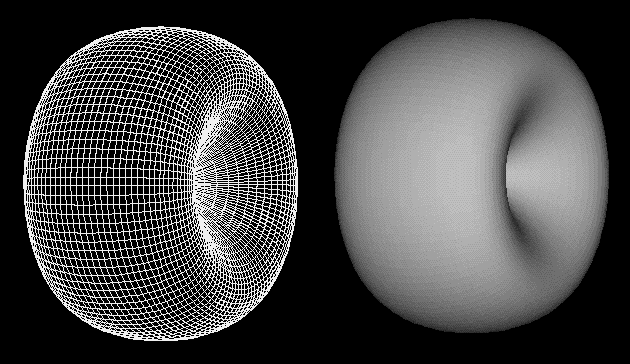

A BINDU, mint felület az egyoldalú,
zárt
és egyszerû felületek osztályába -
E(0,0)-ba
- sorolható, és mint ilyen a PONT
nagyításának
tekinthetõ. Mivel a pont dimenziószámára
nem
csak az igaz, hogy nulla, hanem az is, hogy végtelen,
adódik
az a feltételezés, hogy a BINDU is egy végtelen
dimenziós
felszín. Ugyanakkor az ember természetes módon
arra
asszociál, hogy egy
pont nagyítása gömböt eredményez. Hogyan
lehetne tehát ezt a problémát feloldani, hiszen a
gömb és a bindu egyértelmûen nem egy
topológiai
osztályba tartozik, mivel az elõbbi
kétoldalú,
amíg az utóbbi egyoldalú felszín.
A megoldás igen egyszerû: Ha a gömb
dimenziószáma nem korlátos (végtelen),
akkor
az egyoldalú és így õ is az E(0,0)-ba fog
tartozni.
Az állítás bizonyítása
vázlatosan: N+2 dimenziós gömb N dimenziós
vetületének
van olyan részlete, amelyben a vetített felületi
normális
egy pálya mentén 180 fokot fordul folytonosan. Ehhez az
N+2
dimenziós gömb egy meghatározott
pályáját
kell bejárni. Ilyen pálya biztosan lesz az N+2
dimenziós
felszínen, mivel annak szabadsági foka kettõvel
több,
mint az N dimenziós felszínnek, azaz vannak olyan
pályák
az N+2 dimenziós felszínen, amelyek vetülete egy
pontnak
felel meg az N dimenziós felszínen, miközben a
vetített
felületi normális pl.:180 fokot fordul el. Amennyiben a N+2
dimenziós pályát úgy
módosítjuk,
hogy az az N dimenzióban is egy pályát
eredményezzen
akkor készen is vagyunk: Az N dimenziós gömbben a
vetített
pályán a vetített felületi normális
180
fokot fog fordulni. Ha a kiindulási felszín
dimenziószáma
nem korlátos, akkor minden véges
dimenziószám
esetén a fenti állítás igaz, azaz minden
véges
dimenziószámra a felület egyoldalúnak (is)
látszik
megfelelõ bejárás esetén.
Készült: 2000.02.02.