ANALÓGIÁK
 

   A létfilozófia terén elért kutatási eredmények, illetve a George Kisfaludy által tanított idõfizikai modell több helyen hasonlóságot mutat a modern fizika egyes eredményeivel. Ezen analógiák feltárásának terén elért eredményeimet szeretném megosztani Veletek az alábbiakban.
 

1. IDŐFIZIKAI ÖSSZEFOGLALÓ
 

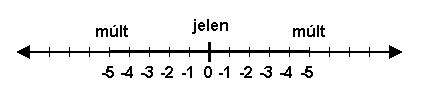
   Az idõfizikai modell a lét euklidészi terében értelmezett, melyben forráspontok és azok terjedõ, táguló múlttere helyezkedik el. Ez a leírás azonos az elõzõ részben tárgyalt létfilozófiai modellel, hiszen a táguló múltszférák a létezõ részhalmazai.

   A múlttér annyi dimenziós, ahány forrásponttal számolunk, hiszen minden egyes jelenhez tartozik egy múlt dimenzió. A forráspontok állandó 'E' tendenciával, koncentrikus kör alakban táguló múltteret hoznak létre. Az 'E' értéke bármely véges pozitív valós szám lehet, amely az idõfizikában célszerûen egységnyi. A múlttér minden egyes egyidejû szférája kör alakú és a keltés pillanatától kezdve, a középpontját megõrizve koncentrikusan tágul. Egyetlen jellemzõje a keltés idõpontja, sugara azonos a keltése óta eltelt idõtartam hosszával. Egy múltszféra azonos a forrásával a keltés idõpontjában, mely azonosságát a tágulása során örökre megõrzi. Ez lehetõvé teszi, hogy egy forráspont megérintse egy másik forráspont múltját.

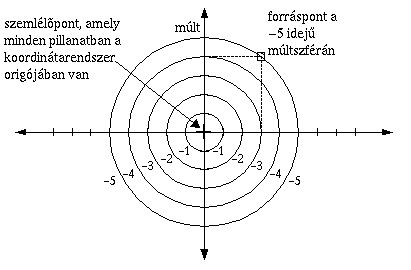
   Az egyes múltterek a forráspontokat mintegy taszítják, külsõ felületükkel tolják. A források egymáshoz képest e taszítás következtében elmozdulnak, így jön létre az RV relatív sebesség. RV megadja a két kiválasztott forráspont közötti idõtartam egységnyi idõ alatt történõ megváltozásának mértékét a szemlélõ sajátidejében, 'E' múlttágulási sebességgel mérve. Az értéke egynél nagyobb is lehet. A múlttér minden egyes pontja RV<1 esetén pontosan egy, RV>1 esetén egy vagy két keltési idõponthoz tartozó múltszférának a része. Az utóbbi lehetõség a forráspontok számának növekedését okozza, ami bõvíti a modell dimenziószámát, ezzel létrehozza a dimenziófejlõdést és lehetõvé teszi a stabil rendszerek ciklikus újrakeletkezését.
   Az anyagi rendszerek a tapasztalataink szerint stabilak. A létfilozófia tükrében szemlélve ez ciklikus belsõ szerkezetet jelent. Az idõfizika szerint a ciklikus belsõ szerkezet RV>1 relatív sebességû forráspontokból kell álljon, de mivel múltterek alkotják, ezért a spirális tere 'E'-vel tágul. A forráspontok önmaguk múltterébe belépve megkettõzõdnek, ezáltal utánpótlást biztosítanak önmaguk fenntartásához. Az anyagi részecskéknek önfenntartó, önbehúzó szerkezetûnek kell lenniük, hiszen egy bizonyos határt nem meghaladó külsõ behatásra szerkezetük jellege megmarad (tehát stabilak). Minden anyagi részecskénél megfigyelhetõ egy határ, ahol a részecske már nem képes kompenzálni a külsõ behatást és szerkezete szétbomlik.
 

2. NEWTON HATÁS-ELLENHATÁS TÖRVÉNYE ÉS A LENZ TÖRVÉNY AZ IDŐFIZIKA TÜKRÉBEN
 

   Külsõ behatásra egy részecske belsõ szerkezete úgy változik meg, hogy stabilitását megõrizze. Ez a szerkezetváltozás megváltoztatja a részecske hullámterét, melynek a környezetére kifejtett hatását erõtérként tapasztaljuk. Ehhez az elvhez leginkább az elektromágnességtanban szereplõ Lenz törvény hasonlítható, miszerint egy tekercsben a fluxus változásának hatására a tekercs olyan önindukciós feszültséget hoz létre, hogy az általa keltett áram kompenzálja a fluxusváltozást. Hasonló törvény Newton II. törvénye, a hatás-ellenhatás elve, amely kimondja, hogy ha egy testre F erõvel hatunk, akkor az a=F/m az erõ irányába mutató gyorsulással fogja megváltoztatni a mozgásállapotát, miközben -F erõvel hat a gyorsító erõ ellen. Az 'm' a test tömege, amely feltételezéseim szerint arányos a testben fellelhetõ ciklikus létrendszerek összes forráspontjainak számával.
 

3. KAPCSOLAT A LORENTZ TRANSZFORMÁCIÓ ÉS AZ IDŐFIZIKAI MODELL KÖZÖTT
 

   A modern fizika, azon belül a relativitáselmélet részét képezõ Lorentz transzformáció képletei a jelenlegi mérési eredmények alapján minden inerciarendszerben érvényesek. De mi is az inerciarendszer a valóságban? Inerciarendszernek a gyakorlatban azt az anyagi struktúrát, mérõeszközt nevezzük, melynek belsõ mozgásainak és torzulásainak sebessége elhanyagolható mértékû a teljes rendszer -számunkra lényeges- relatív sebességéhez képest. Sajnos ez az egyszerû kép ma már az atom felépítése, az elektronok jelentõs sebessége miatt tarthatatlan.
   A ciklikus szerkezet által keltett spirálgömb alakú térben a sûrûséghullámok hullámhossza kisebb kell legyen az általa alkotott részecske átmérõjének Pi-szeresénél, ezért egy anyagi részecske a relativitáselmélet szemszögébõl, makro szinten igen jól modellezhetõ egyetlen forrásponttal. Azonban több részecske által alkotott rendszer, például egy atom már nem modellezhetõ ezen a módon.
   A gyakorlati tapasztalatok szerint a fizikai rendszerek vizsgálata leegyszerûsíthetõ részecskepárok vizsgálatára. Minden összetett, kettõnél több részecskét tartalmazó rendszer leírható az õt alkotó részecskepárok között értelmezett hatások összegeként. Természetesen ez nem jelenti kettõnél több részecske pontos idõbeli leírását, hiszen egyes speciális esetektõl eltekintve a rendszer mûködése már kaotikus kettõnél több résztvevõ esetén. Számunkra ez annyit jelent, hogy a relativisztikus jelenségek vizsgálatához elegendõ két elemi részecskét, mint rendszert tanulmányoznunk. Mivel jelen esetben minden elemi részecskét egyetlen forrásponttal modellezünk, ezért kétdimenziós idõfizikai modellt használunk.
   A vízszintes t tengely a minden pillanatban az origóban tartózkodó, szemlélõpontként használt forrás sajátideje. A függõleges t' tengely a szemlélõponthoz képest RV relatív sebességgel pozitív irányban mozgó forráspont sajátideje. A Lorentz transzformáció képletei a két forráspont szemszögébõl, mint inerciarendszerben értelmezett tömeg, távolság, helyzet és idõpont értékek között teremt matematikai kapcsolatot.
   Szemléltetõ ábra a Lorentz transzformációhoz:

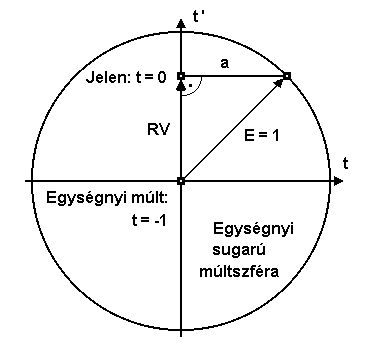
E=1 expand, a létterjedés tendenciája
RV= relatív sebesség, ahol 0<RV<1
a=relatív idõsûrûség
a2+RV2=E2 (derékszögû háromszögnél)
a2=E2-RV2
a=Ö(E2-RV2)
RV=v/c ha E@fénysebesség
x=c*t mert távolság=idõtartam

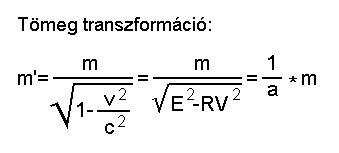
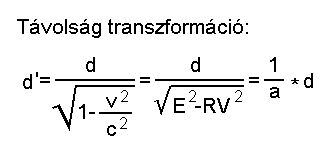
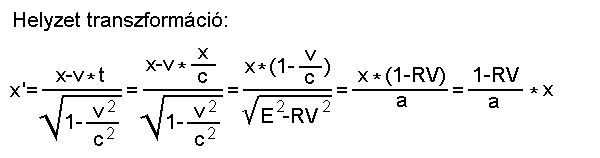
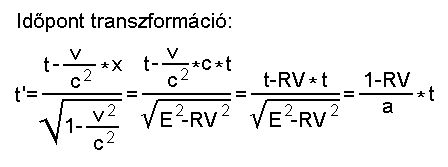
   A fenti egyszerûsítések alapján látható, hogy a Lorentz transzformáció visszavezethetõ a szemlélõ forráspont által érzékelt, relatív mozgó forráspont által kibocsátott múlttér sûrûségére, a forráspontok relatív sebességének függvényében.
 

4. MEMÓRIACELLÁK, A STABILITÁS MAKRO SZINTŰ ALKALMAZÁSÁNAK SZEMLÉLTETÉSE
 

   A stabilitást az idõfizikában egy létezõ forrásrendszer önmagába való visszacsatolásaként azonosítjuk. Hasonló szerkezetek gyakran fellelhetõk a mûszaki életben, egyes gyakorlati megoldásokban. Gondoljunk csak arra, amikor a víz hõmérsékletét a bojler hõszabályzójával stabilizáljuk. Hogyan is mûködik a hõszabályzó? Információs visszacsatolást teremt a vízbe merített hõérzékelõ és a fûtõszál között. Vagyis visszacsatolást, egyfajta közvetett létciklust hoz létre. Könnyen belátható, hogy ilyen visszacsatolás, ún. szabályzási kör nélkül a víz hõmérsékletének közel egyenletes értéken tartása nem valósítható meg.
   A számítástechnika területén szintén találhatunk szemléletes példákat a stabilitás visszacsatolással történõ biztosítására. Legkézenfekvõbb példa erre a memóriacellákban alkalmazott megoldás, ahol a stabilitást biztosító ciklust egy bit információ tárolására használják.:

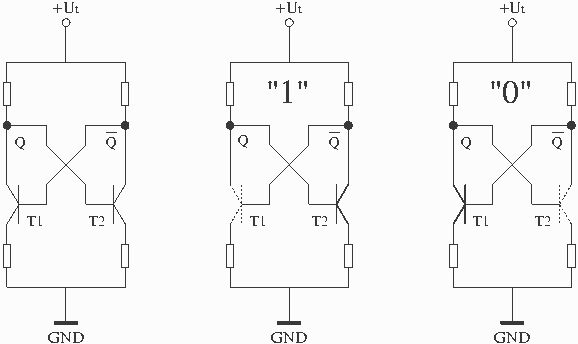
1. Statikus memóriacella szerkezete.
2. Egy értékû bit tárolása, T1 nyitott, T2 zárt.
3. Nulla értékû bit tárolása, T1 zárt, T2 nyitott.

   Egy sztatikus memóriacella egy bit tárolására képes. Lehetséges értékei 0 és 1, melyeket T1 és T2 tranzisztorok nyitott és zárt állapotával tárol a cella.
- 0 értékû bit tárolása esetén T1 zárt állapotú, amelynek hatására T2 bázisának feszültsége magas lesz, melytõl T2 nyitott állapotba kerül. T2 nyitott állapota T1 bázisát alacsony feszültségre kényszeríti, ezzel zárva a kört és állandósítva az állapotot. Nullát T1 átmeneti földelésével lehet beírni a cellába.
- 1 értékû bit tárolása esetén T2 zárt állapotú, amelynek hatására T1 bázisának feszültsége magas lesz, melytõl T1 nyitott állapotba kerül. T1 nyitott állapota T2 bázisát alacsony feszültségre kényszeríti, ezzel zárva a kört és állandósítva az állapotot. Egyet T2 átmeneti földelésével lehet beírni a cellába.
 

5. GYORSAN FORGÓ TESTEK KÖRNYEZETÉBEN TAPASZTALT ANOMÁLIÁK
 

   A forgó testek, mint minden anyagi rendszer stabil anyagi részekbõl tevõdik össze. Az anyag részecskéi a fentiek alapján ciklikus létrendszereket tartalmaznak, melyek eleve forgáshoz hasonlatos mozgást végeznek. Amennyiben ezt az igen nagy sebességû forgást -amely a kölcsönhatások kialakulásáért felelõs- kiegészítjük a test forgatásával, azzal értelemszerûen megváltoztatjuk a test eredõ hullámterét. A test forgása állandó gyorsulásra készteti az azt felépítõ anyagot, amely stabilitásának megõrzése érdekében úgy módosítja hullámterének szimmetriáját, hogy az ellensúlyozza a centrifugális erõt.
   Ez a változás aszimmetrikussá teszi a hullámteret, hiszen a fenti feltételek teljesítéséhez sugárirányban más sûrûségû kell legyen, mint a forgástengely irányában. A múlttér sûrûségének eltérése számtalan "egzotikus" jelenséghez vezet, mint például az órák járásának megváltozása, amely e változás közvetlen következménye. Ezen változások földi mértékben jelentéktelenek és alig mérhetõek, azonban például egy neutroncsillag esetében igen jelentõsek is lehetnek. Ez okozhatja például a neutroncsillag környezetében lévõ anyag akkréciós korongba tömörülését, mielõtt a felszínbe ütközne. Ugyanez a jelenség okozhatja a bolygók pályasíkjának közel egy síkba történõ beállását és lehetséges, hogy hasonló okok felelõsek a galaxisok jól ismert lapos korong alakjáért is.

Készült: 2000. 07.14.

Vissza a tartalomhoz

Következõ írás

(Az univerzum téridõ áramlási rendszerének modellje című képet átugorja a link!)