KEZDETI MEGNYILVÁNULÁSOK
 

1. KÉT FORRÁS KÖLCSÖNHATÁSA

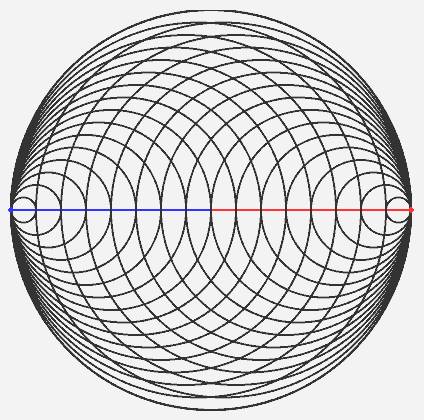
Egy időforrás (legyen: 'A') mindaddig megnyilvánulatlan, amig a létezése egyetlen más időforrás számára sem realizálódik. Ebből a szempontból nézve nincs jelentősége annak, hogy ez a forrás áraszt-e magából gömbszerű időhullámokat, eseményhorizontokat vagy sem, mivel ezekről senki sincs, aki tudomást szerezhetne (1. ábra). Még maga a forrás sem, hisz nem találkozik a saját múlthullámaival. Egy magányos forrás épp ezért nem tud önmagáról, nincs számára idő (ezt jelöljük t0-val), változás, információ, nem végez önfelismerést és nem mozog. A megnyilvánulatlan okforrás (Bindu) tehát gyakorlatilag még nem tekinthető létezőnek, csak vanásnak. Mert létezni annyit jelent: valaki más számára létezni. Épp ezért helyesebb volna a megnyilvánulatlan forrás időhullámait vanási hullámoknak nevezni, megkülönböztetésül a megnyilvánult forrás létezési hullámaitól.
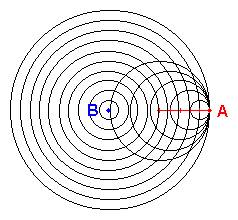
Az idő abban a pillanatban születik meg (ez lesz a t1), amikor egy másik ('B') forrás realizálódik 'A' számára. Az időfizikai világmodellben megfogalmazva: 'B' időhullámai elérik 'A'-t és sugárirányban sodorni kezdik maguk előtt, egységnyi (E=1) sebességgel (2. ábra). De mi történik ekkor valójában? Mindaddig, amig a források közti kölcsönhatásokat kívülről szemléljük, sok érdekesség rejtve marad előttünk. Ahhoz, hogy a teremtés kezdeti pillanatait pontosan megérthessük, bele kell gondolatban helyezkednünk az egyes időpontokba és az alábbi alapvető kérdéseket kell feltennünk magunknak.: Mit látok? Mi történik? Miért van mindez? Lássunk neki a feladatnak!

A szerző megjegyzése: Az itt leírtak szorosan kapcsolódnak az Eseményhorizont következő írásaiban kifejtett témákhoz: Kezdetben vala a létezés, Az idő szerkezete, A pontról, A létezés alapjai, A megnyilvánulás folyamata, Az őskáosz, Teremtési tartományok.
Az 'A' pont szemszögéből nézve abban a pillanatban, amikor őt eléri 'B' legelső kibocsátott múlthulláma, felvillan egy pont a teljesen üres, korom feketeségként leírható, teretlen és időtlen, meghatározhatatlan semmiben. Ez a pont semekkora (nulla) távolságban jelenik meg 'A'-tól, mivel két semekkora pont távolsága a semmiben csakis zéró lehet a két pont számára. Egy harmadik szemlélő számára ugyan úgy tűnhetne, hogy a két pont valahány eseményhorizont rétegnyi (nem térbeli, hanem időbeli!) távolságra létezik egymástól, de itt még nincs harmadik, aki bármit is "láthatna".
Mivel 'B' nulla távolságra fog látszódni 'A'-tól, nincs értelme az iránynak sem, hogy 'A'-tól merre jelenik meg 'B' képe. Ennélfogva 'A' számára 'B' ugyanott fog realizálódni, létezni, mint ő maga, tehát mintha egyek lennének, egy létező pont. A különbség csak annyi, hogy 'A' számára eddig nem létezett 'A', mivel megnyilvánulatlan volt. 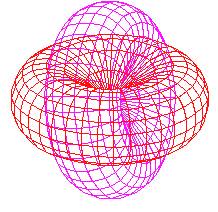Most viszont, hogy 'B' létezni kezd neki, őt önmagával fogja azonosítani, vagyis 'B'-ben felismeri önmagát. 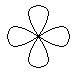Ezt ábrázoljuk a Bindu felhasadásaként, amikor két jelenpont egymást "benyeli" és egymás számára létezni kezd, kiárasztva a létezés eseményének hullámait a végtelenbe (3. ábra). A misztikában ezt szimbolizálja a fénymagnak is nevezett, termőtáj nélküli négyszirmú "virág" (4. ábra).

Mivel 'A' korábban nem létezett még önmaga számára sem, ezért 'B'-t mindenképpen önmagával fogja azonosítani, mivel önmagáról semmilyen és semennyi információja nem lévén, nem végezhet összehasonlítást és nem különböztetheti meg magától a másik originális létezőt. 'B' számára, amikor 'A' legelső hulláma eléri őt, természetesen ugyanez történik. Mivel egyikük sem látja, észleli a másik eseményhorizontjainak gömbszerű tulajdonságát, hisz abból csak egy pontot lát, ami megérinti őt, a kettejük közt kialakuló kölcsönhatás szálszerű lesz. Ugyanígy annak sincs (még) jelentősége, hogy hány időhullám rétegtávolságra vannak a jelenek egymástól az első realizáció szent pillanatában.
Térjünk vissza oda, hogy 'B' legelső eseményhorizontja azonnal tolni, sodorni kezdi maga előtt 'A'-t. 'A', aki eddig gyakorlatilag állt önmagához (és 'B'-hez) képest, most egyből RV=1 sebességgel kezd el mozogni, gyorsulás és tehetetlenség nélkül (mivel itt nincs anyag, energia, csak transzcendens, nulla dimenziós pontok). 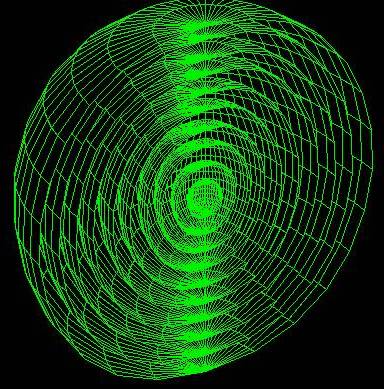Az ő számára ez azzal fog járni, hogy az első realizáció pillanatától kezdve kibocsátott saját időhullámaival megegyező (E=1) sebességgel fog mozogni. Így viszont 'A' számára folyamatosan realizálódik az összes múlthulláma a maga előtt tolt orrkupakban, vagyis önmagát, aki valójában ő és 'B' együtt, egy pontban, szálként fogja észlelni, látni (5. ábra). Tehát 'A' azt látja, hogy ő egy világító, "fehér" szál a "fekete" semmiben, ami folyamatosan nyúlik a végtelenségig.

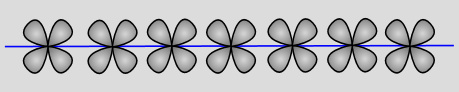
Ez a szál olyan pontok folytonos lánca, amik formailag ugyan azonosak (két Bindu egymásban), de időbeliségükben különbözők. Konkrétan megfogalmazva: a szálban 'A' számára 'B' mindig csak egy pillanatában, a legelsőben látszik, hiszen ő az ahhoz tartozó eseményhorizont rétegen "ül" rajta folyamatosan, ami sodorja, ugyanakkor 'A' korábbi pillanatai időbeli egymásutániságot mutatnak. Amennyiben a megnyilvánulatlan 'A' forrásban az idő folyamatosan körbeáramlik a Bindu alakú, egyoldalú felület mentén, úgy ennek látszata az időben relatív forgásként jelenik meg önmaga számára. Tehát 'A' egy olyan szálnak fogja látni magát, ami két Binduból álló pontok sorozata, s amikben az egyik Bindu ('B') mozdulatlan, a másik ('A') forog, az időben mozog. Ez lesz a csavarodó primér időszál (6. ábra), az egy dimenziós ősidő kezdeti szerkezete, lásd: Az idő szerkezete című írást.
'A' tehát azt fogja hinni, látni, hogy ő egy két Binduból álló, önmaga számára megnyilvánuló időbeli létező, aki egy szálat növeszt magából valamerre. A szál irányának itt még mindig nincs értelme, sem jelentősége. Felmerülhet a kérdés, hogy miért látja 'A' a 'B'-t végig, az időszál teljes hosszában, amikor mindig csak egy eseményhorizontjával érintkezik, ami azt láttatja vele, hogy 'B' nulla távolságra van tőle? Ez ugyanis azt jelentené, hogy az időszálat csak 'A' időben forgó képei alkotják, míg 'B' mindig ott van, ahol a szál éppen aktuális vége, a jelen, ahonnan kinő ez a furcsa "időstring". A válasz az önfelismerés illúziójában keresendő. A t1 pillanatban 'A' számára realizálódó 'B' az 'A'-ból olyan eseményhorizont hullámot indít el, amely ezt az információt, történést hordozza magán. Amikor tehát 'A' utóléri, azaz együtt halad ezzel a létezési múlthullámmal, akkor a t2 pillanatban 'A' látni fogja a t1 pillanatot, vagyis hogy meglátta 'B'-t. A t3 pillanatban pedig a t2 és t1 pillanatot, és így tovább a tn pillanatig. És ez az állapot így is marad mindaddig, míg be nem lép a "párkapcsolatba" egy harmadik játékos, összezavarva a képet.

2. HÁROM FORRÁS KÖLCSÖNHATÁSA

Annak a valószínűsége, hogy egy harmadik, 'C' forrás számára 'A' és 'B' egyszerre fognak realizálódni, gyakorlatilag nulla. Éppen ezért 'C' is hasonló önfelismerési kölcsönhatásba keveredik előbb az egyikkel, majd ehhez csatlakozik a másik forrás megpillantása, az ezzel járó összes változással és bonyodalommal egyetemben. De mi is történik ilyenkor?
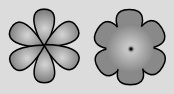
Nézzük 'A' szemszögéből 'C' realizálódásának legelső pillanatát (ez az 'A' időszálán a tn pillanat). Egy újabb időpont villan fel, szintén nulla távolságra 'A' aktuális jelenétől, azaz az időszálának végétől, mintha három Bindu lenne egy helyen. A misztikában ezt egy olyan hatszirmú virággal ábrázolják, amelyiknek nincs termőtája (7. ábra). Itt még csak egy külső, negyedik szemlélő számára van jelentősége annak, hogy 'A', 'B' és 'C' egymással milyen szögeket zárnak be, és szintén elmondhatjuk: nulla a valószínűsége annak, hogy a három pont egy egyenesre essék.

Ha ez mégis bekövetkezne, és egy egyenesre esnének, akkor az alábbi három lehetőséget kell végiggondolnunk.
1. 'C' messzebb van 'A'-tól, mint 'B'. Ekkor 'A' sosem látja meg 'C'-t, mivel annak időhullámai nem érik utól őt.
2. 'C' az 'A' és 'B' forrás között jelenik meg bárhol, miután 'A' elhaladt, mintegy "rajta keresztül". Ugyanaz a helyzet, mint az első esetben. 3. 'C' az AB egyenes másik végén helyezkedik el, mintegy az 'A' útjában. Ekkor a két ellentétes irányú időhullám megállítja 'A'-t, megfosztva őt ezzel a saját szálszerűségének látványától. Ezt követően oldalirányban óriási sebességgel lesodródik (a tangenciális hatások miatt) az egyenesről és máris az ún. "realizációs háromszög" egyik eseténél tartunk.
A realizációs háromszög 'A' szemszögéből nézve kétféle lehet: hegyesszögű vagy tompaszögű. Végeredményben hasonló következményekkel jár a két helyzet, mégis érdemes őket külön is megvizsgálni. A derékszögű háromszög esetét, mint szintén teljesen valószínűtlen helyzetet elvethetjük vagy a hegyesszögűhöz sorolhatjuk a következmények alapján. De mielőtt a külső szemlélő által látottak elemzésébe fognánk, előbb nézzük meg, mit észlel 'A' a 'C' realizálódását követő pillanatokban.
Fontos még tudnunk, hogy 'C' és 'B' egymással bármilyen (alfa) szöget is zárnak be 'C' első realizációs pillanatában 'A' felöl nézve, az ő számára ennek nem lesz jelentősége, mivel három pont egy helyen, egymásban nem teszi lehetővé a szögnek, mint tulajdonságnak az értelmezését ('A' számára). A későbbi (tn+1, tn+2, stb.) pillanatokban azonban egyből értelmezhetővé válik a bezárt szög, mint tulajdonság, ahogy 'A' új irányba kezd el sodródni az eddigi AB egyeneshez képest, és az alfa szög fogja meghatározni 'A' RV-jét.
Ha 'C' és 'B' egymással hegyesszöget zárnak be, akkor 'C' eseményhorizontja elkezdi 'A'-t odébb tolni 'B' legelső eseményhorizontjának gömbfelszínén. Ez azzal jár, hogy 'A' sebessége azonnal megnő a bezárt szögtől függő mértékben, vagyis RV>1. Ekkor viszont 'A' kilép a saját orrkupakjából, mintegy "megelőzve" önnön múlthullámait, s a maga után húzott időszála eltűnik a számára, azonnal semmivé lesz a létezés káprázatában. Nem fogja tovább látni önmagát. Helyette két pontot fog észlelni, 'B'-t és 'C'-t, önmagától nulla távolságra, s mindkettő állni fog a saját idejében. Velük fogja azonosítani önmagát éppen ezért, tehát a hatszirmú fénymag egy eszményien rövid felvillanás után azonnal újra négyszirmúvá válik. Így lesz 'A'-ból tachion, a létezés sebes vándora, aki lehagyja a saját múlthullámait (mintegy maga mögött hagyja az addigi múltját). Ekkor két lehetőséget kell figyelembe vennünk.
Az egyik lehetőség az, hogy 'A' akkor kezdte csak el kiárasztani magából az eseményhorizontjait, amikor 'B' legelső hulláma elérte őt (t1), vagyis növeszteni kezdte az önfelismeréssel járó időszálat, mintegy válaszként 'B' hatására. Ekkor 'A' RV-je maximálisan a gyök kétszeres emanációs sebességet érheti el (derékszögű realizációs háromszög esetén).
A másik lehetőség, hogy 'A' már a t1 pillanat előtt is árasztotta a saját vanását magából, és ezek a t0-ból származó eseményhorizont rétegek most megjelennek a számára, ahogy utóléri őket. Mivel 'A' jelene gyorsabb, mint a belőle áradó múltja, azt mondhatjuk, hogy a saját jövőjébe rohan. Ez így persze könnyen félreérthető megállapítás, mivel itt nem időutazásról, igazi jövőbe rohanásról van szó, hanem inkább bepillantásról a régmúlt idők "időtlen" végtelenjébe (múltba rohanás). 'A' számára tehát felvillan a saját megnyilvánulatlansága, amely (kívülről nézve) a korábban látott időszálának túlsó végén található, valahol a 'B' és 'C' által bezárt szögön belül. Így 'A'-t egyszerre három időhullám is taszítani fogja kifelé, a végtelen feneketlen sötétjébe: 'B', 'C' és önmaga. Ez ismét azzal jár, hogy hatszirmú fénymagként észleli önmagát (amiben csak az egyik Bindu mozog időben, de lassítva és hátrafelé a szubjektív időben: t-1, t-2, stb).
A két létezési és egy vanási hullám által történő taszítódás azt fogja eredményezni, hogy tovább nő 'A' RV-je, bár csak kis mértékben. A növekedés arányos lesz azzal, minél jobban eltávolodik az eredeti útirányától, az immár láthatatlan AB időszál egyenestől. Ez a sebességnövekedés azonban nem tart sokáig, és valószínűleg még azelőtt véget ér (három pont esetén), hogy 'A' kiérne a saját legelső eseményhorizont rétegéig, vagyis kikerülne a saját t0 előtt keltett (t-n) VIZéből is. A sebesség maximumát RV<gyök 3-nak becsüljük jelenleg (A pontos RV értékek kiszámításához szükséges számítógépes modellek még nem készültek el sajnos).
Az 'A' sebességének csökkenése nem áll meg a VÍZből való kiérésekor (a t-n időhullámának utólérésekor). Ahogy távolodik a többi forrástól, az őt maguk előtt sodró hullámfrontok irányvektorai által bezárt szögek is egyre csökkennek, bár a nullát csak a végtelenben érik majd el. Ezért a továbbiakban 'A' RV>1 lesz, és folyamatosan lassulva közelít az 1 felé, azt soha el nem érve.
Ha 'C' és 'B' egymással tompaszöget zárnak be, akkor azt gondolnánk, hogy 'C' hullámfrontja azonnal fékezni fogja 'A'-t, s ezzel "belelöki" a két forrás múlthullám rendszerébe. A gyakorlatban ez mégsem így történik, mert az időhullámok abszolút taszító hatásúak minden elért forrásra, és mert a (tömegtelen) források sebessége mindennemű gyorsulás nélkül, azonnal megváltozik az új interakció jelentkezésekor.
Az 'A' RV-je tehát ebben az esetben is megugrik, csak sokkal nagyobb mértékben, mint a hegyesszögű esetnél (szupergyors tachion). Az időszála szintén eltűnik előle, és önmagát (a t-n-től függően) négy vagy hatszirmú fénymagnak látva rohan tovább 'B' és 'C' időhullámai közé szorítva, az eseményhorizontjaik metszéspontjában. Közben természetesen mindkét gömbfelületen elcsúszik, ezért a három forrás által bezárt tompaszög az irányvektorok változása miatt fokozatosan csökkenni fog, míg hegyesszöggé nem válik, és innentől már tudjuk a folytatást. Ahogy azonban az 'A'-hoz tartozó alfa szög csökken, úgy csökken 'A' RV-je is, tehát a száguldása nem tart sokáig a rendszerben.
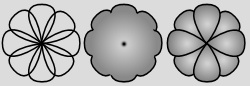
Összefoglalva az eddigieket elmondhatjuk, hogy a három időforrás interakciója végül három tachiont fog eredményezni, akik az általuk keltett hullámtér peremén egzisztálva sodródnak bele a végtelenbe. Ezen a helyzeten csak újabb források, illetve forrásrendszerek realizálódása változtathat, aminek valószínű következményei Az őskáosz és Az őskáosz időgeometriai elemzése című írásokban olvashatók. Egy 'D' forrás realizálódása 'A' számára értelemszerűen azt eredményezheti, hogy önmagát nyolcszirmú virágnak látja majd, így érthetővé válik ennek a szimbólumnak a jelentése is (8. ábra).

Készült: 2002.09.05. - 10.10.

Következő írás

Vissza a tartalomhoz