1. A PÁROSSÁG
A számegyenesen szereplő egész számokat osszuk két csoportra: páros és páratlan számokra. Páros szám az, amely osztható kettővel, páratlan szám az, amely nem. Ezek egymást váltják, ezért minden páros számnak van egy nála eggyel kisebb és egy eggyel nagyobb páratlan szomszédja. Így elvileg ugyanannyi páros számnak kell léteznie, amennyi páratlannak. Vagy mégsem?

Logikus, hogy a nulla, ami a -1 és a +1 közti helyet foglalja el, páros szám. Mivel 1-el nagyobb a -1-nél és 1-el kisebb a +1-nél. Ebben az esetben viszont eggyel több páros számunk van, mint páratlan, mert minden pozitív egész páros számnak van egy negatív egész páros szám társa és minden pozitív egész páratlan számnak van egy negatív egész páratlan szám társa. A nullának vajon mi lehet a társa? Csakis egy másik, előjel nélküli szám...
Ha a számegyenest számkörré alakítjuk, akkor a kör nullával szembenlévő oldalára a végtelen kerül. A számkörön nincs értelme a pozitív és negatív végtelennek (egy helyre esnek), így a nulla mellett a végtelen lesz az a másik szám, amelyiknek nincs előjele. Ha a nulla páros, akkor a végtelennek páratlannak kell lennie.
2. SZUPERPRÍMEK
Vajon a végtelen prímszám-e? A prímszám csak önmagával és 1-el osztható maradék nélkül (a természetes számok halmazán belül). Egy prímet önmagával osztva 1-et kapunk, 1-el osztva önmagát kapjuk. Ha elosztjuk a végtelent bármely (nála kisebb) véges számmal, mindig önmagát kapjuk. Így egyrészt a végtelen minden számmal osztható maradék nélkül, másrészt egyikkel sem, mert az osztás eredményeként nem kapjuk meg az osztóit. A végtelen tehát egyfajta "szuperprímszám" lesz.
Van még egy másik ugyanilyen szuperprímszám is, a kettő. A kettőre szintén az érvényes, hogy minden nála kisebb természetes számmal maradék nélkül osztható, ugyanakkor csak önmagával és eggyel osztható.
Vajon a végtelen ikerprímszám-e? Az ikerprímszámok azok, amik különbsége kettő. Ilyen a 3 és 5, 5 és 7, 11 és 13, stb. Mivel nincs a végtelennél nagyobb szám, csak kisebb, ezért inkább azt kell megvizsgálnunk, hogy a végtelen-2 szintén prímszám-e? Bármely véges számot kivonva a végtelenből mindig végtelent kapunk, tehát a válasz: igen. Sőt, itt egy prímszám sorozatot kapunk, ami végtelenül hosszú, s közben mégiscsak pontnyi méretű! Olyan, mint az időfizikai teremtésmodellből jól ismert időszál.
Ennek minden eleme prím. Nemcsak a páratlanok, hanem a párosak is! A végtelen-1 ugyanis szintén végtelen! Ezzel bizonyítottuk, hogy végtelenül sok prímszám és ikerprím létezik!

3. KVÁZIVÉGTELEN SZÁMOK
A végtelenből bármely véges számot kivonva végtelent kapunk. Amennyiben azonban nem végezzük el a műveletet, csak felírjuk, látszólag egymástól különböző számokat kapunk. Így logikusnak tűnik, hogy a végtelen-1 nagyobb, mint a végtelen-2. Vizsgáljuk meg ezen "kvázivégtelen" számok tulajdonságait az ábrázolhatóság szempontjából.
A végtelen a számegyenesen meghatározhatatlan helyen található. A matematikusok szerint nincs is rajta a számegyenesen. A számkörön azonban meghatározható, kijelölhető a helye, pontosan a nullával szemben, így ezen rajta van! A végtelen pontjához viszonyítva kijelölhetők a végtelennél véges értékkel kisebb, kvázivégtelen számok is. A számkörön végtelenül sok olyan pozitív és negatív kvázivégtelen szám található, ami kisebb, illetve nagyobb az abszolút végtelennél.
Az eredmény: egy olyan számkör, amelyen két viszonyítási, kiindulási pontunk van. Ezekből két "számfélkör" indul ki, amik ugyan elvileg összeérnek, valahol az ábrázolhatatlanság tartományában, mégsem végezhetünk problémák nélkül számtani műveleteket közöttük. Tulajdonképpen ez a két számfélkör végtelenül messze van egymástól.
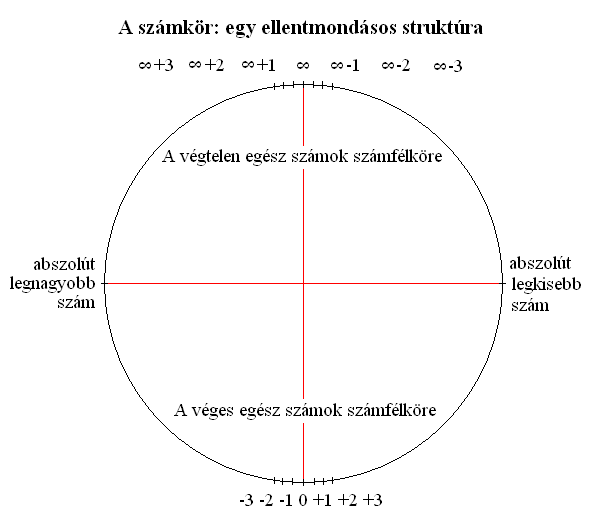
A számkör, ami filozófiailag hasonló az időfizikából ismert időhurokhoz, egy ellentmondásos matematikai struktúra. Itt a végtelen+1 szám negatív szám lesz, ezért bár közelebb van a nullához, mint a végtelen, mégis nagyobb a végtelennél. Melyik lehet akkor az "abszolút legnagyobb" szám a számkörön? Elsőre azt gondolnánk, hogy végtelen+végtelen = abszolút legnagyobb szám. Ez azonban nem ábrázolható a számkörön, ezért a végtelenhez csakis véges számot adhatunk hozzá. Végtelen+legnagyobb véges szám = abszolút legnagyobb szám. De hol van ez?
Az abszolút legnagyobb számnak valahol félúton kell lennie a nulla és a legkisebb negatív szám között. Ha viszont van abszolút legnagyobb szám, lennie kell abszolút legkisebb számnak is, ami logikus, hogy a számkör ellenkező pontján található és pozitív szám lesz.
Mivel a végtelen-végtelen = 0 nem a számkör túlsó oldalán van, ezért ismét ellentmondásba futottunk. Ha ugyanis a végtelen+végtelen = 0 műveletet érvényesnek tekintjük, el kell fogadnunk, hogy a nulla a legnagyobb és legkisebb szám is a számkörön. Ebben az esetben viszont a számkörünk összeomlik egyetlen ponttá és kezelhetetlenné válik.
4. IDŐMATEMATIKA
Mielőtt tovább mennénk, kell egy aprócska filozófiai kitérőt tennünk. A matematika axiómarendszerét úgy alakították ki a matematikusok, hogy ellentmondásmentes és determinisztikus legyen. Tehát benne egy adott művelet csak egy adott eredményre vezethet, illetve nem lehet benne egy állítás egyszerre igaz és hamis. Ez a feltétele a rendszer logikájának, használhatóságának, ami nélkül az egész összeomlana és értelmét veszítené. Ennél fogva a fenti okoskodás, mivel ellentmondásba vezet, szükségképpen hibás kell legyen. Szakértő matematikusok nyilván szépen meg tudják indokolni, több ponton is, hogy hibás volt a levezetésem a nullát és a végtelent illetően. Lásd: a 6. fejezet észrevételeit. Csakhogy!

A teremtés, a létezés önnön teljességében ellentmondásos. Ezt tudjuk, nem is lehet másmilyen. A létezés így alapjaiban az ellentmondásosságra épül, nem holmi (bármilyen) logikára, de a létezés működésében mégis van logika. Amely logikával bármely tetszőleges részrendszere (pontatlanul, tehát hiányosan) leírható, modellezhető.
A jelenleg hivatalosnak minősített, mereven ellentmondásmentes (csak véges számokkal operáló) matematika segítségével tehát nem fejezhető ki, nem ábrázolható a létezés, a teremtés. Ezért nem sikerült a mai napig sem használható matematikai formulákat alkotni az időfizikai fogalmakra, jelenségekre (időhurok és társai). Ez sok kutatónak kedvét szegte, a filozófusokat kivéve. Szükségessé vált tehát egy másfajta, ellentmondásokon alapuló matematikai struktúra megalkotása, amelynek bármely tetszőleges részrendszere logikus, de egészében mindig ellentmondásokra vezető. Ez az időmatematika, ami filozófiai alapjaiban másféle, rugalmas megközelítésből kiindulva képes tárgyalni a teremtés jellemzőit.

Az időmatematika alapjainak meghatározása egyelőre még folyamatban van, de idővel remélhetőleg alkalmassá válik majd az időfizikai jelenségek leírására, kezelésére. A témáról bővebben majd egy külön írásban fogunk beszámolni. És most térjünk vissza eredeti témánkhoz, a végtelenhez.
5. A SZÁMJEGYEK
A végtelen egy olyan szám, amely nem ábrázolható számjegyek sorozataként, mivel ez végtelenül hosszú lenne, amihez végtelen sok hely kell (papír, tinta, munkáskéz, stb.) és idő a felírásához. Felmerül a kérdés, hogy a végtelennek, amennyiben mégis ábrázolni kívánjuk legalább egy véges méretű, tehát végtelenül kicsiny, elenyésző részét számjegysorozatként, vajon milyen szám lehet az utolsó jegye? Az, amelyik az egyes helyiértéket foglalja el.
Minden véges egész szám adott darab számjegyből áll, melyek az egyes helyiértékeket reprezentálják a számrendszerben. A 10-e számrendszerben adott helyiértéken a legnagyobb számjegy a 9-es, ezért az adott hosszúságú, adott darab számú jegyből álló számok között a legnagyobb az, amelyik csupa 9-esből áll. Ezek szerint a végtelennek végtelen számú 9-esből kell állnia. Mivel pedig a végtelen nem tartozik az egész számok közé, törtszámnak kell tekintenünk, tehát a tizedesvessző mindkét oldalán végtelenül sok 9-est kell ábrázolnunk.
...999,999...
Sok egyéb mellett van ezzel egy olyan gond, hogy a 9, 99, 999 stb. számok egyike sem prím, mert 3-mal és 9-cel egyaránt oszthatók. Az abszolút végtelen ezért nem minősíthető rendes prímnek, hanem szuperprímnek. A kvázi végtelen számok azonban lehetnek rendes prímek is, nem csak szuperprímek, mert más számjegyeket is tartalmazhatnak a 9-esen kívül. A 19, 29, 59, 79, 89 például prímek. A számegyenesen a (pozitív) végtelen felé haladva nagyjából ugyanannyi véges egész prímszám végződik 1, 3, 7 és 9-re.
A 9-re végződő rendes prímszámok hátulról második jegye (a 10-es helyiértéken) bármilyen szám lehet. Én csak 450-ig vizsgáltam őket, de már itt is úgy találtam, hogy nagyjából egyenletes eloszlásban találunk minden számjegyet a prímek második jegye helyén: 0,1,2,3,4,5,6,7,8,9. Valószínűsíthető, hogy a hátulról harmadik, negyedik, stb. jegyek is mindenfélék lehetnek ennek alapján.
Így elmondhatjuk, hogy a kvázivégtelen számok bármely helyiértéken bármely számjegyet tartalmazhatják. Csupán annak a kritériumnak kell megfelelniük, hogy végtelen számú számjegyből kell állniuk.
6. AZ EDDIGIEK KRITIKÁJA
A gondolataid jók, hogy megpróbálsz rámutatni mennyiségekkel kapcsolatos definíciók másféle módú értelmezhetőségeire. Azonban azt vedd figyelembe, hogy a matematikában a végtelen halmazok nem a diszkrét, egész számokból álló halmazoknak, hanem inkább a valós számok halmazának feleltethetőek meg.
Az az igazi végtelen, ahol egymáshoz bármilyen közel lévő A, B pont között (A != B) még mindig van egy olyan C pont, amire igaz, hogy A<C<B. Az általad folyton boncolgatott egész számok csupán megszámlálhatóan végtelennek minősülnek. Ez az elmélkedésben is sokszor látszik, hogy te a végtelen alatt mindig a leírhatatlanul kurvanagy számokat érted. Pedig szerintem nem erről volna szó. A valós számegyenesen ugyanolyan végtelennek számít a [0,1] intervallum is, mint az egész valós számok halmaza.
A 2-es és 3-as pontod játék a definíciókkal. A végtelent szerintem értelmetlen hasonlítgatni, nincs olyan szám, hogy végtelen-2. A számkörön nincs rajta a végtelen, mert a számkör azon pontja, ahol a végtelent gondolod gyakorlatilag nem létezik, (a számkörön ott egy végtelenül piciny "lyuk" van), persze tetszőlegesen közel lehet menni hozzá, de elérni nem lehet. Nincs végtelen szám. Ez olyan mint a 0-val való osztás. Vedd az egész számok és a reciprok számok számkörét, és gondold tovább. Ilyen formán ez értelmetlen, de NEM ellentmondás, hanem egyszerű logika, szerény véleményem
szerint.
A 4-es pontod felkeltette az érdeklődésemet, mégsem mondtál el semmit. Ez már egy ellentmondás. Mondtál is meg nem is... A bizonyítások során, az egyszerre igaz és hamis állítások arra jók, hogy jelzik egy feltételezés hamisságát. A hamis állításokból igaz és hamis állítások is következhetnek. Az okoskodásod nem ellentmondásos, szerintem.
"A jelenleg hivatalosnak minősített, mereven ellentmondásmentes matematika segítségével tehát nem fejezhető ki, nem ábrázolható a létezés, a teremtés. Ezért nem sikerült a mai napig sem használható matematikai formulákat alkotni az időfizikai fogalmakra, jelenségekre (időhurok és társai). Ez sok kutatónak kedvét szegte, a filozófusokat kivéve."

Erre hadd mondjam azt, hogy inkább a megfelelő képzettség és szabadidő hiányában vagyunk képtelenek előrejutni. Magamból indultam ki, már totál új szemlélettel állnék az egész kutatáshoz, ha volna rá időm. Nem gondolhatod komolyan, hogy pont a matematika tudományát kell megreformálni. Még mindig ebben hiszel/hisztek? Én inkább félnék a dogmává rögösödött téves elképzelésektől, amik ellepték a rendszert. Hosszú az út, míg egy feltételezésből tény kerekedik.

Sajnos azt látom, hogy a matematika által biztosított eszközök töredékét kipróbáltátok - elméletben, és nemvárt eredményre jutottatok, vagy rosszabb esetben nem jutottatok eredményre. Ha tudsz ellentmondásos rendszerre bármit is felépíteni, akkor arra kíváncsi leszek azért. :)

5-ös pont: erőlködés a bazinagy számokkal, mint a 2-3-as pontban.

7. VÁLASZOK A KRITIKÁRA
Pont azért írtam ezt a kis elmélkedést, mert feltűnt, hogy a matematikában igyekeznek kerülni a végtelen halmazok egész számokon való alkalmazását. Miért? Ki gátolja meg, hogy errefelé kutakodjunk?
Természetesen én is tudom, hogy a valós számok számegyenesén bármely véges szakasz a végtelenségig osztható. Bármely tetszőlegesen kicsiny szakaszon végtelenül sok irracionális szám fér el, de itt most nem ebbe az irányban akartam tovább gondolni a dolgokat. Nem lefelé, hanem felfelé terjesztettem ki a számegyenest a végtelenségig.
Mi az, hogy nincs végtelen-2? Ha a végtelen, mint szám létezik, márpedig van ilyen fogalom (és rá a fekvő nyolcas alakú jel), tehát léteznie kell, akkor azzal műveleteket is lehet végezni. A végtelent nem létezőnek tekinteni kényelmes megkerülése a problémának. Csupán értelmezés kérdése, hogy miként állunk hozzá a végtelen tulajdonságaiból fakadó ellentmondások jelentette kihívásnak. A megszámlálhatóan végtelen halmaz fogalma is arra utal, hogy a végtelen rajta van a számegyenesen, tehát létező dologról van szó.
A számkörön lévő végtelenül piciny lyuk az, ahol az izgalmas dolgok vannak. Ez az ismeretlen tartomány, ahová bátorság kell belépni. Kutatni csak az ismeretlent lehet. Az ismert kutatása nem kutatás, hanem ismétlés.

Miért ne lehetne megreformálni a dolgokat? Had próbáljuk meg! Hátha sikerül! Tán még valami hasznunk is lehet belőle. És ha nem sikerül, akkor sincs gond, csak a saját időnket pazaroltuk, nem a tiédet. Pont azért szívózunk ilyesmikkel, mert az eddigi eredményeink nem voltak kielégítőek. Az ellentmondásos alapra épülő rendszer készítése pedig folyamatban van, majd egy külön írásban bemutatjuk az ezzel kapcsolatos elképzeléseinket.

Legutóbbi módosítás: 2006.04.25.
Következő írás
Vissza a tartalomhoz