1. BEVEZETÉS
Ahogy az időfizikai és időmatematikai modellek eredményei bekerülnek az alkalmazott tudomány területére, és megkezdődik a gyakorlati hasznosításuk, teljesen új technológiák fognak létrejönni. Csupa olyan dolog, amiről eddig csak a fantaszták álmodtak, és még több olyan, amit elképzelni sem lehet előre. Mindezek összefoglaló megnevezésére alkottuk meg az emanika szót, ami az emanációs technika rövidítése.
Az emanika lényegében a gravitációs hullámok észlelésével, mérésével, felhasználásával és kutatásával kapcsolatos műszaki tudományág (tértechnológia). Ide tartoznak a gravitációs távcsövek és mikroszkópok, spektrál analizátorok, diagnosztikai berendezések és navigációs rendszerek, amik már évek óta fejlesztés alatt állnak. A későbbiekben pedig ide fogják majd sorolni az erőtérpajzs generátorokat, mesterséges gravitációt keltő generátorokat, gravitációs számítógépeket, gondolatolvasó gépeket, valamint a különféle teremtőgépeket és a mindenféle térmanipulációs, térváltó és térkonverziós berendezéseket. Ilyen műszaki fejlesztések nélkül gyakorlatilag nem lehet rendes űrtechnikát fejleszteni, ami alkalmas a bolygóközi közlekedés mellett a csillagközi utazások megvalósítására is.
Ezzel az írásunkkal egy sorozatot szeretnénk elkezdeni az Eseményhorizonton, amiben sorra bemutatjuk a különböző jövőbeli berendezések működésének elméleti alapjait, emanikai jellemzőit. Bízunk benne, hogy hasznos tippeket tudunk majd adni a fejlesztőknek és kísérletezőknek a munkájukhoz és ők cserében ezért megosztják velünk a gyakorlati eredményeiket, megerősítve vagy cáfolva az előzetes elgondolásainkat.
Mivel ebben az írásban az emanika alapjait szeretnénk bemutatni, arra gondoltunk, hogy először megismertetjük az Olvasókat a gravitációs hullámok érzékelésével, mérésével kapcsolatos néhány problémával.
2. MÉRÉS A GRAVITÁCIÓS TÁVCSŐVEL
A gravizor mérőrúdja egy elektromágnesesen szigetelt, zárt cső, a két végében piezókristályokkal. A csőbe elvileg csak a gravitációs hullámok juthatnak be, feltéve, hogy a berendezés a mechanikai rezgésektől szigetelt talapzaton áll. A cső elforgatásakor a hossztengelye felé található gravitációs források rezgésváltozásainak futási késedelme eléri a maximumát. Ennek segítségével a minden irányból egyszerre érkező általános háttérzaj leszűkíthető két irányra. Az irányérzékenység a gyakorlati mérések szerint kb. tizedfokos, ami már lehetővé teszi a nagyobb égitestek részletes vizsgálatát.
Felmerül a kérdés, hogy lehet az érzékelő segítségével egyszerre csak egy irányba látni? Mivel a gravitációs hullámok mindenen áthatolnak és leárnyékolhatatlanok, csak az univerzumban megfigyelhető hullámképi aszimmetria segítségével választható szét egymástól a két irányból érkező jel. Ezen aszimmetriát kozmikus méretekben az okozza, hogy egyrészt az univerzumban az anyag eloszlása nem egyenletes, másrészt a Föld nem a világtojás közepén van. Így a gravitációs háttérzaj minden irányban teljesen egyedinek mutatkozik. Ezt lehet kihasználni a mérések pontosításához.
Az első módszer, hogy két vagy több gravizorral kell különböző helyekről, egy időben mérni ugyanazt a célpontot és számítógéppel egyesíteni az adatokat. A két észlelési nyaláb által bezárt szög miatt a négy irányból érkező jelhalmaznak az lesz a közös része, ami a metszéspontból érkezik. A többi háttérzajként leszűrhető.
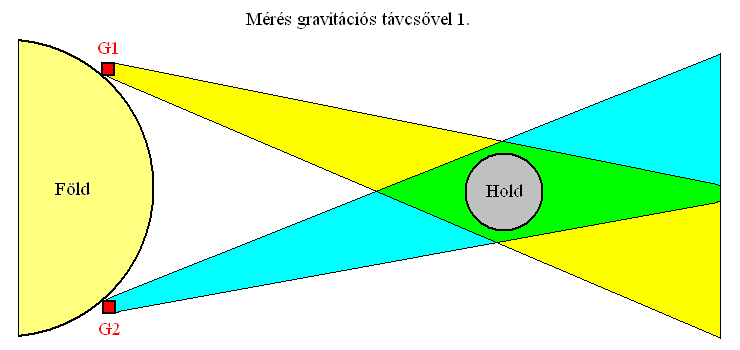
A fő gondot itt az okozza, hogy ha a célpont messze van, a két nyaláb által bezárt csúcsszög kicsi, a fedési kettőskúp pedig hosszú, amiben igen sok más dolog is benne lehet zavaró hatásként (másik bolygó, csillag előtte vagy mögötte, relatíve közel a célhoz). Az észlelési nyalábok vastagsága, vagyis a műszer irányérzékenysége pedig nem csökkenthető akármeddig, így egy határon túl a táguló nyalábok nem válnak szét. Az univerzum végéig (a neutronfalig), mondhatni a végtelenségig együtt futnak a térben. Ez a probléma az optikai csillagászatban a parallaxis segítségével végzett távolságmérésnél jelentkezik. Így egyidejű mérésnél a Föld átmérője, fél éves késleltetésnél a Földpálya átmérője korlátozza a legnagyobb "belátható", illetve azonosítható távolságot. A későbbiekben, ha rendes űrtechnikánk lesz, szondákra pakolt gravizorokkal sokkal messzebbre is elláthatunk majd. Csak ki kell küldeni őket a Naprendszer szélére, egészen a térbúráig, aminek átmérőjét 14-15 milliárd kilométeresnek becsüljük jelenleg (pontos mérések még nem állnak rendelkezésre).
Ha közeli tárgyat mérünk a műszerrel, akkor a nagy parallaxis a szabálytalan testek vizsgálatakor okoz gondot. Mivel nem ugyanolyannak látja a két vevő a különbségeket. Optikai megfigyelésnél ez nem okoz gondot, de gravitációs mérésnél igen, mert a bejövő jel elemzését a számítógép végzi. A két kép közti különbséget pedig szükségképpen levonja az egészből, tehát marad a test belseje, elmosódó kontúrokkal.
Ezen a bajon csak kis távolságok esetén lehet segíteni (például gravitációs mikroszkópnál), ahol több érzékelőfej alkalmazásával mérhető a hullámok görbülete és ezzel megadható a szűrésnél egy plusz-minusz távolsági korlát, amelybe a cél beleesik. Nagy távolságnál a görbültség mérhetetlenül kicsinyre csökken.
A másik módszer lényege, hogy egy (vagy két) gravizorral kell különböző időpontokban mérni ugyanazon célpontot és összehasonlítani az adatokat. A távcső ugyanis mozog a Földdel együtt a világűrben, ahogy a céltárgy is. A kettő között és a céltárgy mögött az észlelési nyalábba belógó objektumok is elmozdulnak idővel, így a két mérésnél jó eséllyel más lesz a kiszűrésre szoruló háttérzaj.
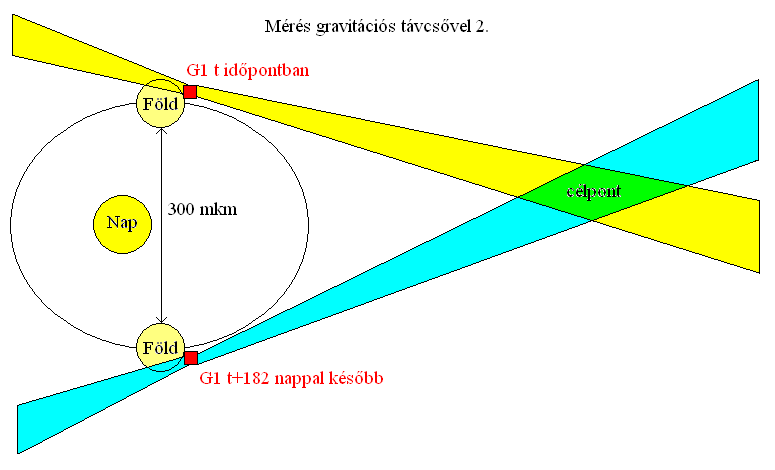
Ezen megoldás esetén sajátos kivételt (és egyben problémát) jelent viszont a Föld a talpunk alatt. A bolygó ugyanis nem változik jelentősen a két mérés során, így ha tömege beleesik a nyalábokba, már rátelepszik a képre (kiszűrhetetlenül). Tehát vagy horizontálisan kell mérni egy magaslatra helyezett berendezéssel vagy ki kell tenni az egészet az űrbe, távol mindentől. Ezzel a módszerrel a Föld belseje viszont könnyen vizsgálható teljes mélységében.
Amint az látható, lényegében mindkét módszer ugyanazon alapelvre épít: sok mérést kell végezni térben és időben, majd összehasonlítani őket és kivonni a változásokat. Ami megmarad, az lesz a céltárgy (bolygó, csillag) stabil gravitációs színképe.
Készült: 2005.06.23.
Következő írás
Vissza a tartalomhoz