1. BEVEZETÉS
Bármely halmaz vagy elem meghatározható tulajdonságai (jellemzői, paraméterei) minimálisan két állapotot vehetnek föl a szemlélő számára. Ez az egy bitnyi információ, ami leírja, hogy a szemlélt dolog rendelkezik-e egy adott tulajdonsággal. A bit (binary unit) információelméleti alapegység, ami a hír információtartalmának számszerű mennyiségét fejezi ki. Ez a hírben szereplő állapot valószínűségének kettes alapú negatív logaritmusa. Egy bit tehát egy 50%-os valószínűségű esemény bekövetkezéséről vagy elmaradásáról tudósít.
A létfilozófiában az egy bitnyi információ maga a létezés: az, hogy a szemlélt pont létezik (a bit értéke: egy) vagy nem (a bit értéke: nulla) a szemlélő számára. Egy pont önmagában megnyilvánulatlan, mert senki sem látja és ő sem látja önmagát. Ezért nincs semmilyen paramétere, semmit sem mondhatunk róla. Két pont egymás számára megnyilvánul, mert látják egymást és van egy bitnyi jellemzőjük: léteznek. Az egy bitnyi információnak még nincs mértéke, mert nincs mihez mérni, nem lehet semmivel összehasonlítani. Az egy bitnyi információ éppen ezért nem tekinthető valódi információnak (ismeretnyereségnek), nevezzük tehát protoformációnak.
Három pont egymás számára történő megnyilvánulása már lehetővé teszi a különbségtételt az összehasonlítás miatt. A szemlélő számára az egyik ilyen, a másik olyan. A továbbiakban jelöljük ezt a három pontot A, B és C betűkkel és vizsgáljuk meg a kölcsönhatásuk következményeit.
Két időben létező pont egymáshoz képest eltérő sebességgel foroghat, amit ők kölcsönösen érzékelnek is, de a forgás iránya (balos vagy jobbos) nem határozható meg a számukra, mert nincs mihez viszonyítaniuk. Három pont esetében azonban lehetőség van összehasonlítani a forgások sebességét és irányát, sőt a szálirányú elmozdulást is (közeledés vagy távolodás). A három pontot hívjuk szentháromságnak, amiben értelmezhetővé válnak a különbségek, s ezáltal megszületik az információ, az aszimmetria és a mérték fogalma.
Bármelyik pontból (ez legyen A) szemléljük is a másik kettőt, azok tulajdonságait a visszacsatoláson keresztül önmagammal (A tulajdonságaival) összehasonlíthatom. A másik két pont ennek megfelelően lehet azonos velem: AAA, különböző tőlem, de azonos egymással: ABB, azonos velem az egyik és különböző a másik: AAB, és különböző tőlem és egymástól is: ABC. A négy lehetőségből csak három a valódi, mert ha áthelyezem a szemlélőpontomat A-ból B-be, akkor az ABB és AAB állapotok azonosnak tűnnek (tükröződések). Így tehát a három pont három féle állapotban lehet egymás számára.
Ahhoz, hogy az idő, mint állapot változás értelmezhető legyen, minimálisan három időpontra van szükség. Ahhoz, hogy a tér, mint kiterjedés (hely és helyzet) értelmezhető legyen, minimálisan három térpontra van szükség. Az idő és a tér a létezés kiterjedésének kétféle értelmezése, vetülete, amiket praktikusan használni szoktunk. Ezeken kívül még n féle további vetület hozható létre, de mi most elégedjünk meg ezzel a kettővel, amikre a matematikában és a fizikában általában szükség van az egyszerűbb jelenségek modellezéséhez.
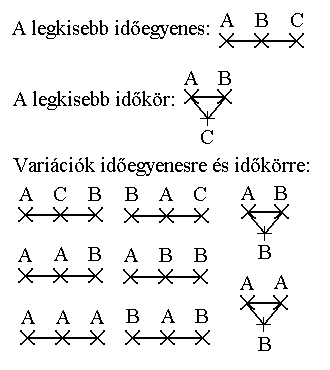
2. A KITERJEDÉSI TÉTELEK
Első lépésként fogalmazzuk meg tételszerűen az időmatematika alaptörvényeit.
Három pont tétel: A legkisebb kiterjedés szálirányban három pontnyi. Ezt hívjuk a továbbiakban egy dimenziónak. A jelölése röviden: 1D a továbbiakban.
A kiterjedésnek két fajtája (vetülete) van: térdimenzió és idődimenzió.
Dimenzió tétel: A kiterjedés egy pont meghatározott irányokba történő transzformációja, elmozdulása a létezésének valamely vetületén. A dimenziókat hívjuk a továbbiakban változóknak is.
Az irányok kétfélék lehetnek: skalárisak (minden irányba történő elmozdulás egyszerre) és vektoriálisak (egy irányba történő elmozdulás egyszerre).
A transzformációk (átalakítások, leképzések) kétfélék lehetnek: mennyiségi (méretbeli) és minőségi (formai).
Az elmozdulások kétfélék lehetnek: forgás körben (szálszerű tengely körül) és futás egyenesen (szálirányban).
A vetületek kétfélék lehetnek: időbeli (a pont elmozdulásai) és térbeli (a pont helyzete a beágyazási környezetében). A két vetület egymás duálpárja. Az időbeli elmozdulás térbeli helyzetekkel (realizációs irányokkal) ábrázolható, a térbeli helyzet időbeli elmozdulásokkal (realizációs késedelmekkel) ábrázolható. Ezen duális leképzési módszereknek köszönhető, hogy egyesíteni lehet a különféle időfizikai modelleket az időmatematikai modellekkel úgy, hogy egymást támogatják és kiegészítik.
Az időmatematikában a transzformációkat kétféle megközelítésben vizsgáljuk. Az egyik az időgeometria, mely a kiterjedések formai tulajdonságaival foglalkozik, a másik az időtopológia, mely a kiterjedések határainak formafüggetlen tulajdonságaival foglalkozik. Ezek alaptörvényeit részletesen lásd a Forma és felület című publikációban.
Az alábbiakban csak a három pont tétel és a dimenzió tétel következményeivel foglalkozunk részletesen.
3. AZ IDŐBELI KITERJEDÉS
A fizikai objektumok (és alkotóik) a térbeli kiterjedésük mellett időben is léteznek, vagyis nem tekinthetők pusztán elméleti konstrukcióknak. Ahhoz, hogy ábrázolhassuk őket, az időtopológiai és időgeometriai konstrukcióinknak időbeli változásra képes, dinamikus struktúrákat kell alkotniuk, amik révén a valódi dolgok (tárgyak) modellezhetők időfizikailag. Ehhez persze szükség van az időmatematika és az időfizika világa közti kapcsolatot biztosító leképzésekre, hogy az elméleti konstrukcióink a gyakorlatban is használhatók legyenek.
A térbeli dolgok mozgása, tulajdonságainak megváltozása (deformációja) időbeli jelenség. A pont időben létezik, ami a forgással ábrázolható. Az álló pontot holtpontnak hívjuk, mert időtlen, míg a forgó pontot létezőnek, azaz élőlénynek nevezzük. Az élőlény az élő létezvény összevonását jelenti ebben az értelmében. Az időnek pedig mindig telése van, sosem múlása, mert az idő nem múlik el, nem szűnik meg. Még a kibocsátó forrásának megszűnése után sem, mivel kiáradó hullámai megmaradnak a végtelenségig tágulva a saját origójukhoz képest. Az elmúlás kifejezést ezért csak abban az értelmében szabad használni, hogy egy szemlélőpont számára a rajta áthaladó és tőle távolodó időhullámok elmúlnak, tovább terjednek a saját múlthullámaival együtt.
Minden mozgás kiterjedést, beágyazási környezetet igényel a mozgó objektum számára. A pont mozgásához legalább 1D-s közeg kell, azaz egy egyenes vagy kör (vonal). Ha a pont időbeli mozgását térben ábrázoljuk, a mozgás minden pillanatát (minden elfoglalt helyzetét) egymásra szuperponálva, akkor egy nyúló egyenest: élt kapunk. Ez, mint a neve is mutatja magyarul: élő megnyilvánulás (dinamikus létező).
Mivel a pont mozgásának iránya (praktikus megállapodás szerint) megegyezik az egyenesen az idő telésének irányával, ezért az időegyenes már aszimmetrikus lesz. Ennek köszönhető, hogy minden kiterjedéssel rendelkező objektum a legkisebb három pontos minimálszakasztól és minimálkörtől kezdve az nD-s végtelenségig aszimmetrikus szerkezetű valamilyen formában.
Az egyenes aszimmetriája arra a tulajdonságára vonatkozik, hogy az egyik végétől indul és a másik irányba nyúlik. A nyúlási végen van a jelen (tn), a kiindulási végen a legelső időpillanat (t0). A két pont között az egyenes a végtelenségig tágul, azaz megtelik (közbülső) időpontokkal. Ezért telik az idő, s nem múlik. A két végpontra szavunk is van: végpont (mélypont) és csúcspont (tetőpont). A növények is a csúcsuk felé nőnek, nyúlnak, mint helyhez kötött (egy pontból, a magból kiinduló) élőlények.
Az él irányultságát (amerre a csúcsa mozog) a térben vektornyíllal ábrázoljuk, melynek alkotói a következők.: Van vége (talpa), csúcsa (a nyíl feje), hossza (nagysága) és iránya (a beágyazási környezetében). Az irányított szakaszt nevezzük nyílnak vagy irányvektornak, az irányított félegyenest pedig sugárnak. A vektorok segítségével a nagyobb dimenziószámú objektumok is irányíthatóak (mozgathatóak, deformálhatóak), s ezzel dinamikus létező objektumokká válnak. A holt, időtlen és statikus matematikából így válik élő időmatematika, amely már alkalmas a fizikailag létező dolgok hatékony modellezésére.
Mivel az időbeli létezés folytonos, minden időben véges objektum a létezésének bármely pillanatában leképezhető egy vektornyílra, melynek hossza arányos a létezésének időtartamával. Fizikailag ez megfelel annak a ténynek, miszerint például egy 1 millió éve létező (tetszőlegesen kicsiny) kődarab létezési mérete (hullámtere) 2 millió fényév átmérőjű, mivel a létezésének információ tartalma gömbszerűen árad ki belőle a környezetébe. A nyelvünkben erre utal szemléletes módon a nagyszülő kifejezés. A nagy szülők (nagyapa, nagyanya) azért neveztetnek nagynak, mert ténylegesen nagyobb a létezésüket ábrázoló, tartalmazó eseményhorizont gömb sugara, mint a szülőknek (kismama).
Idődimenziószám tétel: Egy vizsgált rendszer idődimenzióinak száma a külső szemlélőpontok számának felel meg, akik számára létezik.
Az időről tudjuk, hogy skaláris mennyiség a fizikában, vagyis minden irányba kiterjed a forrásától egyszerre. Ezen irányok megfelelnek egy n dimenziós kör összes lehetséges sugárvonalainak, amikkel az origó összeköthető bármely felületi (határoló) ponttal. A sugár tehát meghatározza a létezés eseményhorizont gömbjének felületét az origó körül. Az így kapott időgömb felszíne egyenidejű, és mivel minden elért pontot csak egy pontban tud megérinteni (egy rétege), ezért egyszerre, egy szemlélő számára mindig egy idődimenziósnak mutatkozik.
Az időgömb térdimenzióinak száma ellenben attól függ, mennyi a forrás (kibocsátó objektum) térdimenziószáma, azaz hány szálú térkereszt illeszthető a pontjaira. Ennek elméletileg szintén nincs felső korlátja, ahogy az idődimenzióknak sem.
A teljes létezés (minden létező) együttes időgömbje tehát n-1 térdimenziós és n-1 idődimenziós. Azért nem nD-s, mert az origó pontja önmagában 0D-s (függetlenül attól, hová rakjuk az egészen belül). Mivel pedig a létezés maga időben nem korlátozott (hisz ő maga az idő), ezért a kiterjedése, mozgása mindig egy félegyenes mentén történik. A puszta létezésnek önmagában tehát nem nyila, hanem sugara van. Ez a sugár természetesen bármely pillanatban egyenértékűnek tekinthető egy vele megegyező hosszúságú nyíllal.
4. A TÉRBELI KITERJEDÉS
Térdimenziószám tétel: Egy vizsgált rendszer térdimenzióinak száma az egymásra merőleges legkisebb kiterjedéseknek felel meg.
A merőlegesség definíciója a geometriában a következő.: Két egyenes akkor merőleges egymásra, ha az egyiket a másikra tükrözve az előbbi önmagába megy át. A kiterjedéseknek azért kell egymásra merőlegesnek lenniük, mert ez a legnagyobb szög (kitérés, mozgásirány különbség), amit két egyenes bezárhat egymással. Ebben az esetben a tompaszögeket nem tekintjük valódi szögeknek, mivel ezek a hozzájuk tartozó hegyes szög kiegészítő szögei. Bármely véges objektum vagy kvázi végtelen méretű beágyazási környezet dimenziószáma meghatározható tehát azzal, hogy az alkotó pontjaira hány darab egymásra merőleges egyenest tudunk ráilleszteni.
A hangsúly a ráillesztésen van, nem a lefedésen. Nem azt kell vizsgálni, hogy az objektumot alkotó pontok hány darab egymásra merőleges egyenest képeznek egymással, mert a dimenziószám szempontjából lényegtelen, hogy az objektum folytonos vagy nem. Tehát a vizsgálat a nem összefüggő rendszerek egymáshoz viszonyított helyzetének (térbeli irányának) meghatározására is alkalmas. Ez teszi lehetővé, hogy egy objektumnak kétféle dimenziószáma legyen: globális (hány dimenziós egészében) és lokális (hány dimenziósak az egyes részei). A témával részletesen az időtopológiai publikációkban foglalkozunk.
A térdimenziószám meghatározására használt, egymásra merőleges egyeneseket a számuktól függetlenül térkeresztnek hívjuk. A koordináta geometriában megszokott jelöléseket megtartva az egyeneseket sorrendben ezekkel a betűkkel jelöljük: XYZVUTSRQP... stb. A koordináta-rendszerben hozzájuk rendelt számok a térkiteljesedési változók, melyek révén az origóhoz képest meghatározható az objektumok helyzete.
A térkereszt segítségével előállítható objektumok sorozatát a Merőlegesség n dimenzióban című írásban ismertetjük.
5. A MINIMÁLSZAKASZ
A szakasz csak abban különbözik az egyenestől, hogy véges hosszúságú. Ha az egyenes egy dimenziós kiterjedésű, akkor a szakasznak is 1D-snek kell lennie. Vajon hány pontból kell minimálisan állnia a létező legrövidebb szakasznak ahhoz, hogy már igaz legyen rá a szakasz definíciója? A téma előzményét részletesen lásd: Az n dimenziós egyenes definíciója című írásban.
Az S szakaszt meghatározó elsődleges feltételek a következők.:
1. A szakasz bejárása során minden pontját csak egyszer érintjük.
2. Az n pontból álló szakasznak n-2 olyan pontja van, aminek csak és kizárólag két szomszédja van. A két végpontnak csak egy szomszédja van.
Kiegészítő feltétel a szakasz görbeségének kizárására.:
3. Nincs olyan pont az S szakaszon kívüli, n dimenziós beágyazási környezetben, amely origója egy olyan tetszőleges sugarú körnek, amely két vagy több pontban érinti a szakaszt.
A fentiekből következik, hogy két pontból még nem lesz szakasz attól, hogy összekötjük őket, egy folytonos pontsorozat részének tekintve halmazukat. Ebben az esetben ugyanis a szakasznak csak végpontjai vannak, tehát nincs közbülső pontja. Így nem igaz rá a 2. feltétel, mert nincs olyan pontja, aminek csak és kizárólag két szomszédja van. A minimális hosszúságú szakasz hossza tehát három pontnyi. Három pont így már kiterjedést alkot: egy dimenziót, vagyis együttesük nem tekinthető 0D-s pontnak.
Érdekes ellentmondás viszont, hogy a három pontból álló minimálszakasz tényleges hossza valójában csak két pontnyi, mivel bármelyik végéről mérjük is, az első pontot mindig nullapontnak kell tekintenünk (lásd a számegyenest). Így tulajdonképpen igaza van azoknak, akik szerint a két pontból álló "szakasz" tényleges hossza csak egy pontnyi, mert ekkor az egyetlen pont hossza nulla pontnyi lesz. Minden attól függ, mit és honnan nézünk, mihez viszonyítunk a modellezés során. És ne feledjük: a pontoknak nincs tényleges térbeli kiterjedésük, tehát a hosszúság alatt itt mértékegység nélküli mértéket értünk minden esetben.
6. A MINIMÁLKÖR
A kör azon pontok halmaza a síkban, amik egy ponttól egyenlő távolságra vannak. A körnek van origója, sugara és körvonala (határoló széle). A sugár segítségével számolható ki a kerülete és területe. A kör kerülete, széle egy 1D-s zárt görbe, míg a területe, amit elfoglal a síkban egy 2D-s véges felület.
Vajon hány pontból kell minimálisan állnia a létező legkisebb kör kerületének (körvonalának) ahhoz, hogy már igaz legyen rá a kör definíciója? A téma előzményét részletesen lásd: Az n dimenziós kör definíciója című írásban.
Az origó pontja nem képezi részét a körvonalnak, miként a sugár sem. A kör kerületének tehát csak a következő feltételnek kell megfelelnie.: Egy dimenziós zárt görbe legyen. Ennek a minimális hossza, mint tudjuk legalább három pontnyi. Három pont hurokba kötve már ciklust (zárt görbét) alkot, de nem felel meg a körre vonatkozó összes további feltételnek.
A körrel kapcsolatban tudjuk, hogy az átmérővonalának hossza mindig kisebb, mint a kerület fele ( d<(d/2)xPi ). Három pontos körnél az átmérővonal azonos bármelyik két pont távolságával, mivel az csak a körvonalat alkotó pontok között húzható meg. Két pont már csak ezért sem alkothat kört (miként szakaszt sem). A körvonalat az átmérővonal két egyenlő hosszúságú részre (félkörre) osztja. Másként megfogalmazva: a körvonalon vannak egymással nem szomszédos pontok. A három pont hosszúságú körvonal nem osztható fel ily módon, ráadásul minden pontja szomszédos egymással. A négy pont hosszúságú körvonal viszont megfelel ezeknek a feltételeknek. Emiatt a legkisebb kerületi hosszúságú minimálkör négy pontból áll. A három pontos kört tehát nevezzük a továbbiakban protokörnek.
A négy pontos kör átmérője nulla, ezért nincs sugara. Ha a közepébe beteszünk egy pontot origónak, akkor az átmérője logikusan három pontnyi (két pont hosszú) lesz, ami már szakasznak számít, de ez nem növeli meg a kör tényleges átmérőjét fizikailag, mivel ebből csak egy pont esik a kör belsejébe, ami nem része a körvonalnak.
A négy pontos kör területe fizikailag kvázi nulla, logikailag viszont r^2xPi, ahol az r a két pont közötti nulla távolságot jelenti. Mivel a távolság fogalmába beletartoznak a végpontok is, elvileg a sugárnak két pontnyinak kellene lennie. Valójában azonban csak egy pontnyi, mert akármelyik irányból is mérjük (az origótól vagy a körvonaltól) a sugarat, a kiindulási pontot matematikailag mindig nullapontnak tekintjük. Tehát a sugár hossza egy pontnyi. A minimálkör területe ezért logikailag Pi. Tekinthető-e ez sík felületnek?
Ha a minimális kiterjedés három pontnyi az 1D-ben, akkor az összes többi magasabb dimenzióban is ennyi lesz. A legkisebb sík felületnek tehát három pontnyi hosszúnak és szélesnek kell lennie. Azt gondolnánk ez alapján, hogy a 3x3 pontnyi élhosszúságú négyzet lesz a minimálsík (9 pont), de ez így elhamarkodott következtetés. A dimenziószámot a vizsgált objektumra ráhelyezhető térkereszt egyeneseinek számával határozzuk meg. A két változós térkereszt minimális mérete ezért 5 pontnyi, mivel a két egyenesnek van egy közös metszéspontja. A minimálsíkon már ábrázolható a minimálkör 4 pontja. Törvényszerű tehát, hogy ennél kisebb folytonos és összefüggő síkfelület nem hozható létre.
7. A MINIMÁLGÖMB
A 3D-s térbe kiterjesztett kör a gömb, ami azon pontok halmaza a térben, amik egy ponttól egyenlő távolságra vannak. A gömbnek van origója, sugara, felszíne és térfogata. A gömb felszíne (területe) egy 2D-s zárt és véges felület, míg a térfogata egy 3D-s véges tér.
Vajon hány pontból kell minimálisan állnia a létező legkisebb gömb felületének ahhoz, hogy már igaz legyen rá a gömb definíciója? A téma előzményét részletesen lásd: Az n dimenziós kör definíciója című írásban.
Az origó pontja nem képezi részét a gömbfelszínnek, miként a sugár sem. A gömb felszínének tehát csak a következő feltételnek kell megfelelnie.: Két dimenziós zárt, görbült felület legyen. Ennek a minimális területe (minimálsík), mint tudjuk a minimálkörről szóló fejezetből, legalább öt pontnyi. Öt pont hurokba kötve már ciklust (zárt felületet) alkot, de nem felel meg a gömbre vonatkozó összes további feltételnek.
A gömbbel kapcsolatban tudjuk, hogy a felszínére három olyan körvonal rajzolható, melyek egymást merőlegesen metszik. Így mindegyik körvonal négy egyenlő hosszúságú részre (negyedkörre) oszlik. A metszéspontokat egyenesekkel összekötve három átmérővonalat kapunk, melyek az origóban metszik egymást és szintén mind merőlegesek egymásra. Logikusnak tűnik tehát, hogy a minimálgömb átmérővonalai megfelelnek egy minimális méretű térkeresztnek, ami 7 pontból áll. Ez a minimáltér, amiben ábrázolható a minimálgömb 6 pontja. Ennél kisebb folytonos és összefüggő térfogat nem hozható létre. Az öt pontból álló gömböt éppen ezért nevezzük a továbbiakban protogömbnek.
A hat pontos gömb átmérője nulla, ezért nincs sugara. Ha a közepébe beteszünk egy pontot origónak, akkor az átmérője logikusan három pontnyi lesz, de ez nem növeli meg a gömb tényleges átmérőjét fizikailag, mivel ebből csak egy pont esik a gömb belsejébe, ami nem része a gömbfelületnek.
A hat pontos gömb felszíne fizikailag nulla, logikailag viszont 4xr^2xPi, ahol az r a két pont közötti nulla távolságot (egy pontnyit) jelenti, miként a minimálkörnél. A gömb felülete ezért logikailag 4xPi. A térfogata fizikailag nulla, logikailag viszont (4xr^3xPi)/3, ami (4xPi)/3-ra egyszerűsíthető.
Időfizikai kiegészítés: A fotinót leíró modelljeinkben a téridőben született időhurkok, energiakvantumok olyan fénykvantumok, amikben hét időforrás másolódik körbe egy nyolcas szimmetriában. Ez geometriailag a 3D-ben egy kockával ábrázolható, amiben ha egyenesekkel összekötjük a csúcspontokat abban a sorrendben, ahogyan az időhurokban felvillannak egymás számára, akkor szintén egy 4xPi hosszúságú szakaszt kapunk. A fotinó forrásai tehát gyakorlatilag egy minimális gömbfelületen mozogva fordulnak körbe a téridőben ciklusonként. A minimálfelületre rajzolt bejárási útvonal teljesen lefedi a felületet, ezért fizikailag a hossz és a terület egyenlőnek mutatkozik, bár makroszinten két különböző dologról van szó (a hossz 1D-s, a terület 2D-s). A minimálgömb térfogata pedig az a minimáltér, ami egy három egyenesből álló térkeresztnek felel meg. Ennek végpontjait egyenesekkel összekötve egy oktaédert kapunk, ami a térkvantum (szerinó) geometriai ábrázolásának felel meg.
8. A MINIMÁLHIPERGÖMB
A 4D-s túltérbe (hipertérbe) kiterjesztett kör a hipergömb, ami azon pontok halmaza a túltérben, amik egy ponttól egyenlő távolságra vannak. A hipergömbnek van origója, sugara, térfogata és túltérfogata. A hipergömb térfogata egy 3D-s zárt és véges térfogat, míg a túltérfogata egy 4D-s véges túltér.
Vajon hány pontból kell minimálisan állnia a létező legkisebb hipergömb térfogatának ahhoz, hogy már igaz legyen rá a hipergömb definíciója? A téma előzményét részletesen lásd: Az n dimenziós kör definíciója című írásban.
Az origó pontja nem képezi részét a hipergömbtérfogatnak, miként a sugár sem. A hipergömb térfogatának tehát csak a következő feltételnek kell megfelelnie.: Három dimenziós zárt, görbült térfogat legyen. Ennek a minimális térfogata (minimáltér), mint tudjuk a minimálkörről szóló fejezetből, legalább hét pontnyi. Hét pont hurokba kötve már ciklust (zárt térfogatot) alkot, de nem felel meg a hipergömbre vonatkozó összes további feltételnek.
A hipergömbbel kapcsolatban valószínűsíthetjük az eddigiek alapján, hogy a térfogatára három olyan felszín rajzolható, melyek egymást merőlegesen metszik. Így mindegyik felszín négy egyenlő területű részre (negyedgömbre) oszlik. A metszési síkokat a hipergömbön belül síkokkal összekötve három átmérősíkot kapunk, melyek az origóban metszik egymást és szintén mind merőlegesek egymásra. Logikusnak tűnik tehát, hogy a minimálhipergömb átmérősíkjai megfelelnek egy minimális méretű térkeresztnek, ami 9 pontból áll. Ez a minimáltúltér, amiben ábrázolható a minimálhipergömb 8 pontja. Ennél kisebb folytonos és összefüggő túltérfogat nem hozható létre. A hét pontból álló hipergömböt éppen ezért nevezzük a továbbiakban protohipergömbnek.
A nyolc pontos hipergömb átmérője nulla, ezért nincs sugara. Ha a közepébe beteszünk egy pontot origónak, akkor az átmérője logikusan három pontnyi lesz, de ez nem növeli meg a hipergömb tényleges átmérőjét fizikailag, mivel ebből csak egy pont esik a hipergömb belsejébe, ami nem része a hipergömbtérfogatnak.
A nyolc pontos hipergömb térfogata és túltérfogata fizikailag nulla, logikailag viszont egyelőre nem tudjuk mennyi lehet számszerűen. A jövő matematikusaira vár a feladat, hogy meghatározzák a hipergömb térfogatának és túltérfogatának kiszámítási képletét.
9. ÖSSZEFOGLALÁS
Foglaljuk össze az eddigeket a minimális kiterjedésekről.:
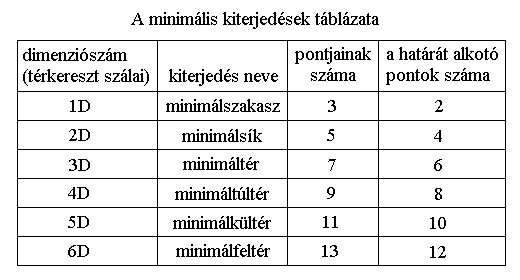
Az 1D-s minimálszakasz 3 pontból áll, rajta a minimállétező helye 2 pontnyi.
A 2D-s minimálsík 5 pontból áll, rajta a minimálkör kerülete 4 pontnyi.
A 3D-s minimáltér 7 pontból áll, rajta a minimálgömb felszíne 6 pontnyi.
A 4D-s minimáltúltér 9 pontból áll, rajta a minimálhipergömb térfogata 8 pontnyi.
Az 5D-s minimálkültér 11 pontból áll, rajta a minimálextragömb túltérfogata 10 pontnyi.
A 6D-s minimálfeltér 13 pontból áll, rajta a minimálultragömb kültérfogata 12 pontnyi.
Képletszerűen felírva: P = (nx2)+1 , ahol P az alkotó pontok száma, n a dimenziók száma.
Ebből következik, hogy:
Az 1D-s minimálszakasz azonos egy tömör minimálkörszakasszal.
A 2D-s minimálsík azonos egy tömör minimálkörrel.
A 3D-s minimáltér azonos egy tömör minimálgömbbel.
A 4D-s minimáltúltér azonos egy tömör minimálhipergömbbel.
Az 5D-s minimálkültér azonos egy tömör minimálextragömbbel.
A 6D-s minimálfeltér azonos egy tömör minimálultragömbbel.
10. AZ IDŐPONTOK
Most vizsgáljuk meg a három pontból álló létezést abból a szemszögből, hogy az egyes pontok milyen időpillanatokat reprezentálnak rajta.:
1. Mindhárom pont egyidejű: AAA. Ekkor a pontok az egymáshoz viszonyított helyzetükben, realizációs távolságukban különböznek. Mivel a három pontos létezésnek nincs beágyazási környezete, kiterjedéssel bíró tere, amiben elhelyezhetnénk a további vizsgálatokhoz, azt kell mondanunk, hogy a három pontnak azonos a forgása (iránya, sebessége). Ez egyenértékű azzal, hogy nem forognak. Ha nincs különbség, nem értelmezhető a mozgás. Az időbeli és térbeli távolságuk ezért gyakorlatilag nulla. Az AAA pontok így egy időtlen és teretlen, statikus minimálszakaszt vagy protokört alkotnak, aminek tulajdonságai nem változnak meg attól, hogy bővítjük a rendszert további A pontokkal. Ebből a lehetőségből tehát nem lehet tovább lépni sehová. Ilyen a klasszikus matematika statikus, életlen és élettelen egyenese.
2. Mindhárom pont eltérő idejű: ABC. Ekkor a pontok az egymáshoz viszonyított időbeli megnyilvánulásukban, időtartamukban különböznek. Ez megfeleltethető az eltérő forgási irányoknak és forgási sebességnek, amik a következő lehetőségeket kínálják.: A forgásirány lehet azonos: BBB vagy JJJ, miközben a forgási sebességek eltérőek: 123. A forgásirány lehet eltérő: BBJ vagy BJJ, miközben a forgási sebességek eltérőek: 123. A forgásirány: BBJ vagy BJJ, miközben az azonos forgásirányúak sebessége eltérő: 122 vagy 121. Ha a forgásirány és a forgási sebesség is azonos lenne két pont esetében, akkor már nem lenne a három pont eltérő idejű: ezzel a következő pontban foglalkozunk.
Az ABC pontok alkothatnak minimálszakaszt és protokört is, melyeken irányultság figyelhető meg a különbözőségek miatt. A minimálszakasz így viselkedhet minimálvektornyílként, míg a protokörön kapunk egy körbejárási irányt. Ez már egy mozgó és változásra képes rendszer, amit további pontokkal (DEF...) bővítve új szerkezeteket kaphatunk. Ilyenek az új időmatematika dinamikus, éles és élő egyenesei és több változós kiteljesedésű objektumai.
A protokörön körbejáró szemlélő útvonala tehát: ABCABC... lesz. Fordított irányban haladva (az időben visszafelé) CBACBA... Látható, hogy a két sorozatból a három triplet mindegyike kiemelhető: ABC, BCA, CAB, CBA, BAC, ACB, vagyis az összes sorrend, mint lehetőség (a teljesség) megbújik benne. Hogy mit emelünk ki ebből a magunk számára, csak a szemléletünktől függ.
3. Két pont egyidejű a háromból: AAB vagy ABB. Az egyidejűség azt jelenti, hogy azonos a forgási irányuk és sebességük. Ez a két előző modell keveredése, ami logikailag azonos két ponttal: AB. Ha tovább bővítjük és megengedjük, hogy a rendszerben több egyidejű pont legyen (tetszőleges számban), akkor ezzel megjelenik a holtpont és a halál fogalma. Az azonos pontok nem adnak új információt (minőséget) a rendszerhez, mivel egymás egyenértékű másolatainak tekinthetők. Mennyiségi növekedést viszont okoznak, és statikus, halott zónákat hoznak létre az egészen belül.
A dinamikus, mozgó részek így szeparálódni kezdenek egymástól, vagyis több, egymástól független és kvázi önálló rendszer fogja alkotni a teljes ponthalmazt. Mi ilyennek tapasztaljuk meg a teremtést: vannak benne élő és élettelen dolgok, illetve minden élő dolog mérete és mozgása korlátozott a térben és időben egyaránt.
11. FÉL DIMENZIÓK
Felmerül a kérdés, hogy a három pontból álló protokör és magasabb dimenziószámú rokonai (protogömb, protohipergömb, stb.) vajon hány dimenziósak? És mi a helyzet az olyan objektumokkal, mint a tetraéder formációban elhelyezett négy pont vagy a hipertetraéder formációban elhelyezett öt pont? Rengeteg féle olyan egzotikus objektumot lehet alkotni, amik dimenziószáma kétséges és őket is kezelnünk kellene valahogy.
Szemléljük rugalmasan ezeket a speciális objektumokat. A körszakasz 1D-s, aminek a két végpontja egy helyen van. Ez szemléletesen ábrázolható 2D-ben körvonalként, ahogy a kvázi végtelen egyenes is valójában egy kör a létezésben. A protokör tehát 1D-s, de ábrázolható 2D-ben anélkül, hogy ténylegesen 2D-s lenne (mivel nem fedi le a minimálsíkot). Azt is mondhatjuk tehát, hogy a protokör átmenetet képez a dimenziószintek között: másfél dimenziós.
Ennek megfelelően a protogömb két és fél dimenziós lesz, a protohipergömb pedig három és fél dimenziós. A fél dimenzió nem valódi kiterjedés, hanem praktikus leképzés eredménye, amivel a modellünk a speciális lehetőségekre is alkalmazhatóvá válik.
A rugalmas szemléletmód megengedi, hogy a térszál használatával kétféle módon tüntessük el a fél dimenziókat, amennyiben meg akarunk szabadulni tőlük. Egyrészt ha megengedjük, hogy a szomszédos pontok távolsága különböző legyen, akkor a protokör pontjai kisimíthatók egy térszál mentén anélkül, hogy a körvonal elszakadna. Ebben az esetben a fél dimenziókat mindig lefelé kerekíthetjük. Másrészt ha a szomszédos pontokat egyenesekkel (térszálakkal) kötjük össze, majd a pontok közé további n darab pontot zsúfolunk be az egyenesekre, akkor ezzel megnövelhetjük az objektum méretét akkorára, hogy rá lehessen illeszteni egy térkeresztet. Ebben az esetben a fél dimenziókat mindig felfelé kerekíthetjük.
Miután az időmatematika geometriai alapjait lefektettük, a nagyobb kiterjedésű objektumok tulajdonságainak vizsgálata olyan eredményekre vezetett, amik megalapozták az időmatematika topológiáját is. Ezeket az Időtopológia című publikációban részletezzük.
Készült: 2003.01.21. - 2006.07.17.
Következő írás
Vissza a tartalomhoz