"Egy
szóló felület szelése szálszerűen szaladó széleket szül."
1. BEVEZETÉS
A topológia a matematika azon ága, mely a folytonosság általános törvényszerűségeivel foglalkozik. Ilyenek a halmazelemek ama tulajdonságai, melyek a halmaz deformációja során változatlanok maradnak. Megengedett deformációnak számít a nyújtás, összenyomás és torzítás, elterjedtebb nevén a gyurmázás, mert ezek a műveletek nem változtatják meg a halmazok topológiai tulajdonságait. Az időmatematikában az időtopológia hasonló, de nem azonos szerepet tölt be, mivel a dinamizmus érdekében további műveletek is megengedettek: a vágás és ragasztás, lásd a szalagológiai kutatási anyagokat a 2004-es év anyagai között. Emellett a gyurmázás csak bizonyos korlátok között végezhető, lásd később.
Ebben az írásunkban a topológiai halmazok alkotóinak tulajdonságaival és a rajtuk végezhető egyszerűbb műveletek következményeivel foglalkozunk részletesen. A megértéshez szükséges ismerni a korábbi időfizikai és időgeometriai publikációkat is. Ezekre nem utalunk külön a cikkben, feltételezve, hogy az Olvasó már megismerkedett velük.
2. AZ ALKOTÓK
Az n dimenziós véges és összefüggő (folytonos) objektumok határpontjai mindig n-1 dimenziós kiterjedést alkotnak. Az ennél alacsonyabb dimenziószámú alkotók nem topológiai alkotók, mert gyurmázással eltüntethetők. Tehát egy objektumnak topológiai szemmel nézve kétféle alkotója van: egy n dimenziós belseje és egy vagy több n-1 dimenziós határolófelülete. Geometriailag azonban bármilyen n-nél kisebb alkotói lehetnek (tetszőleges mennyiségben) az objektumnak. Ennek alapján a következő szabályok alkothatók n dimenzióban.:
Az 1D-s szakasznak vannak csúcspontjai és éle. Geometriailag és topológiailag egyaránt.
A 2D-s síkidomnak vannak élei és felülete. Geometriailag lehetnek csúcsai, topológiailag nem.
A 3D-s testnek vannak felületei és térfogata. Geometriailag lehetnek csúcsai és élei, topológiailag nem.
A 4D-s hipertestnek vannak térfogatai és túltérfogata. Geometriailag lehetnek csúcsai, élei és felületei, topológiailag nem.
Az 5D-s extratestnek vannak túltérfogatai és kültérfogata. Geometriailag lehetnek csúcsai, élei, felületei és térfogatai, topológiailag nem.
A 6D-s ultratestnek vannak kültérfogatai és feltérfogata. Geometriailag lehetnek csúcsai, élei, felületei, térfogatai és túltérfogatai, topológiailag nem.

Speciális csoportot alkotnak azok az n dimenziós véges objektumok, melyek belseje nem összefüggő, csak a határolófelülete. Ezeknek topológiailag több nD-s belseje és több n-1D-s határolója is lehet. Ilyen például a lemniszkáta alakú síklap, aminek két önálló belseje van, mégis egyetlen, összefüggő objektumnak tekinthető az egy pontban érintkező határológörbe miatt. Az ilyen objektumokat a szemléletmódunktól függően tekinthetjük egymástól független (önálló), de a határolóikkal érintkező, azaz szomszédos objektumoknak is.
3. AZ OLDALAK SZÁMA
A klasszikus topológiában egy oldalú az a felület, amelyen mozogva bármely pont bármely más ponttal összeköthető egy folytonos vonallal anélkül, hogy a vonal elszakadna a felülettől, áthaladna a felület szélét alkotó határpontokon vagy átlyukasztaná a felületet. Ez a vonal (a továbbiakban: V) lehet egyenes vagy görbe. Tehát V minden pontjának rá kell feküdnie a felületre, de a határpontokkal nem kerülhet fedésbe (de szomszédos lehet velük). Amely felületen van olyan pont, amely ezen a módon nem köthető össze más pontokkal, az két oldalú.
Az időtopológiában a felület definíciója némileg eltér ettől. Ha megvizsgálunk egy egy pontnyi "vastagságú" síklapot abból a szempontból, hogy hány oldala van, azt látjuk, hogy egy oldalú. A felületén haladó V ugyanis minden pontját képes elérni anélkül, hogy át kellene haladnia a határpontokon. Egy két pontnyi "vastagságú" síklap esetén ugyanez a helyzet, mert a felső pontokról bármikor áttérhet a V az alsó pontokra anélkül, hogy akár csak egyetlen pontnyi szakaszon is elhagyná a felületet. Az áttérés során ráadásul V nem lyukasztja át a felületet, mert a lyukasztás egyenértékű a felületet alkotó ponthalmaz elhagyásával. Ennek megfelelően az egy és két pontnyi "vastagságú", tehát 2D-s felületeken a két oldalúság nem értelmezhető sem lokálisan, sem globálisan.
A három pontnyi vastagságú felület esetében már elmondhatjuk, hogy bármely két felületi pont között mindig van egy közbülső, belső pont, ami nem a felület része. Így ezt már át lehet lyukasztani, tehát a felület lokálisan mindig két oldalú lesz. Globálisan azonban nem ilyen egyszerű a helyzet. A három pontnyi vastagságú felület széle, határológörbéje ugyanis ha három pont szélességű, akkor már nem élnek, hanem síkfelületnek számít maga is. Vagyis az objektum valójában 3D-s, és a szélét alkotó felület két élvonala gyurmázással eltüntethető, mivel 1D-snek minősül. Így topológiailag az objektum egyenértékű a tömör gömbbel. Ha a három pontnyi vastagságú felület szélét körben összenyomjuk, hogy két pontnyi vagy egy pontnyi vastagságú legyen, akkor ismét abban a helyzetben vagyunk, hogy a szél pontjai átjárhatók V számára, tehát az objektum egy oldalú.
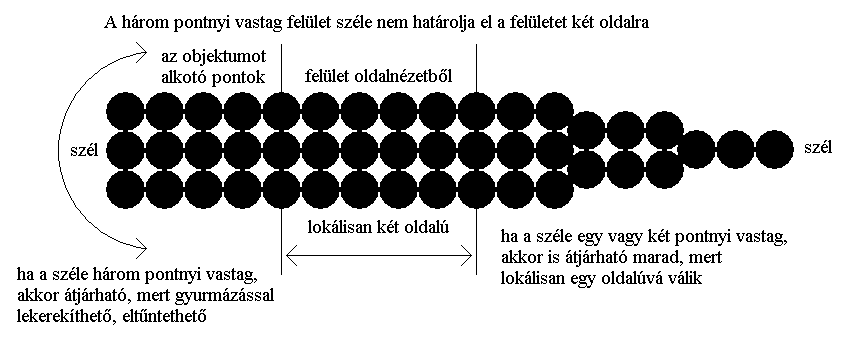
Ha a három pontnyi vastagságú felületet 3D-ben meghajlítjuk és gömbfelszínt hozunk létre belőle, akkor azzal eltüntetjük a szélét és ezáltal a felület globálisan is két oldalúvá válik, mert a külső oldaláról nem képes a V átjutni a belső oldalára. Ez a transzformáció lehetővé teszi, hogy egy 3D-s testnek n számú oldala legyen, ahogy a 2D-s síklapoknak is n számú határolóéle lehet azáltal, hogy véges méretű lyukakat hozunk létre rajtuk. Egy három pontnyi vastagságú körvonalnak például két széle, határolóéle van: egy külső és egy belső. Ha tehát n darab üreget hozunk létre a 3D-s testben, melyeket minimálisan három pontnyi fal választ el egymástól, akkor az objektumnak n+1 oldala lesz összesen. Ezt hívjuk sokoldalúságnak.
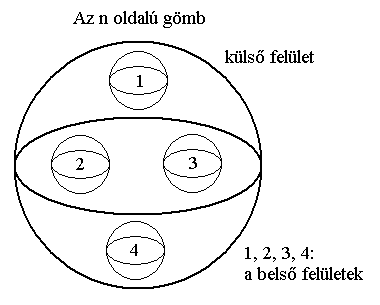
Ezek a szabályok tetszőleges magasabb dimenziószámú objektumok esetén is érvényesek lesznek. Példa: A határolótérfogat 4D-ben deformálható gyurmázással, de nem tüntethető el. 5D-ben viszont gyurmázással és ragasztással eltüntethető, ami eggyel megnöveli az objektum globális dimenziószámát. Összefoglalva tehát a következő szabályszerűségre jutunk a határolófelületek számát illetően.:
A 0D-s objektumoknak csak egy pontulata lehet, az 1D-seknek tetszőleges számú.
Az 1D-s objektumoknak csak egy éle lehet, a 2D-seknek tetszőleges számú.
A 2D-s objektumoknak csak egy felszíne lehet, a 3D-seknek tetszőleges számú.
A 3D-s objektumoknak csak egy térfogata lehet, a 4D-seknek tetszőleges számú.
A 4D-s objektumoknak csak egy túltérfogata lehet, az 5D-seknek tetszőleges számú.
Az 5D-s objektumoknak csak egy kültérfogata lehet, a 6D-seknek tetszőleges számú.
A 6D-s objektumoknak csak egy feltérfogata lehet, a 7D-seknek tetszőleges számú.
4. A KÉT OLDALÚ MINIMÁLGÖMB
Ha a legkisebb 3D-s kiterjedés 7 pontnyi, ami megfelel egy tömör (és egyoldalú) minimálgömbnek, akkor ennek alapján előállítható az a legkisebb üres gömb, amelynek két oldala van. Csak a minimálgömb 6 felületi pontját kell három pontnyi vastagságúra kibővíteni, vagyis 18 pontra növelni.
De miért van szükség egy efféle két oldalú minimálgömbre? Azért, mert a topológiában minden normális, véges sugarú üres gömbnek kétoldalú a felszíne. Van egy külső és egy belső oldala. Ha egy gömb nem két oldalú, akkor vagy tömör vagy nem nevezhető gömbnek, hanem topológiailag egy osztályba tartozik a tórusszal (Manduval).
A kétoldalú minimálgömb tehát gyakorlatilag megfelel három koncentrikusan egymásba helyezett minimáloktaédernek. Ennek a külső és belső felszíne egyaránt hat pontnyi, így a gömbfelületet továbbra is eszményien vékonynak kell tekintenünk. Az origó és a felület között meghatározható külső és belső sugár éppen ezért nem választható el egymástól, vagyis fizikailag mindkettő ugyanannyi: nulla. Külső szemlélő számára azonban úgy tűnik, hogy a gömb belső átmérője 2 pontnyi (origó nélkül), a külső viszont 6 pontnyi. Mindez csak attól függ, mit és honnan számolunk a mérés során. Ezzel a témával a korábbi írásokban már részletesen foglalkoztunk.
Időfizikai kiegészítés a 18 pontból álló minimálgömbhöz: A triász szerinóról tudjuk, hogy az időforrásai (5 jelenpont) a térszorzás miatt egy négy dimenziós pályagörbe mentén körbemásolódva három, egymással párhuzamosan és felváltva létező, felvillanó térhatost keltenek ciklusonként. Ez a folyamat 16 forráshelyen történik és 18 felvillanást eredményez sorban (plusz a királylány forrás 3x3 felvillanása minden térhatos belsejében). Így működik a triász univerzum.
5. A SZOMSZÉDOSSÁG
A topológiában az objektumokat alkotó pontok közvetlenül egymás mellett helyezkednek el, vagyis szomszédosak. Ezt nem befolyásolja a gyurmázás, mivel a pontok távolsága geometriai tulajdonság. A topológiai kiterjedések tehát folytonos pontsokaságnak minősülnek, ahol nincs jelentősége a pontok sűrűségének az objektumon belül. Most vizsgáljuk meg az ebből fakadó következményeket.
Felmerül a kérdés, hogy ha két nulla felületű pont szomszédos, és nulla felületen érintkeznek egymással, akkor elvileg teljesen lefedik, azaz beburkolják egymást vagy nem? Ha beburkolnák egymást, akkor egy pontnak csak egy (közvetlen) szomszédja lehetne összesen. Együtt Bindut alkotnának, amiből nem lehetne szálat készíteni további pontok hozzáadásával és itt meg is akadna a folytonos pontsokaságok bővítése, kiterjesztése. Mivel ez a kérdés a nullából fakadó ellentmondások miatt nem tisztázható egyértelműen, azt kell mondanunk (praktikus megoldásként), hogy nincs korlátja az egymással szomszédos pontok számának. Többek között ennek is köszönhető, hogy nincs matematikai korlátja a dimenziók számának, valamint, hogy a pontsokaságok folytonosnak tekinthetők a kiterjedésükben.
Ennek alapján a szomszédosságot a következőképpen kell definiálnunk.: Két pont akkor szomszédos, ha a távolságuk nulla és így nem lehet közéjük egyetlen pontot sem elhelyezni. Tehát ha két kvázi (logikailag) nulla távolságra lévő pont között van még legalább egy harmadik pont, akkor azok a pontok nem szomszédosak és a távolságuk nagyobb a tényleges (fizikai) nullánál. Ebből következik, hogy a 2 pont vastag felület 2D-s, mert nincs tényleges vastagsága a síkra merőlegesen, míg a 3 pont vastag felület már 3D-s, lásd a három pont tételt.
Elméletileg tehát egy P0 pont köré végtelen számú másik pontot helyezhetünk el úgy, hogy mind a közvetlen szomszédja legyen, vagyis a pontulatukkal érintkezzenek. Felmerül a kérdés, hogy ha P0-nak szomszédja P1 és P2, akkor vajon P1 és P2 is szomszédja-e egymásnak vagy nem? Ha a szomszédos pontokat körben ábrázoljuk P0 körül, akkor logikus, hogy két szomszédos pont esetében mindenki szomszédja mindenkinek egy protokörön. Három szomszéd esetén a négy pont akkor szomszédja egymásnak, ha egy tetraéder csúcsain helyezkednek el, öt pontnál pedig egy hipertetraéder csúcsain. A pontok elhelyezkedése egy teljes gráffal ábrázolható, ami (véges hosszúságú élek esetén) mindig n-1 dimenziós. Mivel azonban a pontok szomszédosak, az őket összekötő éleknek nincs tényleges hossza, ezért a ponthalmaz egyik irányban sem éri el a három pontnyi hosszúságot, tehát n pont esetén is megmarad effektíve 0D-snek.
Ennek alapján azt gondolnánk, hogy minden folytonos pontsokaság lokálisan 0D-s, de ez hibás következtetés, mert a tetszőlegesen kicsiny kiterjedést nem lehet egyetlen pontra korlátozni a dimenziószámának sérülése (elvesztése) nélkül. Így a "tetszőlegesen kicsiny" kiterjedés fogalmát a lokális dimenziószám és más topológiai tulajdonságok meghatározásához módosítanunk kell "minimális méretű" kiterjedésre.
6. AZ ALKOTÓK TÉRDIMENZIÓSZÁMA
A geometriai objektumok alkotóinak dimenziószámát egy térkereszt ráillesztésével határozhatjuk meg. Egy objektum annyi térdimenziós, ahány egyenese van a pontjaira illeszthető térkeresztnek. Ugyanezen módon meghatározható a topológiai objektumok alkotóinak lokális és globális dimenziószáma is.
Egy 1D-s objektum (szakasz) végpontja lokálisan 0D-s, de globálisan mindenképpen 1D-s. Az éle viszont lokálisan és globálisan is 1D-s, mert az alkotó pontjaira egy X térkereszt (azaz egy egyenes) illeszhető csak rá. Az Y egyenes mindenképpen kilóg az élből, akár egy pontnyi, akár két pontnyi széles.
Egy 2D-s objektum (síklap) széle lokálisan 1D-s, de globálisan mindenképpen 2D-s. A felülete viszont lokálisan és globálisan is 2D-s, mert az alkotó pontjaira egy XY térkereszt illeszthető rá. A Z egyenes mindenképpen kilóg a felületből, akár egy pontnyi, akár két pontnyi vastag.
Egy 3D-s objektum (gömb) felülete lokálisan 2D-s, de globálisan mindenképpen 3D-s. A térfogata viszont lokálisan és globálisan is 3D-s, mert az alkotó pontjaira egy XYZ térkereszt illeszthető rá. A V egyenes mindenképpen kilóg a térfogatból, akár egy pontnyi, akár két pontnyi vastag.
Egy 4D-s objektum (hipergömb) térfogata lokálisan 3D-s, de globálisan mindenképpen 4D-s. A túltérfogata viszont lokálisan és globálisan is 4D-s, mert az alkotó pontjaira egy XYZV térkereszt illeszthető rá. Az U egyenes mindenképpen kilóg a túltérfogatból, akár egy pontnyi, akár két pontnyi vastag.
Egy 5D-s objektum (extragömb) túltérfogata lokálisan 4D-s, de globálisan mindenképpen 5D-s. A kültérfogata viszont lokálisan és globálisan is 5D-s, mert az alkotó pontjaira egy XYZVU térkereszt illeszthető rá. A T egyenes mindenképpen kilóg a kültérfogatból, akár egy pontnyi, akár két pontnyi vastag.
Egy 6D-s objektum (ultragömb) kültérfogata lokálisan 5D-s, de globálisan mindenképpen 6D-s. A feltérfogata viszont lokálisan és globálisan is 6D-s, mert az alkotó pontjaira egy XYZVUT térkereszt illeszthető rá. Az S egyenes kilóg a feltérfogatból, akár egy pontnyi, akár két pontnyi vastag.
Amint az látható, itt ugyanazon eredményekre jutottunk, mint amiről a korábbi fejezetekben már volt szó. De a teljesség érdekében most vizsgáljuk meg a kérdést fordítva, hogy egy P pont az n dimenziós objektum mely alkotójához tartozik annak alapján, hogy a ráillesztett térkereszt (metszéspontjában P-vel) egyenesei hány szomszédos pontjára illeszkednek maximálisan.
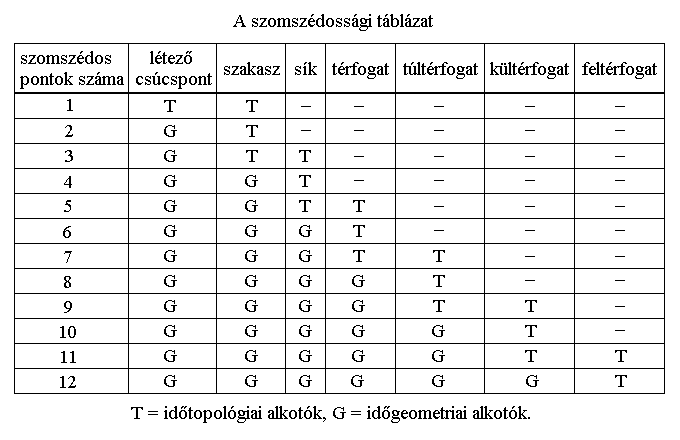
Ha a szomszédos pontok száma:
1, akkor P lehet egy 1 pont széles szakasz végpontja vagy a 2 pontból álló létező egyik (belső) pontja.
2, akkor P lehet egy 1 pont széles szakasz belső pontja.
3, akkor P lehet egy 1 pont vastag síkfelület szélének pontja vagy egy 2 pont vastag szakasz belső pontja.
4, akkor P lehet egy 1 pont vastag síkfelület belső pontja.
5, akkor P lehet egy 1 pont vastag térfogat felszíni pontja vagy egy 2 pont vastag síkfelület belső pontja.
6, akkor P lehet egy 1 pont vastag térfogat belső pontja.
7, akkor P lehet egy 1 pont vastag túltérfogat térfogati pontja vagy egy 2 pont vastag térfogat belső pontja.
8, akkor P lehet egy 1 pont vastag túltérfogat belső pontja.
9, akkor P lehet egy 1 pont vastag kültérfogat túltérfogati pontja vagy egy 2 pont vastag túltérfogat belső pontja.
10, akkor P lehet egy 1 pont vastag kültérfogat belső pontja.
11, akkor P lehet egy 1 pont vastag feltérfogat kültérfogati pontja vagy egy 2 pont vastag kültérfogat belső pontja.
12, akkor P lehet egy 1 pont vastag feltérfogat belső pontja.
Geometriailag P (n szomszédos pont esetén) minden alacsonyabb dimenziószámú alkotónak része lehet, mint tudjuk. A gyakorlatban ez a következőket jelenti.
Ha a szomszédos pontok száma:
1, akkor P lehet egy 1 pont széles szakasz végpontja vagy a 2 pontból álló létező egyik (belső) pontja.
2, akkor P lehet egy 1 pont széles szakasz belső pontja vagy egy 2D-s síkidom csúcspontja.
3, akkor P lehet egy 1 pont vastag síkfelület szélének pontja vagy egy 2 pont vastag szakasz belső pontja vagy egy 3D-s test csúcspontja.
4, akkor P lehet egy 1 pont vastag síkfelület belső pontja vagy egy 3D-s test élvonali pontja vagy egy 4D-s hipertest csúcspontja.
5, akkor P lehet egy 1 pont vastag térfogat felszíni pontja vagy egy 2 pont vastag síkfelület belső pontja vagy egy 4D-s hipertest élvonali pontja vagy egy 5D-s extratest csúcspontja.
6, akkor P lehet egy 1 pont vastag térfogat belső pontja vagy egy 4D-s hipertest felületi pontja vagy egy 5D-s extratest élvonali pontja vagy egy 6D-s ultratest csúcspontja.
7, akkor P lehet egy 1 pont vastag túltérfogat térfogati pontja vagy egy 2 pont vastag térfogat belső pontja vagy egy 5D-s extratest felületi pontja vagy egy 6D-s ultratest élvonali pontja vagy egy 7D-s test csúcspontja.
8, akkor P lehet egy 1 pont vastag túltérfogat belső pontja vagy egy 5D-s extratest térfogati pontja vagy egy 6D-s ultratest felületi pontja vagy egy 7D-s test élvonali pontja vagy egy 8D-s test csúcspontja.
9, akkor P lehet egy 1 pont vastag kültérfogat túltérfogati pontja vagy egy 2 pont vastag túltérfogat belső pontja vagy egy 6D-s ultratest térfogati pontja vagy egy 7D-s test felületi pontja vagy egy 8D-s test élvonali pontja vagy egy 9D-s test csúcspontja.
10, akkor P lehet egy 1 pont vastag kültérfogat belső pontja vagy egy 6D-s ultratest túltérfogati pontja vagy egy 7D-s test térfogati pontja vagy egy 8D-s test felületi pontja vagy egy 9D-s test élvonali pontja vagy egy 10D-s test csúcspontja.
11, akkor P lehet egy 1 pont vastag feltérfogat kültérfogati pontja vagy egy 2 pont vastag kültérfogat belső pontja vagy egy 7D-s test túltérfogati pontja vagy egy 8D-s test térfogati pontja vagy egy 9D-s test felületi pontja vagy egy 10D-s test élvonali pontja vagy egy 11D-s test csúcspontja.
12, akkor P lehet egy 1 pont vastag feltérfogat belső pontja vagy egy 7D-s test kültérfogati pontja vagy egy 8D-s test túltérfogati pontja vagy egy 9D-s test térfogati pontja vagy egy 10D-s test felületi pontja vagy egy 11D-s test élvonali pontja vagy egy 12D-s test csúcspontja.
7. MEGENGEDETT ÉS TILTOTT MŰVELETEK
A topológiában a szemléletesség érdekében megengedett műveletnek számít az objektumokon végzett nyújtás, zsugorítás és hajlítás, azaz a gyurmázás. Ennek során persze elvesznek a geometriai tulajdonságok, elsősorban a térbeli alakzat, de az objektum tartama és globális dimenziószáma, valamint az alkotó pontjainak mennyisége (darabszáma) nem változik meg.
Mindez azt jelenti, hogy például egy 3D-s alakzat nem nyomható össze gyurmázással 3 pontnál vékonyabbra sem lokálisan, sem globálisan. A pontok mennyiségének rögzítettsége pedig azt jelenti, hogy az alakzat a gyurmázás során nem válhat kisebbé vagy nagyobbá, tehát nem csökkenhet vagy nőhet a pontjainak száma. A dimenziószám és a pontok mennyisége így együtt adja a tartamot, ami minden véges alakzat lényegi tulajdonsága. Ezek adják az objektumok elsődleges információ tartalmát. Ha ezek közül valamelyiket megváltoztatjuk, akkor az objektum topológiai besorolása is megváltozik. Az objektumok másodlagos információ tartalma ennek megfelelően az alkotó pontjaik egymáshoz viszonyított helyzetében, alakzatában van, ami a gyurmázás során megváltozik.
Ha a dimenziószám gyurmázással megváltoztatható lenne, akkor elvileg minden 3D-s objektum simán kilapítható lenne egy egy pont vastag (2D-s) síkká, majd tovább lapítva egy egy pont vékony (1D-s) egyenessé, azonos pontmennyiség mellett. Így viszont a topológiai tulajdonságok is eltűnnek (értelmetlenné válnak), mert akkor minden dolgot egy szálra lehet redukálni. Ha ezt mégis megengedjük, akkor kapjuk az időszál univerzumot (az időfizikában), ami minden létező pontot a teremtésben összekapcsol a keltő pontjával (felettes létezőjével) egészen az okforrásokig visszamenően. Ebben az esetben viszont minden egyedi méretű (n darab pontból álló) objektum egyedi hosszúságú szállá redukálható. Ekkor kizárólag a pontok száma adja a szál információ tartalmát.
Ha megengedjük, hogy csak a pontok mennyisége legyen megváltoztatható, a dimenziószám pedig nem, akkor minden nD-s objektum összenyomható, összezsugorítható lenne egy nD-s minimálkiterjedéssé. Ez a dimenziószámának megfelelő térkeresztet még ráilleszthetővé teszi. Másrészt minden nD-s véges objektum felfújható, kitágítható lenne egy kvázi végtelen, határtalan nD-s kiterjedéssé, amitől elveszítené a határát, s vele geometriai és topológiai jellemzőit egyaránt.
Ha mindkét tulajdonság megváltoztatható, akkor az összes véges objektumot össze lehetne nyomni egy 0D-s ponttá, illetve ki lehetne tágítani egy kvázi végtelen, nD-s határtalansággá (minden létezővé). Ezek közös tulajdonsága, hogy mindkettő jellegtelen: semmi és minden egyszerre. Vagyis nem lehet velük mit kezdeni az ellentmondásosságuk miatt.
Tehát a gyurmázási művelet a topológiában a véges objektumok korlátozott mértékű geometriai átalakítása, új alakzatba rendezése. Ez az információ tartalmának részbeni megváltoztatását jelenti, ami minőségi átalakítás.
8. A FELÜLET GYURMÁZÁSA
Az (időbeli) elforgatási művelet egyes pillanatait térben ábrázolva azt látjuk, hogy az egyenértékű a térbeli deformációval (gyurmázással), vagyis a határolófelület nyújtásával adott irányokban. Az eltolás és elforgatás elemi műveletei tehát megfeleltethetők a felület gyurmázásának, amiket kombinálva egymással mindenféle elmozdulás létrehozható (pl. csavarodás) a téridőben. A témával részletesen A tér fizikai szerkezete és A tér matematikai szerkezete című írásokban foglalkozunk.
Az üres nD-s körök gyurmázásával a következő objektumokat kaphatjuk.:
Az 1D-s körszakasz végpontjainak elnyújtása 2D-ben egy 1D-s körvonalat ad (2D-s üres kört).
A 2D-s körvonal szélének elnyújtása 3D-ben egy 2D-s gömbi felületet ad (3D-s üres gömböt).
A 3D-s gömb felületének elnyújtása 4D-ben egy 3D-s gömbi térfogatot ad (4D-s üres hipergömböt).
A 4D-s hipergömb térfogatának elnyújtása 5D-ben egy 4D-s hipergömbi túltérfogatot ad (5D-s üres extragömböt).
Az 5D-s extragömb túltérfogatának elnyújtása 6D-ben egy 5D-s extragömbi kültérfogatot ad (6D-s üres ultragömböt).
A 6D-s ultragömb kültérfogatának elnyújtása 7D-ben egy 6D-s ultragömbi feltérfogatot ad (7D-s üres gömböt).
A nyújtást n+1D-ben mindig két irányba kell végezni, az alkotó (határoló) globális kiterjedésére merőlegesen.
A tömör nD-s körök gyurmázásával pedig a következő objektumokat kaphatjuk.:
Egy 1D-s körszakasz élének nyújtása 2D-ben egy 2D-s tömör körlapot ad.
Egy 2D-s körlap felületének nyújtása 3D-ben egy 3D-s tömör gömböt ad.
Egy 3D-s gömb térfogatának nyújtása 4D-ben egy 4D-s tömör hipergömböt ad.
Egy 4D-s hipergömb túltérfogatának nyújtása 5D-ben egy 5D-s tömör extragömböt ad.
Egy 5D-s extragömb kültérfogatának nyújtása 6D-ben egy 6D-s tömör ultragömböt ad.
A nyújtást n+1D-ben mindig két irányba kell végezni, az alkotó (belső tartomány) globális kiterjedésére merőlegesen.
Időfizikai kiegészítések:
Egy gyűrű alakú szalag (akárcsak egy körvonal) körbeforgatva (időben széthúzva) üres gömböt ad, ami egyenértékű azzal, ha a szalag két szélét gyurmázással összehúzzuk pontnyi kicsinységűre (térben széthúzzuk), majd ragasztással eltűntetjük az éleket. Ezen a módon lehet a Möbius-szalagból Mandut készíteni. Az n dimenziós objektumok 180 fokos elforgatása n+1D-ben amúgy egyenértékű a tükrözési művelettel, amivel bővebben a Tükrözés n dimenzióban című írásban foglalkozunk.
Ha az időforrás (Mandu) egyoldalú, a Bindu pedig két oldalú, akkor ez csakis úgy lehetséges, hogy valójában három pontból áll: a két egymás számára létező pontból és egy harmadikból, ahonnan (kívülről) szemléljük őket. A jelenpontokból kiáradó időhullámok gömbszférái csak abban az esetben lesznek kétoldalúak, ha legalább három pontnyi vastagságú minden egyes eseményhorizont rétegük. A kétoldalú felületek taszítják a jelenpontokat, de átjárhatók a számukra (átlyukaszthatók erővel), míg az egyoldalú felületek nem taszítják a jelenpontokat és nem átjárhatók a számukra (mert nincs mit átlyukasztani). Ezért nem képesek a jelenpontok egymáson áthatolni, míg a múlthullámokon igen.
Készült: 2006.06.03. - 2007.10.16.
Következő írás
Vissza a tartalomhoz