1. ÁTHATOLÁSOK
Emeljünk ki egy 2D-s tárgyat a saját síkuniverzumából a 3D-be, majd 90 fokkal forgassuk el hozzá képest és lassan toljuk keresztül a világán. Azt látjuk, hogy a tárgy mindig csak egy 1D-s szakasz mentén fogja metszeni a létsíkját, tehát az ott élő megfigyelők egy eszményien vékony metszetet látnak belőle, melynek hossza a tárgy profiljától függ. Ha a tárgy belül üres, a szakasz ketté is szakadhat, majd újra egyesül az áthatolás egyes pillanataiban.
Ugyanez történik egy dimenziószinttel lejjebb, ha egy szakaszt kiemelünk a száluniverzumból a 2D-be, majd 90 fokkal elfordítva visszatoljuk. A metszet egy 0D-s pont lesz. Ha a szakasz pontjai eltérő időpontok (például t1-től tn-ig), akkor a létszálban tartózkodó megfigyelő számára az áthatolás egy pont időbeli mozgásaként fog realizálódni. Előre vagy hátra az áthatolás irányától függően. Ezen a módon tehát előidézhető annak az illúziója, hogy egy n dimenziós objektum n-1 dimenziós metszete az időben hátrafelé látszódjon mozogni.
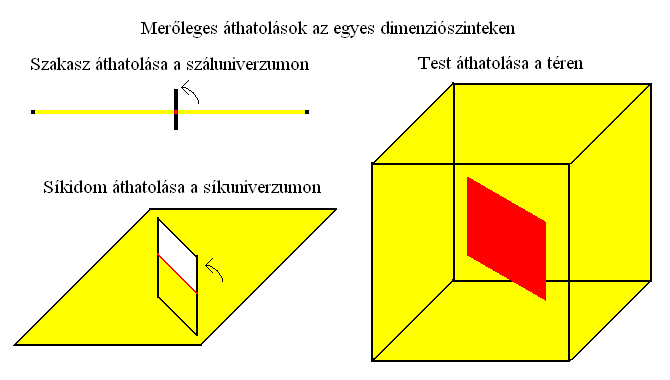
Egy 3D-s tárgyat kiemelve a 4D-be, majd 90 fokkal elfordítva és visszatolva egy 2D-s síkmetszeti kép jelenik meg a térben. Gyakorlatilag bele lehet látni a test belsejébe, mintha felszeletelnénk azt. Az orvostudományban minden eddiginél tökéletesebb passzív diagnosztikai rendszerként lenne használható a módszer, sőt ezen a módon operálni is lehetne, anélkül, hogy fel kellene vágni a beteget. Ha makro méretekben is alkalmazható a beágyazási környezet lokális elforgatása, akkor nem csak a kulcsát vesztett páncélszekrényekbe lehet ezen a módon belenézni (esetleg betenni vagy kivenni dolgokat), hanem a kisebb aszteroidák ásványianyag tartalma is felmérhető lesz, gravitációs távcső nélkül. Ennek megfelelően természetesen egy 4D-s ember az 5D-be kiemelve és elforgatva egy 3D-s metszetnek fog látszódni (tömör vagy üreges testnek).
Az áthatolási folyamat hasonló ahhoz, amikor egy 4D-s hipertest a 3D-s altéren megy keresztül, arra merőlegesen. A 3D-ben látható metszete rendes térbeli testnek fog tűnni, ami azonban anomáliásan viselkedik. Hirtelen jelenik meg a semmiből (mintha oda teleportálódott volna), majd az alakját, méretét, struktúráját változtatva folyamatosan átalakul, esetleg a felismerhetetlenségig megváltozik, hogy végül nyomtalanul eltűnjön a semmiben. Ezen művelet biológiai következményeivel korábban már részletesen foglalkoztunk Az élő szervezetek alkotóelemei című szakmunkában (szerző: Varga Endre, Eseményhorizont, 2001).
2. SZABÁLYOK
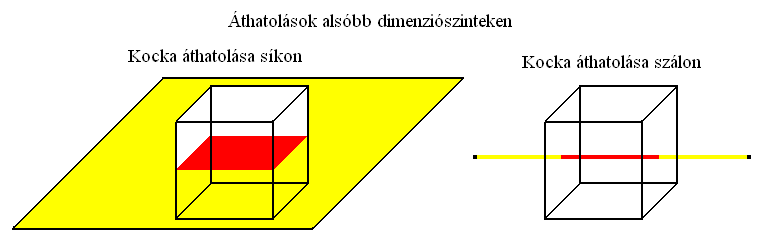
Általános szabályként azt mondhatjuk, hogy minden n dimenziós objektum áttolható az összes alacsonyabb dimenziószámú altéren, ahol az alakjától függően különböző deformációkat fog mutatni, olyan mozgásokat (parajelenségeket) produkálva, ami az adott beágyazási környezetben normálisan nem lehetséges. Ha viszont teljes metszeti képet szeretnénk kapni az objektumról egyetlen áttolási művelet során, akkor csak n-1D-ben tehetjük meg ezt. Egy 3D-s test egyenes vonalú mozgással áthatolhat a 2D-n úgy, hogy közben minden pontja metszi a síkot és ezáltal vizsgálható, de az 1D-s szálat így nem képes metszeni. Nagyon sokszor kellene a testnek újra és újra átmennie a szálon, mindig egy kicsit eltolódva a síkban ahhoz, hogy minden pontjáról képet kaphassanak az 1D-s megfigyelők.
Ebből következik, hogy még ha sikerül is lokális dimenziókonvertereket építenünk, hatékonyan csak a 4D-s dolgok megfigyelésére használhatjuk majd. Az 5D-s és magasabb kiterjedési számú objektumok metszéssel való elemzése szinte megoldhatatlanul nehéz és körülményes feladat lesz (bár nem lehetetlen). Ennek a törvényszerűségnek többek között a térablakok fejlesztésénél lesz nagy jelentősége, mivel az átjáró sík felületén csak 3D-s testek képesek zavartalanul áthatolni. Az emberi test aurája (nem beszélve a lélekről) viszont 4D-s, így igényelni fogja a térbeli átjárót, amihez azonban 6D-s technológiára van szükség. A témával részletesen a térkapuk működését ismertető emanikai cikkekben foglalkozunk majd.
3. VESZÉLYEK
A kiterjedésre merőleges áthatolások esetén felmerül a kérdés, hogy vajon a forgó rendszerek (anyag, fény) időhurkai nem okozhatnak annihilációs robbanást azzal, hogy áthatolnak egy altéren? Ilyen veszély főként akkor áll fenn, ha az n+1D-s felsőtérbe kiemelt nD-s objektumot 90 foknál nagyobb mértékben elforgatva toljuk át a közegén. Ha bármely alkotója (részecskéje) akár csak időlegesen is elfordul a helyén és beáll a közeg kiterjedésébe, például a szeparátor rétegek kényszerítő ereje miatt, akkor azonnal antianyaggá válik. Mindezek miatt valószínű, hogy áthatolásokat csak 90 fok alatti elforgatásokkal szabad előidézni a gyakorlatban.
Más a helyzet egy 4D-s anyagú testtel, aminek alkotóelemei a 3D-s altérben könnyen megjelenhetnek antianyagként. Abban az esetben, ha a 3D-s anyagi részecskék a hullámterükkel fizikai kölcsönhatásba lépnek a 4D-s anyagokkal, az efféle áthatolások potenciális veszélyt jelentenek, elsősorban a 3D-s világra. Éppen ezért mindig a magasabb dimenziószinten létező élőlények (intelligenciák) felelőssége, hogy odafigyeljenek az efféle veszélyekre és lehetőleg kerüljék az áthatolásokat az altereken.
A mi számunkra ennek akkor lesz jelentősége, ha a dimenziókonvertereinkkel létrehozott lokális 4D-s túltérben kísérletezni kezdünk a különféle anyagokkal. De ezzel majd más emanikai írásokban foglalkozunk részletesen.
Készült: 2005.11.26.
Következő írás
Vissza a tartalomhoz