A TÉR MATEMATIKAI SZERKEZETE


1. BEVEZETÉS

A dimenzió szó jelentése: térbeli kiterjedés, méret, nagyság, arány. A klasszikus fizikában alapdimenziónak tekintik a hosszúságot (teret), a tömeget és az időt. A fizikai kiterjedésnek, azaz a térnek jelenleg négyféle leírását ismerjük a matematikában és a fizikában egyaránt, bár az újabbakat nem használjuk valamiért. Közben mindenki gondosan megfeledkezik arról, hogy a fizikai és matematikai tér két teljesen különböző dolog, melyek közt létrehozható logikai kapcsolat, de ettől még nem lesznek azonosak. Ezek a konstrukciók a következők.:
A legrégebbi az euklideszi tér, ami egyszerű, háromdimenziós kontinuum, folytonos pontsokaság, és a Descartes-féle sík koordináta-rendszer térbeli kiterjesztése. Sajnos a gyakorlatban, a valódi világ leírására ez tökéletesen alkalmatlan, mivel statikus, időtlen, és valójában pontszerű, tehát semekkora. Lásd: A pontról című írást.
A másik, újabb térkonstrukció a Hermann Minkowski-féle négydimenziós téridő-kontinuum. Lényegében az euklideszi tér egyszerű kibővítése az idővel, ami skalárisan mindenfelé terjed az origóból. Ebbe később még beleerőszakolták a tömegpontokat is, hogy ízlés szerint görbítgethető legyen a már eleve rosszul felépített koordináta-rendszer. Itt az egymástól korábban teljesen különbözőnek definiált jelenségeket (teret, időt, tömeget) kapcsolták össze önkényesen, hogy áthidaló megoldást találjanak a felmerülő problémákra (sikertelenül).
A harmadik, nem euklideszi geometriai modell, aminek több típusa is van (pl.: a Riemann-féle elliptikus geometria, a Bolyai-Lobacsevszkij-féle hiperbolikus geometria), három nagy matematikus találmánya. Nyikolaj Ivanovics Lobacsevszkij, Bolyai János és Bernhard Riemann a XIX. század közepén dolgozták ki, egymástól függetlenül a pozitív és negatív görbületű terek matematikáját, amelyeknek aztán nagy szerep jutott a relativitás elmélet megalkotásában.
A negyedik, még bonyolultabb modell a XX. század végén már nagyon közel jutott a jó megoldáshoz, de valamiért nem tudott széles körben elterjedni a fejekben és tovább fejlődni. Sem Andrej Dmitrijevics Szaharov orosz atomfizikus párhuzamos univerzumainak spirálgömbi terei, sem John Archibald Wheeler amerikai atomfizikus egyesített térelmélete a félspínű térszerkezetről nem vált elfogadottá, ahogy Kisfaludy György magyar feltaláló ezekre épülő transzcendens téridő modellje is megmaradt az elmélet szintjén. Ha történtek is gyakorlati kutatások és továbblépések a tér szerkezetének megismerése érdekében, ezek valószínűleg megmaradtak a katonai programok leple alatt. Az iskolákban pedig továbbra is a régi, száz évesnél idősebb elgondolásokat oktatják "korszerű tudomány" címszó alatt. Hivatalosan tehát itt tart ma a fizika és a matematika dimenzió szemlélete, jócskán lemaradva a tényleges tapasztalatok (parajelenségek) diktálta igények mögött.
Mindegyik modell közös hibája, hogy egybemossák a matematikai és fizikai kiterjedéseket, azt feltételezve (minden alap nélkül), hogy ha a fizikai térben ábrázolhatók ezek a matematikai terek, akkor bizonyára ilyen lesz a fizikai tér szerkezete is. A hibás elképzelést az első három modellnél például az okozta a tudós fejekben, hogy a teret egyszerű, jellegtelen kiterjedésnek tekintették. Ürességnek, hézagnak a létező dolgok között, ami önmagában tulajdonképpen nem is létezik, tehát csak egy absztrakt fogalom. Erre pedig bármilyen struktúra ráhúzható tetszés szerint, hogy aztán kedvünkre görbítgessük, hajlítgassuk és mindenféle trükköket megcsináljunk vele, függetlenül a tényleges valóságtól.
Az időfizika által életre hívott időmatematikai modellekben szerencsére nem így gondolkodunk, ezért készítettünk egy sokkal jobb, mindenki számára könnyen érthető, átlátható és használható, valódi (nem fiktív) téridőt. Ami dinamikus, időben létező, van benne forgásjelenség és tényleges, struktúrált kiterjedés, továbbá simán kiküszöböli a pontszerűségből fakadó problémákat is. Ebben az írásunkban a tér időgeometriai szerkezetét szeretnénk tömören és a teljesség igénye nélkül bemutatni. Anyagunk szorosan kapcsolódik a három pont tételhez, az n dimenziós forgáshoz és tükrözésekhez, valamint más korábbi publikációkhoz, ezért feltételezzük, hogy az Olvasó már ismeri ezeket a levezetéseket.
Mi nem dobálózunk bonyolult matematikai képletekkel és elvont okoskodásokkal, mivel a megértéshez ezek fölöslegesek. A világegyetem alapvető jelenségei mind igen egyszerűek, bárki által könnyen felfoghatóak. Csak a rájuk épülő összetettebb rendszerek komplexitása kíván mélyebb szintű ismereteket a szemlélőjüktől. Nagyon fontosnak tartjuk tehát, hogy pontosan tisztázzuk az alapokat, mert ennek ismeretében lesz esélyünk megbírkózni a felépítménnyel.
A valódi téridőnek van egy fizikai szerkezete, amivel külön írásban foglalkozunk, és ennek alapján elkészíthető a téridő matematikai szerkezetének modellje, ami hasonló hozzá, de nem azonos vele. Mindkét modell más célokra használható és logikailag szorosan összefüggenek. A legfontosabb kijelentés, amit a téridővel kapcsolatban meg kell tennünk az, hogy ha a téridő létezik, akkor annak valamilyen formája, struktúrája kell, hogy legyen.

2. MŰVELETEK A PONTTAL - AZ IDŐSZÁL


Induljunk el (szokás szerint) a kezdeti létezőből, a Pontból, aminek nincs kiterjedése, ezért csupán az időben létezik. Az Eseményhorizont korábbi írásaiban már részletesen kifejtettük ennek a pontnak a tulajdonságait. Most azt nézzük meg, mit lehet csinálni (időben) egy ilyen Ponttal, aminek eredményeképpen kiterjedéssel (dimenzióval) rendelkező dolgok lesznek belőle.
Azt tudjuk, hogy egyenest nem lehet 0D-s pontok puszta (térbeli) egymás mellé helyezgetésével készíteni, mert az szintén 0D-s lesz. De mi van akkor, ha egy 0D-s, időben létező Pontot önmagához képest elcsúsztatunk? Lásd: a Kezdeti megnyilvánulások című írásban az álló VÍZ elmozdulását az első realizáció pillanatában. A mozgás időben történik, nem térben, mivel a Pont időben létezik (csak időbeli kiterjedése van). Az elmozdulás sebességét vegyük egynek (E=1=RV, ahol E az emanáció mértéke, RV a relatív sebesség). Ez valamely véges érték, mértékegység nélkül. Ekkor egy olyan időegyenest kapunk, amelyen bármely két időpont közötti távolság véges és végtelen egyszerre, mert véges sebességű mozgással csak véges időbeli távolságra nyúlhat az egyenes, ugyanakkor viszont végtelen sok pont található a kettő közötti szakaszon. Ennek az egyenesnek van kiterjedése, mivel a vége felé folyamatosan (ki)terjed, nyúlik, vagyis a hossza potenciálisan (de sohasem aktuálisan, ténylegesen) végtelen. (1. ábra)


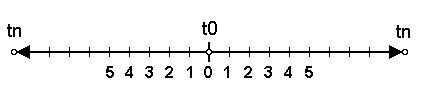
Az így kapott 1D-s kiterjedés az időszál, a szálszerű univerzum. Ezen egyetlen pont önmagában mindig időtlen, mert nulla hosszt foglal el az egyenesből. Tehát a Pont valójában időtlen. Ez pedig ellentmondásban van a kiindulási állításunkkal, a Pont időbeli létezésével. A megoldás erre a következő.: amíg a Pont áll (a VÍZ megnyilvánulatlan), addig csak van, időtlenül, de nem létezik. Amikor mozogni kezd (az első realizáció miatt), egyenessé nyúlik, akkor jelenik meg az időtartam, a létezés. Tehát ha mozogni csak időben lehet, akkor ez fordítva is érvényes: idő csak ott van, ahol mozgás van. Az időszál tehát létezik.
Első megjegyzés: Ha a mozgást térbeli megnyilvánulásnak tekintjük, akkor elmondhatjuk, hogy a tér (kiterjedés) is csak az időben létezik, vagyis nincs értelme külön tér és idő dimenziókról beszélni! Fordítva megfogalmazva az állítást: Idő csak ott van, ahol tér (mozgás) is van, és tér csak akkor jön létre, ha valami az időben létezik. Időtlen tér vagy teretlen idő vagy időtlen mozgás, teretlen mozgás tehát nem létezik. Az idő és a tér ezért egymás duálisai, ugyanazon jelenségnek, a létezésnek két praktikus leképzése.
Ha ezen az időegyenesen a pontot tekintjük mértékegységnek, akkor nincs véges távolság, csak végtelen, mivel a pontok sűrűsége is az. Konkrétan: egy 1 cm-es és egy 2 cm-es szakaszt egyaránt végtelen számú pont alkot. Ha viszont egy tetszőleges (időben véges) szakaszt teszünk mértékegységgé kvantálással, (pl.: 1 cm), akkor csak véges távolságok vannak az egyenesen.
Jó kérdés ezek után, hogy ha mindent egy véges szakasszal mérünk a rendszerünkben, akkor ennek a stabilitását, állandóságát, hosszát hogyan ellenőrizzük, rögzítjük? És mihez képest? Ha a mértékegységet önkényesen jelöltük ki (valamely véges szakasz a végtelen egyenesen), akkor minden további, ebből következő dolog is önkényes lesz. Ezért nagyon fontos, hogy a dimenziórendszer belső struktúráját pontosan megismerjük, feltárjuk, mert csak ezáltal tudunk törvényszerű (a rendszer belső logikájából következő) levezetéseket készíteni a gyakorlati hasznosításhoz. A témával részletesen a Bindu forgásának elemzésekor már foglalkoztunk, ahol az időforrás egyedi forgási sebességéből vezettük le az etalon saját frekvenciát, mint alapmértéket.
Második megjegyzés: Amennyiben mértékegységül a későbbi rendszerünkben egy attraktor (időhurok) behúzási tartományát választjuk, ami folyton változik két határérték között, ennek ingadozása pontatlanná teszi ugyan a ráépülő műveleteinket, viszont a kellően nagy mérettartományokban elhanyagolhatóvá válik ez az eltérés, ha az igényelt pontosságot nem haladja meg. A végtelen pontsűrűségű egyenes fraktális felépítésű, analóg (folytonos), de modellezhető igény szerint diszkréten is, lásd: a Gondolatok a végtelenről című írást. Ezen a különféle mérettartományok összehasonlításával jól megfigyelhető a skálahasonlóság törvénye. Az ilyen (kétfelé nyúló) egyenes alkalmas rá, hogy ábrázoljuk rajta a valós számokat.

3. A KÖR ÉS AZ EGYENES KAPCSOLATA


Az időbeli mozgás irányultsága kétféle lehet az egyenes két végéből fakadóan. Ha a nyúló időegyenes egy időpontból indult, akkor a két végén, mivel kitüntetett irány nincs, mindig egy időpont, időpillanat található. Mivel pedig korábban azt mondtuk, hogy a pont mozgatása időben történik, és az egyenes pontjai a saját idejükben különböznek csak egymástól, ezért ha két pont egy időpillanatban létezik, akkor azok egy helyen is kell legyenek az időtérben. Az egyenes tehát a két végén körbezárt, vagyis kör.
A körnek van egy olyan tulajdonsága, hogy bár a végtelenségig lehet rajta körbejárni, mégis ciklikus természetű. Egy véges körön haladva mindig ugyanazok az időpillanatok ismétlődnek a szemlélő számára újra és újra, oda-vissza (t0-tól tn-ig, majd tovább t0-ig egy kör alatt). Rajta minden pontnak megvan a maga azonos idejű párja, pontosan a kör túloldalán (tehát egy kör alatt kétszer haladok át minden pillanaton). Ha viszont ez igaz, akkor a jelenpont, amely az egyenesnél a két végpont, a körnél viszont egy helyre esik (tn), párban áll a túloldalon található kiindulási ponttal, az első időbeli pillanattal (t0). (2. ábra)
Kívülről nézve ez azt jelenti, hogy mind az egyenes, mind a kör lényegében időtlen, hisz ha a t0 pont és az egyenes két végén szaladó jelenidőpont egy pillanat, akkor ami köztük van, az is egy velük. Tehát az egyenes és a kör is csak egy pont (kívülről). Belülről viszont végtelennek mutatkozik a konstrukció. Ez az állítás minden későbbi rendszerre is érvényes lesz, amit az időszálból építeni fogunk, vagyis a teremtés csak belülről mutatkozik univerzumnak a szemlélő számára, kívülről nézve mindvégig egy pont marad!


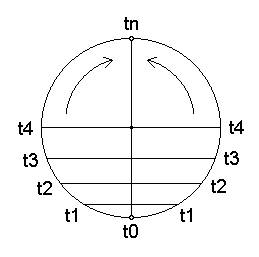
Az időszál egyenese, illetve köre egyaránt potenciálisan végtelen, vagyis egyenértékű, de geometriailag nem egyforma. A véges hosszú egyenes (szakasz) a szemlélő számára úgy tűnhet, hogy részét képezi a végtelen kerületi hosszúságú körnek. A véges szakasz a végtelen körvonalnak persze csupán végtelenül kicsiny részét foglalja el, de pont ezért látszik a görbülete nullának. A véges kerületű kör viszont egy végtelen hosszú egyenessel összehasonlítva végtelenül kicsinek, azaz gyakorlatilag pontnyinak látszik. Így a létező legkisebb méretű (három pontnyi) véges kör a végtelen egyenes egy darabjával (kvázi pontjával) lesz azonos (látszólag). Az időszál egyenese tehát egy másféle leképzésben egyenértékűnek mutatkozik egy forgó időponttal.
Az időbeli mozgás mindig valamilyen tengelyhez, irányvektorhoz kapcsolódik. Mivel maga a tengely is egy egyenes, ezért az alkalmazása nem igényli újabb elemek önkényes bevezetését a modellünk továbbfejlesztéséhez. Mielőtt azonban tovább mennénk, előbb definiáljuk a tengely fogalmát. A tengely olyan egyenes, amely körül valami elmozdul egy körvonal mentén. Relatív rotációt (RR) végez, tehát forog vagy kering. A vektor iránnyal és nagysággal jellemezhető matematikai mennyiség, lényegében egy irányított egyenes szakasz, amit a geometriában alkalmazunk a mozgások leírására, ábrázolására.
A fenti meghatározásokból egyértelműen következik, hogy a mozgás alapvetően kétféle lehet: eltolás az egyenes mentén vagy forgatás az egyenes körül. Ha csak önmagában alkalmazzuk egyik vagy másik műveletet a ponton, nincs értelme irányultságról (eltolásnál előre-hátra, forgatásnál jobbra-balra) beszélni, mert a pont szimmetriája miatt minden irány egyenértékűnek és egyformának mutatkozik. Egyszerű 180 fokos elforgatással az előre irány azonos lesz a hátra iránnyal, a balra forgatás a jobbra forgatással. A kétféle művelet kombinálásakor viszont megjelenik a tükrözési szimmetria, és négyféle, egymással párosan fedésbe hozható egyenest kapunk. Az előre mozgó balos egyenes elforgatással azonos lesz a hátra mozgó jobbossal, míg az előre mozgó jobbos a hátra mozgó balossal. A két páros egymás tükörképe lesz.
Minden attól függ tehát, hogy a kezdeti Pontot, a vanást milyen műveletekkel mozgatjuk meg az időben. Ezen műveletek együttes alkalmazása viszont számos kérdést vet fel, melyeket feltétlenül tisztáznunk kell, mielőtt alkalmazni kezdjük őket.

4. LEKÉPZÉSI LEHETŐSÉGEK


Számos lehetőségünk adódik arra, hogy a kombinált műveleteket hogyan végezzük el a Ponton, illetve geometriailag ezt miként ábrázoljuk a leképzésnél. Mivel az alkalmazott modellünk az időben folytonosan létezik, a rendszer dinamizmusa miatt különbség mutatkozik aközött, hogy mit csinálunk a Ponttal és mit ábrázolunk mindebből.
A klasszikus (egyszerű) matematikai és fizikai síkok, terek esetében ilyen problémák nem merülnek fel, mert azok statikusak és gyakorlatilag fiktívek (kitaláltak), ráadásul nem a tényleges kiterjedés lemodellezése céljából készültek, hanem más műveletek, függvények, síkidomok ábrázolásához. A mi célunk viszont jelenleg nem az, hogy legyen egy valamilyen "rajzlapunk", amin dolgozhatunk, hanem, hogy létrehozzuk azokat a "rajzlapokat", azokat a (valóságot legjobban megközelítő) síkokat és tereket, amik majd később alkalmasak lesznek a valóságban (a teremtésben) megfigyelhető dolgok célirányos ábrázolására.
Most vegyük sorra a lehetséges leképzéseket és a belőlük fakadó sajátos problémákat.:

4.1. A LEKÉPZÉS ÁBRÁZOLÁSA

Először is nem mindegy, hogy az egyes műveleteket az időben egyszerre vagy egymás után, és milyen sorrendben végezzük el. Nem ugyanaz lesz a végeredmény, ha a pontból eltolással előbb egyenes lesz, majd ezt egyszer körbeforgatjuk (sima időszál) vagy ha eltolás közben folyamatosan forgatjuk a nyúló egyenest (csavarodó időszál).
Az időben egyszerre történő mozgatás ábrázolása szintén többféle lehet. Vegyünk egy egyszerű és szemléletes példát: két eltolás, egymásra merőleges tengelyek mentén. Itt négy különböző lehetőségünk van az eredmény ábrázolására.:

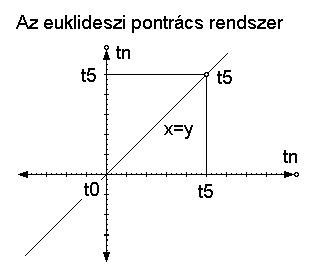
4.1.1. Ha a két irányú mozgást az időben egymás után végezzük el, de csak a végeredményt ábrázoljuk a leképzésben, akkor egy négyzetes síkot fogunk kapni, ami gyakorlatilag megfelel az XY koordináta-rendszernek. Ez az euklideszi sík, ami egy pontokból álló rácsrendszer. Itt vagy két pontot kapunk, melyek egymásra merőleges irányban távolodnak a közös t0 ponttól vagy egy magányos harmadikat az X=Y egyenes mentén, átlósan mozogva. Ez utóbbi viszont azonos az egyszerű eltolással, hisz a rendszer továbbra is pontszimmetrikus. (3. ábra)


4.1.2. Ugyanezt a négyzetes síkot kapjuk akkor is, ha a két irányú eltolást végtelenül kicsiny elemi (pontnyi) lépésekre bontjuk, és ezeket felváltva végezzük el, mindig a meglévő rendszer egészén alkalmazva őket. Látszólag a két módszer nem különbözik egymástól, de a forgás bevezetésekor azonnal kiderülnek a különbségek. Az első módszernél alkalmazva az elforgatást egy sima körlapot kapunk (körbeforgatott négyzetes síkot), míg itt egy spirálisan csavarodó körlap lesz az eredmény. (4. ábra)


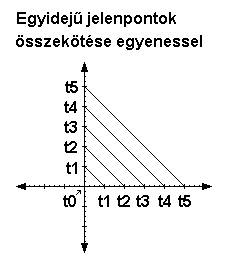
4.1.3. Azt is megtehetjük, hogy a két irányú eltolást elemi lépésenként, felváltva végezzük ugyan, de az ábrázolást nem alkalmazzuk az egész rendszeren, hanem csak az egyidejű pontok közti kapcsolatot jelöljük összekötő egyenesekkel. Ebben az esetben egy egyenlő szárú derékszögű háromszöget kapunk, aminek befogói a két eltolási tengellyel azonosak. (5. ábra) Ha ezt közben még forgatjuk is, akkor egy növekvő négyzethalmazt (6. ábra) kapunk.


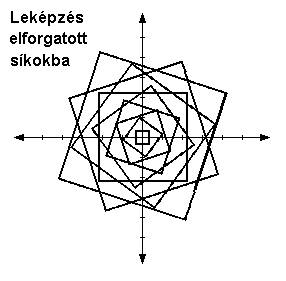
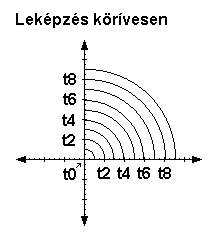
4.1.4. A két eltolási tengely által bezárt szögtartományban szintén alkalmazzuk az eltolást, egyszerre és azonos sebességgel minden irányban. Ezt lépésenként ábrázolva egy növekvő negyedkörívet kapunk, amit kiterjesztve minden eltolási irányba körkörös síklap lesz az eredmény. Ha a kiterjesztést az elforgatás segítségével végezzük, akkor viszont spirálisan csavarodó, körkörös síklapot kapunk, mint a második esetben. (7. ábra)


4.2. A MŰVELETI SEBESSÉG

A dinamikus leképzésnek számos további paramétere van még. Ilyen az egyes műveleti sebességek, vagyis az időegység alatt végzett eltolások, illetve szögelfordulások mértéke, valamint ezek egymáshoz való viszonya és aránya. Mivel korábban az elmozdulás sebességét vettük alapmértéknek (E=1), ami az idő telésével, az időszál nyúlási sebességével azonos, célszerűnek tűnik ezt meghagyni alapértelmezésben. Az ettől eltérő, torzított rendszerekkel (most még) ne foglalkozzunk.
A fő problémánk itt abból adódik, hogy a forgás sebessége (RR) milyen viszonyban van az eltolással. Ha ugyanis az egységnyi eltolás egyenértékű az egységnyi elfordulással (RV=1=RR), akkor ez kétféle leképzést tesz lehetővé, attól függően, hogyan értelmezzük az egységnyi elfordulást.

4.2.1. Ha a forgatást az aktuális rendszert alkotó minden pontra külön értelmezzük, azok mind egységnyi kerületi sebességgel mozdulnak el a közös tengely körül. Ebben az esetben az egységnyi kerületi hosszúságú körnek a sugara: 0,159154943... lesz, vagyis 1/(2*Pi). A sugár növekedésével a rendszert alkotó pontok egyre kisebb szögelfordulásokat (RR= relatív rotáció) végeznek a tengely körül, tehát egy spirálisan felcsavarodó síkot, illetve teret fogunk kapni, aminek egyenletes (lineáris) a menetemelkedése.

4.2.2. Ha a forgatást az egész aktuális rendszerre alkalmazzuk, azt egységes (szilárd testnek) tekintve, akkor értelemszerűen kifelé haladva gyorsulni fog a pontok kerületi sebessége. Ez a végtelenben végtelen sebességet jelent, ami viszont időtlen mozgást feltételez, tehát kizárandó a valós (dinamikus, időbeli) modellek közül.

4.3. A TENGELYEK HELYZETE

Több művelet együttes alkalmazásánál felmerül a tengelyek egymáshoz viszonyított helyzetének kérdése. Több tengely lehet egymással párhuzamos (pl. amikor egy eltolási és egy forgatási tengely egybeesik) vagy merőleges. Természetesen nincs értelme annak, hogy két eltolási tengely vagy két forgatási tengely egymásra essen, mivel ezek a leképzéstől függően két dolgot eredményezhetnek.:

4.3.1. Nem csinálnak semmit, tehát az idő mozgási sebessége változatlan marad a forgással együtt (E=1, RR=360 fok, tehát E=RR).

4.3.2. Gyorsítják a műveleti sebességet, megduplázva a mozgást és az elfordulást (E=2, RR=720 fok, ahol szintén E=RR). Ennek következményeit (az időgeometria torzulását) ebben az írásban külön nem vizsgáljuk.

Abban az esetben, ha egy balra forgó eltolási tengely egybe esik egy jobbra forgóval, a két művelet vektorai kioltják egymást és gyakorlatilag nem történik semmi, ezért ezzel a lehetőséggel nem kell külön foglalkoznunk.
Fontos kérdés viszont, hogy a forgástengelyek egymást is forgatják vagy nem, illetve az eltolási tengelyeket forgatják vagy nem? Ahhoz, hogy ezekre a kérdésekre egyértelmű válaszokat kaphassunk, előbb a műveletek kombinálásából fakadó lehetőségeket kell megvizsgálnunk.
Több művelet együttes alkalmazásakor nagyon nem mindegy, hogy a műveletek tengelye melyik jelenponton megy át. A kiindulási t0 ponton vagy az időben mozgó, az egyenes aktuális végén található tn ponton?
Harmadik megjegyzés: Azzal a lehetőséggel (ugyancsak) ne foglalkozzunk, hogy megosszuk a műveleteket több pont között. Ezt a témakört majd egy külön írásban fogjuk tárgyalni, amikor az egymásba ágyazott terek kölcsönhatását és szerkezetét vizsgáljuk: a párhuzamos tereket, az egymástól függetlenül működőket (egyenrangú terek kapcsolata) és a térben születő altereket.
Amennyiben a tengelyek a t0 ponton haladnak át (metszik egymást), a műveletek eredményét a leképzésben ehhez képest (a tér origójához) értelmezzük és ábrázoljuk. Ekkor az origóból kifelé haladva az idő előre (múlttól a jövő felé) telik tn irányába. Ez az egyszerűbb megoldás. Példa: 1 eltolás és 1 forgatás (rá merőlegesen) egy spirális síkot ad. Ha viszont a mindenkori tn pontra illesztjük a tengelyeket, a keletkező térben az idő iránya fordított lesz: az origóból kilépve hátrafelé telik, tn-től t0-hoz (az aktuális jelentől a múlt felé). A tn-re illesztett tengelyeknél továbbá felmerül az a kérdés is, hogy a műveletek végrehajtásakor keletkező sík pontjai közül melyik legyen az a tn, amire illesztünk? Vagy egy pont helyett az összesre egyszerre végezzük el az illesztést? Ez túl sok bonyodalommal járna és ráadásul semmi sem indokolja az alkalmazását. Egy példa az egy pontra illesztés esetére: Ha az eltolási egyenes aktuális végpontjába állítjuk a forgatási tengelyt, egy olyan spirális síkot kapunk, amely ugyan azonos a t0 origójú spirálsíkkal, csak éppen benne az idő visszafelé folyik, mozog. (8, 9. ábrák)


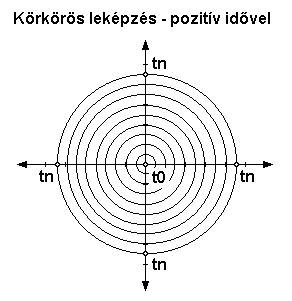
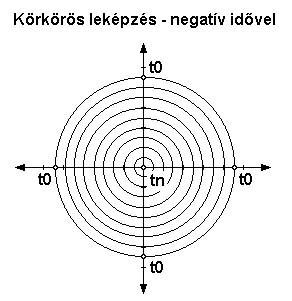
Mindezen megfontolások alapján, figyelembe véve az egyszerűséget és az átláthatóságot, valamint azt, hogy a t0 pont időben azonos a tn ponttal, alapértelmezésben válasszuk a t0 pontot metsző tengelyek használatát. Ebből következően pedig automatikusan adódik a válasz a korábbi kérdésünkre is.: A forgástengelyek egymást és az eltolási tengelyeket is elforgatják.
Végezetül még látnunk kell, hogy a leképzésnél sokat számít az is, hogy a tengely, amely mentén az aktuális műveletet elvégezzük, hogyan helyezkedik el a már meglévő rendszerhez képest. A tengely vonala (az egyenes) vagy beleesik a rendszer dimenziójába vagy nem (kinyúlik belőle magasabb dimenzióba). Ennek következményeit összefoglalva lásd később: A műveleti szabályok című 10. fejezetben.

5. A VALÓS LEKÉPZÉS


Az eddigi lehetőségeinket számba véve jogosan merül fel bennünk az igény, hogy csoportosítsuk a különféle tereket, és azok leképzéseit, valamint próbáljuk meghatározni a valóságos létezőre leginkább hasonlító, azt minél pontosabban ábrázoló dimenziószerkezet paramétereit. Kezdjük először a valóságos létező időtereinek tulajdonságaival.:

5.1. Az egyes műveletek az időben egyszerre történnek, ezért azok eredményét egyszerre kell ábrázolni időegységenként. A kialakuló geometria alakjának kiszámításakor viszont mindig rögzített sorrendet kell tartani. A különféle műveletek (részlépések) prioritási (végrehajtási) sorrendje: eltolás, elforgatás, kivágás (ez utóbbit lásd később, külön publikációban). Mindennek az az oka, hogy a műveletek célja a dimenzió (kiterjedés) létrehozása, ezért mindig ez az első lépés. Az eltolás ugyanis mindig emeli a dimenziószámot, tehát ez a legfontosabb művelet. A forgatás csak bizonyos esetekben emeli, a kivágás pedig nem változtat rajta.

5.2. A valóságos geometriát legpontosabban követő ábrázolás a 4.1.4.-es módszer, amelynél egy növekvő negyedkörívet kapunk két eltolás esetén. Az elforgatással ebből spirálisan csavarodó, körkörös síklapot kapunk, ami formailag azonos az időfizikából jól ismert emanációs hullámtéri modellel.

5.3. A műveleti sebesség eltolásnál és elforgatásnál egyaránt egységnyi: (RV=RR=1), amit a 4.2.1.-es módszer szerint kell alkalmazni. Vagyis az elforgatást az aktuális rendszert alkotó minden pontra külön értelmezzük. Azok mind egységnyi kerületi sebességgel mozdulnak el a közös tengely körül.

5.4. Ha két eltolási tengely a forgatás miatt egymásra esik, a vektoraik gyakorlatilag egyesülnek, tehát a 4.3.1.-es lehetőség valósul meg. Az idő mozgási sebessége változatlan marad a forgással együtt (E=RR).

5.5. A tengelyek mindig a t0 ponton haladnak át (metszik egymást), ezért a műveletek eredményét a leképzésben ehhez képest értelmezzük és ábrázoljuk. Az idő telési iránya alapértelmezésben: előre, a múlttól a jövő felé, tn irányába.

5.6. A forgástengelyek egymást és az eltolási tengelyeket is elforgatják. Emiatt a magasabb dimenziószintek folyamatosan pulzálnak a keltési időben a különböző alsóbb síkok között, azokat is folyton újragenerálva magukból. Konkrétan: 1D, 2D, 3D, 4D, 3D, 2D, 1D, stb felváltva egzisztál egy rendszeren belül. Ennek oka az, hogy forgás közben a tengelyek szabályos időközönként egymásra esnek, és az 5.4.-es pontnak megfelelően nem összegződik a hatásuk.

6. AZ IDŐTEREK CSOPORTOSÍTÁSA

A következő feladatunk a leképzési lehetőségekből adódó időterek fajtáinak csoportosítása a legjellemzőbb paramétereik alapján. Mindenekelőtt különbséget kell tennünk a valódi időszerkezet valóságos tere és ennek különféle leképzései, nem valósághű ábrázolásai között.

6.1. Vannak valódi terek. Ennek paramétereit foglaltuk össze az 5. fejezetben. Ezek a felépítésük szerint két fő csoportba sorolhatók.

6.1.1. Természetes valódi terek. Ezek létrehozásához csak az idő szerkezeti tulajdonságaiból következő műveletek szükségesek, vagyis az eltolás és az elforgatás. A későbbi fejezetekben csak ezekkel fogunk foglalkozni.

6.1.2. Mesterséges valódi terek. A természetes tér módosításakor keletkeznek. Ilyen beavatkozás a kivágás és a torzítás. Ezek nem valóságos tereket eredményeznek.

6.2. Vannak képzetes terek. Ezeket a valódi terekből származtatjuk, az ábrázolás paramétereinek megváltoztatásával. Szintén két fő csoportból állnak.

6.2.1. Természetes képzetes terek. A természetes valódi terek ábrázolási paramétereinek megváltoztatásával kapjuk őket.

6.2.2. Mesterséges képzetes terek. A természetes képzetes terek módosításakor keletkeznek, ugyanúgy, mint a mesterséges valódi terek.

Negyedik megjegyzés: Ezt a csoportosítást a valódi és képzetes számok mintájára hoztuk létre. A természetes valódi tereken belül létezik egy olyan részhalmaz is, amit tengelypáros tereknek neveztünk el. Mert ahogyan a geometriában a kocka egy speciális hasábnak számít, úgy a térgeometriában is kiemelt szerephez jutnak azok a tértípusok, amik bizonyos szabályosságokat mutatnak.
Definíció: Tengelypáros tér az, amelyben minden eltolási tengellyel egy és csak egy forgatási tengely esik egybe.
Ezzel gyakorlatilag meghatároztuk azokat a körülményeket, melyek figyelembe vételével már egyértelműen le tudjuk képezni a térgeometriai modellünk számára a különféle, összetett időterek szerkezetét. Lássuk tehát a valós leképzésből fakadó lehetőségeket.

7. AZ IDŐSZÁL ÉS AZ IDŐSÍK

A kiindulási pontunk ismét legyen a nulla dimenziós, időtlen Pont. Mivel a tengely, aminek segítségével a dimenzióképző műveleteket elvégezzük 1D-s, nincs értelme arról beszélni, hogy a vonala beleesik-e vagy sem a pont dimenzióvilágába. Ezért ha a tengely körül megforgatom a Pontot, akkor egy időben forgó pontot kapok. Attól függően, hogy balra vagy jobbra történik a forgatás, kétféle pont az eredmény, melyek azonban egymással egyenértékűek, hisz egyszerű megfordítással (elforgatás egy másik, az előzőre merőleges tengely mentén) átvihetők egymásba. Ugyanígy ha eltolom a Pontot tetszőleges (végtelen) mértékben, egy végtelenségig nyúló, 1D-s egyenest kapok. Ebből is kétféle van, előre és hátra nyúló, melyek szintén átvihetők egymásba egyszerű megfordítással.
Most alkalmazzuk a kétféle műveletet egyszerre a Ponton. Itt már több lehetőségünk van, mivel az eltoláskor keletkező 1D-s egyenesnél már van értelme a műveleti tengely elhelyezkedésének. Ha a forgatás és az eltolás tengelye egybeesik, akkor egy csavarodó, a végtelenségig nyúló egyenest kapunk. Ez kétféle lehet: balos és jobbos, mert egyszerű megfordítással a kapott kombinációk nem vihetők át egymásba. Az előre-balos, előre-jobbos, hátra-balos, hátra-jobbos lehetőségek párokba állíthatók: az előre-balos egyenlő a hátra-jobbossal, az előre-jobbos pedig a hátra-balossal.
Ötödik megjegyzés: Mindebből az is következik, hogy a Bindu, mint a Ponttal topológiailag egyenértékű, egyoldalú felület csak akkor lesz kétféle, ha az időben elkezdjük mozgatni, mindkét módszerrel egyszerre. Az álló, időtlen (statikus) Binduból csak egyféle van. Az időben létező, mozgó (dinamikus), valódi Binduból pedig kétféle (balos és jobbos). A mozgást egy harmadik pont szemszögéből tudjuk csak értelmezni, kívülről nézve.
Hatodik megjegyzés: A körkörös forgás és az egyenes vonalú mozgás tehát együtt, egyszerre jelentkezik az időben, vagyis elválaszthatatlanok egymástól (a természetes valódi terek esetén). Évekkel ezelőtt, amikor az Istent médiumon keresztül kérdeztük a jelenpontról, ezt a rejtélyes választ kaptuk.: "Ha a Bindu nem forog, akkor nem is halad." Most végre érthetővé és indokolttá vált, miért. A fenti levezetés egyben azt is jelenti, hogy a létezés alapja nem a Pont (a szubjektum, a puszta vanás), hanem az egyenes és a kör, vagyis az eltolás és a forgatás (a folyamat). A pont csupán látszólag alapvető, mivel belső struktúrája, szerkezete van (Bindu), amely az időbeli létét (folyamatosságát) adja.
Ha a Ponton alkalmazott forgatás és eltolás tengelye nem esik egybe, vagyis egymásra merőlegesek, akkor egy végtelenségig nyúló, körbe csavarodó, kifelé terjedő, kör alakú síklapot kapunk. Ebből csak egyféle lehetséges, mert a balra és jobbra csavarodó síkok 180 fokos elforgatással fedésbe hozhatók egymással, tehát formailag azonosak. Belülről nézve ez egyoldalúnak mutatkozik, mert az alkotó pontjai maguk is csak egy oldalúak. Kívülről nézve ugyan kétoldalúnak látszik a síklap, de nincs senki, aki kívülről szemlélhetné ezt a jelenséget (a hermetikus létezés belső, szubjektív idejét). Így megkaptuk az egyoldalú, végtelen, valódi 2D-s síkot, a síkszerű univerzumot (idősíkot, falvédőt, rajzlapot).
Most nézzük meg, mi történik a Ponttal, ha csak elforgatást alkalmazunk rajta, de kétszer, két különböző tengely mentén. Ekkor egy kettős forgású időpontot kapunk, ami továbbra is 0D-snek látszik. Ez egy másféle leképzésben egyenlő azzal, ha csak eltolást hajtunk végre a Ponton, de kétszer, két különböző tengely mentén. Ekkor egy egyoldalú, a végtelenségig nyúló kör alakú síkot kapunk (hagyományos polárkoordináta-rendszert), ami 2D-snek látszik, de valójában nem az. Hiányzik belőle a forgás dinamizmusa, vagyis statikus és topológiailag egyoldalú. A komplex számok ettől függetlenül mégis ábrázolhatók rajta (a Gauss-féle számsík).
Ha a Pontot három tengely körül forgatjuk el, ugyancsak 0D-snek látszó, hármas forgású időpontot kapunk. Ezzel egyenértékű a másik leképzése, a Pont három irányú eltolása, ami az ábrázolástól függően létrehozza az euklideszi teret, (az XYZ koordináta-rendszert) vagy az időbeli mozgást is tartalmazó, mindhárom irányba nyúló, növekvő, felfúvódó Minkowski térre hasonlító képződményt. A gond csak az, hogy ez még teljesen statikus, és ezért ál 3D-s, ráadásul egyoldalú (csak külső felülete van, belseje nincs).
Hetedik megjegyzés: Mindezekből jól látszik, hogy a forgás dimenziója nélkül nem lehet igazi, használható teret létrehozni, amiben leírhatók, ábrázolhatók a valódi világ alkotói (tér, fény, anyag, lélek, stb.). A korábbi matematikai modellekből nagyvonalúan kifelejtették a forgást, ahogy a fizika sem tud elszámolni az univerzumban megfigyelhető forgásjelenségekkel. Vajon mitől forognak a részecskék? A bolygók, csillagok, galaxisok? És miért van erős aszimmetria a kétféle forgásirány között? Nem ugyanannyi anyag és égitest forog balra, mint jobbra ugyanis! Az időmatematikai modellben automatikusan adódik a megoldás: a forgás kezdettől ott van minden rendszerben, elidegeníthetetlen alkotóelemként. Az aszimmetria pedig a kiindulási létező (Bindu) forgásirányának következménye, mert minden időbeli másolata az Ő tulajdonságait fogja magán hordozni.

8. TÉRBELI ALAKZATOK - HÁROM DIMENZIÓBAN

A következő lépésben a valódi 2D-s (egyoldalú) síkunkon alkalmazzunk újabb műveletet (elsőnek megint forgatást). Ha ezt a síkot úgy forgatjuk el, hogy a forgástengely a sík dimenzióján belül van (rajta fekszik a síkon, azaz az egyik eltolási tengelyen), akkor egy 3D-s, a végtelenségig nyúló, terjedő, gömbszerűen felfúvódó, kettős csavarodási tulajdonságot mutató teret kapunk. Ez formailag hasonló a Minkowski-féle téridőhöz, de valójában annál sokkal jobb, mert dinamikus, forog, és ráadásul kétféle van belőle: balos és jobbos. Elvileg négyfélének kellene lennie a két forgástengely miatt, de ezek párba állítva egymással egyformák, ezért lényegében csak két fajta létezik belőlük (mint a Binduból). Ilyen tere van fizikailag az emanációs sebességgel mozgó időforrásnak (RV=1 tardion, VÍZ), némi egyszerűsítéssel ábrázolva.
Ha a második forgástengely a sík dimenzióján kívül fekszik, akkor egybeesik az első forgástengellyel, tehát ez a megoldás nem ad új struktúrát a számunkra.
Nyolcadik megjegyzés: Ha a felhasznált 2D-s síkot nem egy elforgatással és egy eltolással kaptuk, hanem két eltolással, akkor szintén egy 2D-s spirális síkot kapunk a dimenzión kívüli elforgatással. De létezik ennek egy olyan leképzése is, ami a természetes képzetes terek csoportjába tartozik: a négyzetes spirál. (10. ábra) Ha az elforgatás mindig csak negyedakkora, mint az eltolás (90 foknyi), és nem egyszerre, hanem felváltva végezzük az eltolást és a forgatást, mindkettőt ábrázolva is, akkor egy négyszögletes spirált kapunk. Ezt csak azért említjük meg itt, mert ősi, az ókor óta ismert szimbólumról van szó, ami értelmében kapcsolódik a svasztikához (négy ágú négyszögletes spirál).


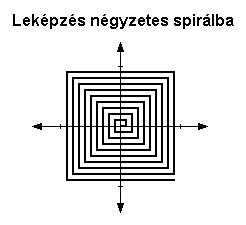
Most próbáljuk meg harmadik műveletként a 2D-s síkon az eltolást alkalmazni. Ha az eltolás tengelye rajta van a síkon, nem alakul ki új struktúra, tehát ez is zsákutcának minősül. Ha viszont kívül van a síkon, tehát arra merőleges, akkor egybeesik a forgástengellyel. Ekkor egy szintén 3D-s, a végtelenségig nyúló, terjedő, felfúvódó, egyes csavarodási tulajdonságot mutató, gömb alakú teret kapunk. Ebből csak egyféle van, mert a balos és jobbos változata 180 fokos elforgatással fedésbe hozható egymással.

9. A NEGYEDIK DIMENZIÓ

A rendszer bővítésének következő lépcsőfoka a kapott két 3D-s modell: a két forgásos és az egy forgásos gömb további mozgatása. Kezdjük a két forgástengelyes gömbök újabb elforgatásával.

9.1. Ha a forgástengely a gömb dimenzióvilágán belül van, akkor nem történik lényeges változás, vagyis egy forgó gömböt kapunk, ami balra vagy jobbra forog. A kétféle gömbből így négyféle 3D-s, hármas csavarodású gömböt kapunk. Egy szemléletes példa erre: a térben is lehet balra és jobbra forogni, meg az antitérben is, de ezek formailag nem párjai egymásnak! Ha a forgástengely a 3D-n kívülre nyúlik, a 4D-be, akkor egy 4D-s spirális hipergömböt fogunk kapni, amely hármas csavarodású. Ebből szintén négyféle van, és ezek sem állíthatók párba egymással.

Ha a 3D-s gömböt úgy toljuk el, hogy az eltolás tengelye a gömb dimenzióvilágán belül van, akkor szintén egy 3D-s (mozgó, tardion típusú) gömböt kapunk (előre vagy hátrafelé mozog). Ha viszont a tengely a 4D irányába mutat, akkor egy 4D-s, kettős csavarodású, a végtelenségig terjedő spirális hipergömböt fogunk kapni, amiből négyfélének kellene lennie, ugyanúgy, mint a hármas csavarodású 4D-s spirális hipergömbből, de mivel ezek egymással szintén párba állíthatók, mint a kettős csavarodású 3D-s gömbterek, ezért csak kétféle van belőle: balos és jobbos. (11. ábra)


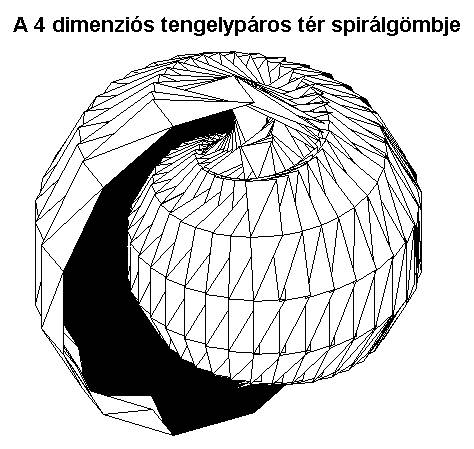
Kilencedik megjegyzés: A 90-es évek elején Kisfaludy György által megalkotott időfizikai világmodell 4D-s téridője hasonló felépítésű, de nem azonos ezzel a két eltolással és két elforgatással képzett, 4D-s, tengelypáros térrel. A Kisfaludy-féle téridő belső idősűrűsége ugyanis kettős az azt generáló tachionok miatt, míg a tengelypáros térben mindenhol egyszeres az idő sűrűsége. Ráadásul nála a hullámtér hat párhuzamosan egymásba ágyazódó, önálló forráshelyű spirálgömbből tevődik össze. A mi tengelypáros terünk ennél lényegesen egyszerűbb, mivel a keltésének gyakorlati oldalával itt nem foglalkozunk. Erről A tér fizikai szerkezete című írásban lesz szó részletesen. Ettől függetlenül kétségtelen az összefüggés a két térszerkezet között. Azt, hogy hogyan (a jelenpont mozgatásának milyen leképzése esetén) jön létre a Kisfaludy-féle téridő a tengelypáros térből, lásd a 12. fejezetben.

9.2. Most lássuk az egyes forgású 3D-s gömb újabb elforgatásából keletkező alakzatokat! Ekkor két eltolást és két elforgatást alkalmazunk egyszerre, vagyis logikusan ugyanazt kapjuk, mint az előbb. Kétféle 4D-s (tengelypáros) spirális hipergömböt.

Ha viszont a gömböt eltoljuk, egy forgó, hármas eltolású gömböt kapunk, amiből kétféle lehetséges. Ha a dimenzióján belül történik a harmadik eltolás, az szintén 3D-s alakzatot eredményez, egy sima, csavarodó Minkowski teret. Ebből csak egyféle van, mert a balos és jobbos csavarodásúak fedik egymást. Ha a dimenzióján kívülre nyúlik a harmadik eltolási tengely, ennek egy 4D-s változatát kapjuk, amiből szintén egyféle van.

10. A MŰVELETI SZABÁLYOK

Mielőtt tovább építenénk a dimenziókat újabb műveletek hozzáadásával, előbb vizsgáljuk meg az eddigi eredményeinket. A bővítési folyamaton jól látható néhány alapvető törvényszerűség, melyekből megpróbálhatunk következtetéseket levonni a magasabb dimenziószámú geometriai struktúrák formájára és tulajdonságaira vonatkozóan.

10.1. Ha az eltolás tengelye a bővítéskor a kiindulási rendszer dimenzióin belülre esik, akkor:
0D-nél: nincs változás. (leképzéstől függően bővülhet 1D-sre is!).
1D-nél: nincs változás.
2D-nél: nincs változás.
3D-nél: nincs változás.
4D-nél: nincs változás.
5D-nél: nincs változás.
6D-nél: nincs változás.
Az ilyen irányú eltolások nem növelik a dimenziószámot.

10.2. Ha az eltolás tengelye a bővítéskor a kiindulási rendszer dimenzióin kívülre esik, akkor:
0D-nél: 1D-s lesz a kapott alakzat.
1D-nél: 2D-s lesz a kapott alakzat.
2D-nél: 3D-s lesz a kapott alakzat.
3D-nél: 4D-s lesz a kapott alakzat.
4D-nél: 5D-s lesz a kapott alakzat.
5D-nél: 6D-s lesz a kapott alakzat.
6D-nél: 7D-s lesz a kapott alakzat.
Vagyis minden dimenziószám esetén bővül a rendszer felfelé plusz 1D-vel.

10.3. Ha a forgatás tengelye a bővítéskor a kiindulási rendszer dimenzióin belülre esik, akkor:
0D-nél: 1D-s lesz a kapott alakzat (leképzéstől függően maradhat 0D-s is!).
1D-nél: nincs változás.
2D-nél: 3D-s lesz a kapott alakzat.
3D-nél: nincs változás.
4D-nél: 5D-s lesz a kapott alakzat.
5D-nél: nincs változás.
6D-nél: 7D-s lesz a kapott alakzat.
Vagyis csak páros dimenziószám esetén bővül a rendszer felfelé +1D-vel.

Ha a 0D-s Pont dimenziószámát páros számnak tekintjük, a forgatáskor bővül a rendszer. Ez fordítva is igaz: mivel a 3. fejezetben (A kör és az egyenes kapcsolata) már részletesen kifejtettük, és indokoltuk, hogy a Pont elforgatása egyenértékű az eltolásával, ezért a nullát az időgeometriai számegyenesen páros számnak kell tekintenünk! Emlékezzünk: "Ha a forrás nem forog, akkor nem is halad!"
Tizedik megjegyzés: Ebből következően a végtelennek is páros számnak kellene lennie, mivel a számkörön a párja is az, a nulla! Viszont ha abból a szempontból nézzük a számkört, hogy azonos mennyiségű páros és páratlan számot tartalmaz, akkor a végtelennek páratlannak kell lennie. A nyilvánvaló ellentmondás feloldásával az Elmélkedések a végtelenről című írásban foglalkozunk.

10.4. Ha a forgatás tengelye a bővítéskor a kiindulási rendszer dimenzióin kívülre esik, akkor:
0D-nél: nincs változás.
1D-nél: 2D-s lesz a kapott alakzat.
2D-nél: nincs változás.
3D-nél: 4D-s lesz a kapott alakzat.
4D-nél: nincs változás.
5D-nél: 6D-s lesz a kapott alakzat.
6D-nél: nincs változás.
Ez pont ellenkezője a 10.3.-as műveleti sorozatnak. Vagyis csak páratlan dimenziószám esetén bővül a rendszer felfelé plusz 1D-vel.

10.5. A forgástengelyek száma a meghatározó a különféle terek darabszámát illetően, a következőképpen.:
1 elforgatás: 2 féle tér, de 1 pár.
2 elforgatás: 4 féle tér, de 2 pár.
3 elforgatás: 8 féle tér, de 4 pár.
4 elforgatás: 16 féle tér, de 8 pár.

Adott forgástengelyszám esetén a kapott terek darabszáma független a tér dimenziószámától, tehát pl.: egy elforgatásos térből 1D-ben, 2D-ben, 3D-ben és 4D-ben is csak egy pár van adott számú eltolási tengely esetén. Ezért lehet a 3D-ben két fajta olyan spirális gömb (2 és 3 eltolásos) is, amiből csak kétféle forgásirányú van. A párba állítható terek a szimmetriájuk miatt egyformák, vagyis egymásba átforgathatók.

11. A MŰVELETI LISTA

A természetes valódi terek csoportján belül a mozgatások során eddig kapott geometriai alakzatok dimenziószáma, elnevezése és fajtái, valamint a rajtuk végzett műveletek összefoglaló listája a következő.:

0D-s pont: n irányú forgatás (n féle, leképzéstől függően).
1D-s álló egyenes: 1 eltolás (1 féle).
1D-s csavarodó egyenes: 1 eltolás, 1 forgatás (2 féle, 1 pár, balos és jobbos, ezek a tengelypáros időszálak).
2D-s spirális sík: 1 eltolás, 1 forgatás (2 féle, 1 pár, egyoldalú).
3D-s spirális gömb: 1 eltolás, 2 forgatás (4 féle, 2 pár, balosak és jobbosak).
3D-s spirális gömb: 2 eltolás, 1 forgatás (2 féle, 1 pár).
3D-s spirális gömb: 3 eltolás, 1 forgatás (2 féle, 1 pár).
3D-s spirális gömb: 1 eltolás, 3 forgatás (8 féle, 4 pár).
4D-s spirális hipergömb: 1 eltolás, 3 forgatás (8 féle, 4 pár).
4D-s spirális hipergömb: 2 eltolás, 2 forgatás (4 féle, 2 pár, ezek a tengelypáros terek).
4D-s spirális hipergömb: 3 eltolás, 1 forgatás (2 féle, 1 pár).

12. A TENGELYPÁROS TÉR AZ IDŐFIZIKÁBAN

Az időfizikai teremtésmodellben a jelenpont gömbszerű időhullámai a kiáradásuk közben minden más jelenpontot tolni kezdenek maguk előtt. Az emanáció taszítása sugárirányban történik. Ez megfelel a matematikában a "normálisnak", ami egy érintőre vagy érintő síkra az érintési pontban emelt merőleges egyenes. A normális a magyar nyelvben többféle jelentéssel bír: szabályos, rendes, elfogadott, megszokott, átlagos, természetszerű, természetes, egészséges, épeszű, józan. A sugárirányú taszításról tehát elmondhatjuk, hogy normális, megszokott dolog a teremtésben. Az emanáció tangenciális, oldalirányú sodrása érintőirányú, erre merőleges, és a hatás mértékét illetően valóban csupán érintőleges, vagyis másodlagos.
Az időfizika térforrásának (térszerán, Mindenható, a téridő keltője) hullámtere időgeometriailag indokolhatóan 4D-s. Ez a spirálgömbi hipertér (túltér), amit egy körpályán mozgó tachion áraszt magából, és amiből a virtuális másolatok felvillanása miatt 5+1 darab van a térkvantumban, szintén két eltolás és két elforgatás következtében alakul ki.
Ebből egy eltolás a jelenpont egyenes vonalú mozgásából adódik (a taszítás miatt), ami ugyan gyorsabb a saját emanációjánál, de pontosan ezért lesz kettős belső idősűrűségű a spiráltere a későbbiekben. További egy eltolás megfelel a saját időhullámai sugárirányú mozgásának, kiterjedésének. Egy forgatás az időhullám rétegek egymáshoz képesti elfordulásából, az érintőirányú sodrásból adódik. A másik elforgatás pedig a tachion körbekanyarodása lesz a ciklikus másolódási rendszerében. Mivel pedig kétféle tachion kúpból (vagy az időgeometriában 3D-s gömbből!) lehet ezt megcsinálni, ezért értelemszerűen kétféle spirálgömb lehetséges. Ezek a tér és az antitér az időfizikában.
Az érdekesség kedvéért még megemlítjük, hogy a térkvantum forráshelyei egy gömbbe írható oktaéder csúcspontjain helyezkednek el egymáshoz képest. Az időgeometriában pontosan ugyanezt kapjuk, ha a 3 eltolással és 1 elforgatással képzett, 4D-s spirális hipergömb jelenpontjait kötjük össze egyenesekkel a 4.1.3.-as leképzési módszer szerint. A nyilvánvaló összefüggés (formai azonosság) indoka az, hogy a 3 eltolásos és 1 elforgatásos spirálgömbünk megfelel a Kisfaludy-féle téridő azon leképzésének, amelynél az érintőirányú sodrást nem elforgatásként, hanem oldalirányú eltolásként (vektorként) értelmezzük.
A térszorzással képzett paralel térhatosok (hipertérhatosok) szerkezetével és mindezek jövőtereivel most nem foglalkozunk, mert ezek logikusan következnek a meglévő rendszer kiterjesztéséből. Legalább hagyunk valami feladatot az utánunk jövő kutatóknak is.

13. TOVÁBBI MEGJEGYZÉSEK


Ha a világunk (a teremtés) működése több, mint 3D-ben zajlik, akkor azt a 3D-ből szemlélve nem lehet sem tisztán átlátni, megérteni, sem a törvényeit, tulajdonságait lekonvertálni 3D-s világmodellé információ vesztés és paradoxonok megjelenése nélkül. Ez a magasabb dimenziószinteken is igaz lesz. Ebből viszont az következik, hogy gyakorlatilag csak Egy valaki van, aki átlátja a minden létezőt: önmaga, az n-1D-s rendszer. Őróla tudjuk, hogy intelligens és minden létező tudással rendelkezik önmagáról (az Isten). Az egész egyes részei, vetületei számára tehát gyakorlatilag megfejthetetlen titok marad a teljes létezés örökre, bár elvileg következtethetünk az alsóbb dimenziószinteken megfigyelt szabályok (természeti törvények) alapján a tágabb valóságra.
A dimenziószám növelésekor jól látható, hogy minden szinten megjelennek olyan új formai lehetőségek, melyek nem következnek az előző dimenzióból, pusztán az ottani alakzatok egyszerű bővítésével. Ahhoz, hogy létrehozhassuk őket, kívülről információt kell bevinnünk a rendszerbe, megadva az alakzat konkrét paramétereit. Ilyen pl.: 1D-ben: a véges szakasz (milyen hosszú legyen?). 2D-ben: az üres kör (karika) és az üres négyzet (mekkora legyen?). 3D-ben: az üres kocka és egyéb, bonyolultabb alakzatok. A 4D-s alakzatokról csupán sejtéseink vannak. Az, hogy ez a bővülés, az információ tartalom növekedése hogyan és miért történik, későbbi (informetriai) kutatási témánk lesz majd.

14. FELMERÜLŐ KÉRDÉSEK

Az eddigiek számos érdekes kérdést vonnak maguk után. Ezek közül a legfontosabbak a következők.:

14.1. Hol van a határa, és van-e egyáltalán korlátja a dimenziók bővítésének?
Elvileg elképzelhetők potenciálisan végtelen kiterjedésű (n dimenziós) terek, a képzési szabályok további alkalmazásával, de a gyakorlatban nem tudjuk, hogy megvalósíthatók-e. Az időfizikában egy időforrás 1D-s időszálának térré fejlesztéséhez más időforrások taszító, sodró hatásaira van szükség. Ha minden elmozdulást egy dimenziónak veszünk, akkor minden forrás hullámtere annyi dimenziós lesz, ahány időhullám éppen eléri és perturbálja a saját mozgását, szitálását a minden létező eseményterében. Ezen időhullámok száma azonban kevesebb (n-1)-nél, aminek okait részletesen kifejtve lásd: Az időhullámok hatásai című írás első fejezetében.

14.2. Van-e értelme számunkra kutatni a 4D-snél bonyolultabb, magasabb szintű tereket a gyakorlati használhatóság szempontjából?
Mivel a különböző dimenziószintek az 5.6. fejezetben meghatározott módon váltakoznak az időgeometriai modellünkben, matematikailag nincs felső korlátja a téridő dimenziószámának. A Kisfaludy-féle időfizikai modellben a téridő dimenziólépcsője 0-tól 6D-ig terjed fölfelé (ez nem azonos a térhatos-hipertérhatos közti átvonulási dimenziólépcsővel!). Mi viszont elsősorban csak a saját szintünket és az alattunk lévőket látjuk (pontosabban az alsóbbakat sem). A 4D-s téridő tulajdonságainak kutatása biztosan szolgál majd olyan gyakorlati eredményekkel, mint pl.: a három dimenziós mozgás felgyorsítása térugrás segítségével vagy az olyan parajelenségek megértése, mint a gömbvillám, a távolba látás és a Fülöp-szigeteken népszerű csodadoktorok "testbe nyúlós" pszichosebészete.

14.3. Milyen fajtájú egymásba ágyazott, párhuzamos terek létezhetnek?
A párhuzamosan egzisztáló, tehát helyileg egymásban felfúvódó spirálgömbök lehetnek egyenrangúak, mint a térforrás 5 forrásának spirálterei vagy alárendeltek, mint az ebben (a domináns térben) születő további, későbbi alterek (a fénykvantumok terei).

14.4. Milyen eredő geometriát hoznak létre az önálló forrásrendszerű, egymással egyenrangú terek, amikor egymásba hatolnak?
Két külön térforrás spirálgömbi terének találkozása magukat a tereket nem fogja érinteni, megváltoztatni, viszont azok kölcsönösen hatni fognak a másik tér keltő forrására (annak jelenpontjaira) és minden más altérre, ami beléjük kerül (együttesen).

14.5. A mi anyagi világunk, amiben élünk (a Föld, a Naprendszer), vajon melyik spirálgömb lehet a sok lehetőség közül? Hány dimenziós a világunk valójában (amit látunk magunk körül)?
A fizikusok és az átlagemberek a mai napig esküsznek rá, hogy a világunk három dimenziós és az euklideszi térre hivatkoznak teljesen jogosan. A Kisfaludy-féle modellben az anyagi világ a 4D-s téridő egyik 3D-s vetülete, vagyis az egész Naprendszer egy olyan "térbuborékban", altérben foglal helyet az univerzumban, amelyen kívül 4D van, belül viszont csak 3D. Az időgeometriai modellben csak egy olyan leképzés van, amelyik mindkét állításnak megfelel, éspedig a 9.1.-es pontban említett 3D-s, egy eltolásból és két csavarodásból felépülő spirálgömb, amiből négyféle van: balos és jobbos, a térben és az antitérben. Valószínűleg tehát ehhez hasonlít, de nem pont ilyen a mi terünk matematikailag.

14.6. A mi világunk 3D-s térszerkezete vajon balra vagy jobbra forgó?
Ezt már nem olyan könnyű egyértelműen eldönteni, mert mindkét lehetőségre találhatunk példákat a természetben. Az óramutatók járása, forgási iránya (a mi időterünk forgása!) például jobbos, akárcsak a csavarodó csigaházak elsöprő többsége, mintha ezek az állatok kimondottan a térrel szinkronban növesztenék a meszes héjukat. A csavarmeneteinket is többnyire jobbosra készítjük (de nem mindig, mert a fordított irány nagyon jól használható bizonyos célokra) és az emberek többsége jobb kezes minden társadalomban.
Ugyanakkor az összes stabilan megmaradó anyagi részecskéről tudjuk (neutron, proton, elektron), hogy balra forog a tengelye körül, akárcsak a sejtekben található DNS lánc vagy a Naprendszer bolygóinak elsöprő többsége (a Nap is balra forog, míg a Vénusz és az Uránusz jobbra).
A keresztény vallásban a Teremtő Atya Fia, Jézus Krisztus a mennyben az Atya jobbján ül a trónusnál. Az Atya (Úr, férfi Isten) nyelvtanilag hímnemű, s ennek megfelelően a férfiak ruházata jobbra gombolódik, a nőké pedig balra. A magyar nyelvben mindig a jobbos irány a jobbik (lásd: jószerencse, balszerencse, jobbulás, baleset, stb). A hindu vallásban elterjedt svasztikának, a forgó négyágú spirálnak két változata van: a jobbra csavarodó az élet jele, a balra csavarodó (horogkereszt) a halálé. Az ókori régészeti leletek (épületmaradványok, edények) között sok helyen megtalálhatók balos és jobbos spirálok rajzai, kerek és szögletes változatban egyaránt (hinduknál, keltáknál, indiánoknál, stb.). Ezek jelentése többnyire az energiával vagy az élettel és a halállal kapcsolatos.
Összevetve az érveket és ellenérveket, valószínűnek látszik, hogy a mi terünk jobbos csavarodású, amiben az anyagi rendszerek valamiért balra forognak. Az antianyag, amely jobbra forgó, nem képes stabilan megmaradni a mi terünkben, még akkor sem, ha elkülönítjük a balos anyagi részecskéktől. Ennek a jelenségnek a fizikai okaival más írásokban foglalkozunk.

15. TÁVLATI KÖVETKEZMÉNYEK

Ez az egyesített térgeometriai rendszer az összes korábbi térszerkezetet magába foglalja (Euklidesz, Bolyai, Riemann, Kisfaludy), és logikus magyarázatot ad azok létére, valamint feltárja a különféle terek és leképzések közti összefüggéseket. Általa végre számítógépen is pontosan modellezhetővé és ábrázolhatóvá válnak a valódi dimenziók, ami több tudományos kutatási terület számára nagy segítséget fog jelenteni.
Az emberi agy számára komoly gondot jelent, hogy sem önállóan, sem a számítógép segítségével nem képes praktikusan dolgozni egy n idődimenziós gömbbel vagy egy 3 térdimenziósnál nagyobb kiterjedési számú objektummal. Nem kezelhető valós időben (vagy akár emberileg elfogadható időtartam alatt) matematikailag egy sok milliárd idődimenziós fizikai objektum, annak bonyolultsága okán. Ezen a helyzeten a nagy teljesítményű kvantum számítógépek is csak javítani fognak némiképp, de semmiképpen sem oldják meg a problémát. Elsősorban ennek a nehézségnek köszönhető, hogy a tudományban a mai napig megmaradhatott az a téves elképzelés, miszerint a tér szerkezete egyszerűen megfelel az XYZ koordináta-rendszernek, mert abban könnyű számolni és gondolkodni. Az igazság azonban az, hogy csak azért, mert a 3D-s térben elhelyezhető az XYZ rendszer, az még nem jelenti azt, hogy a tér fizikai szerkezete azonos ezzel a matematikai konstrukcióval.
Ha a tudósoknak végre sikerül tovább lépniük ezen az akadályon, akkor kezdődik csak el igazán a téridő tudományos kutatása. A valódi három dimenziós televízió (holovízió) működése, az anyagi részecskék szerkezete és időbeli mozgása, valamint a kölcsönhatásaik végre szimulálhatóvá válnak, akárcsak az elektromágneses terek tulajdonságai, térbeli formája. Legfőképpen pedig a tér ismerete hozzásegíthet bennünket ahhoz, hogy megértsük a bolygónk légterében régóta száguldozó földönkívüli űrhajók meghajtórendszereinek működési alapelveit. A zárt inerciarendszerű meghajtást, amit közönséges nyelven csak antigravitációnak hívnak, továbbá a térugrást, a magasabb dimenziószinteken keresztül történő (3D-s mozgás nélküli) helyváltoztatást. Ezekkel a témákkal részletesen más írásokban foglalkozunk.
Mindezen következmények miatt az időmatematika alighanem a XXI. század legfontosabb tudományágainak egyike lesz majd, és remélhetőleg az emberileg gyors csillagközi űrutazás lehetőségét is a kezünkbe adja néhány évtizeden belül.

Készült: Békéscsaba, 2002.09.28. - 2007.05.03.

Következő írás

Vissza a tartalomhoz