1. ÉRZÉKELÉS A TÉRBEN
Minden élőlény számára létfontosságú, hogy az érzékszerveivel képes legyen pontosan észlelni a határai körül zajló eseményeket. Ezáltal tudja megtalálni a táplálékát, elkerülni a veszélyeket és tájékozódni a környezetében. Az időtopológiai publikációkból tudjuk, hogy az n dimenziós véges objektumoknak n-1D-s határa van. Ha az objektumokat élőlényeknek tekintjük, akkor logikusnak tűnik, hogy n dimenziós beágyazási környezetben az érzékelő rendszereik a határfelületükön fognak koncentrálódni, vagyis lokálisan n-1 dimenziósak lesznek. Ennek megfelelően az érzékszervek n-1D-s leképzéssel fogják fel a beérkező információkat és továbbítják azt az idegrendszernek.
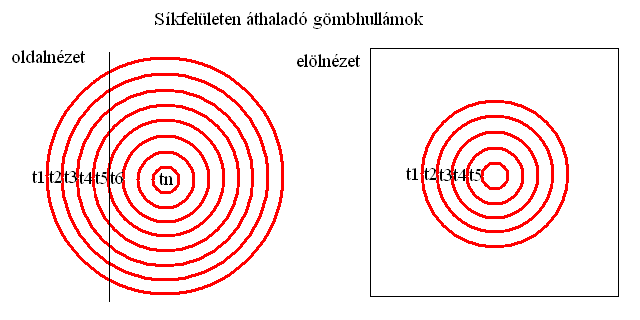
A 3D-s ember szemében a látóidegsejtek egy felületen helyezkednek el, vagyis kvázi 2D-ben fogják fel a fényt. Ahogy a fényképezőgépbe helyezett film is egy vékony síklap, melyre leképeződik a térbeli látvány vetülete. A két szem teszi lehetővé a sztereoszkopikus látást az információ utófeldolgozása révén, ezért tudunk a sík képet látó szemeinkkel térben tájékozódni. Ugyanígy a füleink is csak a hanghullámok egy vékony, síkszerű szeletét érzékelik egyszerre. A hangok időbeli változásából, valamint a két fül által érzékelt rezgések késedelmi idejéből tudjuk kiszámítani a forrás irányát és távolságát. A bőrünk szintén kvázi síkfelület, amely a környezettel való érintkezés során szolgáltatja a tapintás élményét, ahogy az orrunk szaglószőrei találkoznak a belélegzett molekulákkal vagy a nyelvünk ízlelőbimbói a táplálékkal. Még a belső fülben található egyensúlyozó szervünk kör alakú járatai is kvázi síkban működnek, igaz ezekből három darab van és egymásra mind merőlegesek. Mivel a 3D-s térben három egymásra merőleges síkot lehet elhelyezni egy közös metszésponttal.
Ha a szemfenék látóidegsejtjei egy egyenes síkban helyezkednének el, akkor a rá beérkező fényhullámok gömbfelületei középről kiindulva metszenék azt, egyre táguló körökben szaladva szét a felszínén. Mivel azonban a szem gömbölyű, a szemfenék egy homorú felület lesz, aminek van egy gyújtópontja. Így az ennél messzebbről érkező hullámok alacsonyabb görbültségű rétegei épp ellenkezőleg metszik a szemfeneket, először a szélét érve el, majd körgyűrűszerűen összeszaladnak középre, egyetlen pontba. Ez a pont a látásunk fókusza, ahol a legélesebb a kép, míg körülötte található a periférikus látás területe. A probléma elkerülésére fókuszálja a fényt a szemlencse egyetlen szűk nyalábba, pontosan az érzékelő felülethez igazítva azt. Ezen nyalábon belül a fénykvantumok mégis gömbhullámszerűen szétterülő alakzatban repülnek keresztül a szemen és a szemfenék különböző pontjaira becsapódva eltérő hosszúságú utakat járnak be a térben.
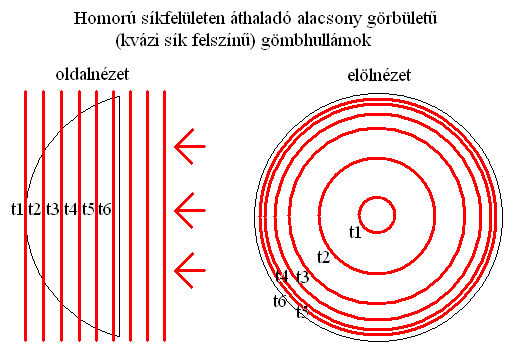
Ebből következik, hogy a szemünkkel nem egyetlen (eszményien vékony) időpillanatot látunk (az időegyenesből), hanem annyit (olyan vastag szakaszt), ahány hullámréteg egyszerre metszi a homorú felületet. Még akkor is, ha csak egyetlen pontból érkezik szemünkbe a fény és nem különböző futási (és ezért időbeli) távolságra lévő tárgyakról verődik össze. A fény terjedési sebessége persze olyan nagy, hogy a hozzá képest jóval lassúbb reakcióidejű látósejtjeinkkel és idegrendszerünkkel képtelenek vagyunk érzékelni ezt az apró időbeli elmosódottságot.
Erről azért érdemes tudni, mert a jelenség fizikai alapelve nagyon jól hasznosítható lesz például a gravitációs érzékelők fejlesztésénél, ahol van jelentősége az időbeli futási késedelemnek. Gondolunk itt például arra a problémára, ami már az egyszerű optikai mikroszkópoknál is jelentkezik és nagyítási korlátként ismert. A túl apró dolgok azért nem láthatók lencsés mikroszkóppal, mert nem lehet a képet élesre állítani. A tárgyról visszaverődő fényhullámok futási útvonala ugyanis nagyon eltérő hosszúságú a lencse közepe és széle között, így időben széthúzott képet kapunk, amit még jobban elhomályosítanak a tárgy apró rezdülései, elmozdulásai például a molekulák, atomok szintjén. Ha nagy felbontású gravitációs mikroszkópot akarunk készíteni, az érzékelőket a tárgyból kiáradó gömbhullámok felülete mentén kell majd elhelyezni, hogy ezt a hatást kiküszöbölhessük.
De most inkább térjünk vissza az n dimenziós élőlények érzékelésére, mert itt még sok érdekes jelenség vár felfedezésre. Először vizsgáljuk meg az alsóbb szintek lényeit (1D-ben és 2D-ben), majd próbáljuk meg kitalálni, mit és hogyan láthatnak a magasabb szinteken élők (4D-ben).
2. ÉRZÉKELÉS ALACSONYABB DIMENZIÓKBAN
A fenti logika alapján a síkuniverzumban lakó 2D-s élőlényeknek az érzékszervei 1D-s szakaszok lesznek, egyenes vagy ívelt (homorú, domború) alakúak. Az ezt elérő síkhullámok felszínei, szálszerű körvonalai 1D-s érzékelést tesznek lehetővé a számukra. Ez nem tűnik túl informatívnak, de azért lehetőséget ad az irány és távolság meghatározására, mint a 3D-ben a két szem együttes képe.
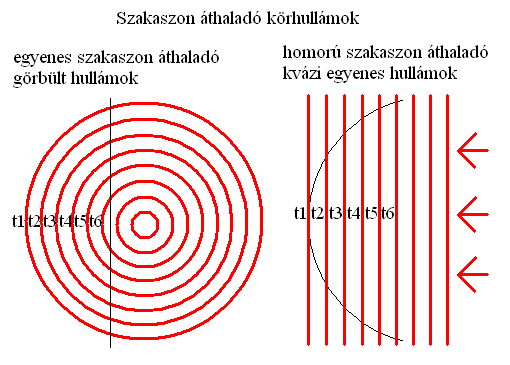
Egy egyenes szakasz formájú szemet csak akkor metszenek a távolból érkező, és ezért alacsony görbültségű hullámkörök a teljes felülete mentén egyszerre, ha pontosan az oldalát mutatja a forrásuknak (vagyis merőleges a normálvektorukra). Ha a szem szakasza nem párhuzamos a kvázi egyenes hullámkörökkel, akkor az érkezési irányból fognak végigfutni rajta a körök, tehát a látott kép időben eltorzul, szétcsúszik a két végpont között. Ha a szakasz szem homorú, akkor a két szélén jelenik meg egyszerre egy időpillanat hullámköre, majd ezek összeszaladnak és középen egyesülnek. Ha a szem domború, épp fordítva történik és középről szalad szét a kettészakadó pont, mely egy időpillanatot reprezentál.
A száluniverzumban lakó 1D-s életformák szemei csak kvázi 0D-s pontulatok lesznek, amin az áthaladó 1D-s információs hullámok mindig 0D-s érzékelést tesznek lehetővé. A szakaszlények az egy forrásból eredő eseményhorizontot - ami két egymással ellentétes irányban szétszaladó pontot jelent - csak egy pontnak érzékelik. Több érzékszerv esetében (amikből bőven elég kettő) az irányt is meg tudják határozni (erről vagy arról jön a szálon a futási késedelem miatt), de a távolságot már nem, mert az egyenesen minden pont egy irányban helyezkedik el, egymás takarásában (nincs parallaxis). A pontulatnyi szemek számára tehát a látott kép nem hasad fel, mint a síklény szakasznyi szeme számára, ezért normálisan csak egy időpillanatot észlelhet egyszerre. Ez alól ritka kivételt jelent az a speciális eset, ha a szemlélt objektum éppen emanációs sebességgel közeledik felé, mert a doppler effektus még itt is működik a szál mentén. Nagyon furcsa dolog lehet ilyenkor egy pontban egyszerre sok időpillanatot látnia a szakaszlénynek (időtágulatot lát).
A száluniverzumban élő lények érzékszervei tehát csak a rajtuk áthaladó hullámok (pontok) sűrűségváltozását és időtartam különbségét képesek észlelni, a távolságukat nem. Az egymás mögött elhelyezkedő dolgok képe egymásra szuperponálódik, s emiatt nagyon nehéz bármit is kivenni az általános zajból. Ennek alapján levonhatjuk azt a következtetést, hogy minél magasabb dimenziószinten történik az érzékelés, annál kevésbé zajos a kép és annál tisztábban láthatók a dolgok. Könnyebb elkülöníteni egymástól az egyes objektumokat, mert egyre kevésbé takarják egymást.
Amennyiben a száluniverzum lényei olyan pontokból állnak, melyek nem képesek a környezetük pontjain áthatolni, úgy a mozgásra nem sok lehetőségük van egész életükben. A szakaszlények maximum lökdösődhetnek (ide-oda) ebben a világban, de nem képesek végigmenni a szálon ténylegesen (fizikailag), mert egyszerűen nincs hely az egy pont vastag egyenesen (nem tudják egymást kikerülni). A két pont vastag egyenesen nincs ilyen probléma, feltéve, hogy az útjukba kerülő objektumok nem foglalják el mindkét pontsort a szálon. A ponthullámok viszont simán átmennek mindenen, ahogy hosszirányban végigrezegnek a szálon, tehát az 1D-s univerzumban csak az információ (a pontok állapotváltozása) közlekedik zavartalanul. A hullámok terjedésének fizikájával bővebben a Rezgések n dimenziós közegben című írásunkban foglalkoztunk.
A síkuniverzum lényei már képesek mozogni a világukban, egymás határolóélei mentén elkerülve egymást, ahogy a 3D-ben a tárgyak a határolófelületeik mentén súrlódva vagy csúszva mozdulnak el. Mielőtt azonban tovább lépnénk a magasabb kiterjedések irányába, előbb tennünk kell néhány időfizikai kiegészítést a fenti témákhoz.:
A száluniverzumban való fizikai mozgás nehézségeivel az Életfán föl-alá szaladgáló profi sámánoknak nem árt pontosan tisztában lenniük, mert ilyenkor nem történik valódi közlekedés. Nem a lélek száguld végig a szálon, mint valami vasúti sínen a felsőbb világok irányába és vissza, hanem csak szoftveresen (informatikailag) kapcsolódik át a szálakon keresztül a sámán tudata. Mintha az interneten keresztül lépne be egy virtuális világba, ami egy tőle sok száz vagy ezer kilométerre lévő szerveren fut fizikailag.
Mindebből persze az is következik, hogy ha térkapukat akarunk készíteni, akkor ezek két oldala nem kapcsolható össze párhuzamosított időszálkötegekkel. A nagy távolságra való átlépést tehát más módon kell megvalósítani, de erről majd a térablak technológiát bemutató emanikai írásokban fogunk részletesen írni.
Az őskáoszban szaladó tachion a múltjába visszalépve egy helyről (jelenpont) két külön időpillanatot (múltbeli képet) lát, amik egyszerre haladnak át rajta. A folyamat leképzésétől függően azt is mondhatjuk, hogy a szemlélő áll, az idő és a szemlélt kép pedig mozog. Az eredmény ugyanaz lesz: az idő felhasad a jelen számára és két irányba látszik telni. Emberi szintű hasonlattal élve, mintha valaki pénteken meglátná a kedden és szerdán történteket egyszerre, de oly módon, hogy a szerdai események előrefelé mozognak az időben (csütörtök felé), a keddiek meg hátrafelé (hétfő irányába).
A 3D-s testünk érzékszervei számára, mivel azok kvázi sok pontból állnak (sok érzékelő elemből), pont fordítva történik ez a dolog a téridőben. Egy pont (távoli esemény forrása) adott időpillanatát egyszerre több helyről is látjuk (mert több érzékelő elemünk, szemünk van), miközben az információt hordozó hulláma mozog (átmegy rajtunk). Ez leképezhető úgy, hogy az idő és a szemlélt kép kvázi áll, a szemlélő pedig mozog hozzájuk képest. Itt mozgás alatt most a szemlélő kölcsönhatási felületén (szemén) jelentkező realizáció módját értjük. Egy hullámréteg különböző helyeken érinti az érzékelőket, ahogy áthalad rajtuk.
Amint az látható, itt két, egymást kiegészítő jelenségről van szó, amivel korábban már részletesen foglalkoztunk az Összefüggések az idő és a tér között című írásunkban. Az egyiknél az idő mozog és a tér áll, a másiknál az idő áll és a tér mozog. Ez a leképzés logikailag érdekes kapcsolódási pontot fog a későbbiekben jelenteni a térkapuk és időkapuk működésének modellezéséhez, de ne vágjunk a dolgok elejébe és most maradjunk meg az érzékelés témájánál.
3. ÉRZÉKELÉS MAGASABB DIMENZIÓKBAN
Próbáljuk meg a korábbiak alapján kikövetkeztetni, hogy a 4D-s túlvilágban lakó élőlények érzékszervei hogyan működhetnek. Az nyilvánvaló, hogy az érzékelést végző szerveik nem 2D-s felület mentén, hanem 3D-s térfogatban helyezkednek el. Ezen áthaladva a 4D-s hullámok (fény, hang, szagmolekulák, ízmolekulák, de a tárgyak térfogata is!) a 3D-s határukkal lépnek kapcsolatba, amiből a parallaxis és az időbeli mozgás révén alakul ki a tudatukban a 4D-s túlvilág (hipersztereoszkopikus) képe.
Ha a 4D-s szem fenekén sorakozó látóidegsejtek 3D-s térfogata a 4D-ben nem egyenes, hanem görbe (homorú vagy domború), akkor a beérkező fotinók (vagy ha a gravitációs hullámokat látják: az időhullámok) ugyanúgy, mint a 2D-ben és a 3D-ben, a görbültségüktől függően fognak benne egy időben széthúzott látványt kelteni. Csakhogy ne feledkezzünk meg arról, hogy minden egyes 3D-s hullámréteg számos 2D-s metszetből áll össze, amik valószínűleg egyfajta plusz információt szolgáltathatnak az arra érzékeny szerv számára. Itt arra gondolunk, hogy a 4D-ben nem csak a távolságot és irányt lehet meghatározni két szem segítségével, hanem a dolgok vastagságát is. Ahogy a 3D-ben az irány és távolság alapján a tárgyak felületi jellemzői felismerhetők, például az egyenetlenségek, görbületek, úgy a 4D-ben a hipertestek térfogati jellemzői lesznek felismerhetők. Mintha részben belelátnánk a dolgokba. Persze nem teljesen, mert ahogy a 3D-ben sem látunk bele a 3D-s tárgyakba, úgy a 4D-ben sem a 4D-s tárgyakba, mégis sokkal több információhoz juthatunk róluk látás útján.
Elég nehéz erről írni, mivel a magyar nyelvünk is 3D-s, itteni viszonyokra lett kialakítva (az eredeti 4D-s fogalomnyelv redukálásával), de talán az analógiák némileg segítenek a magasabb kiterjedések viszonyainak megértésében. Más nyelveken ezt megérteni még nehezebb lesz az emberiségnek, mivel ma a Földön a magyar áll szerkezetileg a legközelebb az Isten által alkotott természetes fogalomnyelvhez (ősnyelvhez), amit az égi lények a teremtés kezdetétől a végéig beszélnek szerte a világegyetemben. Ezzel kapcsolatban érdemes utána olvasni Varga Csaba nyelvészeti kutatásainak.
A 4D-ben nyilvánvalóan teljesen mások lesznek a fizikai törvények, mint a 3D-ben, amivel később még sokat foglalkozunk más emanikai írásokban. A 4D-s tárgyak nem csak a felületük, hanem a térfogatuk mentén is elhaladhatnak egymás mellett (csúszva vagy súrlódva), ami a mi szemünkben gyakorlatilag fedést, részleges egymásba hatolást jelent. Ahogyan két 3D-s ember testének 4D-s aurája is minden gond nélkül egymásba tud hatolni kellő közelség esetén (valamint belelóg a talajba, környező tárgyakba, az épületek falába), mégsem okoznak ezzel problémát maguknak. A meditáló szerzetesek által emlegetett misztikus élmények a mindennel való egység állapotáról, az egység érzéséről fizikailag innen (is) erednek. Az illetőnek 4D-s élménye van, amikor testen kívüli kalandozása során az asztráltestével a túltérben mozog, megtapasztalva annak sajátos fizikai viszonyait.
Ha a 3D-ben használt írás 2D-s alakzatokból áll egy kvázisík papírlapon vagy monitoron, akkor a 4D-ben ugyanez 3D-s testek elhelyezését jelenti egy kvázitérbeli papírlapban vagy monitorban. A mi számunkra roppant érdekesen működhet a 4D-s világban a rajzolás, festészet egy térfogatban vagy a szobrászat, ami nem a nyersanyag felületét, hanem térfogatát munkálja meg. A 4D-s civilizációk nyilván alapból 3D-s monitorkockákat használnak, s a házak falait is mindenhol térbeli vastagsággal rendelkező plakátok díszítik.
A dimenziószinteken fölfelé haladva, a magasabb kiterjedések felé azt mondhatjuk, hogy az élőlényeknek egyre tisztább, részletesebb képük van a környező világukról. Ez szükségszerűen a gondolkodásukban is megmutatkozik, valamint a kommunikációjukban (beszéd, gesztusok, telepátia, stb). Érthetőbben megfogalmazva: A száluniverzumban észlelt pontszerű látvány megértése éles elmét és pontos meghatározásokat kíván. A síkuniverzumban élesedni kezd a látvány, bár ehhez még síkagyúak vagyunk. A térben felületes lesz a szemléletünk, s vele a gondolkodásunk és kommunikációnk is, míg a kapcsolatainkban hajlamosak vagyunk elsiklani számos sikamlós dolog felett. A túltérben viszont már tartalmas látvány tárul az arra érdemes megfigyelő elé, ami igencsak teletömi mélyértelmű információkkal az agyunkat.
4. KÖVETKEZTETÉSEK
Az érzékelésnek tehát alapvetően két fajtája van n dimenzióban. Az elsőt nevezhetjük természetes érzékelésnek, ami mindig n-1D-s. Ilyen például a 3D-s ember 2D-s látása, hallása, szaglása, tapintása és ízlelése. Azért ilyen, mert a 3D-s élőlények számára az a praktikus (minimálisan szükséges), ha a környezetükben lévő dolgok megkülönböztetéséhez a határolófelületüket ismerik. Egy antilopnak bőven elég ismernie az oroszlán felszíni jellemzőit ahhoz, hogy messziről észrevegye és elkerülhesse, nem kell megtudnia, mi van a ragadozó testén belül.
A másikat nevezhetjük mesterséges érzékelésnek, aminek célja az nD-s képalkotás a világról. Az intelligens lények képesek eszközöket, műszaki berendezéseket készíteni, amik segítségével az őket érdeklő, de normálisan nem látható dolgokat is megvizsgálhatják. Ilyen például a röntgen televízió, az MMR, az ultrahangos szkenner vagy a gravizor. Ezek képe ma még inkább csak sík képernyőkön jeleníthető meg, de rövidesen el fog jönni a pillanat, amikor a holovízió a térben fog lebegni és körbejárhatjuk, beledughatjuk a fejünket, hogy jobb képünk legyen a valóságunkról.
Az n dimenziós képalkotáshoz szükséges információ aktív vagy passzív módszerekkel nyerhető ki a közegből. Az aktív érzékeléshez azok a transzcendens hullámok vagy részecskesugárzások alkalmasak, melyek áthatolnak a vizsgálni kívánt tárgyakon és közben megváltoznak a tulajdonságaik (ultrahang, infravörös fény, röntgensugárzás, radarhullám, stb). A passzív érzékelés lényege, hogy fel kell fogni a tárgyakból áradó természetes sugárzásokat, a hőt, radioaktivitást, elektromágneses hullámokat vagy a gravitációt. Bármelyik módszert is választjuk, az általa nyerhető kép sokkal nagyobb információtartalmú lesz, mint a határfelület szemléletével kapható. Szerencsére az élőlények tudata még képes ezzel megbírkózni, mivel a saját dimenzióvilágán belül marad a látvány komplexitása. Ugyanez már nem mondható el az n+1D-s látványról, és pontosan ennek köszönhető, hogy a 4D-s túltérrel kapcsolatos emberi élmények leírásai annyira ellentmondásosak és zavarosak.
A 4D-ben a tárgyak érintkezése 3D-s térfogat mentén történik, ami a mi szemszögünkből nézve a dolgok egymásba hatolását jelenti gyakorlatilag. Ha a 3D-ben a 2D-s felület mentén érintkező tárgyak összetapadnak, összeragadnak, súrlódnak, gördülnek és csúsznak egymáson, akkor ennek megfelelően a 4D-ben a 3D-s térfogat mentén érintkező tárgyak (részben) egymásba olvadnak, eggyé válnak, egymásba hatolnak, összekeverednek, feloldódnak. Itt szintén fellép közegellenállás, súrlódás, összenyomódás, feltorlódás, átgördülés, összeragadás és keresztülcsúszás.
Az emberi aura sok egyéb funkciója mellett érzékszervként is működik, mert képes a belehatoló tárgyak, sugárzások, más aurák jelenlétének érzékelésére. Mivel 3D-ben fogja fel a beérkező információkat, logikus, hogy 4D-snek kell lennie. Hisz minden természetes érzékszervünk n-1D-s észlelésre van kitalálva. Az embernek tehát vannak magasabb dimenziókban működő érzékszervei is, csak ezek használatáról le vagyunk nevelve (szoktatva) születésünktől kezdve. Ez a síkagyú civilizációnk beszűkült, felületes gondolkodásának következménye, ami hatékonyan elzár minket a tágabb világegyetem megismerésétől. Így aztán nem csoda, hogy csak keveseknek adatik meg a megvilágosodás élménye, az igazi rálátás a környező valóságra. Ehhez már önismeretre, pontosabban lélekismeretre van szükség, amivel a következő fejezetben foglalkozunk.
5. ÉRZÉKELÉS LÉLEKKEL
Ha az emberi agy képes a 3D-s világ jelenségeit egymással összehasonlítani, asszociatív kapcsolatok kialakítása céljából, akkor ennek a folyamatnak szükségszerűen 4D-ben kell történnie fizikailag, mert csak a négy változós kiterjedésben lehet 3D-s objektumokat teljesen fedésbe hozni. Az asszociáció lényege ugyanis éppen az, hogy két dolgot pontról pontra összehasonlítunk, megállapítva a közös és eltérő vonásaikat. A pontok pedig a 3D-s tárgyaknak nem csak a 2D-s felszínén, hanem a belsejében is ott vannak, míg a közös vonások olyan egyenesek, szakaszok lesznek, amik ezen pontokat összekötik az adott objektumban. Ezen vonások összessége alkotja a tárgy formai vázát, lásd A forma, a felület és a tartalom című írást.
Ha valaki számára esetleg nem lenne elég világos, mire gondolunk, akkor jusson eszébe, hogy két 2D-s képet is csak 3D-ben lehet pontról pontra összehasonlítani azáltal, hogy egymásra helyezzük őket. Ha a képek háttere átlátszó, rendkívül könnyű eldönteni (a térből nézve), azonos-e a két ábra vagy sem. A felülről történő rálátás gyors belátással jár. Egymás mellé téve őket a síkban ez sokkal komplikáltabb feladat lenne bármilyen szemlélő számára, főleg nagy bonyolultságú ábrák esetén. Most már talán érthető az Olvasó számára, miért működnek a holografikus asszociatív memóriák hihetetlen gyorsasággal. A lelkek számára a formai különbségeket felismerni csak egy pillanat kérdése, minden megerőltetés nélkül.
Mivel pedig a 3D-s fizikai testben működő 3D-s agyszövet nyilvánvalóan nem alkalmas a 4D-s információk kezelésére, tárolására és feldolgozására, arra a következtetésre kell jutnunk, hogy az ember nem az agyával gondolkodik. Ez pontosan egybevág a korábbi lélektani kutatásaink eredményeivel, mely szerint a lelkünkkel gondolkodunk. A lélekbarion óriásrészecskéje pedig (ami a talamuszba ágyazódik be) 4D-s. Mármint a feltudati része, mert a tudatalattija (lélekszentély) meg 5D-s. Tehát a 4D-s feltudatban a 3D-s világról gyűjtött kvázi 2D-s észleletek pont azáltal képesek összeállni 3D-s képpé, hogy 4D-s túltérbeli hullámképek (mozgó gravitációs hologramok, azaz gravíziók) formájában őrződnek meg és kerülnek feldolgozásra. Pontosan ezért nem képesek rájönni sem a materialista agykutatók, sem a lélek létezését tagadó (lélektelen) pszichológusok az emberi tudat működésének titkaira, mert ehhez nem elég a síkagyú, felszínes gondolkodás. Elméllyültségre és tartalmas (kitartó) megközelítésre van szükség a lényeg megértéséhez.
Ha egy meditáló szerzetes vagy misztikus képessé válik arra, hogy a lelke által érzékelt gravitációs hullámok képét tudatosan észlelje (tudomást vegyen róla), akkor elkezd belelátni a tárgyak belsejébe. Ezt hívják tévesen röntgen látásnak vagy radarszemnek, bár nyilvánvaló, hogy a dolognak semmi köze a röntgen sugárzáshoz, a radarberendezések működési elvéhez vagy pláne a fizikai szemhez. Lélekkel akkor is tisztán lehet "látni", ha csukva van az ember szeme vagy egyenesen testen kívül van az asztráltérben. Nem csupán 3D-ben, hanem 4D-ben is.
A fizikai szemmel való látás optikai élességének számos tényező szab határt a gyakorlatban. Ilyen a távolság, amivel négyzetes arányban gyengül (csak 3D-ben!) a céltárgyról érkező fény mennyisége. A közeg sűrűsége, ami szétszórja és elnyeli a fényt. A közeg törésmutatója, ami eltéríti a fényt és becsapja a látványt feldolgozó agyat a szokatlan perspektívával. A szemlencse görbülete és optikai hibái, melyek rontják a fény fókuszálását a látó területre. A látóidegsejtek száma, sűrűsége, érzékenysége és reakcióideje, amivel képesek a beérkező fényt (csak a látható tartományban) idegi impulzusokká alakítani. Az idegrendszer sávszélessége, amivel a jeleket továbbítja az agyba előfeldolgozásra, majd besugározza a lélekbe, ahol tudatosul. Mindezek miatt a szemmel való látás éppen csak elfogadható minőségű (valljuk be: elég gyenge) képet ad a tudatunk számára a 3D-s közegben való tájékozódáshoz.
A lélekbarion forrásrendszerével való közvetlen észleléskor, amit félrevezető módon szintén látásnak szoktunk nevezni (jobb szó híján), az anyagok gravitációs hullámai realizálódnak bennünk. Ez tűéles, pontosabban atomi (sőt szubatomi!) felbontású érzékelést jelent, ami sokkal kontrasztosabb az optikai látásnál. Amikor lélekkel nézünk, sokkal messzebbre látunk, ráadásul minden irányba egyszerre 360 fokban (minden dimenziószinten). Sokkal tisztább a kép (a 4D-s gravízió), információban messze gazdagabb és nem mosódnak el a részletek, mint a szem látómezejének perifériáján.
A lélek forrásrendszerének céltudatos eltorzításával lehetőség van a felbontás javítására, irányérzékennyé tételére. Ekkor egy adott irányban sokkal élesebben, messzebbre és jobban lehet látni, mint a többi irányban. Több száz méterről még könnyedén tudunk újságot olvasni vagy megnézhetünk egyes molekulákat, atomokat a környezetben, ami fölöttébb megkönnyíti például az orvosi diagnosztikát. Feltéve, hogy tudjuk, mi micsoda (méreg molekula, vírus, baktérium, sejtszintű elváltozás, stb).
További érdekesség, hogy mivel a lélekben őrződő minden információ is ugyanilyen időhullámokból áll, amik folyamatosan kisugárzódnak a barionból a környezetbe, ezért tisztán láthatók a többi lelkek gondolatai és érzései is. Elsősorban csak a domináns időhullámok, tehát ami éppen átfut az illetőn, de a rájuk szuperponálódó háttérzaj rezgései szintén észlelhetők. Ezen háttérzaj teljesen egyedi, s ennek alapján képesek a lelkek a túlvilágon (testen kívül) egyértelműen azonosítani egymást. Odaát ugyanis nincsenek nevek, arcok, személyi igazolványok, csak pontszerű lélek részecskék, akik mind egyedi és könnyen felismerhető hullámteret bocsátanak ki magukból. Ahhoz, hogy valaki képes legyen ebből a lelki háttérzajból kiemelni például az illető életének valamely korábbi emlékét, az addig összegyűjtött tudásának bármely részét, már speciális (mágia) technikára van szükség - az időfizika és n dimenziós időmatematika magasszintű tudása mellett. De ezt etikai okokból nem akarom ismertetni a 3D-s emberiséggel.
Ugyanígy a lélekszentély forrásrendszere által látott 5D-s külvilágképről sem sokat tudunk elmondani, mert az annyira más és különös élmény, hogy gyakorlatilag képtelenség 3D-s magyar nyelvre (vagy bármilyen más földi nyelvre) pontosan tolmácsolni. Az 5D-s közegben még élesebb képet lát a lélek, akár száz kilométerről lehet újságot olvasni és rengeteg izgalmas dolog figyelhető meg, aminek megtapasztalását minden megvilágosodott léleknek ajánljuk.
Kiegészítés: Magasabb dimenziókban nem csak lélekkel, hanem testi szemmel is lehet látni, mivel a felsőbb világokban szintén léteznek élőlények, így humanoidok is. Sikerült erről némi információt szereznünk (közvetlenül és médiumi beszélgetések révén), ami igen érdekes következtetések levonására ad lehetőséget. Ezzel később még foglalkozunk majd több emanikai írásunkban.
A legfontosabb parajelenség, hogy minden dimenziószinten eltérő az optikai látómező és a látott valóság kiterjedése és ezek egymáshoz való viszonya a fénytörés változásai miatt. A 3D-s emberi test két szemével kb. 120-150 fokos szélességű az optikai látómező és ugyanekkora a vele befogott valóság képe (ami a széle felé életlenebbé válik). A 4D-s hipertest szemével a látómező csak 60-90 fokos, mintha csőlátása lenne az embernek, míg a látómező sokkal szélesebb. Egy 180-210-240 fokos világ látható ezen belül, arányosan összenyomva. Ráadásul minden sokkal színesebb, élesebb és jóval távolabbra lehet ellátni. Az 5D-s extratest szemével a látómező már csak 30-45 fokos, egy kis cső az ember orra előtt, amin belül a még színesebb és még élesebb látvány 300-330-360 fokos szögben terjed ki minden irányban. Ezzel már simán el lehet látni a horizonton túlra (száz kilométerre). Ennél följebb, a 6D-ben már nincs anyag, ezért fizikai testek sem léteznek. Ott már csak lélekszentéllyel lehet látni, de ez nem hogy elmondhatatlan, hanem egyenesen felfoghatatlan 3D-s elmével.
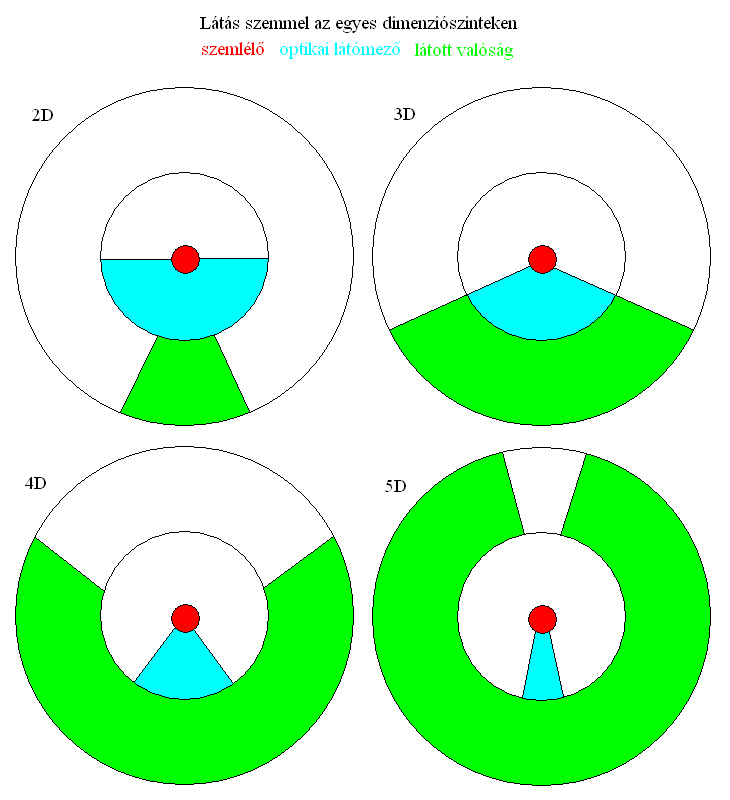
Bár lefelé még nem próbáltunk nézelődni, a felismert szabályok alapján valószínűsítjük, hogy az alsóbb dimenziószinteken, például a síkuniverzumban a látómező még tágabb (180 fok körüli), miközben egyre kevésbé élesen láthatunk jóval kisebb távolságra egy szűk tartományban (60-90 fokban). Ezzel együtt a színek száma is csökken, amivel részletesen egy külön írásban foglalkozunk a fénykvantumok működése kapcsán. A száluniverzumban már ugyancsak felfoghatatlanul sajátos képet kaphatunk a környezetről, míg a 0D-s pontállapotban (nirvána) gyakorlatilag nincs látnivaló.
6. EGY ELEKTRONIKUS VISSZACSATOLÁS
Ha egy videokamerát ráirányítunk egy televíziókészülékre, majd a felvett képet kiadjuk a tv ernyőjére, egy visszacsatolt rendszert kapunk, amin a körbeszaladó jel futási késedelme a kamera és a képernyő közti távolságtól, valamint a kábel hosszától és a megjelenítés sebességétől függ. A módszerrel főként a 90-es évek elején folytattak érdekes kísérleteket hazánkban és külföldön is a kutatók, mert nagyon érdekes, kaotikus és gyakorlatilag soha nem ismétlődő szép, sokszor fraktális mintázatok jelentek meg a monitoron, amit nem tudtak mivel magyarázni. Persze csak akkor, ha előbb az üres képernyőre rávilágítottak valamivel, megadva a kezdőlökést a gerjedésnek. Az volt a legfeltűnőbb a jelenségben, hogy a mintázat alapvetően háromféle viselkedést mutatott, ami attól függött, milyen messze volt a kamera a képernyőtől. Tehát a futási késedelem módosításával lehetett változtatni a képet.
Egy bizonyos távolságnál a kép gyakorlatilag egy helyben állva mozgott, forgott, örvénylett magában. Ha lecsökkentettük a távolságot, a kép folyamatosan futni kezdett középről kifelé, érdekes spirálokat, kiterjedő alakzatokat produkálva. Ha megnöveltük, a kép futni kezdett a szélétől befelé, a mintázatok összefutottak a közepén egy pontba. Erre sokáig nem találtunk magyarázatot, de ma már világos, hogy mi okozza ezt.
Az n dimenziós érzékelés alapjainak feltárása után egyértelmű, hogy amikor megfelelő távolságban van a kamera a képernyőtől, akkor azért áll a kép, mert épp a jelent látjuk. A kamera optikai lencséjének görbülete úgy fogja össze a beérkező fényt az érzékelő számára, hogy a (domború felszínű) képernyőtől távolodó gömbhullámok görbülete nagyjából egyszerre éri el a vevő síkfelületét. Ha kifut a kép középről, akkor a széleken a régebbi múlt pillanatai látszódnak, ha pedig befut, akkor középen látható a régebbi múlt. Ez hasonló az időfizikai modellekben szereplő kiáradó múlt és beáradó jövő hullámterének ábrázolásához.
7. AZ ISTENI RÁLÁTÁS
Az érzékszerveink által közvetített 2D-s információk a fejünkben 3D-s térbeli képpé, pontosabban mozgó filmmé állnak össze az agyi előfeldolgozás eredményeként. Ezután kerülnek be a lélekbe, ahol tudatosulnak, mint 4D-s élmények. A külső környezetünkben azonban számos olyan dolog van, ami sík rálátással nem értelmezhető kielégítően akkor sem, ha térbeli összképet alkotunk róla. Ez azzal jár, hogy a felületes észlelésből levont logikai tapasztalatok ellentmondásokhoz vezetnek az elmében. Főleg akkor, ha lehetőségünk van különböző helyekről (és eltérő időben) megfigyelni a jelenséget. Nagyon leegyszerűsítve arra hasonlít a helyzet, mint amikor két ember nézi ugyanazt a poharat és vitatkoznak a kinézetéről. Az egyik ember számára a pohárnak van füle, a másik számára nincs.
Egyes ellentmondások feloldhatók alaposabb 3D-s vizsgálattal és elemzéssel, mások nem. Ezekhez valószínűleg minimum 4D-s szemléletre volna szükség, mint amilyen a teleportáció, a gömbvillámok vagy a Klein-kancsó értelmezése. Az emberi tudat tehát vagy meghátrál a nehézség elől vagy kénytelen bevezetni az elvonatkoztatott gondolkodás segítségével a 4D-t, hogy fenntartsa a világ logikai konzisztenciáját. Az n dimenziós időmatematika rendszere is pontosan ezért készült.
Ha a teremtés egészében n-1D-s, akkor minden ennél alacsonyabb dimenziószámú látással szükségképpen ellentmondásosnak kell látszania. Csupán következtethetünk arra, hogy a dolgok mögött van magasabb szinten megnyilvánuló logikai összefüggés, de közvetlenül megtapasztalni nem tudjuk, az érzékszerveink korlátozott képességei miatt. Így viszont mindig akad fölfedeznivaló és van miről vitatkozni.
Tökéletes látása egyedül az egésznek, az Istennek van, ami azt jelenti, hogy neki minden pontjából egyszerre kell látnia önmagát ahhoz, hogy pontos és maradéktalan képe legyen róla. Ekkor viszont a mindent tudás állapotában van, ami nulla és végtelen információt jelent egyszerre az időtlenségben. Mert az idő is csak a szemlélőpont mozgása, áthelyeződése egyik fizikai pontból a másikba.
Ha viszont az Isten mindenhol ott van és mindent lát, akkor nincs más hely rajta kívül, ahová elmozdulhatna, hogy onnan is lásson valami újat. Az általa látott kép állókép, ami viszont értelmetlen, mert nincs mihez hasonlítani. Ezt a filozófiai ellentmondást az a fizikai tény oldja fel, miszerint az Isten (Teremtő okforrás) csak azon pontokból szemlélheti önmagát, ahol vannak másolati időforrásai az eseménytérben (nem a téridőben, hanem a minden létezőben). Ezek mellett természetesen rengeteg olyan további hely létezik még az egészben (például két időforrás között), ahol éppen nincs szemlélőpont. A sajátidő változása ugyan lehetővé teszi, hogy ott is legyen forráspont (a múltban vagy a jövőben), de egy adott pillanatban biztos nincs mindenhol, tehát a látvány nem lesz teljes. Így az időben előrehaladva végtelen mennyiségű olyan új, n-1D-s teljes látvány perturbálódhat az Isten szemlélőpontja számára állandóan, ami gazdagítja őt és egyben ellentmondásokat, problémákat kelt a számára.
Készült: 2004.06.27. - 2007.10.16.
Következő írás
Vissza a tartalomhoz