Ebben az írásunkban a dimenziók keletkezéséhez és működéséhez szeretnénk észrevételeket fűzni. Az időfizikai és időgeometriai modelljeink egyértelműen arra utalnak, hogy a térbeli kiterjedések működése az őket kiárasztó időhurkok ciklikusságán alapul. Ezt pedig többféle módszerrel lehet manipulálni, miáltal változatos terek kelthetőek. Csak ezen tereken belül képes a teremtés olyan bonyolult struktúrákat létrehozni, amilyenek az anyagi részecskék például. A sokféleség alapjai azonosak és egyszerűek, tehát alaposan meg kell vizsgálnunk őket, mindenféle megközelítésben, mielőtt az összetettebb rendszerek kutatásához fognánk. Az alábbiak megértéséhez ajánlott elolvasni a korábbi publikációkat időmatematikából.
1. A KÖR ÉS SZAKASZ MODELLJEI
Az 1D-s egyeneshez minimálisan 1D-s beágyazási környezetre van szükség. Az 1D-s körvonalhoz viszont 2D-s közeg kell. A kétféle szál között a különbség csupán annyi, hogy az egyik nyitott, másik zárt a két végén. Az egyenesnél két jelenpont növeszti az időszálat két irányba, míg a körön egy jelenpont generálja a szálat egyszerre két irányba. Mindkét rendszer keltéséhez azonban csak egy jelenpont szükséges, ezért kell a kört alapvetőbb (elsődlegesebb) kiterjedésnek tekintenünk az egyenesnél.
Az időbeli változás szempontjából az egyenes nyúlik, a körnek viszont növekszik a kerületi hossza, tehát tágul. A két kiterjedés között alapvető különbség van. Az egyenesnél a múltak helye nem változik (állnak) és a két jelen mozog, a körnél viszont a jelen áll és a múltak mozognak hozzá képest (méghozzá az összes t0-tól tn-ig). Ha a kör t0 pontja áll, akkor a jelennek is mozognia kell.
Ha keverjük a kettőt, a hibrid modellünkben két jelenpont fog mozogni egy körvonalon, egymással ellentétesen és körönként kétszer találkoznak, áthaladva egymáson. A kör nem változik, a múltak egymásra rakódnak. Lehet olyan modellt is csinálni, ahol egy jelen mozog egy egyenes mentén, de dupla múltat hagyva hátra, ez lesz az 1D-s szakaszkör (szállá lapított kör). További lehetőség, ha egy pont egyszerűen egy körvonal mentén mozog. Ez a ciklikus mozgás egy minimálkör esetén ekvivalens lesz a forgó, keringő ponttal. Abban az esetben, ha a pont egy szakaszkörön kering körbe, azt fogjuk látni, hogy a pont a szakasz két vége között jár oda-vissza, egyenetlen sebességgel (gyorsulva-lassulva). Ugyanez elképzelhető két jelenponttal is (a szakaszon két pont grasszál oda-vissza és középen találkoznak).
Ezek a leképzések egy időpont mozgását mutatják meg időben és térben különbözőképpen leképezve, 1D-ben és 2D-ben. A modell csak az idő telésének szálszerű ábrázolására alkalmas, de semmi többre. Nem lehet belőle tovább lépni fölfelé. A lehetőségek tehát a következők.:
Egy pontnál:
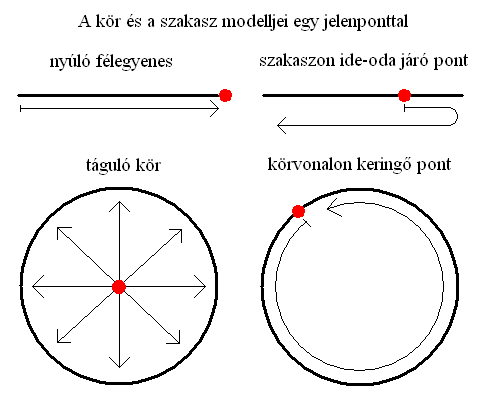
ha az 1D-s kiterjedés nyitott, akkor egy nyúló félegyenest kapunk.
ha az 1D-s kiterjedés zárt, akkor egy szakaszon ide-oda járó pontot kapunk.
ha a 2D-s kiterjedés nyitott, akkor egy táguló kört kapunk.
ha a 2D-s kiterjedés zárt, akkor egy körvonalon keringő pontot kapunk.
Két pontnál:
ha az 1D-s kiterjedés nyitott, akkor egy kétfelé nyúló egyenest kapunk.
ha az 1D-s kiterjedés zárt, akkor egy szakaszon ide-oda járó két pontot kapunk.
ha a 2D-s kiterjedés nyitott, akkor egy táguló kört kapunk.
ha a 2D-s kiterjedés zárt, akkor egy körvonalon keringő két pontot kapunk.
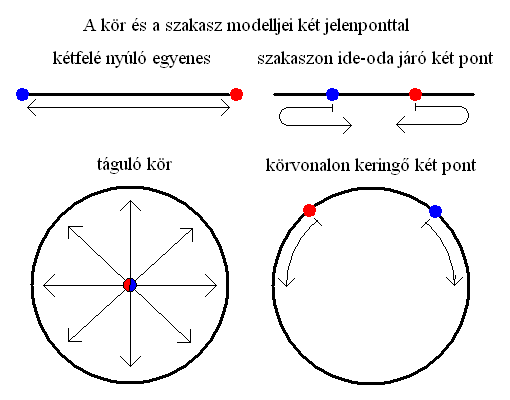
Amint látjuk, mindkét esetben csak egy olyan lehetőség van, amik azonosak egymással: a nyitott kiterjedések 2D-ben. A létezést forrását (jelenpontját) tehát akár egy pontnak tekintjük (Bindu), akár kettőnek (két Mandu), az időbeli és térbeli kiterjedése mindenképpen egy táguló kört fog alkotni.
2. TOVÁBBLÉPÉSI LEHETŐSÉGEK
Fel kell tennünk a kérdést, hogy miért növekszik meg a beágyazási környezet dimenziószáma, amikor egy ciklikus, önfenntartó rendszert (időhurkot) akarunk geometriailag jól leképezni? Akár térben, akár időben végezzük az ábrázolást, mindkét esetben magasabb kiterjedési számra van szükség a modellezéshez. Az ok logikailag összefüggésben áll Az attraktorok dimenziószáma című írásban foglaltakkal.
Ha a jelenpont egy szál mentén mozog ciklikusan, akkor időben kiterjesztve rendre átfedésbe kerül a saját múltjával egy cikluson belül, amikor a szakaszon oda-vissza halad. Ha a dimenziószám növelésével a rendszert térben kiterjesztjük, az ütközés elkerülhető, mert a pont egy 2D-s körön fog mozogni. Még ekkor is ütközni fog a korábbi múltjával egy kerületnyi út megtétele után, amin csak a sugár megváltoztatásával lehetne segíteni elvileg. Ekkor viszont a ciklus mérete hamar lecsökkenne nullára vagy megnőne a végtelenségig, ami sértené a visszacsatolás alapszabályát. A rendszer nem lenne képes időben haladva fenntartani önmagát, gyorsan szétesne és használhatatlanná válna a további műveletekhez.
Muszáj tehát a beágyazási környezetet kiterjeszteni a térbe, hogy a ciklus egy 3D-s gömbön belül fusson le. A 2D-s időspirál soha nem ismételheti önmagát, a 3D-s időgömb viszont igen. Mert a gömbnek nem csak a 2D-s felületén mozoghatunk, hanem mélységében is, belül maradva az attraktor vonzáskörzetén. Ahhoz tehát, hogy egy ciklikus rendszer jól modellezhető legyen, három környezeti változót, paramétert kell figyelembe vennünk: 1. a beágyazási környezet dimenziószáma. 2. a jelenpont mozgási dimenziója ebben. 3. a jelenpont által megtett útvonal, ami (a forrás pontszerűsége miatt) mindig 1D-s szál marad.
Mivel pedig a sajátidő állandóan előre halad a létezésben és sosem ismétli magát egy nyílt rendszerben (az időhurok ebből a szempontból csak kvázi zárt rendszer!), ezért az okforrások az őskáoszban nem fejlődhetnek tovább az 1D-s szálszerű világoknál (ezek a primer időszálak). A dimenziófejlődés tehát csakis az időhurkokban (önmásoló virtuális pontrendszerekben) történhet a teremtésben.
Az időhurok zárt időszerkezetnek tűnik az eseményének ismétlődése miatt, de valójában nyitott rendszer, mert a beágyazási környezetéből (őskáosz) folyamatosan perturbáló hatások érik. Ezek miatt bővül az információ tartalma, ami a térben új mozgási jellemzőként (n dimenziós, háttérzajszerű finom szitálásként) képeződik le a számára. Ettől nő szükségszerűen a dimenziószáma, mert a hurok (attraktor) ismétli is magát, meg nem is.
A ciklikus rendszerek jeleneinek mozgási pályája tehát akkor lesz egy attraktor körüli görbe, ha minimum egy 3D-s gömbhéj belsejében ábrázolható. Ezt nevezzük az időfizikában behúzási tartománynak (ami a külső és belső héjazat közti mezőnek felel meg). A behúzási tartomány tulajdonságaival későbbi időfizikai írásainkban még sokat foglalkozunk majd.
Készült: 2003.03.28. - 2005.11.26.
Következő írás
Vissza a tartalomhoz