1. BEVEZETÉS
A forgásról már több publikáció jelent meg az Eseményhorizonton, de még nem foglalkoztunk az n dimenziós kiterjedésű véges objektumok elforgatásának különféle eseteivel. Ebben az írásunkban végre pótoljuk a hiányosságot, mert kulcsfontosságú jelenségről van szó, aminek ismerete számos kutatási területen nélkülözhetetlen. A tömörség érdekében feltételezzük, hogy az Olvasó jártas az időfizika és időmatematika alapjaiban és ismeri a korábban közlésre került cikkeket.
Hétköznapi értelemben a forgás egy tárgy helyzetváltoztató mozgása a beágyazási környezetében (térben és időben), ami ciklikusan ismétlődik egy fordulatonként. Ilyenkor a tárgy pontjai a tárgyon (valahol) átmenő 1D-s egyenes (forgástengely) körül mozognak körpályán úgy, hogy közben megtartják az egymáshoz viszonyított helyzetüket (a tárgy nem deformálódik). Egy fordulatnak minősül a mozgásnak azon időbeli szakasza, melynek két végpontjában a tárgy pontjai a térben azonos helyet foglalnak el egy külső szemlélőponthoz viszonyítva. Egy mozgó pont akkor jut azonos helyre a térben egy külső szemlélőpont számára, ha a távolsága és irányszöge megegyezik a beágyazási környezetben.
Az időgeometriában a forgás meghatározása ennél sokkal bonyolultabb dolog, mert a tengely, az objektum (tárgy) és a beágyazási környezet dimenziószámától függ, milyen irányban végeznek mozgást az objektum pontjai. Ettől függetlenül azonban érvényesek maradnak azok a szabályok, miszerint a forgás az objektum helyzetváltoztató mozgása, ami ciklikusan ismétlődik egy fordulatonként. Az objektumot alkotó pontok pedig minden esetben körpályán mozognak úgy, hogy közben megtartják az egymáshoz viszonyított helyzetüket. Ez persze azt is jelenti, hogy az objektum kiterjedési számától függően forogni nem csak egy tengely körül lehet, hanem egy pont körül is. Sőt, megfelelő dimenziószám esetén sík, tér, túltér és bármilyen magasabb kiterjedés körül is elforgathatók a dolgok.
A forgásnak az aszimmetria tételből és a három pont tételből következően mindig két iránya lehet, melyek a fent és lent meghatározása esetén különböztethetők meg egymástól. Épp ezért a forgástengelyt a továbbiakban irányított szakasznak, vektornyílnak kell tekintenünk, amely mindig felfelé mutat. Az objektumok forgásirányát pedig mindig fentről (az északi pólus irányából) nézve kell meghatározni. A forgáspont, forgássík és forgástér esetében nem egyszerű feladat a vektornyíl irányának meghatározása, ezért ezzel a témával külön fejezetben foglalkozunk.
Ha a forgástengely áthalad az objektumon, az elmozdulását forgásnak nevezzük. Ha rajta kívül található, akkor keringésről beszélünk. A forgás és egyenes vonalú mozgás együttes folyamata a csavarvonalú mozgás, ami szintén két irányú lehet: balos és jobbos. Ha az egyenes vonalú mozgás iránya egybeesik a forgástengellyel, akkor spirálmozgásról beszélünk, ha pedig merőleges rá (a forgás síkja felé történik), akkor hurokmozgásnak hívjuk. Itt meg kell különböztetnünk egymástól a csavarvonalú mozgást a csavarodástól, mert a csavarvonalú mozgás nem deformálja a tárgyat, a csavarodás viszont igen.
2. N DIMENZIÓS FORGÁSOK
Forgassunk el különböző dimenziószámú objektumokat egy forgástengely körül. Az objektumok méretével most ne foglalkozzunk, tehát a művelet egyaránt vonatkozhat véges tárgyakra és végtelen kiterjedésekre. Mivel a tengely maga 1D-s, ezért gondok adódhatnak az elhelyezésével alacsonyabb dimenziókban. A 0D-s pontból például "kilóg" a tengely, az 1D-s egyenest pedig teljes egészében lefedi. A 2D-s síkba fektetett tengellyel az a gond, hogy két részre osztja (de nem határolja) a síkot. Ezért az azt alkotó pontok nem képesek ciklikus mozgást végezni a tengely körül anélkül, hogy megváltozna a tőle való távolságuk (körvonalon mozgás feltétele). A forgatás ez esetben tehát csak egy szinttel feljebb, 3D-ben értelmezhető. A 3D-s térben azonban már bárhogyan elhelyezhető a tengely, a forgatásnak nem lesz akadálya.
Ennek megfelelően különbséget kell tennünk azon esetek között, amikor a forgástengely a forgatandó objektum kiterjedésén belül található és amikor kilóg belőle. Az időmatematika lehetővé teszi, hogy az n dimenziós objektumok mindig elforgathatók legyenek egy n+1D-be kilógó tengely körül, mivel a beágyazási környezet dimenziószámának nincs felső korlátja.
Ha a forgástengely az n dimenziós objektum kiterjedési irányain belül található, akkor az egy fordulathoz szükséges beágyazási környezet térdimenziószáma a következőképpen alakul.:
0D-s objektum esetében: 1D-s beágyazási környezet szükséges.
1D-s objektum esetében: nincs változás (marad 1D).
2D-s objektum esetében: 3D-s beágyazási környezet szükséges.
3D-s objektum esetében: nincs változás (marad 3D).
4D-s objektum esetében: 5D-s beágyazási környezet szükséges.
5D-s objektum esetében: nincs változás (marad 5D).
6D-s objektum esetében: 7D-s beágyazási környezet szükséges.

Ha a forgástengely az n dimenziós objektum kiterjedési irányain kívülre esik, vagyis merőlegesen rájuk, akkor csak egy pontban metszi az objektum terét (forgáspontként viselkedik). Ebben az esetben az egy fordulathoz szükséges beágyazási környezet térdimenziószáma a következő lesz.:
0D-s objektum esetében: nincs változás (marad 0D).
1D-s objektum esetében: 2D-s beágyazási környezet szükséges.
2D-s objektum esetében: nincs változás (marad 2D).
3D-s objektum esetében: 4D-s beágyazási környezet szükséges.
4D-s objektum esetében: nincs változás (marad 4D).
5D-s objektum esetében: 6D-s beágyazási környezet szükséges.
6D-s objektum esetében: nincs változás (marad 6D).

Amint azt láthatjuk, a két lehetőség egymás komplementere. Ebből következik, hogy egy megfelelően elhelyezett forgástengely segítségével minden n dimenziós objektum körbeforgatható nD-ben és n+1D-ben egyaránt. Felmerül a kérdés, hogy vajon n+2, n+3 és magasabb dimenziókban is elforgathatók-e az objektumok? Az nyilvánvaló, hogy n-1D-ben nem értelmezhető a forgás jelensége, mert a kiterjedés redukciója deformálná az objektum szerkezetét. Mielőtt azonban megválaszolnánk a kérdést, meg kell határoznunk azokat a leképzési lehetőségeket, melyek keretein belül az alapvető mozgások (és így a forgás is) értelmezhetővé válnak.
3. LEKÉPZÉSI LEHETŐSÉGEK
Tapasztalati ténynek tekintjük, hogy a forgás az időben helyváltoztató mozgásnak, a térben viszont helyzetváltoztató mozgásnak minősül. A forgó tárgy tehát a sajátidejében előre halad, míg a sajátterében körbe mozog (ciklikusan). A természetben azonban léteznek másféle mozgáskombinációk is, mivel összesen négyféleképpen lehet leképezni a különböző (alapvető) mozgásokat a téridőben.
1. Időben helyváltoztató és térben is helyváltoztató.
2. Időben helyváltoztató, térben helyzetváltoztató.
3. Időben helyzetváltoztató és térben is helyzetváltozató.
4. Időben helyzetváltoztató, térben helyváltoztató.
Az egyenes vonalú mozgás időben és térben is helyváltoztató (1). A forgás időben helyváltoztató, térben helyzetváltoztató mozgás (2). A kvázi egy helyben álló időhurok (szerinó) időben és térben is helyzetváltoztató mozgást végez (3). A száguldozó időhurok (fotinó) pedig időben helyzetváltoztató, térben helyváltoztató rendszerként viselkedik (4).
A makro világ jelenségei (tárgyak) az időben látszólag helyváltoztató mozgást végeznek, mert folyamatosan haladnak előre a múlt irányából a jelenen át a jövő felé. A mikro világ jelenségei, a ciklikusan körbemásolódó és ezért önfenntartó időforrás látomások viszont pont fordított viselkedést mutatnak. Egy végesen kicsiny időszakaszon belül mozognak körbe-körbe, folyton ismételve a korábbi pillanatokat.
Ebből a tényből következik, hogy ha a tárgyak megfelelő térbeli elforgatások révén tükrözhetők (tértükrözéssel), akkor az időhurkok megfelelő időbeli elforgatások révén tükrözhetők (időtükrözéssel). Az időtükrözés (valamint az időtükrök és az időutazás) jelenségével azonban a téma bonyolultsága miatt egyelőre nem foglalkozunk. Majd egy későbbi időpontban kerítünk sort az időmatematikai elemzésükre. Mivel azonban a forgásnak szoros kapcsolata van a tükrözéssel, vizsgáljuk meg ennek lehetőségeit n dimenzióban.
4. AZ ELFORGATÁS TÜKRÖZŐ HATÁSA
Ha 180 fokkal elforgatunk egy 2D-s síklapot a saját kiterjedésében, nem változnak meg tulajdonságai, vagyis önmaga marad. Ha viszont 3D-ben forgatjuk el, akkor önmaga tükörképévé válik. Vajon ha a síklapot 4D-ben forgatjuk körbe, akkor is tükörkép lesz belőle vagy nem?
Ennek megértéséhez előbb vizsgáljuk meg, mi történik az alacsonyabb kiterjedési számú objektumokkal hasonló esetben. Az 1D-s szakasz 180 fokkal való elforgatása a saját kiterjedésében nem változtatja meg a szakaszt. Ha viszont 2D-ben forgatjuk el, akkor önmaga tükörképévé válik. Ugyanez történik akkor is, ha a síkra merőlegesen, 3D-ben forgatjuk el a szakaszt, mivel ezzel csupán a forgási síkját mozgattuk el egy dimenzióval följebb, ami a szakasz számára nem jelent semmiféle változást önmagához képest.
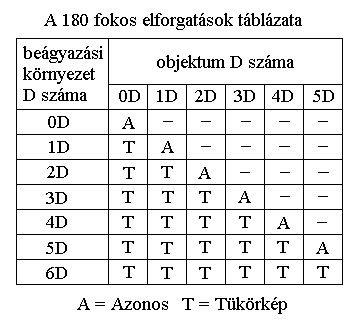
Ebből levonhatjuk a nyilvánvaló következtetést, hogy egy n dimenziós objektum 180 fokos elforgatása minden nagyobb kiterjedési számú beágyazási környezetben (n+1, n+2, n+3, stb.) tükrözi azt. Ez egyben azt is jelenti, hogy a forgás csak n és n+1 dimenzióban értelmezhető mozgásjelenség, feltéve, hogy a tengely maximum n-1 dimenziós. A következő fejezetben éppen ezért megvizsgáljuk az n dimenziós forgástengelyek tulajdonságait.
5. N DIMENZIÓS TENGELYEK
Kezdjük a legegyszerűbb lehetőséggel, a forgástengellyel és a belőle képezhető forgásponttal. Az 1D-s egyenes körbeforgatható egy rá merőleges forgástengely körül a 2D-s síkban. Ehhez a művelethez azonban 3D-s beágyazási környezet szükséges, mert a forgástengelynek merőlegesnek kell lennie a síkra. Ha jobban megvizsgáljuk a folyamatot, azt fogjuk találni, hogy az egyenes elforgatásához nincs szükségünk egy egész (1D-s) forgástengelyre. Bőven elég a tengelynek az a része, mely metszi az egyenest. Mivel az 1D-s egyenes a három pont tételből következően csak egy vagy két pontnyi széles lehet, ezért a metszet egy vagy két pontja nem alkot minimálszakaszt. Ez a tény teszi geometriailag lehetővé, hogy a forgatást egy pont körül végezzük. Mindezzel nem szegtük meg a forgás definícióját, miszerint egy szálszerű tengely körül kell mozognunk, csupán egyszerűsítettük a feladatot.
A 3D-s tér körbeforgatható egy rá merőleges forgástengely körül a 4D-s túltérben. A tengely a három pont tételből következően csak egy vagy két pontnyi hosszúságban metszi a 3D-s teret, vagyis nem alkot minimálszakaszt. Ez a tény teszi geometriailag lehetővé, hogy a forgatást egy pont körül végezzük. Fizikailag ez olyan látvány a 3D-ből szemlélve, mintha a forgó tárgy azonnal eltűnne a szemünk elől, és csupán egy kis pont maradna belőle ott, ahol a forgástengely metszi a teret. 180 foknyi elfordulás után hirtelen megjelenne a tárgy, de tükröződve (antianyagként), ami rögtön igen látványos annihilációs robbanást okozna, elvéve kedvünket a további szemlélődéstől. Tovább forgatva a tárgy (feltéve, hogy megmarad belőle valami) ismét eltűnik, majd újabb 180 foknyi elfordulást követően az eredeti alakjában megjelenik a térben. A 3D-ben végzett pont körüli forgatás tehát egyenlő a 4D-ben végzett tengely körüli forgatással.
Ennek a szabálynak megfelelően logikusnak tűnik, hogy ha a 4D-ben lévő forgástengely a 3D-ben forgáspontnak látszik, akkor a 4D-ben lévő forgássík a 3D-ben forgástengelynek látszik, mivel merőleges annak kiterjedésére és csak egy egyenes mentén metszi a 3D-t. Ekörül elforgatva a 3D-t tehát nem történik tükröződés. Fölfelé kiterjesztve a modellt azt mondhatjuk, hogy a 4D-ben lévő forgássík az 5D-ben kiterjeszthető forgástérré, a 6D-ben forgástúltérré, stb.
Ugyanezt megfogalmazhatjuk úgy is, hogy az 1D-s egyenes elforgatható a 0D-s forgáspont körül a 2D-ben, a 2D-s sík elforgatható az 1D-s forgástengely körül a 3D-ben, a 3D-s tér elforgatható a 2D-s forgássík körül a 4D-ben, a 4D-s túltér elforgatható a 3D-s forgástér körül az 5D-ben, az 5D-s kültér elforgatható a 4D-s forgástúltér körül a 6D-ben, stb.
A következő kérdés, amit meg kell vizsgálnunk, hogy vajon a forgáspont, forgássík és forgástér, mint kvázi vektornyíl merrefelé mutat? Enélkül nem tudjuk ugyanis meghatározni a forgás irányát, mert nem értelmezhető a fent és a lent a tengely mentén. A fenti szabály azonban egyszerű megoldást kínál a problémára, mert minden n dimenziós tengely konvertálható 1D-s forgástengellyé. Tehát meg kell nézni, hogy az 1D-s szál körbeforgatva a 0D-s forgáspont körül hogyan mozog a 3D-ből szemlélve? A forgásponton keresztül állítani kell egy egyenest a 3D-ben, merőlegesen a forgás körvonalának síkjára, amin már kijelölhető a vektornyíl iránya. A 3D-ben lévő 2D-s forgássík egy rá merőleges síkot 1D-s egyenes mentén metsz, ahogy a 4D-ben lévő 2D-s forgássík a 3D-t egy 1D-s egyenes mentén metszi. Itt csak azzal a problémával kell megküzdenünk, hogy a forgássíkot milyen szögben kell metszenünk az alsóbb szintű beágyazási környezetben? Mert ugye a 3D-ben egy forgássíkra két merőleges síkot lehet állítani, melyek egymásra is merőlegesek (lásd a Merőlegesség n dimenzióban című írást). A forgásirány ettől persze nem fog megváltozni, vagyis bármelyiket választjuk, ugyanazon eredményre jutunk.
6. N DIMENZIÓS KERINGÉSEK
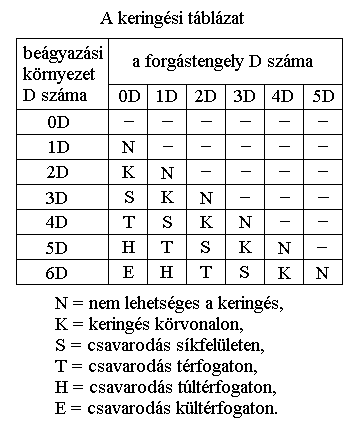
A keringést olyan mozgásnak tekintjük, ahol az objektum teljes egészében megkerüli a forgástengelyt (vagy forgáspontot, forgássíkot, forgásteret, stb.) anélkül, hogy metszené azt (áthatolna rajta). Erre azonban nem minden esetben van lehetőség, mert alapvetően a beágyazási környezet dimenziószámától függ, hogy a tengely megkerülhető-e? Az alábbiakban felsoroljuk a különféle lehetőségeket.:
Az 1D-s szálat a 0D-s forgáspont két részre osztja (de nem határolja topológiailag), ezért a pontok és szakaszok nem tudnak 1D-ben keringeni körülötte. A 2D-s síkban viszont lehet keringeni a 0D-s forgáspont körül.
A 2D-s síkot az 1D-s forgástengely két részre osztja (de nem határolja topológiailag), ezért a pontok, szakaszok és síkidomok nem tudnak 2D-ben keringeni körülötte. A 3D-s térben viszont lehet keringeni az 1D-s forgástengely körül.
A 3D-s teret a 2D-s forgássík két részre osztja (de nem határolja topológiailag), ezért a pontok, szakaszok, síkidomok és térbeli testek nem tudnak 3D-ben keringeni körülötte. A 4D-s túltérben viszont lehet keringeni a 2D-s forgássík körül.
A 4D-s túlteret a 3D-s forgástér két részre osztja (de nem határolja topológiailag), ezért a beleágyazott objektumok nem tudnak 4D-ben keringeni körülötte. Az 5D-s kültérben viszont lehet keringeni a 3D-s forgástér körül.
Az 5D-s külteret a 4D-s forgástúltér két részre osztja (de nem határolja topológiailag), ezért a beleágyazott objektumok nem tudnak 5D-ben keringeni körülötte. A 6D-s feltérben viszont lehet keringeni a 4D-s forgástúltér körül.
Most fogalmazzuk meg másként a fentieket, hogy egyértelműbb legyen a szabály.:
Az 1D-s szakasz a 0D-s forgáspont körül a 2D-s beágyazási környezetben elforgatható.
A 2D-s síklap az 1D-s forgástengely körül a 3D-s beágyazási környezetben elforgatható.
A 3D-s térbeli test a 2D-s forgássík körül a 4D-s beágyazási környezetben elforgatható.
A 4D-s túltérbeli test a 3D-s forgástér körül az 5D-s beágyazási környezetben elforgatható.
Az 5D-s kültérbeli test a 4D-s forgástúltér körül a 6D-s beágyazási környezetben elforgatható.
A 6D-s feltérbeli test az 5D-s forgáskültér körül a 7D-s beágyazási környezetben elforgatható.
Képlettel felírva az n dimenziós keringési szabályt: B=F+2, ahol B a beágyazási környezet dimenziószáma, F a forgástengely dimenziószáma. Mindez természetesen nem jelenti azt, hogy pl. a forgáspont körül 2D-ben nem keringhet egy 2D-s síkidom vagy a forgástengely körül 3D-ben nem keringhet egy 3D-s térbeli test, stb. Viszont egy forgáspont körül a 3D-ben nem körpályán, hanem egy gömb felülete mentén mozoghatnak a tárgyak, tetszőlegesen bonyolult elcsavarodó pályagörbéket írva le. A 4D-ben egy forgáspont körül egy hipergömb térfogata mentén mozoghatnak a tárgyak, míg egy forgástengely körül ismét egy gömb felülete mentén mozoghatnak. Az alábbi táblázat az n dimenziós tengelyek körbejárhatóságát mutatja.
A keringési szabály ilyen speciális módon való megfogalmazására pont azért volt szükség, hogy lássuk: az n dimenziós objektumok n+1 dimenzióban olyan pályákon keringhetnek, melyeken félfordulatonként önmaguk tükörképévé válnak. Itt kapcsolódik a téma az n dimenziós tükrözési szabályokhoz, mert egy fizikailag könnyen megvalósítható lehetőségét adja számunkra a dolgok tükrözésének.
A tárgyak tükröződése persze a gyakorlatban rengeteg veszéllyel és problémával jár, gondoljunk itt elsősorban az anyag antianyaggá alakulásának következményeire. Éppen ezért a következő fejezetben felsoroljuk mindazokat az n dimenziós elforgatásokat, amik a fellépő veszélyek miatt tiltottnak minősülnek a számunkra.
7. TILTOTT ELFORGATÁSOK
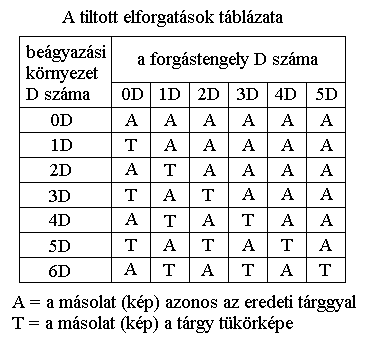
Tiltott elforgatási műveletek a gyakorlatban:
1. A 2D-s síkot a benne lévő 1D-s forgástengely körül tilos 180 fokkal elforgatni a 3D-ben. Ez egyenértékű a tengelyes tükrözéssel.
2. A 3D-s teret a belőle kilógó 1D-s forgástengely körül tilos 180 fokkal elforgatni a 4D-ben. Ez egyenértékű a középpontos tükrözéssel.
3. A 4D-s túlteret a benne lévő 1D-s forgástengely körül tilos 180 fokkal elforgatni az 5D-ben. Ez egyenértékű a tengelyes tükrözéssel.
4. Az 5D-s külteret a belőle kilógó 1D-s forgástengely körül tilos 180 fokkal elforgatni a 6D-ben. Ez egyenértékű a középpontos tükrözéssel.
5. A 6D-s felteret a benne lévő 1D-s forgástengely körül tilos 180 fokkal elforgatni a 7D-ben. Ez egyenértékű a tengelyes tükrözéssel.
Ez a sorozat tetszőlegesen folytatható fölfelé n dimenzióban. További veszélyforrások lehetnek még a gyakorlatban a következő bonyolultabb műveletek.:
1. A 3D-s teret a benne lévő 2D-s forgássík körül tilos 180 fokkal elforgatni a 4D-ben. Ez egyenértékű a síktükrözéssel.
2. A 4D-s túlteret a belőle kilógó 3D-s forgástér körül tilos 180 fokkal elforgatni az 5D-ben. Ez egyenértékű a tértükrözéssel. A 3D-s forgástér egyébként a 4D-s túlteret valószínűleg egy 2D-s síklapként metszi, tehát mintha ezen sík körül forgatnánk el a túlteret.
3. Az 5D-s külteret a benne lévő 2D-s forgássík körül tilos 180 fokkal elforgatni a 6D-ben. Ez egyenértékű a síktükrözéssel.
4. A 6D-s felteret a belőle kilógó 3D-s forgástér körül tilos 180 fokkal elforgatni a 7D-ben. Ez egyenértékű a tértükrözéssel. A 3D-s forgástér egyébként a 6D-s felteret valószínűleg egy 2D-s síklapként metszi, tehát mintha ezen sík körül forgatnánk el a felteret.
5. Az 5D-s külteret a benne lévő 4D-s forgástúltér körül tilos 180 fokkal elforgatni a 6D-ben. Ez egyenértékű a túltértükrözéssel.
6. A 6D-s felteret a belőle kilógó 5D-s forgáskültér körül tilos 180 fokkal elforgatni a 7D-ben. Ez egyenértékű a kültértükrözéssel.
Ez a sorozat is tetszőlegesen folytatható fölfelé n dimenzióban.
8. TECHNOLÓGIAI KÖVETKEZMÉNYEK
A térugró hajtóművel felszerelt űrhajóink képesek lesznek mozogni a 4D-s túltérben, ezért a személyzetükre állandó veszélyt jelent majd a tükröződve visszalépés a 3D-s téridőbe. Az annihilációs robbanás elkerülése érdekében a járműveknek szükségük lesz egy olyan navigációs berendezésre, amely képes meghatározni az űrhajó térbeli helyzetét a 4D-ben és összehasonlítani azt a 3D-s kiterjedés állapotával. Még a beugrás előtt, hogy megfelelő szögben érkezzen a hajó az alsóbb dimenzióba. A témával bővebben a térugrás technológia kutatási anyagaiban foglalkozunk, térforgásirány szinkronizátor címszó alatt.
A forgássík körül történő elmozdulás lehetővé teszi majd, hogy a több ablakos térkapuk felületeit egy térlapozásnak nevezett módszerrel cserélgessük a 4D-n keresztül a kapu keretében. Ezzel bővebben a térablak technológia elméleti alapjait ismertető publikációkban foglalkozunk majd.
A 3D-s térbúrát a rendszert fenntartó Napistennek egy forgássík körül kell elforgatnia a 4D-ben ahhoz, hogy konzisztensen mozogjon (keringjen) és égindulás legyen a művelet eredménye. Az égindulás következményeit részletesen lásd a Kozmikus katasztrófák című írásban a 2006-os év anyagai között.
Készült: 2004.03.15. - 2005.10.10.
Következő írás
Vissza a tartalomhoz