1. AZ OKTAÉDER SOROZAT
Az időmatematikában az egymásra merőleges egyeneseket (szakaszokat) a számuktól függetlenül térkeresztnek hívjuk. A segítségükkel állíthatók elő az oktaéder sorozat objektumai, amennyiben a szakaszok végpontjait egyenesekkel összekötjük. Az alábbi táblázatban ezen geometriai sorozatot tüntettük föl. A térkeresztről további információk olvashatók A három pont tétel és A tér matematikai szerkezete című írásokban.
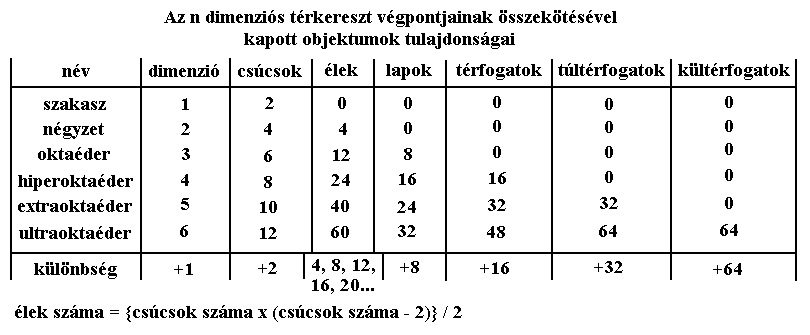
A csúcsokat összekötő élek számának meghatározásához azt kell tudni, hogy az n dimenziós térkereszten bármely csúcsból nézve mindig csak egy olyan csúcs van, aminek a távolsága nagyobb a többinél. Ez a térkereszt szálának (a testátlónak) a túlsó vége. Ha az élhosszúság egy, akkor a testátló túlvégén lévő pont távolsága gyök kettő. Tehát minden csúcs n-2 másik csúccsal van közvetlenül él mentén összekötve, ami n csúcs esetén (nx(n-2))/2 élt fog jelenteni.
Érdekes anomália lesz az oktaéder sorozat esetén az, hogy az n dimenziós objektumoknak nincs n dimenziós alkotója. Tehát a szakasznak 0 éle van, a négyzetnek 0 lapja, az oktaédernek 0 térfogata, stb. Ennek két oka van. Egyrészt mert a táblázatban így lesznek korrektek a matematikai sorozatok függőlegesen. Összehasonlításképpen nézze meg az Olvasó a kocka sorozat táblázatát a következő fejezetben, ahol minden oszlopban a sorozatok eggyel kezdődnek. Még a csúcsoknál is, mert a 0D-s kockának (pontnyi) szükségképpen 1 csúcsa kell, hogy legyen a szabály szerint.
Másrészt, mert a három pont tételből tudjuk, hogy az oktaéder csúcspontjai önmagukban nem felelnek meg a minimális kiterjedésekre vonatkozó szabályoknak. A létező legkisebb szakasz három pont hosszúságú, míg az 1D-s oktaéder (szakasz) képzéséhez csak két pontra van szükség. A legkisebb sík öt pontból áll, míg a 2D-s oktaéder (négyzet) képzéséhez csak négy pontra van szükség. A legkisebb tér hét pontból áll, míg a 3D-s oktaéder képzéséhez csak hat pontra van szükség, stb. A minimáloktaéder tehát kevesebb pontból áll, mint a minimáltér, ezért nem tekinthető valódi 3D-s objektumnak. De 2D-snek és 1D-snek sem, mivel minden irányban (a ráillesztett térkereszt alapján) kisebbnek mutatkozik a minimális kiterjedésnél.
Ezt az anomáliát az teszi lehetővé, hogy az n dimenziós oktaédert elforgatások segítségével állítjuk elő az n-1 dimenziós oktaéderből és végső soron a létező pontból (ami két pontot jelent). A forgáshoz pedig nincs szükség valódi térbeli (dimenzionális) kiterjedésre, ellentétben a kockával, ahol szálirányú eltolásokkal képezzük a magasabb dimenziószintű objektumokat. A minimálszál (minimálszakasz) pedig már három pont hosszú, tehát az n dimenziós minimálkocka mindig több pontból áll, mint az n dimenziós minimálkiterjedés.
Időfizikai kiegészítés: A térszerán működése során az időhurokban száguldó forráspontok (látomások) egy torz oktaéder csúcspontjain villannak fel kívülről nézve. Az oktaéder valójában csak piramis, mert a hatodik csúcsán mindig éppen hiányzik az utolsó forrás. Ez a keltési ciklus végén jelenik meg egy eszményien rövid pillanatra, amikor a formáját változtató oktaéder éppen eléri a szabályos geometriai szerkezetet és a ciklus visszaugrik az első pillanatra, elölről kezdve a rendszer keltését. Menet közben a térszerán origójában (pontosabban annak környékén egy szűk tartományon belül) rendre megjelenik a tachion felvillanások eredményeként egy álló, női típusú okforrás fiatalkori képe. Ő a királylány, aki nélkül a rendszer nem maradhatna életben, s ezért biztosítja a téridő kiáradását, felfúvódását. Így az origó ponttal rendelkező oktaéder már kielégíti a minimáltérre vonatkozó szabályt (a hét pontjával), vagyis lesz valódi térfogata. Ezért van a téridőnek térfogata (3D-ben), míg a túltérnek túltérfogata (4D-ben).
2. A KOCKA SOROZAT
A kocka sorozat objektumai, melyek az oktaéder sorozat azonos dimenziószámú objektumainak duálisai, egy szakaszon végzet párhuzamos eltolások segítségével állíthatók elő. Az alábbi táblázatban ezen geometriai sorozatot tüntettük föl.
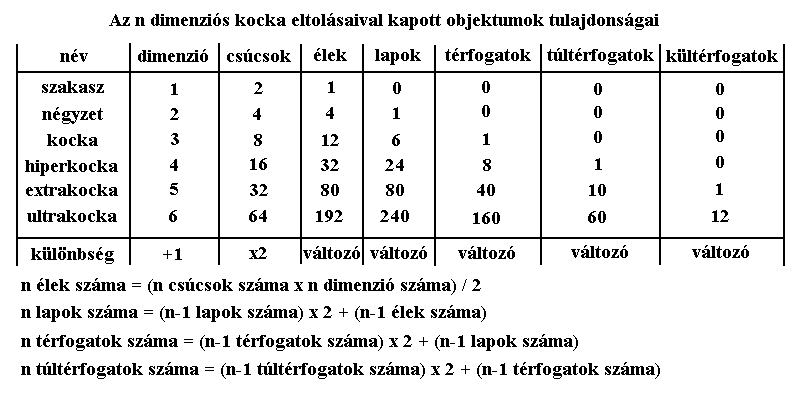
A kocka csúcsainak száma minden eltolás során duplázódik, mert a meglévő n-1 dimenziós objektumot húzzuk el n dimenzióban, gyakorlatilag nyújtást végezve rajta. A csúcsokat összekötő élek számának meghatározásához pedig azt kell tudni, hogy az élek mindig merőlegesek egymásra, tehát úgy viselkednek, mint egy térkereszt szárai. Ezért a csúcsok számát meg kell szorozni a kiterjedés dimenziószámával és ennek a felét kell venni, hogy ne számoljunk minden élt kétszer.
A lapok száma az eltolás során úgy nő, hogy az n-1 dimenziós objektum lapszáma megduplázódik, amihez hozzá kell adni annyi további lapot, ahány éle van az n-1 dimenziós objektumnak. Ezt a szabályt aztán az összes magasabb kiterjedési számú alkotóra is változatlanul lehet alkalmazni, lásd a táblázat alatti képleteket.
3. A MERŐLEGESSÉGI SOROZAT
A 2D-s síkban el lehet helyezni 2 db egymásra merőleges egyenest. A 3D-s térben el lehet helyezni 3 db egymásra merőleges egyenest vagy 3 db egymásra merőleges síkot. Vagyis a 3D-ben minden síkon 2 db egyenes van és minden egyenesen 2 db sík halad át. Elvileg ekkor a 3 egyenesen 6 síknak kellene áthaladnia, de mivel ezek páronként azonosak, a síkok száma csak 3 db. Ezen összefüggések alapján próbáljuk meghatározni, hogy magasabb dimenziószinteken hány darab egymásra merőleges alacsonyabb kiterjedést lehet elhelyezni?

A 4D-s túltérben el lehet helyezni 4 db egymásra merőleges egyenest vagy 4 db egymásra merőleges teret. Ha 2D-ben egy egyenest egy sík tud metszeni, a 3D-ben pedig kettő (melyek merőlegesek egymásra), akkor a 4D-ben három. Vagyis a 4D-ben minden síkon 2 db egyenes van és minden egyenesen 3 db sík halad át. Elvileg ekkor a 4 egyenesen 12 síknak kellene lennie, de mivel ezek páronként azonosak, a síkok száma csak 6 db.
A 4D-ben minden térben 3 db egyenes van és minden egyenesen 3 db tér halad át. Elvileg ekkor a 4 egyenesen 12 térnek kellene áthaladnia, de mivel ezek hármassával azonosak, a terek száma csak 4 db.
Az 5D-s kültérben el lehet helyezni 5 db egymásra merőleges egyenest vagy 5 db egymásra merőleges túlteret. Az 5D-ben egy egyenest négy sík tud metszeni, vagyis minden síkon 2 db egyenes van és minden egyenesen 4 db sík halad át. Elvileg ekkor az 5 egyenesen 20 síknak kellene lennie, de mivel ezek páronként azonosak, a síkok száma csak 10 db.
Az 5D-ben minden térben 3 db egyenes van és minden egyenesen 6 db tér halad át. Elvileg ekkor az 5 egyenesen 30 térnek kellene áthaladnia, de mivel ezek hármassával azonosak, a terek száma csak 10 db.
Az 5D-ben minden túltérben 4 db egyenes van és minden egyenesen 4 db túltér halad át. Elvileg ekkor az 5 egyenesen 20 db túltérnek kellene áthaladnia, de mivel ezek négyessével azonosak, a túlterek száma csak 5 db.
Az alábbi táblázatban ezen geometriai sorozatot tüntettük föl.
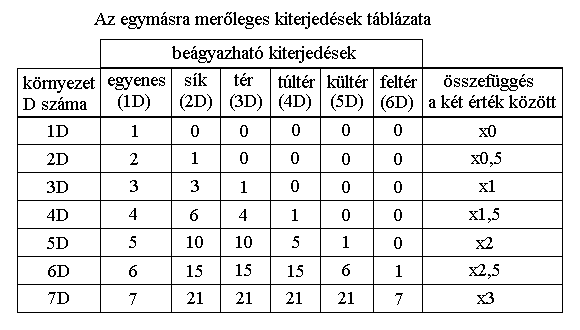
Időfizikai kiegészítés: A térszerán hullámterének szerkezete pontosan követi ezt a levezetést, mert ott 5 db 4D-s túltér alkotja együttesen a térhatosban az 1 db 5D-s külteret. Lásd: A tér fizikai szerkezete című írást.
Készült: 2007.04.30.
Frissítés:
n térdimenziók száma: 1-től 6-ig.
cs csúcsok száma: 2^n
é élek száma: (nxcs)/2
l lapfelszínek száma: ((n-1)xé)/4
t térfogatok száma: ((n-2)xl)/6
h túltérfogatok száma: ((n-3)xt)/8
e kültérfogatok száma: ((n-4)xh)/10
u feltérfogatok száma: ((n-5)xe)/12
A négyzet lapátlója: gyök 2 (=1,414).
A kocka testátlója: gyök 3 (=1,732).
A hiperkocka túltestátlója: gyök 4 (=2).
Az extrakocka kültestátlója: gyök 5 (=2,236).
Az ultrakocka feltestátlója: gyök 6 (=2,449).
Angol nyelvű videó az n dimenziós kocka alkotóinak levezetéséről:
Penrose Tilings from Five Dimensions:
https://www.youtube.com/watch?v=jJOTM2UGx70
Frissítve: 2024.07.18.
Következő írás
Vissza a tartalomhoz