1. BEVEZETÉS
Hétköznapi értelmében a tükrözés az a folyamat, amikor egy tükröző felületről visszaverődő fény segítségével meglátjuk önmagunk másolatát, tükörképét a felületen. A tükörkép a valóság egyfajta virtuális leképzése, ami nem azonos vele, mert benne az irányok megfordulnak. Geometriailag a klasszikus síktükör a síkjára merőleges irányt fordítja meg (180 fokkal) az előre-hátra tengelyen. A tükröződés csak a koordináta rendszer körüljárási irányát változtatja meg, felcserélve a balos és jobbos forgásirányokat. A matematikában a tükrözésnek több fajtája van. A leggyakrabban használt tükrözések a középpontos, tengelyes, sík és tértükrözések.
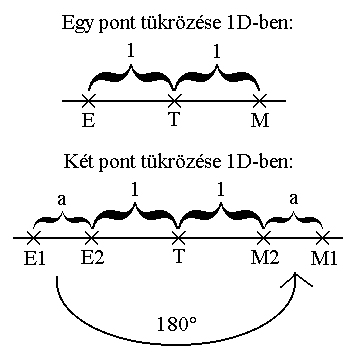
Ebben az írásunkban azt szeretnénk bemutatni, hogy az n dimenziós objektumok tükrözése a különböző dimenziószámú tükrök segítségével milyen tükörképeket hoz létre. A tükörképek ugyanis egyes esetekben azonosak az eredeti tárggyal, más esetekben viszont nem. Itt most nem foglalkozunk a tükör geometriai jellemzőivel (görbeség), sem fizikai tulajdonságaival (fényvisszaverő képesség), ezért minden esetben ideális tükrökről van szó, melyek segítségével az eredeti tárgynak elkészíthető a másolata.
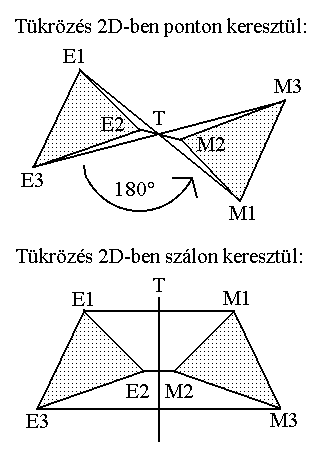
A tükrözési folyamat geometriai megközelítésben alapvetően azt jelenti, hogy a tárgy minden pontjából merőleges egyenest állítunk a tükörre, majd ezt meghosszabbítjuk a tükör túloldalán, ahova rámérjük a tárgypont - tükör távolságot. Az egyenesek egyes esetekben párhuzamosak lesznek egymással, máskor nem - bizonyos szabályok szerint. Kezdjük ezért a vizsgálódásainkat ezen tükrözési egyenesek tulajdonságainak feltérképezésével.
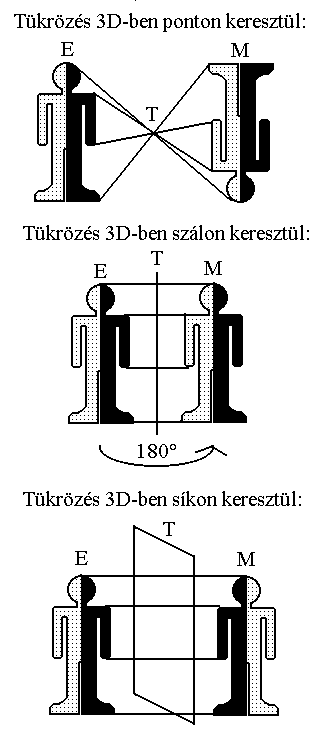
2. A TÜKRÖZÉSI EGYENESEK
Ha a tárgyakat valódi létező objektumoknak tekintjük, akkor minden pontjukból a létezésük eseményhorizontjai gömbszerűen fúvódnak fel. Ezen gömbök térdimenziószáma azonos a beágyazási környezet térdimenziószámával. Annak a gömbnek a sugara, amely egy pontban érinti a tükröt, azonos a pontból a tükörre állított merőleges szakasszal (a köztük lévő legkisebb távolsággal). Ezek az egyenesek egyes esetekben párhuzamosak egymással, máskor nem. Attól függően, hogy a tárgy dimenziószáma azonos a beágyazási környezetével vagy annál kisebb, eltérő lesz az egyenesek állásszöge.
Például egy 2D-s tárgyat a 2D-s beágyazási környezetben párhuzamos egyenesekkel lehet tükrözni egy 1D-s tükörre, míg 3D-s beágyazási környezetben nem. Ugyanígy egy 3D-s tárgyat a 3D-s beágyazási környezetben párhuzamos egyenesekkel lehet tükrözni egy 2D-s tükörre, míg 4D-s beágyazási környezetben nem. Az alábbi táblázatokban a különféle lehetőségek láthatók.
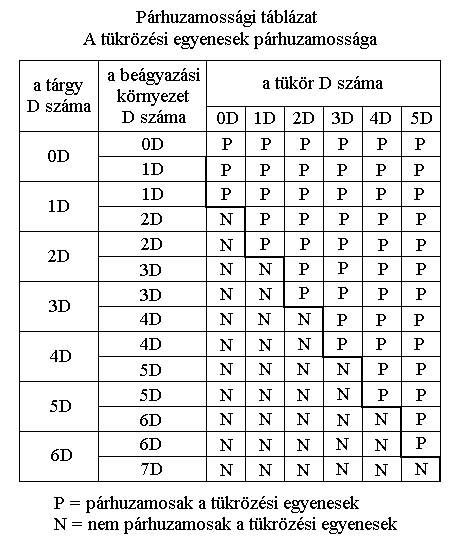
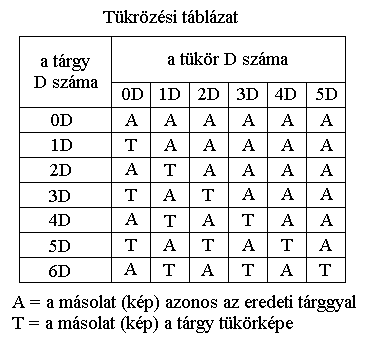
3. A TÜKRÖZÉSI TÁBLÁZAT
Vizsgáljuk meg az n dimenziós objektumok tükröződésének folyamatát változó dimenziószámú tükrök esetében, ha a beágyazási környezet dimenziószáma egyenlő a tárgy dimenziószámával.
Ha az eredeti tárgy: 0D-s (pont), a tükör pedig:
0D-s, akkor a másolata azonos lesz vele.
1D-s, akkor a másolata azonos lesz vele.
2D-s, akkor a másolata azonos lesz vele.
3D-s, akkor a másolata azonos lesz vele.
Ha az eredeti tárgy: 1D-s (szakasz), a tükör pedig:
0D-s, akkor a másolata tükörkép lesz.
1D-s, akkor a másolata azonos lesz vele.
2D-s, akkor a másolata azonos lesz vele.
3D-s, akkor a másolata azonos lesz vele.
Ha az eredeti tárgy: 2D-s (síkidom), a tükör pedig:
0D-s, akkor a másolata azonos lesz vele.
1D-s, akkor a másolata tükörkép lesz.
2D-s, akkor a másolata azonos lesz vele.
3D-s, akkor a másolata azonos lesz vele.
Ha az eredeti tárgy: 3D-s (test), a tükör pedig:
0D-s, akkor a másolata tükörkép lesz.
1D-s, akkor a másolata azonos lesz vele.
2D-s, akkor a másolata tükörkép lesz.
3D-s, akkor a másolata azonos lesz vele.
Ha az eredeti tárgy: 4D-s (hipertest), a tükör pedig:
0D-s, akkor a másolata azonos lesz vele.
1D-s, akkor a másolata tükörkép lesz.
2D-s, akkor a másolata azonos lesz vele.
3D-s, akkor a másolata tükörkép lesz.
4D-s, akkor a másolata azonos lesz vele.
Ha az eredeti tárgy: 5D-s (extratest), a tükör pedig:
0D-s, akkor a másolata tükörkép lesz.
1D-s, akkor a másolata azonos lesz vele.
2D-s, akkor a másolata tükörkép lesz.
3D-s, akkor a másolata azonos lesz vele.
4D-s, akkor a másolata tükörkép lesz.
5D-s, akkor a másolata azonos lesz vele.
Ha az eredeti tárgy: 6D-s (ultratest), a tükör pedig:
0D-s, akkor a másolata azonos lesz vele.
1D-s, akkor a másolata tükörkép lesz.
2D-s, akkor a másolata azonos lesz vele.
3D-s, akkor a másolata tükörkép lesz.
4D-s, akkor a másolata azonos lesz vele.
5D-s, akkor a másolata tükörkép lesz.
6D-s, akkor a másolata azonos lesz vele.
4. KÖVETKEZMÉNYEK
A tükrözési táblázatból látható, hogy irányfordító tükrözésről csak akkor van értelme beszélni, ha a tükör dimenziószáma kisebb a tárgy dimenziószámánál. Tükörkép, azaz fordított forgásirányú kép akkor keletkezik, ha a tükör dimenziószáma n-1, n-3, n-5 stb. a tárgy dimenziószámához képest. A különbségnek tehát páratlan számnak kell lennie. Ugyanakkor a beágyazási környezet dimenziószáma nem lehet nagyobb, mint a tárgy dimenziószáma, mert különben a tárgy és tükörképi másolata 180 fokos elforgatásokkal átvihetők egymásba és így mindig azonosak lesznek.
Gyakorlati okokból most nem foglalkozunk azokkal a speciális esetekkel, amikor a tükör és a tárgy metszik egymást (érintkeznek, fedésbe kerülnek, egymásba hatolnak). Ezek összefüggései ugyanis levezethetők a klasszikus tükrözésekből.
A tükrözés folyamatát tehát a következő paraméterek befolyásolják.:
1. A tárgy (és a beágyazási környezet) dimenziószáma, amiben a tükrözés végbemegy.
2. A tükör dimenziószáma, amin keresztül a tükrözést végrehajtjuk.
3. A tükör geometriai alakja, formája.
Időfizikai kiegészítés: Az akusztikus visszhang a közeg (levegő) rezgésének visszatérése egy hangvisszaverő felületről a forrásához. Tulajdonképpen a hang időbeli tükröződéséről van szó, mivel kétszer annyi idő múlva halljuk meg, amennyi futási (hang terjedési) távolságra van tőlünk a visszaverő felület. Ennek megfelelően az optikai tükörkép szintén az eredeti tárgy időben elcsúszott másolata, a tükröző felületről visszatérő múltbeli képe.
Biológiai kiegészítés: A tükrözés jelenségével jól magyarázhatók az olyan biológiai anomáliák, mint például a kifordított testű emberek, akiknek a belső szervei tengelyszimmetrikusan fordítva helyezkednek el. Például a szívük a jobb oldalon van. A fizikai test 3D-s, de a vezérlő kényszertere, az aura 4D-s. Ha az aurát kivetítő lélekbarion belsejében tárolódó gravitációs hullámkép valamiért 180 fokkal elfordul a 4D-ben, akkor furcsa, fordított vetületet jelenít meg a 3D-s világban. A sejtek pedig követni fogják a tanácsadótér által meghatározott helyeket az embrióban. Ezen elforgatás egyébként megfelel a középpontos tükrözésnek. A lélekbarion maga ilyenkor fizikailag nem tükröződik, különben antilélekké válva azonnal annihilálódna, amint belép a 3D-s térbe.
Azt gondolnánk, hogy a sejtosztódás, mint másolódási folyamat lehetővé teszi a tükörképi sejtek születését is, de ez a gyakorlatban nem így van, mivel az osztódás fizikailag két pont oszcillációnak felel meg. A sejtek az alkotó atomjaik tömegtehetetlensége miatt szó szerint szétrázódnak a 3D-ben és ilyenkor két azonos formájú sejt keletkezik.
5. TÜKRÖZÉSEK ÉS FORGÁSOK
Ha a tükröződési folyamat irányfordító hatású, akkor nyilvánvaló, hogy azonos eredményt kapunk a tárgy megfelelő irányú és mértékű elforgatásával is. A különféle forgásokkal és hatásaikkal részletesen foglalkozunk a Forgás n dimenzióban című írásban, ezért itt csak a tükröződést okozó elforgatásokat ismertetjük.
A forgástengely elhelyezkedhet az n dimenziós objektum kiterjedési zónáján belül (a beágyazási környezet n dimenziós) vagy kilóghat belőle (a beágyazási környezet n+1 dimenziós). Ennek megfelelően az n dimenziós tárgyat kétféleképp lehet elforgatni: n dimenzióban és n+1 dimenzióban. Az n dimenzióban elforgatott tárgyak tükörképén nem változik meg a koordináta-rendszer körüljárási iránya. Az n+1 (vagy több) dimenziós elforgatás esetén viszont félfordulatonként megváltozik a körüljárási irány.
Időfizikai kiegészítések: A 0D-s pont tükrözése egy 0D-s tükrön keresztül az 1D-s beágyazási környezetben elvileg tükörképet kellene, hogy adjon, a valóságban azonban nem ez történik. A pont ugyanis nem lehet önmaga tükörképe, mert nincsenek részei, alkotói, amik helyet cserélhetnének egymással az 1D-ben történő 180 fokos elforgatás során. Így egy balos Manduból sosem lesz jobbos.
A forgó pont önmagában szerkezet nélküli, ezért bármerre foroghat, nincs értelme az irányoknak. Attól, hogy fejjel lefelé fordítom, ugyanolyan marad, mivel a pontra nem érvényes az aszimmetria tétel, hisz teljesen szimmetrikus. Ebből következően csak egyféle pont van (a megnyilvánulatlan), ami senki számára nem létezik. A Mandu tórusz alakú geometriai modellje, amin kétféle körbejárási irány létezik ugyan tükrözhető n+1 dimenzióban elforgatva, de ez ne tévesszen meg minket. A tórusz nem pont, hanem egy sok pontból álló 3D-s geometriai alakzat, aminek felszíne van (és egy oldalú). Ugyanígy az egyes eseményhorizont rétegek is sok pontból állnak, ezért lehet belőlük kétféle csavarodású: balos vagy jobbos a forrásuk forgásának megfelelően. Az eseményhorizont, mint a pont kiterjedése már tükrözhető, mivel aszimmetrikus.
Ahogy tehát a két forgásiránynak is csak a megnyilvánulás esetén van értelme (minimum 3 pontnál), úgy a tükrözésnek is. A három pont tételnek megfelelően szükség van az eredeti pontra, a tükörképére és a szemlélőpontra, aki összehasonlítja őket és megállapítja a különbséget. De mivel egyetlen pont kvázi láthatatlan, azaz csak pontnak látható, nincs érzékelhető különbség az eredeti és a tükörképe között. Az eredeti pont eseményhorizontja és a tükörképének eseményhorizontja között viszont van.
Mindebből az a következtetés adódik, hogy egy energiakvantum vagy anyagi részecske tükrözésekor (n+1D-ben való 180 fokos elforgatásakor) az alkotó időforrásai nem válnak a korábbi önmaguk tükörképeivé. Tehát a jobbos csavarodású okforrásból készült másolati források képei (akármilyen rendszert alkotnak is) mindig ugyanolyanok maradnak. Ennek köszönhető, hogy a tükrözött rendszerek is képesek megmaradni a létezésükben, időszálaikkal felfűzve ugyanarra az Életfára. A témával részletesen az időszálak szerkezetével kapcsolatos kutatási anyagokban foglalkozunk.
Készült: 2004.03.15. - 2007.10.16.
Következő írás
Vissza a tartalomhoz