1. BEVEZETÉS
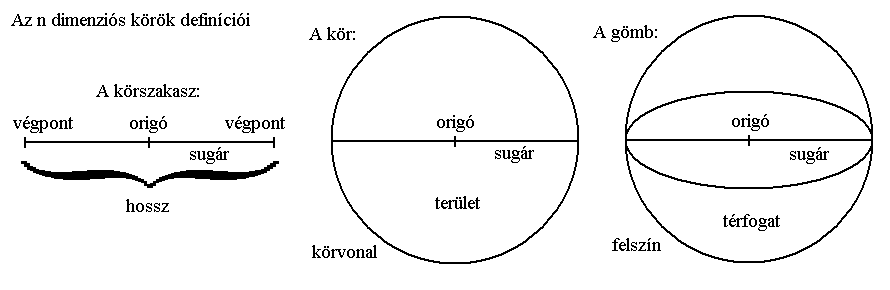
A kör (fogalmának klasszikus értelmében) azon pontok halmaza a síkban, amik egy ponttól egyenlő távolságra vannak. A körnek van origója, sugara és körvonala (határoló széle). A sugár segítségével számolható ki a kerülete és területe. A kör kerülete, széle egy 1D-s zárt görbe, míg a területe, amit elfoglal a síkban egy 2D-s véges felület.
Ha a kör definícióját kiterjesztjük más dimenziószintekre, akkor a következőket kapjuk.:
Az 1D-s szálba redukált kör (a továbbiakban körszakasz) széle két pont, amik egyforma távolságra vannak az origótól (harmadik ponttól). A három pont által lefedett szakasz, mint átmérő azonos a területtel (a továbbiakban hossz), míg a kerület (a továbbiakban végpont) két pontnyi méretű.
A 3D-s térbe kiterjesztett kör a gömb, aminek van origója, sugara, felszíne és térfogata. A gömb felszíne (területe) egy 2D-s zárt és véges felület, míg a térfogata egy 3D-s véges tér.
A 4D-s túltérbe kiterjesztett gömb a hipergömb, aminek van origója, sugara, térfogata és túltérfogata. A hipergömb térfogata (köbtartalma) egy 3D-s zárt és véges tér, míg a túltérfogata egy 4D-s véges túltér.
Ezen szabályok alapján tehát elmondhatjuk azt, amit topológiából már tudunk, hogy minden n dimenziós véges objektumnak nD-s kiterjedése és n-1D-s határa van. Az alsóbb szintű alkotók meghatározása már önkényes és nagyban függ a geometriától. Ezzel a témával részletesen az időtopológiai publikációkban foglalkozunk.
A matematikában az n dimenziós gömböt R^n hipergömbnek nevezik. Ennek topológiai dimenziója S^n-1. Ha a gömb origója a 0,0 koordinátán van és a sugara 1, akkor egységgömbnek hívják. Az alábbiakban ezt az egységgömböt fogjuk használni a különféle modellekben.
2. A LEGNAGYOBB TÁVOLSÁG A KÖRÖN
Vizsgáljuk meg az nD-s körök határán egymástól maximális távolságra lévő pontok közti távolságot az egyes dimenziószinteken. A két pont legyen A és B, amik a kör d átmérővonalának végpontjain találhatók. Eljutni A-ból B-be két módon lehet. Vagy nD-ben mozgunk, végighaladva a d-n vagy n-1D-ben mozgunk, végighaladva a körvonalon.
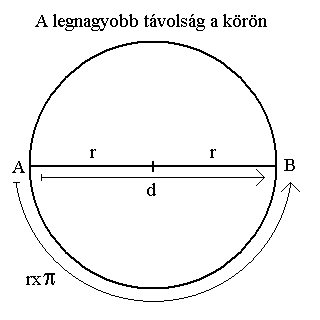
Az 1D-s körben 1D-ben mozogva 2xr távolságot kell megtennünk, míg 0D-ben mozogva 0 a távolság. Ez azt jelenti, hogy tényleges fizikai mozgás nélkül lehet egyik pontból áthelyeződni a másikba, tehát a két pont gyakorlatilag egy helyen van. Ha az 1D-s kört, mint szakaszt egy fizikai időszál modelljének tekintjük, akkor azonnal nyilvánvaló, hogy a szál végpontjai egy időben léteznek, és köztük minden állapotváltozás, azaz információ gyakorlatilag késedelem nélkül átadódik. Ez a késedelem nélküli kommunikáció működésének szemléletes bizonyítása. A modell részletes kifejtése az időszálak szerkezetével kapcsolatos publikációkban olvasható.
A 2D-s körben 2D-ben mozogva (ami lényegében csak 1D-s útvonalat jelent) 2xr távolságot kell megtennünk, míg 1D-ben mozogva rxPi (fél kerületnyi) a távolság. Egységnyi sugarú kör esetén ez azt jelenti, hogy 2D-ben a távolság 2, 1D-ben pedig 3,1415.
A 3D-s gömbben 3D-ben mozogva (ami lényegében csak 1D-s útvonalat jelent) 2xr távolságot kell megtennünk, míg 2D-ben mozogva (ami lényegében ugyanúgy csak 1D-s útvonalat jelent) rxPi a távolság. A kettő különbsége tehát nem változik. Az összes magasabb dimenziószámú kör esetében ugyanez lesz a helyzet.
A jelenség hasznosításának egy szemléletes módja lenne, ha tudnánk olyan űrhajót építeni, ami képes n+1D-be kiugorva közlekedni a világűrben, vagyis a 3D-s távolságot a 4D-ben tenné meg. A különbség csak 1,1415, de ez már lehetővé teszi, hogy a jármű relatív sebessége a 3D irányából nézve 3/2-szeresére gyorsuljon. Ezen a módon elvileg átléphető lenne a fénysebesség anélkül, hogy a korlátozó fizikai törvényeket megszegnénk. A témával részletesebben a térugrással és a téridő szerkezetével kapcsolatos publikációkban foglalkozunk.
3. ELNEVEZÉSEK
Mielőtt tovább mennénk, alkossunk néhány szakkifejezést, amik révén egyértelműen tudunk utalni az egyes dimenziószinteken megnyilvánuló tulajdonságokra. A magyar nyelvben szerencsére megfigyelhetők bizonyos szabályosságok, amik megkönnyítik a dolgunkat, így érdemes felhasználni őket a szóalkotáshoz. Ehhez nagy segítséget és ötleteket nyújtott Varga Csaba - A kőkor élő nyelve (Fríg Kiadó, 2003.) című munkája, melyben a magyar nyelv fraktális szerkezetét ismerteti.
A felsőbb tereket és objektumaikat a matematikában egyszerűen a hiper (túlzó, túlságos) előtaggal szokták megnevezni, függetlenül a dimenziószámuktól. Mivel az általunk fejlesztett n dimenziós időmatematikában gyakorta foglalkozunk a felsőbb terek szerkezetével, a könnyebb szóhasználat érdekében külön neveket adtunk az egyes dimenziószinteknek (praktikusan csak 6D-ig).
Ennek megfelelően a 4D-s terek és objektumaik megtartják a hiper előtagot, amit magyarul túltérnek nevezünk. A lelkek a fizikai test halála után a túlvilágra kerülnek, a 3D-s teret elhatároló szeparátorok túloldalára, ami a gyakorlatban megfelel a 4D-s téridőnek. Itt van a mennyország, túl a mi világunk kiterjedésén, de elérhető közelségben.
Az 5D-s terek kapják az extra (valamin kívüli) előtagot, amit magyarul kültérnek nevezünk. A monász téridőben (egy térhatosban) ez alkotja a legkülső kiterjedési zónát, a külvilágot. Mivel a Naprendszert szeparáló térbúra csak a 4D-ig gátolja a lelkek (és űrhajók) közlekedését a csillagközi tér irányába, Solariát akadály és térugrás nélkül elhagyni csak az 5D irányában lehet a külvilág (külföld, külhon) felé.
A 6D-s terek kapják az ultra (szélsőséges) előtagot, amit magyarul feltérnek nevezünk (a széltér, szélsőtér helyett, mert a szél 1D-s). A triász téridőben (három térhatosban) ez alkotja a legfelső természetes kiterjedést, a felvilágot. Az univerzumunk világtojását kormányzó isteni intelligenciák világa ez, ahová csak a legképzettebb sámánok és beavatottak juthatnak el az Életfán, Égig érő fán "felmászva" a felső világba.
Az ennél magasabb dimenziószámú kiterjedésekre az egyszerűség kedvéért az "nD-s felsőtér" kifejezést használjuk. Az n-1D-t altérnek (infratér), az n+1D-t felsőtérnek (ultratér) is nevezzük egyes esetekben. A felsőtér nem tévesztendő össze a feltérrel.
Fontos, hogy az itt használt hiper szót ne keverjük össze az időfizikában és a térugrásos űrhajózásban már korábban elterjedt jelentésével, ahol a hipertér nem a 4D-s túltéridőt jelenti (a mi 3D-s világunk felsőterét), hanem a mi térhatosunkkal párhuzamosan és felváltva létező, túlsó térhatosban vagy térhatosokban található 4D-s túltéridőket.
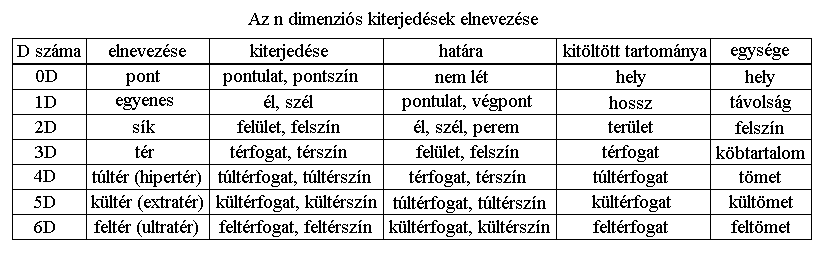
Minden véges méretű objektum kitölt egy nD-s tartományt és van egy n-1D-s határa, ami elválasztja a környezetétől. Az alábbiakban ezen objektumoknak és részeiknek az egyes dimenziószinteken használatos praktikus elnevezései következnek.:
A 0D-s kiterjedés a pont, amiben a 0D-s véges objektumoknak van 0D-s nem léte (megnyilvánulatlansága, mivel a -1D mint kiterjedés nem értelmezhető) és 0D-s pontulata, pontszíne (röviden: pontja) azaz léte (megnyilvánulása).
Az 1D-s kiterjedés az egyenes, amiben az 1D-s véges objektumoknak van 0D-s pontulata (pontszíne) és 1D-s élülete, élszíne (röviden: éle). Mozgó (mindkét irányba nyúló vagy zsugorodó) szakasz esetén a pontokat végpontoknak hívjuk, irányított szakasz esetén pedig csúcspontnak és mélypontnak.
A 2D-s kiterjedés a sík, amiben a 2D-s véges objektumoknak van 1D-s széle (éle, pereme) és 2D-s felülete, felszíne (röviden: fele).
A 3D-s kiterjedés a tér, amiben a 3D-s véges objektumoknak van 2D-s felülete (felszíne) és 3D-s térfogata, térszíne (röviden: tere).
A 4D-s kiterjedés a túltér (hipertér), amiben a 4D-s véges objektumoknak van 3D-s térfogata (térszíne) és 4D-s túltérfogata (hiperfogata), túltérszíne (hiperszíne), röviden: túltere.
Az 5D-s kiterjedés a kültér (extratér), amiben az 5D-s véges objektumoknak van 4D-s túltérfogata (túltérszíne) és 5D-s kültérfogata (extrafogata), kültérszíne (extraszíne), röviden: kültere.
A 6D-s kiterjedés a feltér (ultratér), amiben a 6D-s véges objektumoknak van 5D-s kültérfogata (kültérszíne) és 6D-s feltérfogata (ultrafogata), feltérszíne (ultraszíne), röviden: feltere.
A 0D-s véges objektumok által kitöltött tartományt hívjuk (pontnyi) helynek.
Az 1D-s véges objektumok által kitöltött tartományt hívjuk (szakasznyi) hossznak.
A 2D-s véges objektumok által kitöltött tartományt hívjuk területnek.
A 3D-s véges objektumok által kitöltött tartományt hívjuk térfogatnak.
A 4D-s véges objektumok által kitöltött tartományt hívjuk túltérfogatnak.
Az 5D-s véges objektumok által kitöltött tartományt hívjuk kültérfogatnak.
A 6D-s véges objektumok által kitöltött tartományt hívjuk feltérfogatnak.
A kiterjedés hiányát a ponttal (hellyel) határozzuk meg.
A hosszúságot egységnyi szakaszokkal (távolsággal) határozzuk meg.
A területet egységnyi négyzetekkel (felszínnel) határozzuk meg.
A térfogatot egységnyi kockákkal (köbtartalommal) határozzuk meg.
A túltérfogatot egységnyi hiperkockákkal (tömettel, túltömettel) határozzuk meg.
A kültérfogatot egységnyi extrakockákkal (kültömettel) határozzuk meg.
A feltérfogatot egységnyi ultrakockákkal (feltömettel) határozzuk meg.
A tömet (töltet) szót a régi magyar nyelvből vettük, mivel jobban illett a logikai rendszerbe, mint a tartalom (űrtartalom) szó.
Vegyük észre, hogy amennyiben a felület két oldalú, úgy a nyelvünkből hiányzik a másik oldalára (aljára) használható alulat kifejezés. Ugyanígy a felszín (felső oldal) párja, az alszín (alsó oldal) sem használatos. Helyettük használjuk a fele (felső része) és alfele (alsó része) szavakat, valamint a visszáját a szabászatban. Ennek az az oka, hogy az érzékelésünk (látásunk és tapintásunk) egyszerre mindig csak a dolgok egyik oldalát képes érzékelni geometriai okokból. A témát részletesen lásd az Érzékelés n dimenzióban című írásunkban.
Ha látom egy tárgy külsejét, felszínét, akkor nem látom a belsejét, alszínét. Ha kifordítom (a visszájára), akkor látom, de szubjektíve nekem akkor az lesz a felszín. A felszín a dolgoknak mindig az a fele, amit éppen látok, észlelek (színesben, mert a színem előtt van). Így elég egyoldalú az érzékelésünk a 3D-s világban, s ennek megfelelően a gondolkodásunk is, ami hozzá igazodik.
Például az emberi test a 3D-ben tömör objektumnak látszik a számunkra, ezért csak felszíne, külseje van. Emiatt a testünk két oldalára (bal és jobb felére) gyakran úgy utalunk, hogy fél oldal. Matematikailag viszont a fél oldal nem értelmezhető fogalom.
Az észlelés módjának döntő szerepe van a világról alkotott gondolatrendszereink, modelljeink kialakításában, s persze a mindennapi életünket is alapvetően meghatározza. Mivel egy szemlélőpontból (1 helyről) nem lehet egyszerre (1 időben) mindkét oldalát érzékelni egy kiterjedt objektum felszínének (közvetlenül, tükrözés és egyéb trükközés nélkül), ezért nyilvánvaló, hogy a számunkra tulajdonképpen minden dolognak csak egy oldala van a világban. Az az oldal, amelyiken éppen állunk. Ezért vagyunk elfogultak. A két vagy több oldalúság ideája csupán képzetes jelenség, amit a tapasztalataink értelmezése során hoztunk létre, fogalomalkotás révén. Erre egyébként a felszín fogalmának mélyebb időtopológiai elemzése is rávilágított, amivel ott (Időtopológia) foglalkozunk.
Egyszerre mindkét oldalát észlelni egy felületnek nyilvánvaló ellentmondás lenne bármely szemlélő számára, így ennek feloldása érdekében a szemlélőnek fel kellene hasadnia (ezt hívják a pszichológiában skizofréniának). Nyilván ezért olvasható egyes teremtésmitológiákban, hogy az Isten, az első teremtő szellem önmagát darabokra szakította. Sok darabra esett szét, amik kiszóródtak a világegyetembe és minden élőlénybe jutott belőlük egy kis darabka. Az Isten tehát a lelkek (szemlélők) összessége fizikailag. Ezzel a témával is más publikációkban foglalkozunk részletesen.
4. A KÖR SZÉLE
Egy klasszikus 2D-s körnek van széle, ami a síkban elhatárolja a területét a beágyazási környezetétől. Vajon lehet-e készíteni olyan kört, aminek nincs határoló széle, bár véges méretű a sugara? Ez csak a beágyazási környezet dimenziószámától és geometriájától függ.
Rajzoljunk egy kis kört egy nagyobb gömbfelületre. Ha addig növeljük a kör sugarát, míg eléri a gömb kerületének negyedét, a kör kerülete eléri a maximumát. Ha tovább növeljük a sugarat, a kerület már csökkenni fog, mígnem eléri a gömb túloldalát és ponttá zsugorodva gyakorlatilag eltűnik. A 2D-s kör területe azonossá válik a 3D-s gömb felületével, sugara pedig egyenlő a gömb kerületének felével.
A gömbfelületi kör lokálisan 2D-s, ezért nincs széle a síkban, bár a területe véges. Emiatt azonos a beágyazási környezetével, amit teljesen kitölt. Globálisan viszont 3D-s, tehát van széle a térben, amit felületnek nevezünk. Ez a térben elhatárolja a térfogatát a beágyazási környezetétől.
A szabály természetesen kiterjeszthető a felsőbb és alsóbb dimenziószámú körökre is a következőképpen.:
Az 1D-s körszakasz az 1D-ben globálisan rendelkezik határoló széllel (pontulattal), lokálisan viszont azonos egy szél (nem lét) nélküli 0D-s ponttal.
A 2D-s körvonal a 2D-ben globálisan rendelkezik határoló széllel (éllel, peremmel), lokálisan viszont azonos egy szél (pontulat) nélküli 1D-s körszakasszal.
A 3D-s gömbfelszín a 3D-ben globálisan rendelkezik határoló széllel (felülettel), lokálisan viszont azonos egy szél (él, perem) nélküli 2D-s körrel.
A 4D-s hipergömbtérfogat a 4D-ben globálisan rendelkezik határoló széllel (térfogattal), lokálisan viszont azonos egy szél (felület) nélküli 3D-s gömbbel.
Az 5D-s extragömbtúltérfogat az 5D-ben globálisan rendelkezik határoló széllel (túltérfogattal), lokálisan viszont azonos egy szél (térfogat) nélküli 4D-s hipergömbbel.
A 6D-s ultragömbkültérfogat a 6D-ben globálisan rendelekzik határoló széllel (kültérfogattal), lokálisan viszont azonos egy szél (túltérfogat) nélküli 5D-s extragömbbel.
Most fogalmazzuk meg ugyanezt a szabályt kicsit másképpen, abból a szempontból vizsgálva a kérdést, hogy egy nD-s körön milyen n-1D-s körök helyezhetők el.
Az 1D-s tömör körszakaszon kétféle 0D-s kör helyezhető el: a három pontú kör (benne), és az origó nélküli, két pontból álló körszakasz, ami azonos a körszakasz végpontjaival.
A 2D-s tömör körlapon kétféle 1D-s kör helyezhető el: a körszakasz (benne), ami azonos az átmérővonallal, és maga a körvonal, ami azonos a kör szélével (peremével).
A 3D-s tömör gömbön kétféle 2D-s kör helyezhető el: a sík körlap (benne), és maga a gömbfelület, ami azonos a gömb felszínével.
A 4D-s tömör hipergömbön kétféle 3D-s gömb helyezhető el: a 3D-s gömb, aminek van felszíne, és maga a hipergömbtérfogat, ami azonos az önmagába visszakanyarodó 3D-s gömbbel.
Az 5D-s tömör extragömbön kétféle 4D-s hipergömb helyezhető el: a 4D-s hipergömb, aminek van térfogata, és maga az extragömbtúltérfogat, ami azonos az önmagába visszakanyarodó 4D-s hipergömbbel.
A 6D-s tömör ultragömbön kétféle 5D-s extragömb helyezhető el: az 5D-s extragömb, aminek van túltérfogata, és maga az ultragömbkültérfogat, ami azonos az önmagába visszakanyarodó 5D-s extragömbbel.
5. A KÖR OLDALA
Most vizsgáljuk meg az nD-s körök szélét topológiailag abból a szempontból, hogy hány oldaluk van. Az oldal a szélnek az a tulajdonsága, hogy a beágyazási környezetét két nem összefüggő részre képes határolni. Az egyoldalú szél nem határolja két részre a környezetet, csak a két oldalú. A témával bővebben az Időtopológia című publikációban foglalkozunk.
A 0D-s pontnak nincs kiterjedése, ennél fogva nincs belseje sem. Csak külseje van, tehát egyoldalú - a jelenlegi (hivatalos) topológiai modellek szerint. Hogy ez vajon igaz-e, az rövidesen kiderül, de előbb menjünk tovább a magasabb dimenziószintekre.
Az 1D-s körszakasz ha üres, akkor három pontú körnek hívjuk. Ennek a széle két pont (végpontok), amik 0D-sek. Ezek az 1D-s kiterjedést (szálat) három részre osztják. Egy belső szakaszra és két nem érintkező (kvázi végtelen) félegyenesre. A három pontú körnek tehát három oldala van: egy belseje és két külseje. A hivatalos topológiai modellekben nem szerepelnek három oldalú objektumok, de az időtopológiai modelljeinkben már találkoztunk velük, lásd a szalagológiai publikációkat (a 2004-es év anyagai között).
A tömör körszakasz széle szintén két pont, amik 0D-sek, de ez az 1D-s kiterjedést csak két részre osztja, mert nincs belső szakasza. Tehát úgy viselkedik, mint egy pont a szálon (azzal ekvivalens ebben a topológiai értelmezésben), mert csak két oldala van: két külseje.
A 2D-s kör ha üres, akkor körvonalnak hívjuk. Ennek a széle egy zárt görbe, ami 1D-s. Ez a 2D-s kiterjedést (síkot) két részre osztja: kintre és bentre, ezért két oldala van: külseje és belseje.
A tömör körlap széle szintén egy zárt görbe, ami 1D-s, de ez a 2D-s kiterjedést nem osztja két részre, mert nincs belseje. Tehát úgy viselkedik, mint egy pont a szálon, de csak egy oldala van: külseje.
A 3D-s gömb ha üres, akkor gömbfelületnek (labdának) hívjuk. Ennek a széle egy zárt felület, ami 2D-s. Ez a 3D-s kiterjedést (teret) két részre osztja: kintre és bentre, ezért két oldala van: külseje és belseje.
A tömör gömb (golyó) széle szintén egy zárt felület, ami 2D-s, de ez a 3D-s kiterjedést nem osztja két részre, mert nincs belseje. Tehát úgy viselkedik, mint egy pont a szálon és csak egy oldala van: külseje.
A 4D-s hipergömb ha üres, akkor hipergömbtérfogatnak hívjuk. Ennek a széle egy zárt tér, ami 3D-s. Ez a 4D-s kiterjedést (túlteret) két részre osztja: kintre és bentre, ezért két oldala van: külseje és belseje.
A tömör hipergömb széle szintén egy zárt tér, ami 3D-s, de a 4D-s kiterjedést nem osztja két részre, mert nincs belseje. Tehát úgy viselkedik, mint egy pont a szálon és csak egy oldala van: külseje.
Az 5D-s extragömb ha üres, akkor extragömbtúltérfogatnak hívjuk. Ennek a széle egy zárt túltér, ami 4D-s. Ez az 5D-s kiterjedést (külteret) két részre osztja: kintre és bentre, ezért két oldala van: külseje és belseje.
A tömör extragömb széle szintén egy zárt túltér, ami 4D-s, de az 5D-s kiterjedést nem osztja két részre, mert nincs belseje. Tehát úgy viselkedik, mint egy pont a szálon és csak egy oldala van: külseje.
A 6D-s ultragömb ha üres, akkor ultragömbkültérfogatnak hívjuk. Ennek a széle egy zárt kültér, ami 5D-s. Ez a 6D-s kiterjedést (felteret) két részre osztja: kintre és bentre, ezért két oldala van: külseje és belseje.
A tömör ultragömb széle szintén egy zárt kültér, ami 5D-s, de a 6D-s kiterjedést nem osztja két részre, mert nincs belseje. Tehát úgy viselkedik, mint egy pont a szálon és csak egy oldala van: külseje.
A fenti meghatározásokból azonnal nyilvánvaló lesz több érdekes ellentmondás. Vegyük sorra őket, hátha tisztázhatók értelemmel.
Ha a szél oldalszámát meghatározó szabály minden dimenziószinten érvényes, akkor az 1D-ben a három pontú kör a szálat nem három, hanem csak két részre osztja. Egy belső szakaszra és egy külső egyenesre. Vagyis az 1D-s szál nem lehet valódi, abszolút egyenes, hanem csakis relatív egyenes, méghozzá egy kör. Tekinthetjük kvázi végtelen kerületi hosszúságú körnek. Így a három pontú körnek csak két oldala van valójában. A tömör körszakasz pedig nem osztja két részre az 1D-s kiterjedést, tehát csak egy külseje van. Ez a modell jól illeszkedik az Elmélkedések a végtelenről című írásban (lásd: a 2006-os év anyagait) ismertetett számkörhöz, valamint az időfizikai modelljeinkben szereplő nyúló időszálhoz és a hermetikus filozófia önmagába zárt létezésének matematikai leképzéséhez.
Ha a pont nulla helyet foglal el a beágyazási környezetéből (szálból), akkor a tömör körszakasz, mint véges kiterjedés sem foglal el semennyit a kvázi végtelen egyenesből. Ha a körszakasz két végén lévő pontok (a kerületi pontok) között nincs tényleges távolság (szomszédosak), akkor fizikailag az időszál két végén lévő pontok között sincs. Így viszont az időszál tényleges hossza kívülről nézve mindig nulla. Belülről nézve pedig végesen nagy, ami a szál mozgása, időbeli kiterjedése okán egyre nyúlik, bővül a végtelenségig.
Ez egyenértékű azzal a létfilozófiai felismeréssel, miszerint a létezés kívülről szemlélve mindig nulla méretű. Kívülről persze nem lehet szemlélni a létezést, ami önmagába zárt jelenség, ezért csak belülről értelmezhetők és észlelhetők a tartalmi különbségei (struktúrája). Ha viszont az n elemű létezés csak belülről szemlélhető, a létező csak belülről képes önmagát érzékelni (n-1D-snek) . Akkor pedig a szél oldalszámát meghatározó szabálynak a 0D-s pontra is érvényesnek kell lennie. Vagyis kétféle pont létezik, nem csak egy. Lássuk tehát, hogy kell kinéznie a ponttal kapcsolatos definícióinknak helyesen.:
A 0D-s pont ha üres, akkor megnyilvánuló pontnak hívjuk. Ennek a széle egy zárt pont, ami 0D-s. Ez a 0D-s (nem) kiterjedést (pontot) két részre osztja: kintre és bentre, ezért két oldala van: külseje és belseje.
A tömör pont széle szintén egy zárt pont, ami 0D-s, de ez a 0D-s (nem) kiterjedést nem osztja két részre, mert nincs belseje. Tehát csak egy oldala van: külseje.
A megnyilvánuló pontot régi nevén Bindunak hívjuk (az időfizikában). A Bindu két pontból áll (ezt hívjuk fentebb: egy zárt pontnak), amik külön és együtt is 0D-sek, mivel az 1D-s kiterjedés minimális hossza (a három pont tételből következően) három pontnyi (lásd: külön publikációban). Ezért képes a puszta létezést (a 0D-s nem kiterjedést) két részre osztani: kintre és bentre, amit hagyományosan a két oldalú időgömbbel (múltszférával) ábrázolunk geometriailag.
A tömör pont a létezést nem osztja két részre (mert nincs belseje), ezért úgy viselkedik, mint a megnyilvánulatlan. Ezt régi nevén Mandunak hívjuk (az időfizikában). Mindez gyönyörűen egybevág a korábbi időfizikai és létfilozófiai modelljeinkkel és matematikai oldalról is megerősíti őket. Most pedig lássuk a körszakasszal kapcsolatos definícióinkat helyesen.:
Az 1D-s körszakasz ha üres, akkor három pontú körnek hívjuk. Ennek a széle egy zárt pont (két végpont), ami 0D-s. Ez az 1D-s kiterjedést (szálat) két részre osztja: kintre és bentre, ezért két oldala van: külseje és belseje.
A tömör körszakasz széle szintén egy zárt pont (két végpont), ami 0D-s, de ez az 1D-s kiterjedést nem osztja két részre, mert nincs belseje. Tehát úgy viselkedik, mint egy pont a szálon, mert csak egy oldala van: külseje.
A tömör objektumok tehát - a dimenziószámuktól függetlenül - topológiailag egyenértékűek a ponttal, mert egy oldalúak, míg az üres objektumok a körvonallal egyenértékűek, ami két oldalú. Ebben az írásban nem foglalkozunk mélyebben a kétoldalúság időtopológiai értelmezésével, ami némileg árnyalja ezt a meghatározást, mivel nem akartuk túlbonyolítani a rendszert. De feltétlenül ajánljuk, hogy az Időtopológia című írásban lefektetett szabályokat (a kétoldalúsággal kapcsolatban) feltétlenül alkalmazza az Olvasó a fentiekre is gondolatban.
Felmerül a kérdés, hogyan kaphatunk a pontból, mint a legegyszerűbb objektumból (elemből) egy kört, aminek görbéje (körvonala) több pontból áll?
Ha a pont időben létezik (Bindu: tehát két pont valójában), akkor csak egy módon mozoghat a saját kiterjedés nélküli, 0D-s beágyazási környezetében: forog a tengelye körül. A forgástengely iránya (ami kilóg a beágyazási környezetből, mert a tengely egy egyenes, tehát 1D-s) bármilyen lehet. A forgás iránya egy tengely körül kétféle lehet: balos vagy jobbos, bár az irányultság csak minimálisan három pont esetén értelmezhető (lásd a forgással kapcsolatos korábbi publikációkat).
Ha a pont (Bindu) az időben létezve és mozogva nem a saját tengelye körül forog, hanem egy másik, rajta kívül létező (harmadik) ponton átmenő tengelyt jár körül, akkor kering. A mozgásának útvonala tehát egy körvonal lesz (minimálkör, lásd: A három pont tétel című írásban).
Egy pont csak akkor létezik, ha (legalább) egy másik pont számára létezik. A létezés pedig, mint időbeli folyamat csak akkor értelmezhető, ha mozgással, változással jár együtt. A létezésben keletkező legegyszerűbb megnyilvánulás, forma, kiterjedéssel rendelkező objektum tehát (törvényszerűen) a kör, s nem az egyenes. Az egyenes a kör vonalának egy tetszőlegesen kicsiny részéből képezhető a megfelelő szemléletmód kialakításával. Egy külső szemlélő számára ugyanis a realizáció késedelme miatt egy kvázi végtelen átmérőjű kör vonalának észlelete az egyenes illúzióját adja, ami a két vége felé elnyúlik a végtelenbe.
6. RÁLÁTÁS A KÖRRE
Egy n dimenziós véges rendszert alapvetően kétféle dimenziószámú beágyazási környezetből érdemes szemlélni és vizsgálni a tulajdonságait. Az egyik a vele megegyező dimenziószámú közeg, a másik az n+1D-s közeg. Az alábbiakban ezeket a rálátási módokat soroljuk fel két variációban: ha tömör és ha üres az objektum.
Első sorozat: az nD-s beágyazási környezetbe helyezett szemlélő tapasztalatai.:
A 0D-s pont ha tömör (megnyilvánulatlan) akkor egyoldalú, ha üres (megnyilvánuló) akkor kétoldalú. A 0D-s beágyazási környezetéből szemlélve körbejárható, de falának (nem létének) átszakítása nélkül nem lehet belejutni, hogy belülről is szemlélhető legyen, vagyis zártnak tekintjük.
Az 1D-s szakasz ha tömör (folytonos) akkor egyoldalú, ha üres (három pontú kör) akkor kétoldalú. Az 1D-s beágyazási környezetéből szemlélve körbejárható (mert az egyenes valójában kör), de falának (végpontjainak) átszakítása nélkül nem lehet belejutni, hogy belülről is szemlélhető legyen, vagyis zártnak tekintjük.
A 2D-s kör ha tömör (körlap) akkor egyoldalú, ha üres (körvonal) akkor kétoldalú. A 2D-s beágyazási környezetéből szemlélve körbejárható, de falának (szélének, peremének) átszakítása nélkül nem lehet belejutni, hogy belülről is szemlélhető legyen, vagyis zártnak tekintjük.
A 3D-s gömb ha tömör (golyó) akkor egyoldalú, ha üres (labda) akkor kétoldalú. A 3D-s beágyazási környezetéből szemlélve körbejárható, de falának (felületének) átszakítása nélkül nem lehet belejutni, hogy belülről is szemlélhető legyen, vagyis zártnak tekintjük.
A 4D-s hipergömb ha tömör akkor egyoldalú, ha üres akkor kétoldalú. A 4D-s beágyazási környezetéből szemlélve körbejárható, de falának (térfogatának) átszakítása nélkül nem lehet belejutni, hogy belülről is szemlélhető legyen, vagyis zártnak tekintjük.
Az 5D-s extragömb ha tömör akkor egyoldalú, ha üres akkor kétoldalú. Az 5D-s beágyazási környezetéből szemlélve körbejárható, de falának (túltérfogatának) átszakítása nélkül nem lehet belejutni, hogy belülről is szemlélhető legyen, vagyis zártnak tekintjük.
A 6D-s ultragömb ha tömör akkor egyoldalú, ha üres akkor kétoldalú. A 6D-s beágyazási környezetéből szemlélve körbejárható, de falának (kültérfogatának) átszakítása nélkül nem lehet belejutni, hogy belülről is szemlélhető legyen, vagyis zártnak tekintjük.
Második sorozat: az n+1D-s beágyazási környezetbe helyezett szemlélő tapasztalatai.:
A 0D-s pont ha tömör (megnyilvánulatlan) akkor egyoldalú, ha üres (megnyilvánuló) akkor kétoldalú. Az 1D-s beágyazási környezetéből szemlélve körbejárható a 0D-ben és az 1D-ben is. A falának (nem létének) átszakítása nélkül is bele lehet jutni az 1D felől, hogy belülről is szemlélhető legyen, vagyis nyitottnak tekintjük.
Az 1D-s szakasz ha tömör (folytonos) akkor egyoldalú, ha üres (három pontú kör) akkor kétoldalú. A 2D-s beágyazási környezetéből szemlélve körbejárható az 1D-ben és a 2D-ben is. A falának (végpontjainak) átszakítása nélkül is bele lehet jutni a 2D felől, hogy belülről is szemlélhető legyen, vagyis nyitottnak tekintjük.
A 2D-s kör ha tömör (körlap) akkor egyoldalú, ha üres (körvonal) akkor kétoldalú. A 3D-s beágyazási környezetéből szemlélve körbejárható a 2D-ben és a 3D-ben is. A falának (szélének, peremének) átszakítása nélkül is bele lehet jutni a 3D felől, hogy belülről is szemlélhető legyen, vagyis nyitottnak tekintjük.
A 3D-s gömb ha tömör (golyó) akkor egyoldalú, ha üres (labda) akkor kétoldalú. A 4D-s beágyazási környezetéből szemlélve körbejárható a 3D-ben és a 4D-ben is. A falának (felületének) átszakítása nélkül is bele lehet jutni a 4D felől, hogy belülről is szemlélhető legyen, vagyis nyitottnak tekintjük.
A 4D-s hipergömb ha tömör akkor egyoldalú, ha üres akkor kétoldalú. Az 5D-s beágyazási környezetéből szemlélve körbejárható a 4D-ben és az 5D-ben is. A falának (térfogatának) átszakítása nélkül is bele lehet jutni az 5D felől, hogy belülről is szemlélhető legyen, vagyis nyitottnak tekintjük.
Az 5D-s extragömb ha tömör akkor egyoldalú, ha üres akkor kétoldalú. A 6D-s beágyazási környezetéből szemlélve körbejárható az 5D-ben és a 6D-ben is. A falának (túltérfogatának) átszakítása nélkül is bele lehet jutni, hogy belülről szemlélhető legyen, vagyis nyitottnak tekintjük.
A 6D-s ultragömb ha tömör akkor egyoldalú, ha üres akkor kétoldalú. A 7D-s beágyazási környezetéből szemlélve körbejárható a 6D-ben és a 7D-ben is. A falának (kültérfogatának) átszakítása nélkül is bele lehet jutni, hogy belülről szemlélhető legyen, vagyis nyitottnak tekintjük.
A szabály, amit megállapíthatunk a fentiek alapján az, hogy ami nD-ben szemlélve zártnak látszik, az n+1D-ben nyitottnak. Fontos következménye ennek a létfilozófiában, hogy az nD-s minden létezőben található szemlélők (az Isten, a lelkek) nem láthatják át sosem az egészet a maga teljes komplexitásában. Nem képesek mindenbe belelátni (korlátlanul a dolgok mélyére látni), mert ahhoz kellene egy n+1D-s beágyazási környezet, azaz egy külső szemlélőpont. Mivel pedig a szemlélőpont (jelen) önmagát sosem látja, ezért maximum n-1D-s látásmódra képes az egészben.
Ennek a látásmódnak köszönhető, hogy a létező (Isten) vég nélkül gyártja magában (magából, magának) az újabb forráspontokat (helyeket), hogy általuk (rajtuk keresztül) szemlélődve jobban megismerhesse önmagát. Ennek a folyamatnak (teremtésnek) tehát (matematikailag indokolhatóan) sosem lesz vége, mivel csak ezáltal gyarapíthatja a saját információ tartalmát a rendszer (ami mozgásban és ezáltal életben tartja az egészet).
Készült: 2004.05.17. - 2006.07.17.
Következő írás
Vissza a tartalomhoz