1. A RUGALMASSÁG
A hangok és mindenféle rezgések, lökéshullámok terjedése egy részecskékből, atomokból álló közegben fizikailag úgy modellezhető szemléletesen, mint a rugalmas golyók ütközése. A rezgés terjedési sebessége így a golyók sűrűségétől és rugalmasságától függ. Minél sűrűbb a közeg, annál kisebb lökések képesek tovább adódni benne. Minél rugalmasabbak a golyók, annál gyorsabban elnyelődik bennük a lökés, mert energiája a golyók deformálására fordítódik ahelyett, hogy tovább adódna.
Felmerül a kérdés, hogy mi lehet a rugalmasság fizikailag? Mert azt tudjuk, hogy az atomokat alkotó részecskék valójában soha nem érintkeznek egymással közvetlenül. A belőlük áradó longitudinálisan modulált hullámterek taszító hatása az, ami közvetíti a kölcsönhatásokat, az elmozdulást és a deformációt előidézve. Ez a hullámtér dinamikusan változó, forgó és igen nagy frekvenciájú, aminek szerkezete a kibocsátó forrásától függ. Tehát felismerhetően másmilyen tere van a neutronnak, a protonnak, az elektronnak és a fotinónak. A nagy magnukleonok hullámai jóval erősebbek az elektronok hullámterénél, amik viszont gyorsabban mozognak náluk. A fénykvantumok hullámtere pedig egyenként igen gyenge, de csoportosan nagy hatást képesek gyakorolni a részecskék tartályaira. A fény mennyisége alapján határozzuk meg a gerjesztettségi szintet, hétköznapi nevén a hőmérsékletet.
Az atomok között kialakuló első és másodrendű kötések az erejükben és távolságukban, valamint a darabszámukban különböznek egymástól. Ha a legkülső stabil elektron pályája alapján határozzuk meg az atom felszínét, átmérőjét, akkor a gömbszerű atomok laza érintkezését tekinthetjük másodrendű kötésnek, míg az egymásba merülő atomok kapcsolatát elsőrendű kötésnek. Ez persze csak leegyszerűsített modellje a jóval bonyolultabb valóságnak.
Ennek megfelelően a rugalmasság nem más, mint az egymás hullámterében tartózkodó részecskék holtjátéka, lötyögése a kényszertérben, ami megtartja őket a térbeli pozíciójukban. Ha a hullámtéri potenciálgödör szoros (szűk) és a térben mereven helyezkedik el a forrásához képest, az anyag makroszinten keménynek és merevnek mutatkozik. Nehéz deformálni, viszont könnyű eltörni a ridegsége miatt. A rugalmatlan közegben ezért jól terjednek a rezgéshullámok, hisz a részecskék képtelenek kitérni a szomszédaik lökése elől, muszáj tovább adniuk a kapott impulzust.
2. A HANGOK
Az álló levegőnek és víznek azért nincs hangja, mert az atomok alig mozognak egymáshoz képest. Jobbára csak lökdösik, tuszkolgatják a szomszédaikat, a nyomástól függően kissé egymásba hatolva elektronhéjaikkal, illetve elgördülve egymáson. Így bár a közeg mozog, a mikrorezdülések kiegyenlítik egymást és az emberi fül számára nincs észlelhető erősségű hang benne.
Az atomok ezen természetes lökdösődéséből fakadó zajnak (hőzajnak) köszönhető, hogy nem lehet bármilyen halk hangot előidézni egy anyagi közegben. Ahol sosincs igazi csend, csupán a hallhatóság szintje alá esik a zaj mértéke. Ezért nem lehet a mikrofonok érzékenységét sem tetszőlegesen fokozni, erősíteni, mert végül beleütközünk magának a vevőmembránnak a saját hőzaja keltette sistergés falába (ez az egészséges fülzúgás oka ha nagy a csend). Abszolút csönd tehát csak erősen légritka közegben, vákuumban lehetséges.
A mozgó levegőnek és víznek azért van hangja, mert az atomok egymáshoz képest elmozdulnak benne. Ilyen a szél sustorgása, süvítése vagy dübörgése, a folyóvíz csobogása vagy morajlása. Ezen természeti hangok közös jellemzője a turbulencia, a közegben fellépő kaotikus örvénylés. A tiszta és rendezett, irányított áramlás gyakorlatilag zajtalan, mert az atomok egymáshoz képest alig mozognak, minimális a deformációjuk és súrlódásuk. A gyakorlatban azonban a gázokban és folyadékokban mindig fellép turbulens mozgás, ami összekeveri az atomokat, molekulákat és zajt kelt. A turbulencia olyan áramlás, aminek az időfüggése nem megjósolható, mivel az áramlási útvonalak nem ismétlődnek (szabálytalanok).
Ezért nem lehet teljesen zajtalan járművet (hajtómotort, repülőgépet, hajót) készíteni, mert a súrlódási zaj mellett a turbulenciát sem lehet semmiféle áramlási profillal megszűntetni. Még akkor sem, ha transzcendens hullámtérrel taszítjuk el a burkolattól a közeg részecskéit (erőtérpajzzsal). A hangtompító, a hangot ellenfázisú rezgéssel kioltó berendezések sem teszik zajtalanná a mozgást, csupán kvázi kioltják azt, erősen legyengítve a lökéshullámok terjedését a közegben. Ez sosem lehet tökéletes minőségű, de ahhoz elég jó, hogy füllel mit se halljunk vagy csupán enyhe sistergésre korlátozódjon a zaj.
A hangrezgés mindig egy mozgó forrásból indul ki, ami meglöki a közeg részecskéit sugárirányban. Mivel a lökés minden elért részecskére átadódik (részben vagy egészben), gyorsan szétterül egy gömbfelület mentén. Ez azt eredményezi, hogy erőssége a fizikai távolsággal négyzetes arányban gyengülni fog, mígnem elenyészik, pontosabban a közeg háttérzajával egyenlő nagyságúra csökken.
A hangforrás rezgése többnyire kétpont oszcillációt jelent, ami némileg aszimmetrikussá teszi a hanghullám erősségét. A rezgés irányában terjed elsősorban a hang, de a közeg szerkezete miatt oldalirányban folyamatosan szóródik, szétterül. Ha ezt megakadályozzuk, például egy csőben továbbítva a hangot, akkor a lökéshullám ereje jóval tovább megmarad és messzebbre eljut azonos sűrűség esetén, mint nyílt közegben.
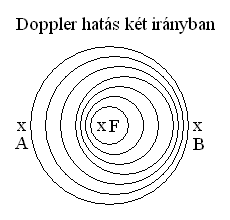
A doppler effektusnak köszönhetően két, egymással ellenkező irányban található megfigyelő számára az ide-oda mozgó forrás zaja egyenlő távolságokban ellentétes fázisban hallható. Amikor A-nak magas F hangja, B-nek alacsony és fordítva. Az emberi fül számára persze mindez a rezgés sebessége miatt gyakorlatilag észrevehetetlen, de attól még tény marad (műszerrel mérhető).
Egyenetlen összetételű közegben a rezgések megtörnek a határfelületeken, szétszóródnak és visszaverődnek vagy elnyelődnek. Nagyjából úgy, ahogy a fénykvantumok viselkednek az anyaggal való találkozáskor. A fény és a hang között viszont fontos különbség, hogy a fénynek saját mozgó forrásrendszere van, míg a hangnak minden általa elért részecske a másodlagos forrása, továbbadója lesz, amíg csak el nem nyelődik a közeg ellenállása (rugalmassága) miatt.
A hangrezgések terjedését a közeget alkotó molekulák, vegyületek térbeli formája szintén befolyásolja. Az atomok többsége a természetben (légkör, víz) kötött állapotban található, tehát nem szabadon mozognak, hanem kisebb csoportokban. A molekulák alakja viszont szinte sosem szabályos gömb alakú, hanem különféle méretű gömbökből összeálló, komplex forma. Ez a súrlódás miatt rontja a gördülékenységet, növeli a viszkozitást, tehát több lesz az ütközés (és tovább tart elcsúszni egymás mellett). Ez némileg növeli a közegellenállást, így hamarább elnyelődik a hullám. Energiája arra fordítódik, hogy elmozgassa egymáson a molekulákat. A molekulákat összetartó másodrendű kötések további energiát vonnak el a hullámtól, így a gyengülése valójában nem a négyzetes szabály szerint következik be, hanem még annál is nagyobb mértékben.
Ha egy atomnak csak az elektronjait rángatjuk, kényszerítjük a normál mozgásától eltérő rezgésre, az többnyire nem kelt hallható hangot. Ezért csendesek a villanyvezetékek és az elektromos gépek többsége, mivel bennük csak vánszorognak az elektronok lökdösődés közben. A hálózati brummnak nevezett jelenséget az elektronok mozgásának mellékhatása (rezonancia) kelti a berendezésekben. Ezt hívjuk lényegében ellenállásnak, mivel a vezetőben vándorló elektronok folyton beleütköznek a maghoz kötött elektronokba és félrelökődnek, turbulens áramlásra kényszerülve az anyagban. Ennek ereje deformálja az atomrácsot, brummogó hangot keltve.
A 3D-s anyagi világban (ahol részecskék vannak) tehát soha nincsen csönd, legfeljebb az atomi lökdösődés háttérzaja túl gyenge az emberi fül számára. De vajon mi történik alacsonyabb vagy magasabb dimenziószámú kiterjedésekben? Feltéve, hogy más dimenziószinteken is vannak stabil elemi részecskék, atomok és molekulák, a közegben terjedő rezgéseknek követniük kell a térben megfigyelhető alapszabályokat. A következő fejezetben ezekkel a valószínűsíthető folyamatokkal foglalkozunk.
3. REZGÉSEK N DIMENZIÓBAN
Általános szabály, hogy minden részecske ütköztetésnek van irányvektora, amerre a lökés tovább adódik. A gyakorlatban ez rengeteg vektort jelent az egymással szomszédos részecskék között, így makro szinten inkább azt mondjuk, a hanghullám skalárisan terjed minden irányban és modulációja longitudinális. A természetben a legtöbb rezgés longitudinális jellegű, a transzverz hullámok igen ritkák, így ez a szabály valószínűleg más dimenziószinteken is érvényes lesz.
A skaláris kiterjedések globális iránya elsősorban a közeg kiterjedésétől függ, amit a beágyazási környezet téridejének dimenziószáma limitál. A 3D-ben a hanghullámok maximum 3D-s gömbként terjedhetnek, de egy vékony fémlemezben, ami kvázi 2D-s, követik az anyag síkszerű kiterjedését.
Az alábbiakban azt vizsgáljuk meg, hogy az egyes dimenziószinteken milyen irányokban terjednek az egy pontból induló hangrezgések és ez milyen következményekkel jár a fizikai tulajdonságaikra nézve.
Az 1D-s száluniverzumban két irányba terjedhet a rezgés. Akár egy, akár két pontnyi vastag a szál, a szakaszatomoknak gyakorlatilag nincs lehetőségük kitérni előle, így csupán a rugalmasságuk gyengítheti a rezgést. Amennyiben a szálat alkotó időpontok teljesen merevek (abszolút rugalmatlanok), a lökéshullám semmilyen távolságon nem enyészik el, vagyis a végtelenségig fog terjedni a rendszerben. Ha a szál egy körvonal, akkor minden rezdülés (elmozdulási információ) a végtelenségig fog benne keringeni, egymásra szuperponálódva. Csak a pontosan ellenfázisú és egyforma nagyságú rezgések képesek egymást kioltani ha szembetalálkoznak. Ha a szál teljes hosszában tömör és rugalmatlan, akkor kvázi végtelen sebességgel átadódik egyik végétől a másikig minden lökés, ami azonnali információ átvitelt tesz lehetővé. Az időszál univerzum persze nem így működik, ott egészen más okokból kerül át a jel a művonal túloldalára, de ezzel majd más írásokban foglalkozunk részletesen.
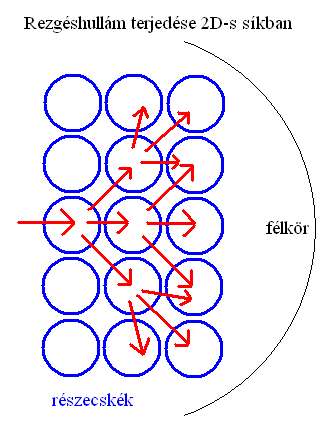
A 2D-s síkuniverzumban körkörösen terjedhet a rezgés. Az egymással szomszédos síkatomoknak egy szál határa mentén van lehetőségük elmozdulni, amikor a lökéshullám eléri őket. Ez 180 fokos kitérést jelent ideális esetben, de a gyakorlatban ennél jóval kevesebb lesz, a sűrűségtől és más paraméterektől függően. A 3D-s térhez képest ezek a körhullámok 1D-s felülettel rendelkeznek, tehát a távolsággal egyenes arányban fog gyengülni az erejük. Feltéve, hogy a síkatomok sűrűsége, súrlódása, tömegtehetetlensége és rugalmassága azonos a térbeli atomokéval (valószínűleg nem azonos, más okokból). Így a síkemberek akár több kilométeres távolságból is képesek beszélgetni egymással, vagyis a közeg sokkal hangosabb, zajosabb, mint a térbeli.
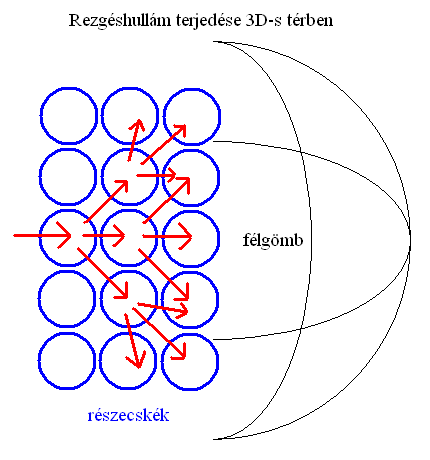
A 3D-s téri univerzumban gömbszerűen terjedhet a rezgés. Az egymással szomszédos térbeli atomoknak egy gömbfelszín mentén van lehetőségük elmozdulni, amikor a lökéshullám eléri őket. Ez 180x180 fokos (félgömbi) kitérést jelent ideális esetben, de a gyakorlatban ennél jóval kevesebb lesz, a sűrűségtől és más paraméterektől függően. A 2D-s felület miatt a távolsággal négyzetes arányban gyengül a gömbhullámok ereje (nagyjából).
A 4D-s túltéri univerzumban hipergömbszerűen terjedhet a rezgés. Az egymással szomszédos túltérbeli atomoknak egy hipergömbtérfogat mentén van lehetőségük elmozdulni, amikor a lökéshullám eléri őket. Ez 180x180x180 fokos (félhipergömbi) kitérést jelent ideális esetben. A 3D-s térfogat miatt a távolsággal köbös arányban gyengül a hipergömbhullámok ereje (nagyjából). Ebből az következik, hogy jobban elnyelődik és elgyengül minden hang a 4D-ben, mint a 3D-ben. Talán csak centiméterekre vagy milliméterekre terjednek a hangrezgések, vagyis az ember a saját hangját sem fogja hallani, bárhogy kiabáljon. Az 5D-ben pedig még totálisabb, süket csend van ezek szerint.
A 4D-ben tehát dimenziószerkezeti okokból nem terjedhetnek messzire a hangok (anyagi lökéshullámok). Feltéve, hogy az elemi részecskék és atomok térbeli szerkezete és az őket összekötő kölcsönhatások nagyjából olyanok, mint a 3D-s térben. Ezzel a kérdéssel majd külön szakmunkákban foglalkozunk a 4D-s anyagtechnológiai kutatásaink keretében.
A részecskék, tárgyak mozgásának gravitációs dopplerje ugyanúgy észlelhető a lélek számára, mint a hangrezgés a fül számára. Ennek terjedéséhez azonban nem kell közeg, így vákuumban is megmarad, és nem gyengül a távolsággal arányosan, csupán fokozatosan belevész a környezet gravitációs háttérzajába a szemlélő számára. A lélek ezeket a gravitációs hullámkép torzulásokat képes hangszerű érzetként felfogni, annak látni.
A 4D-s túltérben (asztráltérben) végzett eddigi parafelderítéseink egyértelműen azt mutatják, hogy ott gyakorlatilag nincsenek hangok. A 4D-ben süket csönd van, nem csak a levegőben, de a vízben is. Az emberi füllel legalábbis nem lehet hallani semmit. Az más kérdés, hogy a lélekkel való közvetlen látás lehetővé teszi a hangok érzékelését, amit a lélek operációs rendszere képes akusztikus jellé alakítani, hogy hanghatásként realizálódjon a feltudatban. Ennek köszönhető, hogy a 4D-s világokban is van zene és ének, amit ráadásul nem korlátoz le a fül érzékenysége, tehát messze szélesebb frekvenciatartományban élvezhető, mint a 3D-s Földön.
Amit a későbbi kísérletek során feltétlenül ki kell majd próbálni, az az lesz, hogy vajon az erős hanghatások megrezegtetik-e az ember bőrét (dübörgő hangfal) és ha igen, akkor milyen messziről? Az n dimenziós látás terén szerzett eddigi tapasztalatainkkal és egyéb furcsaságokkal még sokat foglalkozunk majd, főleg lélektani és emanikai írásainkban.
Készült: 2004.12.27. - 2006.05.19.
Következő írás
Vissza a tartalomhoz