Ebben az írásunkban összefoglaltuk mindazon régi elméleteinket, melyekkel megpróbáltuk egyesíteni az első időtopológiai modelljeinket az időgeometriai elképzelésekkel. Az akkori kísérletek ugyan nem hoztak teljes sikert, mivel hiányzott az n dimenziós matematika számos eleme, viszont több érdekes és fontos adalékkal szolgáltak a későbbi kutatásokhoz. A különféle modellek egyesítéséhez a szalagológiai kutatások adtak nagy lendületet, mert a szalagok tulajdonságainak könnyű mérhetősége biztos támpontot nyújtott a megoldások keresésében.
Technikai okokból sajnos az időhurok rendszerek számítógépes modellezése a mai napig gyerekcipőben jár, nem bírván túljutni bizonyos alapvető problémákon. Viszont a szalagológia szabályai bárki számára elérhető és egyértelmű leképzésekre adnak lehetőséget. Általuk sikerült először biztos és bizonyítható tudást szereznünk a teremtés működésének legbelső, ezoterikus titkairól, a legszentebb tudásról. Ami az okforrások és másolataik szerkezetével, valamint az időhullámok fizikai jellemzőivel kapcsolatos.
1. SZALAGOK ÉS IDŐHULLÁMOK
A kétszer egymás után szimmetrikusan felvágott Möbius-szalagból két egymásba fonódó Tetrás-szalag lesz, amik síkba kilapítva két összefont négyzetet adnak. Ezt egy nyolcágú csillag formájába lehet kifeszíteni. (1. ábra) A Tetrás-szalagok nyolcas alakzatba való eligazítása pedig egy térbeli Bindut, négyszirmú virágot (fénymagot) alkot. (2. ábra)
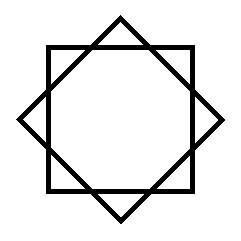
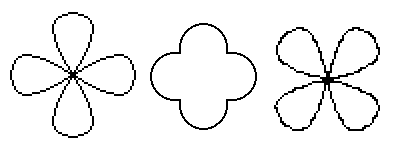

Ha tovább hasítjuk a szalagokat, s közben eltekintünk attól a fizikai következménytől, hogy a szalagok egyre vékonyabbak lesznek, akkor az n. lépés után egy nagy gubancot kapunk. Ez sok egymásba font négyzetből áll, amik síkba kilapítva egy tömör körlapot adnak. Ha a szalagokat széthúzzuk, akkor egy síkgyűrű lesz az eredmény, a nyolcágú csillag n ágú változata. (3. ábra) A körlap és a gyűrű nem tekinthetők valódi 2D-s kiterjedésnek, mert a kölcsönös átfedések miatt a vastagságuk több helyen meghaladja a három szalagnyit (lásd: a hárompont-tételt), tehát térbeliek lesznek.
A matematikában a klasszikus Lissajous-görbék (másnéven Bowditch-görbék) nagyon hasonlítanak ezekre, amik szerkezete a merőleges tengelyű hullámmozgások interefrenciájából adódik. Eme görbék harmonikus rezgések összegzésekor keletkeznek, eltérő vektorok estén.
Mindkét gubancban a Tetrás-szalagok egy időhullámrétegnek felelnek meg időfizikailag, amik elhagyták a forrásukat. Ha a térbeliségüknek megfelelően kiemeljük őket (gondolatban) a 3D-be, akkor egy kvázi tömör gömböt és egy kvázi lyukas gömböt kapunk. A tömör gömb az álló forrás VÍZ típusú hullámterének felel meg. Belső időszerkezete kvázi folytonos, mégis kvantálható az egyes szalagok (hullámrétegek) segítségével.
Valódi tömör gömböt akkor kapunk, ha aszimmetrikus felhasításokkal hozzuk létre azt a Möbius-szalagból. Ekkor ugyanis a gubanc közepén mindig megmarad egy Möbius-szalag (a jelenforrás), ami biztosítja a Tetrás-szalagok közti kapcsolatot (az idő folytonosságát). Ez fizikailag mozgatható a gubancon belül, az egymásba láncolt szalagok rugalmassága (pontosabban deformálhatósága) miatt. Elvileg nem csak tardionként, hanem tachionként is, ha a forrást kihúzzuk a gömbből, mert ekkor minden Tetrás-szalag nyúlni fog utána, mivel rá vannak fűzve.
Papírból ezt a műveletet a gyakorlatban nem lehet megcsinálni szakadás nélkül, esetleg gumicsíkokkal modellezhetnénk némi erőfeszítéssel a szemléletesség kedvéért. De elméletben könnyen belátható a térbeli szerkezet ismeretében, hogy az eredmény mi lesz. Egy tömör gömbből képzett tömör csepp (kúp) alak a térben.
A másik változat, a lyukas gömb a forrását vesztett időhullámokat reprezentálja. Ha a jelenpont eltávozik a saját időgömbjéből (tachionként vagy térugrással), akkor a visszamaradó meddőhullámok nyomában egy térszünet fog terjedni kifelé a továbbiakban. Ha a jelenpont valamiért megszűnik létezni, akkor a visszamaradó árvahullámok nyomában egy létszünet fog terjedni kifelé a végtelenségig. Ezt a Möbius-szalag szimmetrikus felhasításával lehet modellezni, ami megszűnteti a Möbius-szalagot, csak Tetrás-szalagokat hagyva meg a gubancban.
Ha a gubancunk szerkezetét az univerzum térbuborékára vonatkoztatjuk, az ősi (hindu) szent iratokban olvasható teremtési fázisok működését kapjuk teljes pontossággal. Az első lépésben az időforrás (térszerán) kiárasztja múltját, ami felfúvódik és létrehozza a világtojást (Brahma teremt). Ezt követi a létrehozott rendszer fenntartása, az időtöltés (tömör gömb), amikor a rendszer gyarapodik és bonyolódik a kezelhetőség határáig (Visnu megtart). A harmadik lépésben valamiért szünetelni kezd a kiáradás, vagy mert megszűnt a forrás (az Isten halála miatt) vagy mert térosztással térszünetet tart a Mindenható (Siva pusztít).
A térszünet és a létszünet keltése nem "létrehozás", mert ezek a létezés hiányát okozzák, elpusztítva az útjukba kerülő teremtményeket (az istenségek és démonok kivételével). Ekkor a forrásukat vesztett időhullámok szétrohanva mintegy kilapulnak a buborék falán (a Nagy Vonzón), s belül egyre nől, terjed a térszünet gömbje. Ez a megsemmisülési hullámfront bentről kifelé haladva fénysebességgel lebontja az univerzumot. Krisna, a legfelsőbb Isten ezért felébred álmából (a teremtésből), s a lét átmenetileg a megnyilvánulatlanság állapotába kerül. Ekkor minden információt hordozó időhullám mintegy fellapult az időgömb falára (lyukas gömb). A tudás nem veszett el, csak összegyűlt a világ peremén (az óperenciás tengeren túl, de az üveghegyen még innen) és ott is marad örökké, tovább terjedve a végtelenbe.
A térszünet során a világbuborék falát alkotó neutronpáncél, a Nagy Vonzó nem bomlik le, mert azt a megmaradó hiperterek (egy vagy két térhatos) továbbra is fenntartják. Ott ugyanúgy tömörül a létezés, a végletekig (annihilációs határértékig) összesűrűsödve, ahogy a lyukas gubanc szalagjai a gyűrűben.
2. SZALAGOKKAL KAPCSOLATOS SZÁMÍTÁSOK
Vizsgáljuk meg a Möbius-szalag aszimmetrikus felhasításakor keletkező, síkba kilapított Tetrás-szalagokat alaposabban. A belőlük kapott lyukas gömb falának vastagsága, ha az egyszerűség kedvéért négyzetekbe lapítjuk ki az összes szalagot, a beleírható kör és a köré írható kör sugarának különbsége lesz. Feltéve, hogy eltekintünk a Tetrás-szalagok térbeli vastagságától, s egyszerű négyzeteknek tekintjük őket (némi egyszerűsítéssel). (4. ábra)
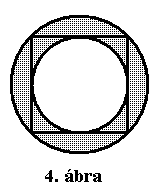
b = a négyzet oldala,
r = a négyzetbe írt kör sugara,
R = a négyzet köré írt kör sugara,
k = a négyzetbe írt kör kerülete,
K = a négyzet köré írt kör kerülete,
t = a négyzetbe írt kör területe,
T = a négyzet köré írt kör területe,
ak = a négyzetből képzett kockába írt gömb felszíne,
Ak = a négyzetből képzett kocka köré írt gömb felszíne,
vk = a négyzetből képzett kockába írt gömb térfogata,
Vk = a négyzetből képzett kocka köré írt gömb térfogata,
ro = a négyzetből képzett oktaéderbe írt gömb sugara.
Ro = a négyzetből képzett oktaéder köré írt gömb sugara.
ko = a négyzetből képzett oktaéderbe írt gömb kerülete.
Ko = a négyzetből képzett oktaéder köré írt gömb kerülete.
ao = a négyzetből képzett oktaéderbe írt gömb felszíne,
Ao = a négyzetből képzett oktaéder köré írt gömb felszíne,
vo = a négyzetből képzett oktaéderbe írt gömb térfogata,
Vo = a négyzetből képzett oktaéder köré írt gömb térfogata.
Ha b = 1, akkor:
r = 0,5
R = (gyök2)/2
k = Pi
K = (gyök2)*Pi
t = 0,25*Pi
T = 0,5*Pi
ak = Pi
Ak = 2*Pi
vk = (4*Pi/3)*0,5^3 = 0,523598775
Vk = (4*Pi/3)*((gyök2)/2)^3 = 1,480960979
ro = (gyök6)/6 = 0,40824829
Ro = (gyök2)/2
ko = ((gyök6)*Pi)/3 = 2,56509966
Ko = (gyök2)*Pi
ao = 4*Pi*(gyök6/6)^2 = 4/6*Pi
Ao = 2*Pi
vo = (4*Pi/3)*((gyök6)/6)^3 = 0,287674728
Vo = (4*Pi/3)*((gyök2)/2)^3 = 1,480960979
Mivel T = t*2, ezért a gyűrű területe egyenlő a körbe zárt belső lyuk területével. Ha a gyűrűt kihúzzuk térbeli lyukas gömbbé, akkor a fal térfogata nagyobb a gömbbe zárt belső lyukénál. A lyuk térfogata 35,3553%-a a teljes gömbnek.
3. SZALAGOK ARÁNYOSSÁGA
Ha a Möbius-szalag hosszát egységnyinek tekintjük, akkor a felhasítása során keletkező Tetrás-szalag dupla hosszúságú lesz. Ha a két szalagot 1D-s szakasszá redukáljuk (időszál), akkor a hosszuk feleződik a félbehajtás miatt. A Möbius-szalag egyoldalú felületét kétszer kell körbejárni ahhoz, hogy egyszer visszaérjünk a kiindulási pontba, míg a két oldalú Tetrás-szalagot csak egyszer. Ugyanakkor a Möbius-szalagon egy 180 fokos csavarodás van, a Tetrás-szalagon pedig négy. Megfigyelhető, hogy a megnyilvánulási folyamat során a következő arányosságok jelentkeznek a szalagok egyes paramétereiben: 1:2:4. Ez a fajta duplázódás érdekes számtani összefüggést mutat a tér fizikai szerkezetének modelljével, ahol a 0D-s pontból 1D-s szál, majd 2D-s sík, végül 4D-s spirálgömb lesz a tengelypáros terek esetén (a 3D kimarad).
Ha az értékeket négyzetre emeljük, akkor: 1:4:16. Azt pedig tudjuk, hogy az univerzumunk 1séges rendszere 4D-s téresszenciákból áll, amikből a triásztéridőben 16 db van. Erre már rá lehet mondani, hogy "számmisztikai összefüggés", mivel a mélyebb okokat illetően egyelőre csak találgatni tudunk.
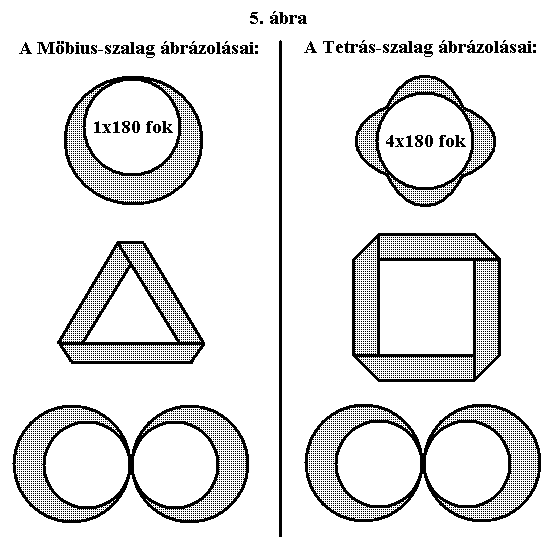
Most tekintsünk el a szalagok szalagszerűségétől, és tekintsük őket úgy, mint görbéket, egyszerű vonalakat. Ha lerajzoljuk a Möbius-szalagot és a Tetrás-szalagot, nyomban rájövünk, hogy ezt többféleképpen is megtehetjük geometriailag. A Möbius-szalag ábrázolható körként, háromszögként és fekvő nyolcasként (lemniszkátaként, ami lényegében két érintkező kör). A Tetrás-szalag ábrázolható körként, négyzetként és fekvő nyolcasként (lemniszkáta). (5. ábra) Ezek a legegyszerűbb geometriai síkidomok, amikből minden bonyolultabb struktúra felépíthető. Az egyenlő szárú háromszög isteni szimbólum, míg a négyzettel a világ négy sarkát (égtáját) szokták jelölni. A következő fejezetben a háromszöggel kapcsolatos ezoterikus ismeretek viszonylag kevéssé ismert részét foglaltuk össze, amik az időforrással való kapcsolatára utalnak évezredek óta.
4. A DELTA FORRÁSPONT
A görög ABC negyedik betűje a D, mint Delta. Lerajzolva a nagy betűs változata egy háromszög lesz, a kis betűje pedig egy nyolcasra (lemniszkátára) hasonlító hurkos köröcske. (6. ábra) A nyolcas befejezetlensége valószínűleg utalás arra, hogy ez még készül. Mivel mozog, keletkezik, áramlik benne az idő.
A latin ABC-ben a D egy félkör. Ha a megnyilvánulást (múltszférát) gömbnek tekintjük, akkor az ábrázolása egy kör lesz. A félkör tehát az ezt megelőző állapotra, a kör készülésére tett szemléletes utalás. Nem egyszerűen a megnyilvánulatlan, ami egy pont lenne, hanem a forrásban fortyogó idő mozgásának ábrázolása, tulajdonképpen az átmeneti állapot a vanásból a létbe. Mivel a létezéshez két forráspont kell, amik D betűi összerakva már egy kört (egészet) alkotnak.

A delta szó jelentése a magyarban folyótorkolat, ahol a folyó háromszög alakban, több szálra szakadva szétágazik, s úgy fut bele a tengerbe. A másik folyótorkolat a szétágazás nélküli tölcsértorkolat, ami szintén háromszög formájú (síkban), mégis a kúp alakú tölcsér (térbeli forma) nevét viseli.
A delta a vasúti technikában a sínháromszöget jelenti, a matematikában a függvény differenciáját jelölik vele, a szerves vegyületek kémiájában pedig a kettős kötés helyzetét. Hogy egészen egyértelmű legyen, milyen ezoterikus jelentése van a szónak, a héberben a delta, mint daleth szó jelentése: kapu! Ez az idő kapuja, forrása. A deltás szó jelentése emellett még a magyarban szép, szabályos, erős, egészséges.
A XX. században az MTV műsorán évtizedekig ment a Delta című tudományos ismeretterjesztő műsor, amiben az emberiség aktuális (jelenbeli) tudását mutatták be. A műsor emblémája természetesen a háromszög volt.
A kereszténységben a háromszög Szentháromság néven közismert, ami az Isten hármas szerkezetének fölöttébb homályos és máig csak kevés beavatott által igazán értett ábrázolása. Főként azért zavarosak a vele kapcsolatos vallási fogalmak, mivel többféle filozófiai, matematikai és ezoterikus magyarázat (leképzés) is létezik rá nézve, de elsődlegesen valóban az Isten, mint okforrás szerkezetével kapcsolatos ábráról van szó.
A deltából képzett további szavak logikailag szintén az eredeti jelentésre utalnak: delta-elektron, deltafém, deltaizom, deltakapcsolás, deltamoduláció, delta-részecske, delta-sugárzás, deltaszárny, deltavágány, deltoid, deltás izmú. Mindezek mellett van még Delta nevű hordozórakéta, légitársaság, változócsillag típus és kihalt ősállat (deltatheridium) is!
A figyelmes Olvasó talán észrevette, hogy a deltával kapcsolatos ismeretek felsorolásakor gyakorlatilag a teremtés összes fontos alkotóját meg kellett neveznünk. Ezek zárójelben a következők: delta-elektron (elektron), delta-fém (proton), delta-részecske (neutron), delta-izom (az élőlények húsa), delta-kapcsolás (kölcsönhatás, kapcsolat), delta-vágány (időszál és elágazásai), delta-moduláció (információ), delta-sugárzás (az időhullám kiáradása és az energia kvantumos formái), delta-torkolat és deltaszárny (forma, téridőbeli mozgás és deformáció), deltoid (sárkányidom forma), függvény differencia (sokszínűség és változatosság), deltás kinézetű személy (lélek).
5. SZALAG ÉS TÉRFORRÁS
A Möbius-szalagot (ami 180 fokos) felhasítva 720 fokos Tetrás-szalagot kapunk, ami megfelel a tardion folyóvíz szerkezetének. A Pentás-szalagot (ami 5x180 fokos, tehát n=5) felhasítva 2160 fokos öthurkos szalagot kapunk, ami pedig megfelel a téridő spirálgömbi szerkezetének. A két időrendszer (egy forrásos és öt forrásos) eltérő csavarodási jellemzőjű, bár mindkettő kétoldalú a megnyilvánulásában. Ha az öthurkos szalag csavarodását úgy osztjuk fel, hogy 12x180 fok (azaz 12-szer félfordulat), akkor ez 3 db Tetrás-szalaggal (4x180 fok) egyenértékű csavarodásnak felel meg. Csakhogy a térszeránból 5+1 db spirálgömb árad kifelé egymásba ágyazva, amik így egyenként nem 720, hanem 360 fokosak lesznek. Itt nem teszünk különbséget a téresszenciák és a nemtér-nemidő réteg térszünete között, amit szintén egy önálló spirálgömbnek tekintünk az egyszerűség kedvéért.
Felmerül tehát a kérdés, hogy miért fele annyi csavarodású a téridő forrásonként (2x180 fok), mint a sima VÍZ (4x180 fok)? Talán mert az időhurokban a forráspontok sosem írnak le egy teljes kört, hanem csak egy ív mentén rohanak végig újra és újra, minden ciklusban elölről kezdve az életüket. Így a hullámterük sem lesz teljesen zárt, ráadásul önmagából félig kifordul a tachionikus sebességük miatt.
A térszorzással készített diásztéri és triásztéri forrásrendszer nem modellezhető megfelelően szalagokkal, mivel ilyenkor nem nő arányosan az időforrások száma, csupán a forráshelyeké a hurok másodlagos rotációja miatt. A három térhatos ráadásul időben nem egyszerre, hanem felváltva (időosztásos módban) létezik, így egyszerre mindig csak az egyik van jelen az idősemmiben.
Készült: 2003.01.03. - 2004.01.03.
Következő írás
Vissza a tartalomhoz