1. A TÁVOLSÁG MÉRÉSÉNEK ELVI ALAPJAI
A 3D-s térben a tárgyak közti távolság mérése sok paramétertől függ, attól függően, hogy mit tekintünk távolságnak. A távolság meghatározását befolyásolja a tárgyak alakja (formája és deformációja) és mozgása (helyváltoztatása és helyzetváltoztatása) egymáshoz képest. Két szabálytalan tárgynak alapvetően négyféle fizikai távolsága definiálható, amennyiben nem mozognak egymáshoz képest.
Az első a legkisebb távolság a két tárgy egymáshoz legközelebbi két pontja között. Általában erre vagyunk kíváncsiak, amikor távolságról beszélünk. A második ennek az ellenkezője, a legnagyobb távolság a két tárgy legtávolabbi pontjai között, amik lehetnek láthatóak vagy takarásban lévők fizikailag. Erre többnyire nem vagyunk kíváncsiak.
A harmadik a középponti távolság, ami a két tárgy köré írható gömbök origói között mérhető. A tömegek (égitestek) kölcsönhatása esetén többnyire erre vagyunk kíváncsiak, bár szabálytalan (nem gömbszerű) objektumok esetén ez nem mindig esik egybe a tényleges tömegközépponttal. A negyedik pedig a tárgyak tömegközéppontjai közti távolság, ami alapján a mozgásukra vonatkozó információk kiszámíthatók.
A gyakorlatban a távolságot a két végpont közti 1D-s egyenes hossza határozza meg a téridőben. A téren kívül (a 0D-s nemtér-nemidőben) nem értelmezhetők a távolságok, az őskáosz fizikai tulajdonságai miatt, ezért ott a mozgás sem definiálható ellentmondásmentesen. Azt tudjuk, hogy a párhuzamos téresszenciák valójában csak 1D-sek (a kiáradásuk okán), de a hullámterük csavarodási jellemzői miatt több dimenziósnak látszanak (4D-snek). Ezekben a fizikai terekben már van metrika, méghozzá idő alapú. A térbeli távolságot ugyanis időbeli mozgással, tartamkülönbséggel, a változás információjának átfutási késedelmével mérjük. Két különböző időpont a térben ezért mindig véges távolságra van egymástól, míg a nemtér-nemidőben nulla távolságra. Ami nulla távolságra van valamitől, az nem különíthető el tőle, épp ezért egy időpontot alkot. Ezért ellentmondásos minden jelenség az őskáoszban.
2. TÁVMÉRÉS SZABAD SZEMMEL
Ha tudom, mekkora egy bolygó átmérője, az űrből nézve a látszólagos átmérőjéből (hány foknyinak látszik) ki tudom számítani a távolságát tőlem, az elmozdulásából pedig a saját relatív sebességem a bolygóhoz képest. Ennek a módszernek az az előnye, hogy egyszerű, passzív optikai műszerekkel, sőt némi gyakorlat után szabad szemmel, becslés alapján is meg lehet mérni a távolságot (csak a bolygók átmérőit kell bemagolni).
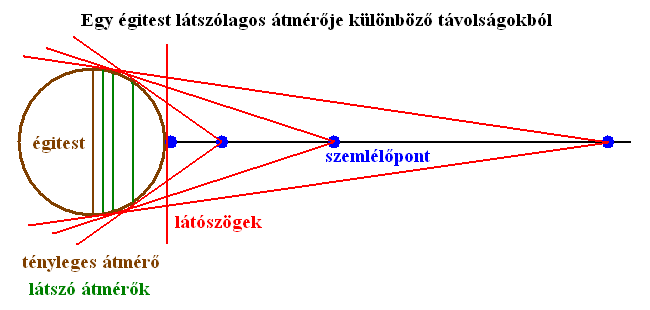
Minél messzebb van az űrhajó a bolygótól, az alfa látószög annál kisebb, de nagyobb nullánál minden véges távolságon. (1. ábra) Az emberi szem felbontóképességének korláta miatt egy adott távolságon túl minden bolygó pontnak látszik, ezért az alfa kvázi nulla lesz. Nulla távolságból pedig, az égitest felszínéről nézve a bolygó síkfelületnek látszik, tehát az alfa 180 fokos lesz. Ebből következik, hogy a látszólagos átmérő 180 fok esetén végtelennek adódik, 180 és 0 fok között pedig mindig kisebb lesz a valódi átmérőnél. Egy gömbszerű égitestet tehát a levegőből vagy az űrből mindig kisebbnek látunk (egy pontból szemlélve), mint amekkora valójában. Csak 0 fokos alfaszög esetén lesz a látszólagos átmérő egyenlő a valódi átmérővel.
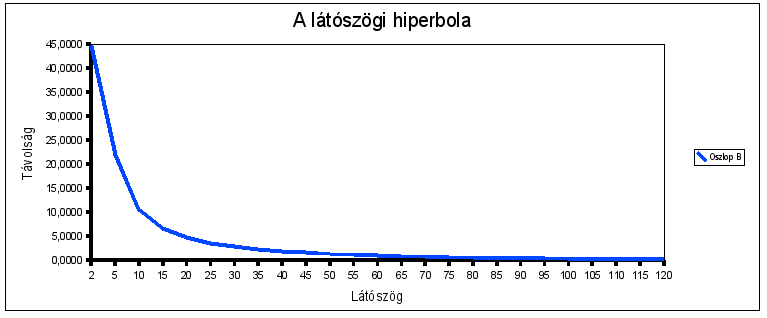
A látószög változása a távolság függvényében exponenciális, vagyis egy hiperbola görbe mentén mozog. Az alábbi táblázatban látható, hogy egy egységnyi sugarú égitest különböző távolságokból hány fokátmérőjűnek látszik. (2. ábra)
3. KOZMIKUS TÁVÉRZÉKELÉS
A világűrben hatalmasak a távolságok, gyakorlatilag nem emberi léptékűek. Ezt csak az tudja igazán felfogni, aki tapasztalta már, de ilyen ember nem sok van jelenleg a Földön. Az emberek korlátolt elképzeléseit jól tükrözi, hogy a fantasztikus filmekben a világűrbeli objektumokat és mozgásukat szinte mindig pontatlanul ábrázolják, az emberi szem léptékének és felfogóképességének megfelelően. Akinek nincs összehasonlítási alapja, az észre sem veszi, hogy az űrhajók mozgása teljesen irreális a távoli bolygókhoz és pláne a csillagokhoz képest, mintha az univerzum egy pár kilométeres kis szűk helyecske lenne a jármű körül. Mindennek persze elsődlegesen a látványosság a célja, mert a gyakorlatban szabad szemmel lehangolóan mozdulatlanok lennének a csillagok még százszoros fénysebességű száguldás esetén is. Nem beszélve arról, hogy az űrhajók sem száz méterekről lövöldöznek egymásra egy űrcsatában, hanem kilométerek ezreiről, ahonnan a másik jármű még pontnak sem látszik távcső nélkül. Ezzel a témával korábban részletesen foglalkoztunk a Katonai űrhajók felépítése és működése című írásunkban.
A kozmoszban a tájékozódás első és legfontosabb akadálya és nehézsége maga a távolság, az égitestek közti irdatlan üresség, amit még műszerekkel is roppant nehéz felderíteni. Ennek köszönhető, hogy még az észlelhető objektumok elsöprő többsége is csak pontszerű látvány egy határon túl, így a pozícióján és mozgásán (parallaxisán) kívül nem sok mindent lehet megtudni róla alaposabb vizsgálatok és hosszadalmas mérések nélkül. A világűrben mozgó kisebb-nagyobb tárgyak észlelése, felderítése egy űrhajón ezért állandó elfoglaltságot jelent a műszerek és a személyzet számára. A témával korábban részletesen foglalkoztunk az Űrstratégiai elgondolások című írásunkban.
A környezet felderítése a következő módokon történhet.:
1. Az égbolt fényképezése különböző spektrumokban, elsősorban az infravörös, látható, ultraibolya, röntgen és gamma tartományokban. A kapott felvételek összehasonlításával lehet parallaxist mérni a közeli objektumokra, összevetni a csillagászati térképekkel a navigációhoz és spektrál analízissel megállapítani az objektumok összetételét.
2. A radarozás, mint aktív felderítési technika a rádióhullámok lassú terjedési sebessége miatt csak kis távolságokban lehet eredményes. Egyrészt a visszaverődési késedelem miatt, másrészt mert a jelek erőssége a távolsággal négyzetes arányban gyengül. A kis méretű és a hullámokat rosszul visszaverő testek pedig nem észlelhetők vele nagyobb (pár ezer kilométeres) távolságból. Földi viszonyok (méretek) között a radarozás nagyon eredményes lehet, de kozmikus távolságokon reménytelenül használhatatlan.
3. A gravitációs hullámok érzékelése, mint passzív felderítési technika kicsivel hatékonyabb, mint a radarozás, mivel a gravitációs távcső nem bocsát ki hullámokat, csak veszi őket. Így a jelek futási késedelme a radarhoz képest felére csökken és az a gond sem lép fel, hogy egyes objektumok rosszul verik vissza a radarhullámokat. Minden ami anyagból van gravitációs hullámokat bocsát ki magából, folyamatosan és leárnyékolhatatlanul, ezért gravizorral észlelhető. A módszer hátránya, hogy a hullámok áthatolóképessége miatt egy adott irányból minden objektum egyszerre látszik, egészen az univerzum határáig. Emiatt a minket érdeklő távolságon belüli tárgyak lokalizálása csak több műszeres méréssel, parallaxis vizsgálattal szűrhető ki. A témával korábban részletesen foglalkoztunk Az emanika alapjai című írásunkban.
A földönkívüli űrhajók (ICŰ-k) éppen emiatt visznek magukkal állandóan kísérő szondákat, amik az anyahajó körül cirkálnak egy pár száz méter sugarú gömbben és sok egyéb feladat mellett a gravizorjaikkal felderítést is végeznek.
4. Az űrfelderítés leghatékonyabb módja az, ha közelebb megyünk a vizsgálni kívánt objektumokhoz, hogy a műszereink hatósugarán belülre kerüljenek. Mivel egy űrhajó nem ugrálhat állandóan össze-vissza, hogy minden tárgyat megvizsgáljon maga körül az űrben, célszerű helyette járőrszondákat kiküldeni. Apró felderítő robotokat, amik elvégzik a munkát. Ezen a módon a hajó érzékelése mintegy kitolható, megsokszorozható egy ésszerű határon belül, ami főként harci helyzetben előnyös.
5. A saját kozmitórium (űrfelségtér) állandó felderítésére viszont célszerű kiépített bójahálózatot üzemeltetni, ami megbízhatóbb, mint rendszeres időközönként körbejárni a teret robotszondákkal. Mivel az állandó megfigyelőbóják üzemeltetése költségesebb, ezért csak kisebb tartományok (bolygók környéke) felügyeletére alkalmas. A fény és a gravitációs hullámok terjedésének lassúsága miatt a bóják távolságát 1-2 fénymásodpercben célszerű maximalizálni, hogy relatíve valós idejű adatokat szolgáltassanak a feldolgozó központnak időszálas kapcsolaton keresztül. Mindezek miatt egy kisebb bolygórendszert még le lehet fedni bójákkal, a mélyűrt viszont nem, pontosan a méretei miatt. A sűrűn használt hajózási útvonalak mentén ettől függetlenül érdemes bójaláncot telepíteni, ami segíti a térugrásokat és azonnal tájékoztat a zónán átvonuló objektumokról.
Készült: 2004.10.30. - 2005.10.17.
Következő írás
Vissza a tartalomhoz