A MANDU ÁTMÉRŐJE


1. A JELENPONT MÉRETE

Az elmúlt húsz évben az időfizikai modellek nagyon sokat változtak, de egy dolog sosem volt kérdéses. Az, hogy az idő forrása, a jelenpont nulla méretű. Ez sok szempontból kényelmes meghatározásnak bizonyult, de főként praktikusnak. A lehető legkisebb elemből felépíteni a teremtést logikus kiindulópont, ahogy a görög filozófusok is tették, csak ők Atomnak hívták azt, amit mi Mandu néven emlegetünk. Bár rengeteg publikáció foglalkozott már a Ponttal, mégis sokáig úgy éreztem, hogy maradtak tisztázásra váró részletek vele – a Létezővel – kapcsolatban. Ezeket mostanra sikerült összefoglalnom, s ebben a cikkben vitára bocsátom a Pont méretével kapcsolatos fejtegetéseimet, valamint ennek teremtésfilozófiai következményeit.
Ami létezik, annak formája, szerkezete van. Egy Pont önmagában nem létezik, csak van, tehát nem szükséges, hogy formája, szerkezete legyen. Ennélfogva pusztán elméleti minden olyan leírás, ami a megnyilvánulatlan tulajdonságaival foglalkozik. Két egymás számára létező Pont, amik együtt Bindut alkotnak, már formával, szerkezettel bír (topológiai modellje két egyoldalú tórusz), amit az elmúlt években sikerült részletesen feltárni (had ne soroljam a publikációkat). A Létező két Pontja együtt egy végtelenségig nyúló időszálat, vízvonalat alkot, ami egy harmadik szemlélő számára egy kétfelé nyúló időszál lesz, mindkét végén egy-egy Bindunak látszó Manduval (1. ábra). A kölcsönhatást az időhullám rétegek biztosítják, amik egységnyi sebességgel terjednek minden létező irányban (skalárisan) a végtelenségig. Ezen folytonos időközegnek a források forgása miatt van egy saját frekvenciája, amelynek okán a belseje kvantálható. Ezt nevezzük az idő szerkezetének. Az időtér szerkezete a doppler hatás miatt torzul, a forrás helyváltoztató mozgásának megfelelően.


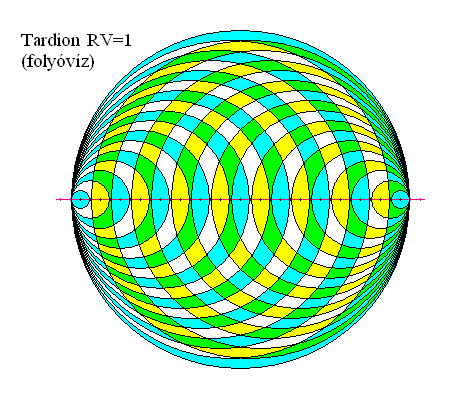
Jelenlegi ismereteim szerint minden okforrás forgásának tengelyiránya és tengely körüli forgási sebessége egyedi lehet az őskáoszban. Valószínűleg a tíz okforrásból öt balos, öt jobbos forgású (lásd: a görög mitológiát), és biztos, hogy mindkét fajtából legalább egy van a minden létezőben. Azt tehát kizárhatjuk, hogy az ismert okforrások forgásiránya csak egyféle lehet. Ha viszont minden okforrás egyedi, akkor a hullámterüknek is egyedinek kell lennie, ami alapján felismerhetők. Az időhullám rétegeik hullámhossza (álló, illetve egyenletesen mozgó forrás esetén) egyedül a forgási sebességtől függhet, más paramétertől nem, ami a forrás mozgási sebességét és irányát ismerve a szemlélőhöz képest, a fix terjedési sebesség segítségével könnyen kiszámolható (megfelelő mérési technika birtokában).


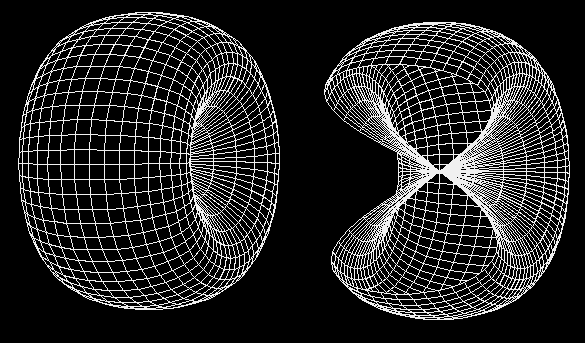
Felmerül a kérdés: van-e kapcsolat a hullámhossz és a Mandu átmérője között? A Mandu átmérője természetesen azonos a Binduéval, amit látunk, mint létezőt, ezért a továbbiakban a jelenpontra csak Manduként fogok utalni (2. ábra). Ha a Pont mérete valóban nulla, akkor ennek a kérdésnek nincs értelme. Elképzelhető azonban olyan modell is, amiben a Pont mérete nem nulla, hanem egy nagyon kicsiny érték. Ahogyan az időhullámok terjedési sebessége sem nulla vagy végtelen, úgy a forrásuk mérete sem lehet nulla vagy végtelen ezen logika szerint, tehát hipotézisünkben tekintsük ezt is egységnyinek. Ez esetben a következő felismerésekre juthatunk.:


Ha a Mandu fél fordulata eredményez egy időhullám réteget, akkor a rétegvastagság (hullámhossz) a fix kiterjedési sebesség miatt csak a forgási sebességtől függ, ami abszolút (megváltoztathatatlan) és okforrásonként egyedi. A szalagológiai modellek szerint amikor egy Möbius-szalagot felvágunk, a keletkező két oldalú Tetrás-szalag hossza a duplája lesz az eredetinek (3. ábra). Ez geometriailag megfelel annak, hogy a Pontból kiterjed a hullámtér, a szálszerű létezésnek megfelelően először csak két irányba. Vagyis a Möbius-szalag hossza (kerülete) egyenlő lesz a megnyilvánuló időgömbjének sugarával. Ebből következik, hogy a Mandu átmérője egyenlő a saját hullámrétege vastagságával (a hullámhosszal), amiből kiszámolható a felszíni forgási sebessége (a tórusznak).

2. A MODELL KRITIKÁJA ÉS AZ AXIÓMA PROBLÉMA

Ennek a modellnek az előnye, hogy kiküszöböltünk belőle egy újabb irracionális paramétert, a nulla dimenziós Pontot. Elvileg azt a megoldást is választhattuk volna ehelyett, hogy a forgási sebességet vesszük fixnek, amely esetben minden okforrás átmérője egyedi, de akkor felmerül a kérdés, hogy melyik mekkora a többihez képest és miért?
Az eddigi körbejáró okoskodásainkból mindenesetre egy nagyon fontos filozófiai (ontológiai) következtetésre juthatunk. A létezés kezdetét leíró modellnek mindenképpen tartalmaznia kell legalább egy olyan paramétert, ami önkényesnek tűnik és nem adható rá logikus (ellentmondásmentes) magyarázat. Lássuk a főbb (eddig vizsgált) lehetőségeket:

1. A jelenpontok mérete nulla, a forgási sebességük egyforma, az időhullámtér hullámhossza és terjedési sebessége egyforma. Ez volt a legelső és legegyszerűbb modellünk, ami akkor vált kérdésessé, mikor felmerült az eltérő hullámhosszak lehetősége. Az őskáoszban megfigyelhető ősidő szerkezetéből viszont az következik, hogy nem állapítható meg teljes pontossággal az egyes okforrások hullámhossza. Erre akkor nyílna lehetőségünk, ha a Mindenható Isten térszeránja mellett lenne még egy elsőrangú térszerán valahol az idősemmiben, ami egy másik okforrástól származik. A két időhurok hullámterét összehasonlítva ugyanis következtetni lehetne az okforrásaik paramétereire.

2. A jelenpontok mérete egységnyi, a forgási sebességük egyedi, az időhullámtér hullámhossza egyedi, a terjedési sebessége egyforma. Ez egy bonyolultabb modell, ami nem bizonyítható, ráadásul az egyediség túl sok kérdést vet fel. Az Occam borotváját használva így célszerűnek tűnik az elvetése. Abba a kérdésbe most ne menjünk bele, hogy maga az Occam elv helyes és használható módszer-e a létezés legvégső természetének kutatásában.

3. A jelenpontok mérete egységnyi, a forgási sebességük egyforma, az időhullámtér hullámhossza és terjedési sebessége egyforma. Ez az első modell javított változata, ami kiküszöböli a nullával és végtelennel kapcsolatos problémákat, viszont megmarad az egyformasággal kapcsolatos fő kérdés: miért egyformák az okforrások?

4. A jelenpontok mérete mérete egyedi, a forgási sebességük egyforma, az időhullámtér hullámhossza egyedi, a terjedési sebessége egyforma. Ez, és az összes többi, lehetséges paraméter kombináció szintén valószínűtlen, a sok önkényes tulajdonság miatt.
Úgy tűnik tehát, hogy az önkényesség (szubjektivitás) egy alapvető és elidegeníthetetlen tulajdonsága a létezésnek, amit másként megfogalmazva úgy is kifejezhetünk, hogy axióma mentes modellt nem lehet alkotni a létezésre. Minimum egy axiómára feltétlenül szükség van, amit szintén axiómaként kezelve szükségképpen tautológiába futunk. Tehát az a definíció, miszerint axióma, hogy axiómára szükség van a modellezéshez, egy öntartalmazó halmazként magát a Létezőt definiálja, így azonos vele. Ez esetben viszont (tovább hasogatva a szőrszálat) a modellünket eleve azzal kezdjük (és nem kezdhetjük mással), hogy: tegyük fel, hogy van egy Létezőnk. Ebből egy csomó dolog logikusan következik, amik szépen levezethetők, további axiómáktól mentesen. Vagyis törvényszerű, hogy az egy axiómás modell semmiben sem tér el a nulla axiómástól, így a kettőt egynek kell tekintenünk.
Az mindenképpen látszik az eddigiekből, hogy a nullából (a 0D-s Pontból) nem lehet elindulni a modellezéssel, ahogy erre korábban már mások is rájöttek. De az sem lehet igaz, hogy a kiinduláshoz az egyenest (1D) és a kört (2D) kell használni. Szerintem a megoldás inkább a kettő keveréke lehet: az egységnyi (kvázi 0D-s) Pontból kell elindulni, ami felfogható protoegyenesként is, mivel még nem 1D-s, mert csak két pontból áll. Ez a két valódi nulla méretű Pont közti kvázi nulla távolság lesz az az alapegység, ami az egy létező Pont átmérőjének feleltethető meg.
Bár ezen okfejtéssel a modellezés elejére értünk (ami egyben a vége is), aminél tovább tényleg nem lehet jutni, senkit ne fogjon el az aggodalom a továbbiak miatt. Tisztázásra váró kérdések ugyanis még bőven maradnak a teremtésfilozófiában, és nem csak olyanok, amikre az Isten sem tudja a választ. Lássuk most a témához szorosan kötődő következményt, az időhullámok hatásmechanizmusának vizsgálatát.

3. A TASZÍTÁSI VEKTOROK HATÁSA

Az időhullámok a terjedésük során minden elért időforrást sodorni kezdenek, sugárirányban eltolva őket a normálisukra fektetett taszítási vektor irányának megfelelően. Egy hullámréteg egy jelenpontot a vastagságától függetlenül mindig csak annyival sodor a vektornyíl irányában (normálisan), amennyivel ő maga terjed, tehát E-vel. Vagyis a sodrásnak nincs erőssége, mert a transzcendens létezőnek (Pont) nincs ellenállása, amivel visszahatna erre az erőre (lásd: nincs erő ellenerő nélkül). Ebből következik, hogy egy jelenpont nem szakadhat el a vele érintkező hullámfronttól, vagyis az okforrások nem léphetnek ki az őskáosz vizéből. Csak a létezés vizeinek peremére juthatnak ki, annál tovább nem.
Ha több időhullám éri el egyszerre a Pontot, akkor a vektornyilak egyszerűen összeadódnak az ismert matematikai szabályoknak megfelelően (amik az idő geometriájából következnek). Az így kapott eredő mozgásvektor lesz egy jelenpont mozgása az eseménytérben. Mindaddig, amíg csak az őskáosz létezik, benne az okforrásokkal, a helyzet egyszerű és átlátható. De mi történik az első időhurok születésekor? Hogy fognak mozogni a taszítási vektorok hatására a különféle időhurkok az egyre komplexebbé váló hullámtérben?
Az időhurkok szerkezeti okokból lassabban mozognak az időhullámok terjedési sebességénél (RV<1). Ez esetben a hullámok mindig átszaladnak rajtuk, a mozgási paraméterektől függő időtartam alatt. Egy taszítási vektor annyi ideig sodorja az időhurok egy jelenpontját, amíg áthalad rajta, ezért az okforrások folytonos időtere egyenletes sodrású az időhurkokra nézve. Mindaddig, amíg a forrás sebessége és iránya változatlan. Azt viszont tudjuk, hogy az őskáoszban az okforrások sebessége lassan, de biztosan változik a taszítási vektorok eredő irányának finom módosulásai miatt, még akkor is, ha a haladási irányuk változatlan. Tehát az idősemmi hatása a teremtményekre abszolút értelemben egy folyamatosan változó és önmagát nem ismétlő befolyás, ami azok mozgását szintén egyedivé teszi.
A téridő hullámterében nem ilyen egyszerű a helyzet. Az időhurkokat alkotó jelenpontok (tachionok) ugyanis nem folyamatosan léteznek, hanem ciklusonként újrakeletkeznek új helyeken, majd megszűnnek. Emiatt az időhurkok hullámtere hiányos lesz. Tele lesz térhézagokkal, változatos méretű üres tartományokkal. Emellett a tachionok keringése okán a pozitív és negatív időrétegek összekeverednek, vagyis a taszítási vektorok iránya folyamatosan változik, meglehetősen bonyolult módon (4. ábra). Az időhurkok állandó kavarásának köszönhetően tehát a hullámterükbe kerülő jelenpontok őrülten bonyolult táncba kezdenek, n dimenziós szitálást végezve egész létezésük során. Ez a perturbáció a háttérzaj, egyben az információ átadódásának és megőrződésének, valamint elzajosodásának oka.


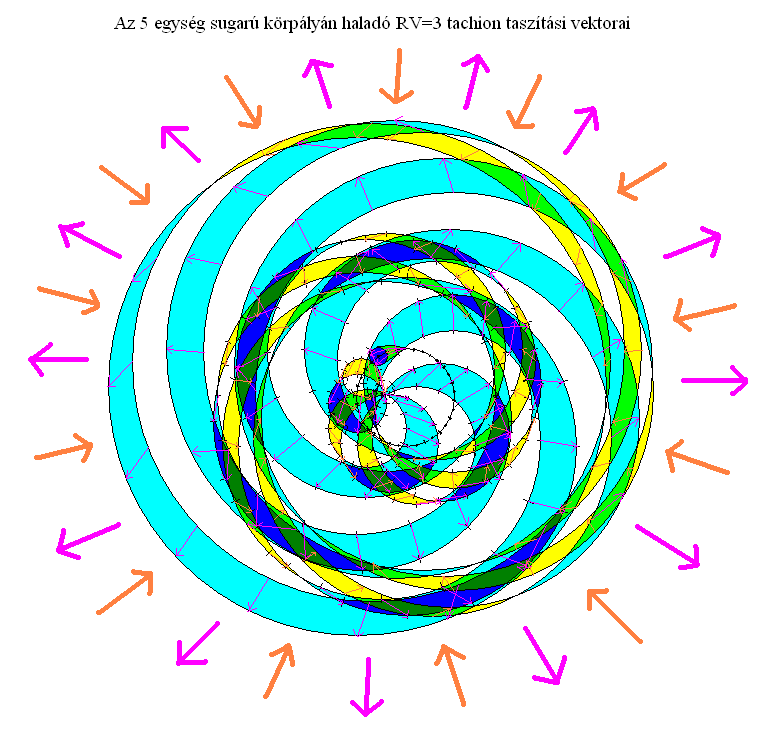
Mivel az időhurokban körpályán szaladó tachionok hullámtere csavarodó, ezért a taszítási vektorok nem pontosan a spirálgömb közepének normálisára esnek, hanem az időhurok körpályájának egyes pontjaira. Ezért kisebb-nagyobb szögeket zárnak be a középponti normálissal (aminek a legkisebb értéke nulla), amit tangenciális vektorral ábrázolhatunk. Ezt a hatást nevezzük érintőirányú sodrásnak, ami fizikailag nem egy önálló, külön taszítási vektor, hanem csupán a normális vektorok ciklikus elhajlása.
A fentiekből következik, hogy az őskáoszban (nemtér-nemidőben) a hullámtér taszítása kvázi egyenletes, vagyis szitálásra csak a téridőben kényszerülnek az időhurkok. Így az idősemmibe kiugró látogatót (szerinót) teljes nyugalom fogadja, ami azonnal csillapítóan hat a forrásainak mozgására és csökkenti a perturbációt, letisztítva annak belső információs terét. A hétköznapi életben ez a folyamat hasonló a meditációhoz, amikor valaki lecsendesíti és kiüríti az elméjét, hogy a saját belső ürességébe visszahúzódva pihenhessen.
Ha a téridőbe belép egy okforrás, akkor az is rögtön reszketni fog tőle (az Isten jelenlététől), ide-oda rángatózva a komplextérben. Az időhurkoknak annyiból jobb dolguk van egy okforrásnál, hogy a saját hullámterük behúzási tartománya miatt bizonyos korlátok között folyamatosan ellenállnak a mozgatóerőnek. Csökkenteni igyekeznek önnön deformációjukat, vagyis mintegy ellenerőt generálnak az őket érő erők hatására. Így megjelenik az időhurkok kölcsönhatásaiban az erő, aminek mozgatóképességét (munkavégzését) nevezzük a fogalom legáltalánosabb értelmében energiának. Az időhurkok ebből fakadó mozgási tehetetlensége lesz az oka az anyagi részecskék időtartályainál megfigyelhető tömegtehetetlenségnek, ami tehát nem más, mint a rendszerben eleve meglévő erőhatás.
Egy okforrásnak természetesen nincs tehetetlensége (nem ellenálló), így speciális (szinguláris) létezőnek kell tekintenünk, ami erőkifejtés nélkül mozgatható, és erőkifejtés nélkül képes bármit mozgatni (gyengén, de határozottan). Ezen erőtlensége miatt képes gyorsabban mozogni az időhullámok terjedési sebességénél, ami megfelelő körülmények között az összes vizek határára kisodorhatja, holtponti állapotba. Az időhurkok sosem juthatnak ki a vizek határára, így amíg csak léteznek, élő pontrendszernek kell őket tekintenünk, az időhurkok összességét pedig élő ponthalmaznak, azaz egyetlen élőlénynek.

Készült: 2008.05.07. - 09.

Következő írás

Vissza a tartalomhoz