A taszítási vektor az időhullámrétegek időforrásokra gyakorolt sodró hatásának irányát és nagyságát mutatja, ami alapján a jelenpontok elmozdulása számolható (14. ábra). Bár taszítási vektorból csak egyféle létezik, a normális (sugárirányú) vektor, az időhurkok kapcsán mégis beszélünk egy érintőleges (tangenciális) vektor komponensről is. Ami nem igazi, önálló fizikai vektor, hanem csak egy eredő elmozdulás oldalirányba a spirálgömbi térrétegek menetemelkedése miatt. Bár nagyságát tekintve sokkal kisebb a normálvektornál, mégsem elhanyagolható a hatása, különösen kis távolságokon, ahol a nagy görbület miatt képes erőteljesen beleszólni a jelenpontok pályagörbéinek alakulásába.
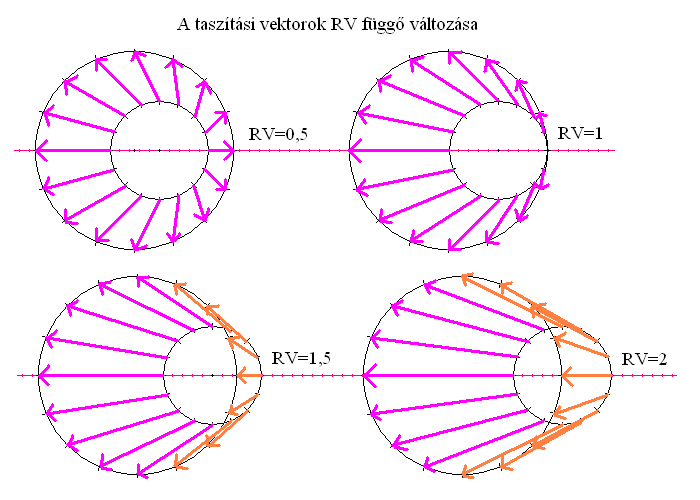
A normálist geometriailag vektornyíllal ábrázoljuk, ami mindig párhuzamos az adott hullámréteg sugárvonalával, vagyis ráfekszik az origóját a gömbfelszínnel összekötő szakaszra. A pozitív időrétegek vektorainak sodrási iránya kifelé (az origótól elfelé), a negatív időrétegeké befelé mutató (az origó irányába). A tardion sebességen haladó (RV<=1) jelenpontok hullámterében csak pozitív rétegek vannak, a tachion sebességűekében (RV>1) pedig pozitív és negatív rétegek is, amik egymást átfedve kettős idősűrűségű időközeget hoznak létre. Negatív rétegek önmagukban (pozitívak nélkül) nem jöhetnek létre geometriai okokból.
A normálvektorok nagysága, azaz hossza matematikailag megegyezik egy időréteg vastagságával, de fizikailag egy taszítási vektor mindig csak egységnyi (E=1) sebességgel sodorja az elért időforrásokat. Éppen ezért szigorúan különbséget kell tenni a matematikai és fizikai vektor között, mert a jelenpont fizikai elmozdulását csak a fizikai vektorok összegzésével lehet meghatározni. Abban az esetben viszont, ha az időréteg átszalad az időforráson (időhurok esetén), fontos ismerni a matematikai vektor hosszát is, mert ennek mérete határozza meg azt az időtartamot, amelyen keresztül a fizikai vektor kifejti taszító hatását. Az ezzel kapcsolatos számítások metódusait még kutatni kell, mert a téma egyelőre nincs kielégítő pontossággal tisztázva.
A téridő hullámrétegeinek taszítási vektorai különféle szögeket zárnak be egymással, nem csupán a különböző helyeken, de egymást átfedve is (15. ábra). Mivel a hullámrétegek forrása köríven mozog, az időhuroknak két origója is van. Az egyik a hurok középpontja, ami nem feltétlenül esik egybe a szívponttal és virtuális origónak tekintjük. A másik a körpályán haladó tachion aktuális jelenpontja, ahonnan az adott időréteg kiáradt (származik) és valós origónak tekintjük. A téresszencia felszínén a két origóból húzott sugárvonalak vagy szöget zárnak be egymással vagy párhuzamosak (mert egymásra esnek). Tehát a kétszeres (vagy többszörös) idősűrűségű téresszenciákban az egymást átfedő réteghullámok vektorai a sugárvonalak által bezárt szögeknek megfelelően állnak, kifelé vagy befelé mutatva. Ez a szög a távolsággal exponenciálisan csökken, de csak a végtelenben éri el a nullát, vagyis valamekkora oldalirányú elsodró hatást mindig okoz a jelenpontok számára. Ezért nevezzük érintőleges vektornak.
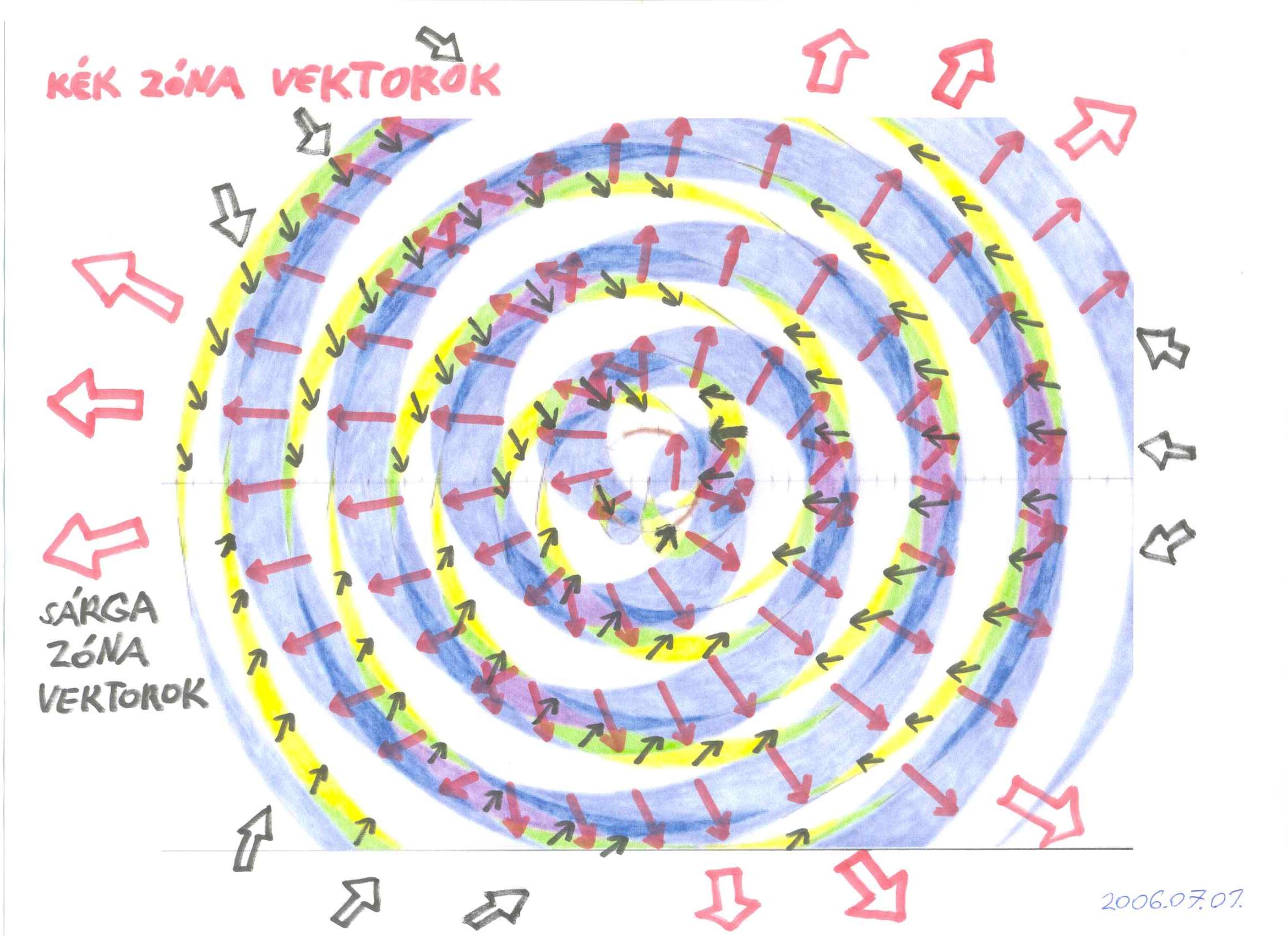
A taszítási vektorok határozzák meg a téridőben található összes jelenpont mozgásának eredő irányát, és egyben felelősek magáért a mozgásért (és deformációért), ami az időhullámok sodró hatásának következménye. Minden mozgás időben történik, aminek egy leképzése, praktikus ábrázolása a térbeli elmozdulás. A térbeli kiterjedés (térdimenzió) tehát az időhullámtérben végzett időbeli áthelyeződések függvénye. Vagyis időtlen tér, mint olyan, nem létezik. Teretlen idődimenzió viszont létezik, a téridőn kívül az őskáoszban (ezért nevezzük idősemminek).
Egy pozitív vagy negatív téresszencia réteg (ami több időhullámrétegből áll a folytonos modellben) többnyire sokkal vastagabb, mint amekkora egy időforrás átmérője (ami nulla), és lehet kisebb vagy nagyobb, mint egy időhurok (szerinó, fotinó) átmérője (16. ábra). Így biztosan kijelenthetjük, hogy egy időréteg vastagsága szinte mindig meghaladja három egymás mellé helyezett, minimálegyenest alkotó pont hosszát, vagyis térbeli kiterjedése van. Ennélfogva a jelenponton áthaladó téresszencia hatása nem időpontszerű, hanem időszálszerű (szakaszos), vagyis van ideje hatást kifejteni rá (mozgatni). A jelenpontok pedig mindig arra mozognak, amerre a rajtuk áthaladó időhullámok vektorai eredően taszítják őket. Ennek a térdimenzió megjelenése kapcsán van nagy jelentősége, amivel egy későbbi fejezetben részletesen is foglalkozunk.
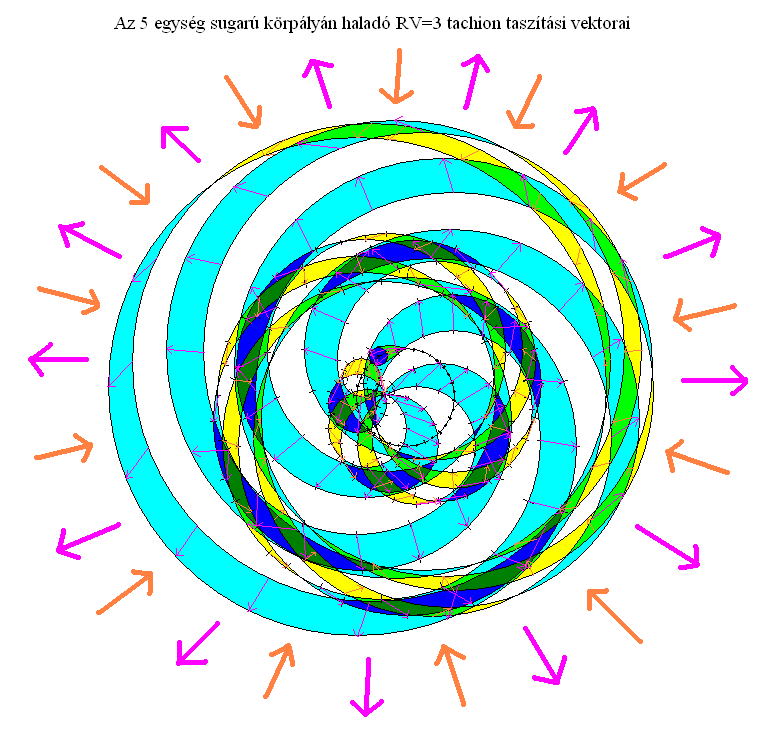
A diszkrét ábrázolásnál jól megfigyelhető, hogy a balról jobbra, tehát órairányban keringő tachion múltszféráinak tágulása bentről kifelé haladva két egymással ellentétes irányú csavarodást végez. A pozitív időrétegek és a csöndzóna szintén órairányú, a negatív rétegeké pedig azzal ellentétes. A pozitív téresszenciák úgy taszítanak kifelé, hogy közben az időhurok virtuális origójából nézve a vektoraik időnként balra dőlnek a sugárvonalhoz képest, tehát az órairánnyal ellentétesen sodornak oldalra, míg a negatív téresszenciák úgy vonzanak befelé, hogy közben a vektoraik időnként jobbra dőlnek, vagyis órairányban sodornak oldalra. A negatív sodrás a maximumát ott éri el, ahol rétegei metszik a csöndzónát.
A folytonos ábrázolásnál hasonló a helyzet, de ott nincs csöndzóna. Helyette a negatív sodrás a térhézagokban éri el a maximumát. A kettős idősűrűségű tartományokban a pozitív és negatív vektorok által bezárt szögek pedig – a paraméterezéstől függően – feltűnően nagyok lesznek, ahogy a kettős pozitív vektorok szögei is.
A téresszenciák taszítási vektorainak időforrásokra gyakorolt hatása eredményezi többek között a szeparációs hatást is, aminek következtében a párhuzamos térszeletek gyakorlatilag teljesen el vannak szigetelve egymástól. Bár ezt a jelenséget szeparátornak nevezzük, a kifejezés alatt nem valamilyen falat vagy szigetelő réteget értünk, hanem egy folyamatos elsodró hatást, ami megakadályozza, hogy az egyes térszeletekben tartózkodó teremtmények csak úgy, spontán átkerülhessenek a szomszédos terekbe, illetve kisodródjanak a nemtér-nemidő rétegbe.
7. fejezet
Vissza a tartalomhoz