A fizikai térdimenzió a téridő hullámterében végezhető, egymásra merőleges elmozdulások lehetőségének a kifejeződése. Ezen elmozdulások irányai a hullámtér aktuális taszítási vektorai által határozódnak meg, amiben a teremtmények időhurkai léteznek és mozognak. A hullámtér szeparációs, kényszerítő ereje (hatása) folytán a belekerülő időhurkok pályagörbéi csak azon irányokba terjedhetnek ki, illetve csak arrafelé mozoghatnak, amelyeket a beágyazási környezet megenged a számukra.
A taszítási vektorok irányai pedig alapvetően a térszerán tachionjának mozgáspályájától függenek. Attól, hogy hány térdimenzióban mozog egy ciklusidő alatt a tachion jelenpontja a körív mentén. Ez alapból 3D-s, de mivel a főszerán az őskáoszban tetszés szerint elfordulhat n+1 idődimenzióban is önmagához képest, az alfatér önkorlátozás nélkül 4D-s téresszenciákból fog állni (monász szerinó esetén).
Ahhoz, hogy megérthessük a térdimenziókat, vissza kell térnünk az időfizika alapjaihoz, a jelenpontok megnyilvánulásához és relatív mozgásához az őskáoszban. Kezdjük azzal, hogy az időforrás forgása a saját tengelye körül csak időbeli mozgás, nem térbeli, aminek két oka van. Az egyik, hogy a forgás minimális térdimenziószáma azonos a forgó objektum kiterjedésével (0D-s). A másik, hogy a forma és szerkezet nélküli pont (elemi létező) kinézete nem változik a forgás közben, ezért térbeli alakváltozásról, deformációról sem beszélhetünk. Ugyanígy az időhullámok skaláris (valójában egy idődimenziós) kiáradása sem tekinthető térbeli mozgásnak, mert a gömbhullám teljesen forgásszimmetrikus minden tengelyre nézve, így tulajdonságában egyenértékű a forrásával.
Ezért nem beszélhetünk fizikai térdimenzióról az őskáosz hullámterében, csak egy idődimenziós kiterjedésről (ősidő), aminek belső geometriai szerkezetét (tardionok, tachionok hullámterét) megkülönböztetésül eseménytérnek nevezzük. Az idősemmiben minden létező okforrás (Bindu) ősideje egy önálló idődimenziót alkot, ezért a tíz okforrás együtt egy tíz idődimenziós kiterjedést kelt.
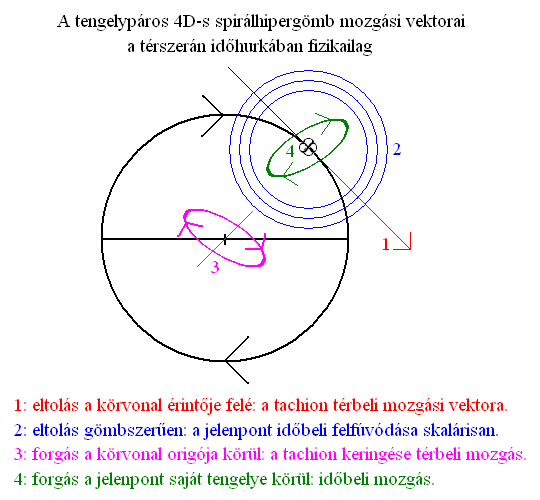
Ezzel szemben az időforrás keringése az időhurokban, egy külső tengely körül már térbeli mozgás, mivel a körpálya minimális térdimenziószáma 2D. Tehát a körív mentén haladó tachion egyrészt forog a saját tengelye körül, másrészt kering az időhurok virtuális origója körül. Továbbá szalad a körív mentén előre és kiárad a sajátideje minden irányban skalárisan (ami plusz egy önálló idődimenziót jelent). Ha ezen mozgásokat összeadjuk, akkor két időbeli és két térbeli mozgás együtt alkotja a téridő hullámterének 4D-s kiterjedését, ahogy az a tér matematikai szerkezetét leíró modellekből egyértelműen kiderül (17. ábra). Két forgás és két egyenes vonalú mozgás együtt egy 4D-s spirálgömböt eredményez. Ezzel megteremtettük a logikai kapcsolatot a tér fizikai és matematikai leírásai között, ami a későbbiekben hasznos segítség lesz a további térszerkezeti kutatások és technológiai fejlesztések számára. Az elszántabb mérnökök máris elkezdhetik dörzsölni a kezüket, mert nagyon izgalmas felfedezéseket tehetnek majd az itt leírt alapelvek ismeretében.
Ahogy azt már kifejtettük, egy téresszencia térdimenziószáma attól függ, hogy a hullámrétegek taszítási vektorai milyen szögeket zárnak be egymással. Monász szerinónál ez 3D-s vagy 4D-s térszeleteket eredményez a mozgásától függően. Mivel a vektornyilak által bezárt szögek abból adódnak, hogy az időhurokban keringő tachion mozgásának mekkora az eseménytérbeli kiterjedése, logikusan következik, hogy a szerinótól távolodva a szögek mértéke folyamatosan csökken, ahogy a felfúvódó időgömb egységnyi felületre (2D) vagy térfogatra (3D) eső görbültsége csökken. Vagyis a térhullámok egyre inkább egyenes felszínűnek tűnnek a szemlélők számára.
A vektorok által bezárt szög csökkenése elvileg a térdimenziószám csökkenéséhez kellene, hogy vezessen. Erre mondjuk azt, hogy egy idő után ellaposodnak a dolgok. De mivel mi nem most jöttünk a falvédőről (síkuniverzumból), már elég bölcsek vagyunk hozzá, hogy észrevegyük, a gyakorlatban mégsem történik ilyesmi. Tehát az Istentől nagyobb távolságra lévő (vagy elkódorgó) teremtményeknek sem kell a fokozatos kilapulástól tartaniuk. A téridőben a térszerán körül lebzselő különféle teremtmények ugyanis mind kiárasztják a saját hullámterüket, ami szintén annyi térdimenziós, mint a helytartóé. Ezek hatása mintegy kiegészíti a térszeletét, afféle pót-térerősítőként, vagyis a beágyazott időhurkok egymást tartják megfelelő kiterjedési állapotban.
A dolog azonban mégsem ennyire egyszerű. A főszerán saját mozgása ugyanis az őskáoszban a téridő szerkezetének modulációjával, eltorzulásaival jár. Ez pedig nem mindig tesz jót az érzékenyebb felépítésű teremtményeknek. Emiatt veszi körbe magát az Isten kerubokkal (az Úr körül álló angyalokkal), akik térerősítőként és téringadozás kiegyenlítő bétatéri szerinóként, azaz lokális helytartóként működnek az univerzumban. A témával korábban már részletesen foglalkoztunk az angyali hierarchia működése kapcsán, és fogunk is még vele foglalkozni külön írásokban.
A klasszikus fizikában már régen megjelentek a magasabb térdimenziókkal kapcsolatos elméleti vélekedések, de gyakorlati eredményeket, méréseket még senki sem tudott produkálni. Pont azért, mert magával a téridő szerkezetével nem voltak tisztában a kutatók. Ettől függetlenül szépen elnevezték a 4D-s túlteret hipertérnek (a két szó ugyanazt jelenti, csak mi jobb szeretjük a magyar kifejezéseket, mivel sokatmondóbbak), és még a benne lehetséges mozgásirányoknak is neveket adtak. Ezek a következők:
1D: hosszúság: előre-hátra.
2D: szélesség: balra-jobbra.
3D: magasság: fel-le.
4D: túlhossz: ana-kata.
Az ana-katát magyarul inkább anya-atyának kéne mondani, a két Teremtő iránti tiszteletből, és mert ennek több értelme van.
Az a tény, hogy az általunk ismert téridő többnyire megbízhatóan egyenletesnek mutatkozik, mintha egy szerkezet és változások nélküli puszta üresség lenne, csak azt mutatja, hogy a lokális fenntartók milyen jó munkát végeznek. Mindazon parajelenségek pedig, amikor különféle téranomáliák jelentkeznek a természetben, amiket a szemtanúk és a beszámolókat komolyan vevő kutatók nem tudnak megfelelően értelmezni, azt mutatják, hogy időnként hibák is előfordulnak a rendszerben (lásd: Bermuda-háromszög). Ezek súlyosabb esetben akár az egész bolygónkat is elpusztíthatják, körülbelül egyhuszad másodperc alatt. Méghozzá olyan tökéletesen, hogy por sem marad belőle, és észre sem vesszük, hogy már nem is létezünk. Az a tény azonban, hogy már jó ideje itt vagyunk, és értetlenül szemlélhetjük a világegyetem nagyszerűségét és sokszínűségét, ad némi reménykedésre okot a jövőt illetően. Végül is csak buta kisgyerekek vagyunk a nálunk nagyságrendekkel idősebb istenek civilizációjához képest, akik létrehozták és fenntartják ezt a Naprendszert, meg minden mást is körülöttünk, sok milliárd fényéves körzetben.
Az élethez rendre van szükség, ami ellenáll az entrópia zűrzavarának és összetartja a létrehozott különféle struktúrákat. Amint az látható, a téridő spirálgömbi hullámtere a bonyolult belső szerkezete, és ciklikus ismétlődése okán egyfajta dinamikus rendezettséget mutat. És ezt folyamatosan rákényszeríti a benne lévő (belekerülő) dolgokra. Azáltal, hogy a taszítási vektorai minden időforrást meghatározott irányú szitálásra kényszerítenek folyamatosan, és szeparációs viselkedésükkel megakadályozzák a másféle irányú elmozdulásokat. A téridő tehát lekorlátozza a 10 idődimenziós őskáosz rendszertelenségét egy 4 térdimenziós rendszerré (alapból), s benne emiatt válik értelmezhetővé a távolság, az irány, az időbeli egymásutániság és a késedelem, valamint a mozgás és deformáció, na és persze a sebesség, a gyorsulás, meg minden más, ami a világra jellemző. És pont ezért lehet a téridőből kilépve áthágni ezen lokális játékszabályokat, eredő természeti törvényeket, hogy térugrást vagy időcsúszást (érthetőbben: időutazást) végezzünk. Ahogyan a térugró hajtómű megvalósítható, úgy az időgép is elkészíthető és használható, de ezzel szintén a későbbi írásainkban foglalkozunk részletesen.
Visszatérve a térdimenziók tulajdonságaira, ha megnézzük a keringő tachion diszkrét ábrázolását, láthatjuk, hogy egy térhullámrétegben maximum három eseményhorizont réteg metszi egymást. Vagyis három taszítási vektor határozza meg az adott ponton található időforrás számára a lehetséges mozgásirányokat. Két pozitív taszítás kifelé, két különböző irányba, és egy negatív taszítás befelé, de egyik pozitívval sem párhuzamosan. Ha a tachion nem síkban, hanem térben kering, az eredmény egy 3D-s spirálgömbi hullámréteg. Ha a tachion pályagörbéjét kiforgatjuk a túltérbe, az egymást követő rétegek vektorai a 4D-ben fognak elmozdulni, már egy rétegen belül is. Vagyis egy térrétegbe egy négy szálú térkereszt illeszthető bele. Ennek a 4D-s hipergömbnek minden tetszőleges eseményhorizontja, azaz felszíne egy 3D-s térfogat (pontosabban térszín) lesz, az időmatematikai törvényeknek megfelelően.
Ahhoz, hogy a térszerán tachionjai megfelelő pályagörbe mentén keringjenek minden önkeltési ciklus során, a térforrás működését nagyon pontosan szabályozni kell, és védeni a külső zavaroktól (háttérzajtól), nehogy kiessen a szinkronizált mozgásból. Akár 3D-s, akár 4D-s térszeletek keltése a cél. Ezt a szabályozást az Isten a kerubjai segítségével végzi, akiken keresztül állandó visszacsatolást létesítve, az ő hullámtereikkel terelgeti a saját időhurkát a megkívánt irányokba. Itt elsősorban nem egyenes irányú helyváltoztató mozgásokról van szó, hanem különféle helyzetváltoztatásokról, vagyis forgásokról, keringésekről, csavarodásokról és tekergésekről.
10. fejezet
Vissza a tartalomhoz