A térszorzás a szerinó ciklikus önkeltési folyamatának olyan módosítása, speciálisan szabályozott csavarodások segítségével, amely miatt a forráshelyek száma megnő, miközben a források száma változatlan marad. A növekmény mindig egy térhatosnak felel meg, azaz a külső szemlélő számára az öt tachion és egy szívpont úgy mozog önmagához képest, mintha két állapot között ingázna oda-vissza, de egy helyen. Az új forráshelyek nem egy önkeltési cikluson belül jelennek meg az időhurokban, hanem egymással szinkronizáltan, időben egymás után, felváltva kerülnek bejárásra az időforrások részéről (18. ábra). Tehát a tachionok és a szívpont az egyik ciklusban az egyik térhatost foglalja el és kelti, a másikban a másikat, majd újra az elsőt. Felfogható a folyamat két pontrendszer oszcillációnak is.
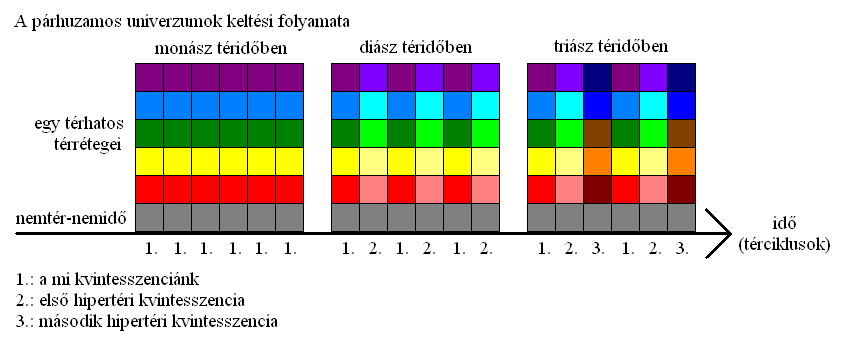
Így lesz a monász szerinóból (egy térhatosból) térszorzással diász szerinó (két térhatos), majd ebből további térszorzással triász szerinó (három térhatos). A mi téresszenciánkat keltő térhatost hívjuk egyszerűen téridőnek, a másik térhatost vagy térhatosokat pedig hipertereknek, amik a keltőjük és a bennük tartózkodók számára fizikailag teljesen egyenértékűek, és szerkezetileg egymásba ágyazottan, ugyanakkor elszeparálva, párhuzamosan léteznek. A térszorzás geometriai szabályai miatt természetesen más és más lesz a hullámtér szerkezete a térforrás körül, attól függően, hogy monászként, diászként vagy triászként működik (19. ábra).
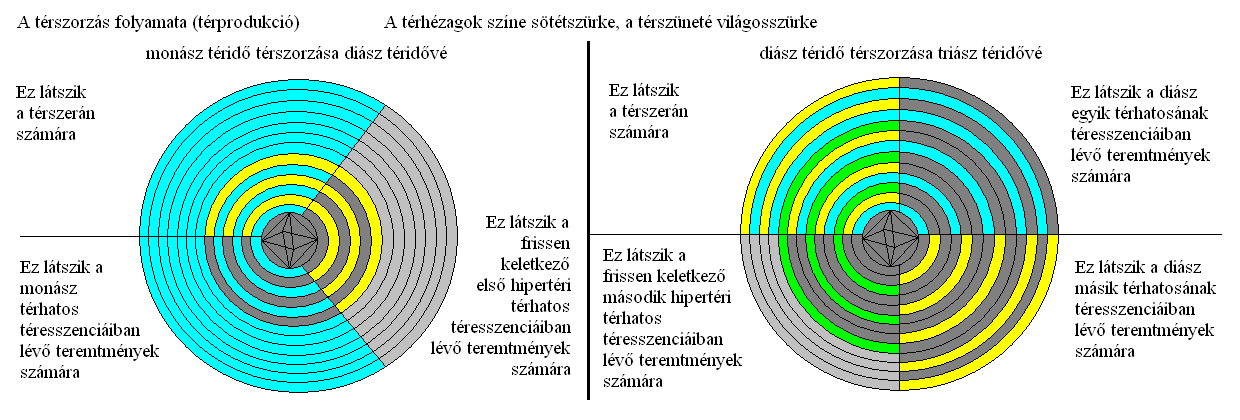
Mivel a térszorzás eredménye tartós is lehet, azaz sok ciklusidőn át megmaradhat, akár évmilliárdokon keresztül, nem tekintjük téringadozásnak, sem téranomáliának. Műveletileg pedig nem azonos a matematikai szorzással, mivel a szerinó csak egy, kettő vagy három térhatos keltésére képes. A térszorzás folyamatához a szerinónak mindenképpen harmadlagos csavarodásokat kell végeznie, ami térprodukciót jelent a gyakorlatban. Viszont nem minden térprodukció eredményez térszorzást. A térszorzás ráadásul csökkenti a térsűrűséget minden térszeletben, de nem a hullámrétegek vastagságának (a hullámhossznak) a növelésével, hanem a köztük megfigyelhető térhézagok vastagságának növelésével. Ugyanakkor nem jár feltétlenül együtt a térdimenziószám növekedésével az egyes térszeletekben, mert ez a térprodukciótól függő jelenség.
Fizikailag tehát a térszorzás folyamata úgy történik, hogy egy 3D-s monász szerinó harmadlagos csavarodásokat kezd el végezni, vagyis térprodukcióval 4D-s téresszenciákat kelt maga köré. Ha nem végez harmadlagos csavarodást, csak másodlagosakat, akkor a hullámtere mindössze 3D-s minden téresszenciában (ilyen a mi lokális téridőnk a Naprendszerben). A harmadlagos csavarodások speciális beállításával jön létre a forráshelyek megkettőződése és az első hipertéri térhatos megjelenése. Ekkor és emiatt a diász szerinó időhurkának pályagörbéje 4D-ssé válik, ami azt eredményezi, hogy a harmadlagos csavarodásai másodlagossá redukálódnak a számára.
A következő lépésben a diász szerinó ismét harmadlagos csavarodásokat kezd el végezni, vagyis térprodukcióval 5D-s téresszenciákat kelt maga köré. Ezek speciális beállításával jön létre a forráshelyek számának további növekedése és a második hipertéri térhatos megjelenése. Ekkor és emiatt a triász szerinó időhurkának pályagörbéje 5D-ssé válik, vagyis a harmadlagos csavarodásai ismét másodlagossá redukálódnak a számára. Ennek különlegessége, hogy ilyenkor az időhurokban minden tachion haladási vektora egy-egy térdimenzió irányába mutat. Többek között ennek is köszönhető, hogy a további növekedés leáll, mert nincs több jelenpont a 6D-ssé bővítéshez (lásd a minimálgömbök időmatematikáját A három pont tétel című írásban). Azt még megteheti a triász szerinó, hogy harmadlagos csavarodásokat végezve 6D-s téresszenciákat keltsen maga köré, de semmi többet.
Elméletileg elképzelhető lenne, hogy tovább folytatva a térszorzást, egyre több párhuzamos térhatost hozzunk létre a meglévő rendszerből, tetrászt, pentászt, stb. képezve. A gyakorlatban azonban ez nem lehetséges, mivel az időhurok önkeltési folyamatát meghatározó hullámtér oly mértékben változik meg, hogy akadályozni kezdi a térszorzáshoz szükséges csavarodó mozgásokat. Így a téridő maximum triász típusú lehet, vagyis limitált a bonyolultsága és a térdimenziószáma. Ettől függetlenül azonban fizikailag lehetséges, hogy komplex anyagi rendszereket, például elemi részecskéket, atomokat (tárgyakat) olyan bonyolult pályákon mozgassunk, egyszerre több tengely körül, ami matematikailag megfelel ezeknek a műveleteknek. A témával később külön írásokban foglalkozunk még.
Kiegészítés: A térszorzás fogalmával az időfizikai kutatásaim során először az akashában böngészve találkoztam, egy ősi mezopotámiai agyagtáblán lévő tudományos szöveget olvasva, amiben a Földre sok ezer éve betelepült őseink által ránk hagyott időfizikai tudás egyes elemei szerepeltek. Ebben a hun nyelvű leírásban a térforrás működésével kapcsolatban került említésre a téma, aminek megértése fontos a térugrásos űrhajózáshoz.
Később Maurits Cornelis Escher, múlt századi holland grafikus képein sikerült fölfedeznem a térszorzás geometriai ábrázolását mind a szerinó, mind a fotinó esetében. Az alkotó egyik közismert grafikáján (Vízesés: 20. ábra) jól látható mindkét energiakvantum felszorzott változata. A két torony tetején lévő testekről van szó, ahol a bal oldali, három egymásba rakott kocka felel meg a fényszorzással létrejövő triád fotinónak, a jobb oldali, három egymásba rakott oktaéder pedig a térszorzással létrejövő triász szerinónak. Escher időfizikai kutatásainak elemzésével később külön írásban foglalkozunk még.

13. fejezet
Vissza a tartalomhoz