A térszorzás ellenkezője a térosztás, a térhatosok számának csökkentése (21. ábra). Ilyenkor a megszűnő térhatos helyén térszünet marad vissza, azaz a téresszenciák eltűnnek és egy üres hiányzóna terjed ki a forrásrendszerből, ami gyakorlatilag megfelel a nemtér-nemidőnek. Így lesz a triász szerinóból (három térhatosból) térosztással diász szerinó (két térhatos), majd ebből további térosztással monász szerinó (egy térhatos).
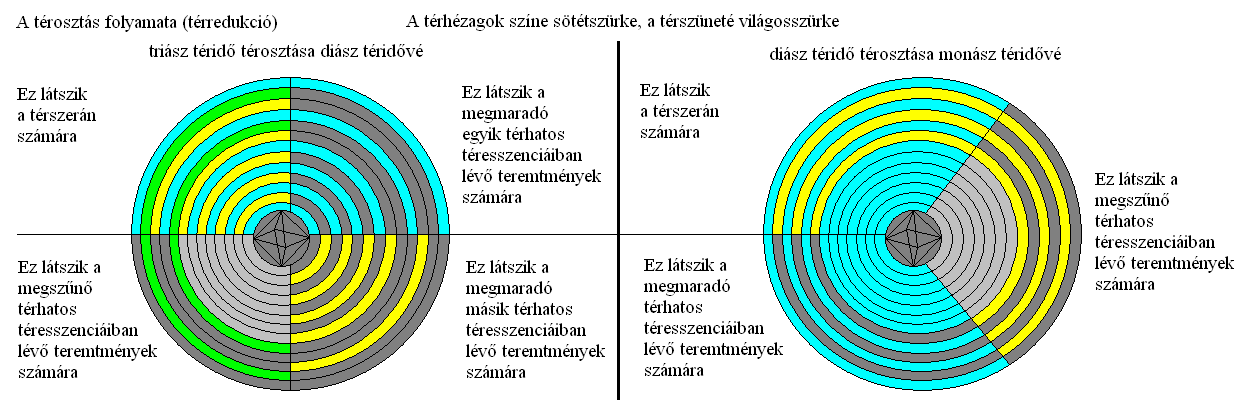
A térosztás értelemszerűen növeli a térsűrűséget minden térszeletben, de nem a hullámrétegek vastagságának (a hullámhossznak) a csökkentésével, hanem a köztük megfigyelhető térhézagok vastagságának csökkentésével. Ugyanakkor nem jár feltétlenül együtt a térdimenziószám csökkenésével az egyes térszeletekben, mert ez a térredukciótól függő jelenség.
Fizikailag tehát a térosztás folyamata úgy történik, hogy egy 5D-s triász szerinó abbahagyja a harmadlagos csavarodásokat, vagyis térredukcióval 5D-s téresszenciákat kelt maga köré a korábbi 6D-sek helyett. Ezután a másodlagos csavarodásait redukálja úgy, hogy az időhurok tachionjainak pályagörbéje csak 4D-s legyen, mire a három térhatosból valamelyik, amelyiket előre kiválasztott, kiesik a mozgási útvonalából és csak kettő marad. Ekkor 4D-s diász szerinóként ismét végez harmadlagos csavarodásokat, amikkel 5D-s téresszenciákat kelt. A következő lépésben a diász szerinó megint abbahagyja a harmadlagos csavarodásokat, vagyis térredukcióval 4D-s téresszenciákat kelt maga köré. Ezután a másodlagos csavarodásait redukálja úgy, hogy az időhurok tachionjainak pályagörbéje csak 3D-s legyen, mire a két térhatosból valamelyik, amelyiket előre kiválasztott, kiesik a mozgási útvonalából és csak az egyik marad. Ekkor 3D-s monász szerinóként ismét végez harmadlagos csavarodásokat, amikkel 4D-s téresszenciákat kelt. Ezek tovább redukálhatók a harmadlagos csavarodások abbahagyásával 3D-ssé, de tovább lefelé nem (22. ábra). A 2D-s térszeletek keltése más módszerekkel történik, amivel később külön írásban foglalkozunk még.

A szerinó síkvetületi képe a hatágú tércsillag, ha a forráshelyeket ábrázoljuk, illetve az ötágú tércsillag (pentagramma), ha az időforrásokat ábrázoljuk. A hatágú tércsillagnak van egy általánosan elterjedt változata, az utóbbi évszázadokban Dávid-csillagnak (Dávid pajzsa) nevezett szimbólum, ami két egyenlő oldalú, szimmetrikusan egymáson fekvő háromszögből áll. Ez az oktaéder síkvetületi képe, a hatszög oldalai nélkül. A szerinónak emellett létezik még egy 1D-s szakasszá kihúzott változata is, amit a hat plusz egy ágú gyertyatartó (térmenóra) szimbolizál. Ennek működésével korábban már foglalkoztunk.
14. fejezet
Vissza a tartalomhoz